1、单线性插值

单线性插值是一种用于估计两个已知数据点之间未知点的方法。它基于线性关系，通过计算目标位置的值，使用已知点之间的线性函数进行插值。这在图像处理中常用于放缩、旋转等操作，计算简单，产生平滑结果，但在放大时可能造成轻微模糊。

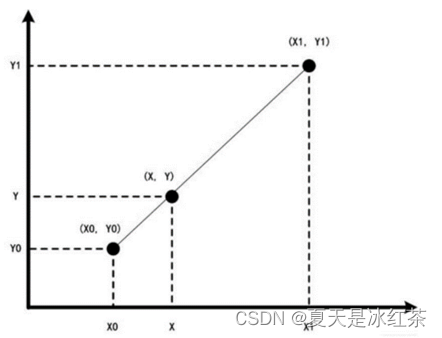
目前已经知道了与之间的斜率，在这个区间内，我们要求某x对应的y值很容易，因为它是线性的，那么通过与两点的斜率，以及与之间的斜率，即可假设出直线方程。

通过计算就能算出x点对应的函数值y了

2、双线性插值

双线性插值是一种用于估计两个已知数据点之间未知点的方法。它考虑了目标位置在两个方向上的线性关系，通过对四个最近的已知点进行加权平均，进行插值计算。这在图像处理中常用于平滑放缩、旋转等操作，比最近邻法更精确，产生更平滑的结果。

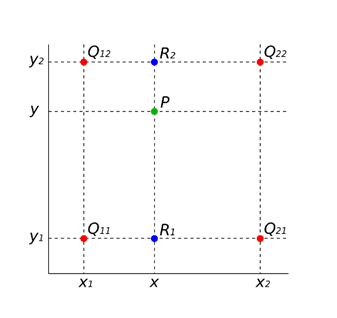
如图所示，我们需要求P点的像素值。我们已知了Q11、Q21、Q12、Q22、P的坐标。也知道Q11、Q21、Q12、Q22的像素值。所以先用关于X的单线性插值去分别计算R1、R2的像素值。

在右边的等式中的字母f(Q11)、f(Q12)、f(Q21)、f(Q22)、x1、x2、x都是已知的，求出的f(x,y1)与f(x,y2）即为R1、R2的像素值。

再使用关于y方向的单线性插值计算P点的像素值

得出：

在右边的等式中的字母y1、y2、y都是已知的，与即为上一个式子中求出的R1、R2像素值。

3、手写代码实现

代码显示参考的这位博主的。双线性插值法（Bilinear Interpolation）_绯雨千叶的博客-CSDN博客

但它使用的是显示循环，对于计算量较高，这里我对代码进行了改进，采用了网格坐标、数组广播和矩阵运算等技巧，使得插值过程更加高效。 

import cv2
import numpy as np
import pyzjr as pz

# 已添加进pyzjr中
def bilinear_interpolation(image, scale):
    ah, aw, channel = image.shape
    bh, bw = int(ah * scale), int(aw * scale)
    dst_img = np.zeros((bh, bw, channel), np.uint8)

    y_coords, x_coords = np.meshgrid(np.arange(bh), np.arange(bw), indexing='ij')
    AX = (x_coords + 0.5) / scale - 0.5   # 移向像素中心
    AY = (y_coords + 0.5) / scale - 0.5

    x1 = np.floor(AX).astype(int)
    y1 = np.floor(AY).astype(int)
    x2 = np.minimum(x1 + 1, aw - 1)
    y2 = np.minimum(y1 + 1, ah - 1)
    R1 = ((x2 - AX)[:, :, np.newaxis] * image[y1, x1]).astype(float) + (
                (AX - x1)[:, :, np.newaxis] * image[y1, x2]).astype(float)
    R2 = ((x2 - AX)[:, :, np.newaxis] * image[y2, x1]).astype(float) + (
                (AX - x1)[:, :, np.newaxis] * image[y2, x2]).astype(float)

    dst_img = (y2 - AY)[:, :, np.newaxis] * R1 + (AY - y1)[:, :, np.newaxis] * R2

    return dst_img.astype(np.uint8)

image=cv2.imread(r"./data\campuscrack\00231.jpg")
dst_img=bilinear_interpolation(image,1.5)
cv2.imshow("name2",image)
cv2.imshow("name",dst_img)
cv2.waitKey(0)

scale=1.5的效果: 

4、实验分析

     双线性插值在图像处理中的意义是通过在两个方向上的插值，更准确地估计新像素的值，以改善图像的质量、平滑边缘，并保持细节，从而实现图像放大、缩小、旋转等操作的高质量效果。