北邮22信通：第五章 图 最短路径 Dijkstra算法

news2024/9/25 3:19:11

 北邮22信通一枚~   

跟随课程进度每周更新数据结构与算法的代码和文章 

持续关注作者  解锁更多邮苑信通专属代码~

获取更多文章  请访问专栏：

北邮22信通_青山如墨雨如画的博客-CSDN博客

一. 算法核心思想

        Dijkstra算法是用来求取图中两个结点之间最短路径的算法。已知一个始发结点，如何求取到某节点的最短路径呢？

        Dijkstra算法给出了这样的思想：加法原则。先取最少量事件，一次加入一个事件，直到所有事件被加入进去为止。对某一次加入的事件：如果事件加入后能够优化上一次的结果，那么更新结果为被优化的结果，否则保持原样不动。

具体过程如下（书上给出的过程+小编批注）：

（1）找出从源点能够直接到达的顶点的所有路径，并从中选出一条最短路径；

（2）以这条已选出的最短路径作为转发路径/*批注：先取最少量事件*/，找出经过这条路径转发后到达其他顶点的路径，从中选出一条最短的路径；需要注意的是，如果这条路径转发后到达目的结点比直接从源点到达目的结点的结点路径长，就不用转发了；

/*批注：看加入的事件能否优化原先的结果，有优化则优化，不能优化保持原样；*/

/*又批注：这里需要有一个函数，能够找出这条最短路径。*/

/*又批注：这里需要一个辅助数组（path），数据类型为整型，长度为结点个数，用来记录源顶点到顶点i的路径。这个数组是最妙的，我们放在“测试”部分讲解。*/

（3）重复执行（2），直到找到所有顶点的路径位置。/*批注：需要一个辅助数组，数据类型为布尔型，长度为结点个数，用来记录某个顶点是否被添加*/

实际上步骤二是一个迭代算法，具体过程如下：

（1）记录所有直接与源点相连的顶点的路径，找出其中与源点最近的顶点vi，在辅助数组中将其标注为已经被用过；

（2）将vi作为转发结点，重新计算从v经过vi可以到达的顶点路径disk[ 1…n ]，对于任意结点j，若经过vi转发后的路径disk[ j ]小于之前的路径长度，则更新disk[ j ]，否则保留原来的值，更新完毕后，找出disk[ 1…n ]中路径最短的顶点，在辅助数组中将其标注为已经被用过；

（3）重复执行（2）每次都将上次新标记的顶点作为转发结点，重新计算disk[ 1…n ]的值，直到最后一个顶点被标记，算法结束。

二.几点说明

2.1存储结构

本篇文章采用邻接矩阵作为存储结构来实现算法。

#include<iostream>
#include<fstream>
#include<queue>
using namespace std;

class student
{
private:
	int ID;
	string name;
public:
	student()
	{
		this->ID = 0;
		this->name = "un_known name";
	}
	student(int ID, string name)
	{
		this->ID = ID;
		this->name = name;
	}
	void print()
	{
		cout << "ID:" << this->ID << "  name:" << this->name << endl;
	}
	friend fstream& operator>>(fstream& fin, student& s)
	{
		fin >> s.ID;
		fin >> s.name;
		return fin;
	}
};

const int maxsize = 10;
template<class temp>
class m_graph
{
private:
	temp vertex[maxsize];
	int arc[maxsize][maxsize];
	int vnum, arcnum;
public:
	m_graph(ifstream& fin);
	m_graph(temp a[], int arc[][maxsize], int vnum, int arcnum);
};

template<class temp>
m_graph<temp>::m_graph(ifstream& fin)
{
	fin >> this->vnum;
	fin >> this->arcnum;
	for (int i = 0; i < vnum; i++)
		fin >> this->vertex[i];
	for (int i = 0; i < this->vnum; i++)
		for (int j = 0; j < this->vnum; j++)
			fin >> this->arc[i][j];
}

template<class temp>
m_graph<temp>::m_graph(temp a[], int arc[][maxsize], int vnum, int arcnum)
{
	this->vnum = vnum;
	this->arcnum = arcnum;
	for (int i = 0; i < this->vnum; i++)
		this->vertex[i] = a[i];
	for (int i = 0; i < this->vnum; i++)
		for (int j = 0; j < this->vnum; j++)
			this->arc[i][j] = arc[i][j];
}

student stu[6] =
{
	{1001,"zhang"},{2002,"wang"},{3003,"li"},
	{4004,"zhao"},{5005,"liu"},{6006,"yao"}
};

int arc[maxsize][maxsize] =
{
	{0,1,1,0,0,1},
	{1,0,1,0,1,0},
	{1,1,0,1,0,0},
	{0,0,1,0,0,0},
	{0,1,0,0,0,0},
	{1,0,0,0,0,0},
};
int main()
{
	system("color 0A");
	m_graph<student>mm(stu, arc, 6, 12);
	return 0;
}

2.2测试用图

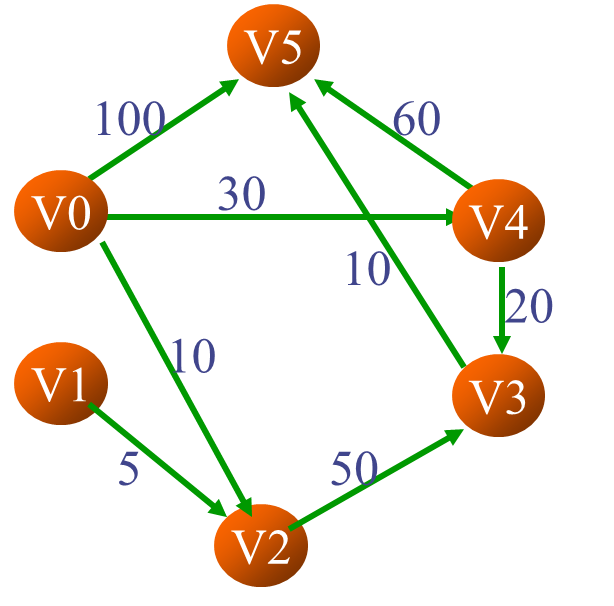
本篇文章讲解的算法采用书上182页图5-34作为例图，用来测试结果。

2.3一个注意事项

使用邻接矩阵作为存储结构时要注意,某结点到自己的距离必须标注为MAX而不是0，不然算法对其修改的时候会出现逻辑错误，导致结果不对。

2.4设置辅助数据结构

​

 三.3个核心函数讲解&&书上代码订正

3.1 short_path函数

这个函数是Dijkstra算法的核心部分，其他两个函数都是为了辅助或者修饰这个函数的。

函数传入两个参数，一个是类操作对象，一个是源点值。源点值是：用户使用Dijkstra算法时要计算到哪个结点的最短距离？这个源点值是用户自定的，因此传参时必不可少。

3.1.1初始化

首先我们应该对辅助数组s进行初始化。s数组每个元素都应更新为false。

*注意*：

有同学会问：既然s数组已经被设置为全局变量了，为什么在这里还要重新初始化一遍呢？

回答：这里s数组的初始化是很必要的。源点的选择是用户自定的，在现实测试中，用户不可能只使用一遍Dijkstra算法，因此不可能只调用一遍short_path函数，因此当调用次数大于等于2次时，如果s数组没有重新初始化，上一次的结果将会影响下一次的运算，所以这里s数组的初始化必不可少。

然后我们应该对disk数组和path数组初始化。根据用户传参的源点不同，disk数组传入 到该源点所有结点的权值，也就是二维数组arc中某一行（列）。path数组初始化的方法就是，除非和源点没有直接相连，否则全部初始化为源结点的下标。

初始化部分的代码：

	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;//v是传参，源点值，也就是源点下标
	disk[v] = 0;

3.1.2迭代更新

按下标遍历所有结点，对某次遍历：

        寻找离源点最近的结点，将下标值赋值给传参v，将v标记为访问过，将v作为转发结点：

                按下标遍历所有结点，如果遍历到某个结点vi，加入了转发结点之后，

                源点到该结点的 路径权值和 比原先的disk[ i ]小，

                那就更新disk[ i ]为这个最小值，同时将path数组该结点的位置的元素标记为v。

解释一下最后一行话的意思：将path[ i ]标记为v代表什么意思？

答：就是，加入了转发结点v之后，到源点到下标为i的结点路径更短了。因为有了v的出现，优化了结果，vi就想记录一下，从家到我这儿，经过v这个地方，比原先路程更短了呢。

迭代更新部分代码为：

	for (int i = 0; i < graph.vnum; i++)
	{
		v = find_min(graph);
		if (v == -1)
		{
			print(graph.vnum);
			return;
		}
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				disk[j] = graph.arc[v][j] + disk[v];
				path[j] = v;
			}
	}

3.1.3一个错误

书上代码这样写：

template<class temp>
void m_graph<temp>::short_path(m_graph<temp>graph, int v)
{
	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;
	disk[v] = 0;
	for (int i = 0; i < graph.vnum; i++)
	{
		v = find_min(graph);
		if (v == -1)
			return;
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				disk[j] = graph.arc[v][j] + disk[v];
				path[j] = v;
			}
	}
	print(graph.vnum);
}

我们可以看到，第二个for循环的循环结束条件是v==-1，执行return ; 语句，但是如果这样，函数直接结束，无法执行最后一行的print函数了。

修改方法1：

template<class temp>
void m_graph<temp>::short_path(m_graph<temp>graph, int v)
{
	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;
	disk[v] = 0;
	for (int i = 0; i < graph.vnum; i++)
	{
		v = find_min(graph);
		if (v == -1)
		{
			print(graph.vnum);//放到这里来
			return;
		}
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				disk[j] = graph.arc[v][j] + disk[v];
				path[j] = v;
			}
	}
}

 修改方法2：将return；改为break；

template<class temp>
void m_graph<temp>::short_path(m_graph<temp>graph, int v)
{
	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;
	disk[v] = 0;
	for (int i = 0; i < graph.vnum; i++)
	{
		v = find_min(graph);
		if (v == -1)
			break;
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				disk[j] = graph.arc[v][j] + disk[v];
				path[j] = v;
			}
	}
	print(graph.vnum);
}

3.1.3short_path函数整体代码

：

template<class temp>
void m_graph<temp>::short_path(m_graph<temp>graph, int v)
{
	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;
	disk[v] = 0;
	for (int i = 0; i < graph.vnum; i++)
	{
		v = find_min(graph);
		if (v == -1)
		{
			print(graph.vnum);
			return;
		}
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				disk[j] = graph.arc[v][j] + disk[v];
				path[j] = v;
			}
	}
}

3.2 find_min函数

此函数的功能是：在disk[ 1…n ]中寻找路径最小值，即离源点最近的结点。 

比较简单，过程不赘述了，代码如下：

template<class temp>
int m_graph<temp>::find_min(m_graph<temp>graph)
{
	int k = 0;
	int min = MAX;
	for (int i = 0; i < graph.vnum; i++)
	{
		if ((!s[i]) && (min > disk[i]))
		{
			min = disk[i];
			k = i;
		}
	}
	if (min == MAX)
		return -1;//表示所有顶点都无法到达源点了
	return k;
}

3.3打印路径

        打印路径主要利用的是path这个辅助数组。path数组的核心思想是，下标和存储数据的妙用。每个下标都存储一个数据，对其中某一组数据+下标（第i组），其代表的真正含义如下：从源点到第i个结点，第一步要走过的结点的下标是path[ i ]。

        这里也是一个迭代思想的体现：如果已知某条路径最短，那么这条路径的子路径也最短。打比喻说：已知始发站到终点站路程最短，那么到途经站的路程也是最短的。

        因此，循环的终止条件是，最终查找到源点自己头上。过程是，从下标0开始，遍历path数组，对某一次遍历：

        取出存储在这个地方的值，将这个值作为下标，找path[ 下标 ]的值，再按照前面的步骤迭代……直到查找到源点自己头上。

打印函数的代码如下：

template<class temp>
void m_graph<temp>::print(int n)
{
	for (int i = 0; i < n; i++)
		if (disk[i] != MAX)
		{
			cout << "V" << i << ":" << disk[i] << "\t{V" << i;
			int pre = path[i];
			while (pre != -1)
            //如果某个存储的元素是-1，
            //则代表这个元素的下标对应的结点是源点
			{
				cout << "V" << pre;

				pre = path[pre];
			}
			cout << "}" << endl;
		}
}

四.通过测试了解核心函数对各种数据的处理

以源点为v0为例，测试书上182页图5-34，对每次数据修改，都将重新输出一遍所有的辅助数据和辅助数组。我们来对比书上的分析图看运行结果：

4.1有向带权图：

4.2数字化为二维数组：

 

4.3 Dijkstra算法分析：

横坐标是操作第i次，纵坐标是终点。

4.4测试结果：

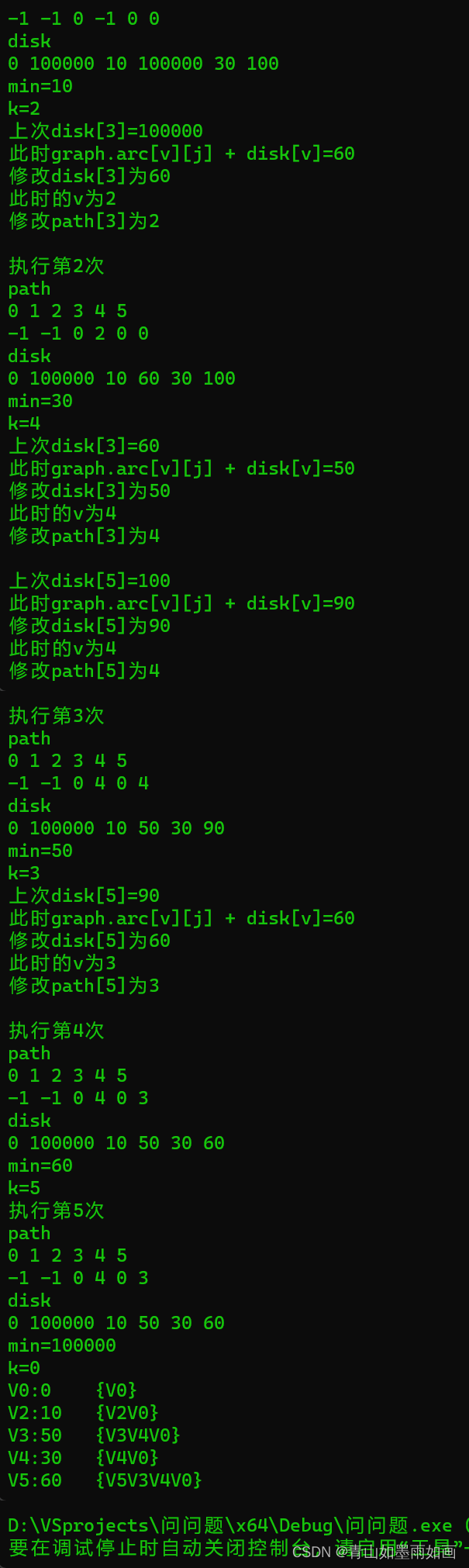
4.5 测试结果对比分析：

每次操作输出中： 

操作第i次

path

下标0~5

每个下标里存储的元素

disk数组

遍历展现

min是：find_min函数每次操作寻找的最小权值

k是：find_min函数返回值，最小权值对应的终点下标，如果k=5然后k=0，说明最短路径找完了。

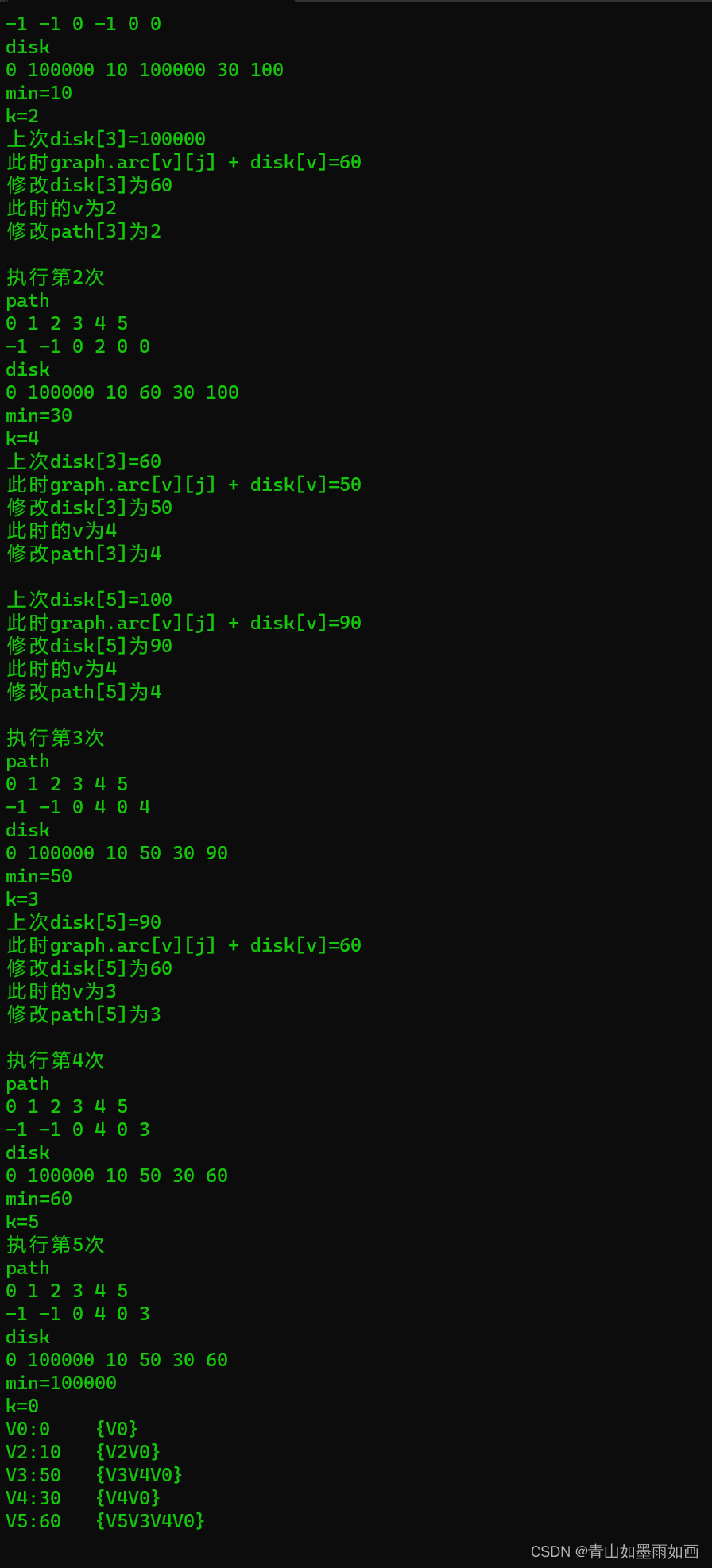
后面为数据优化更新部分。

 执行第一次：

  执行第二次：

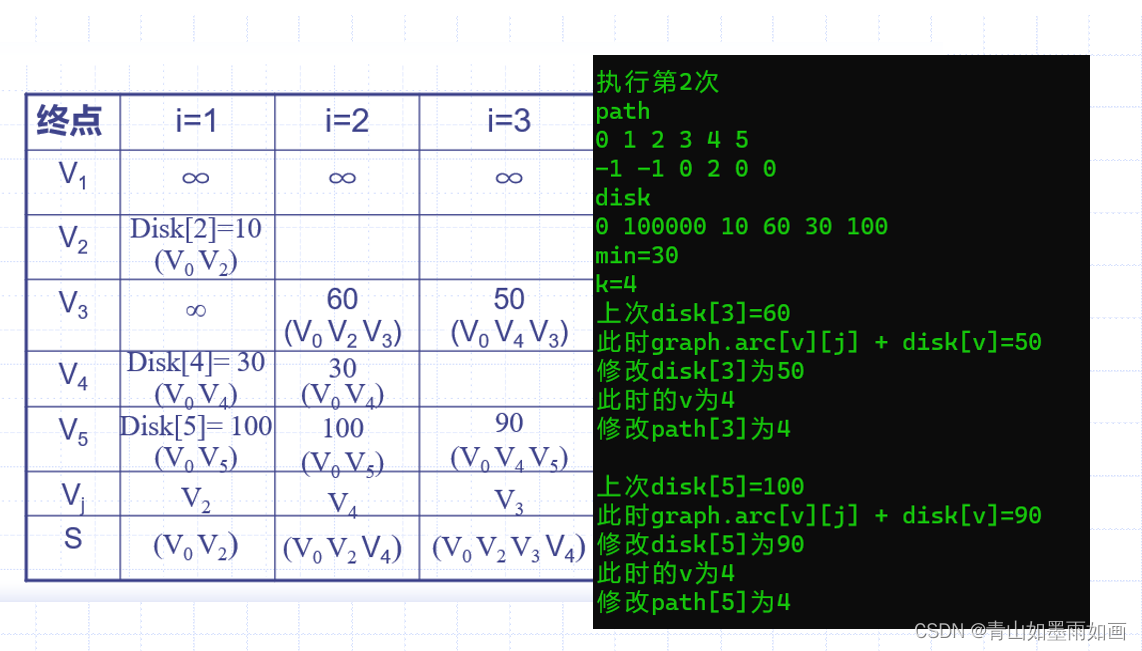
  执行第三次：

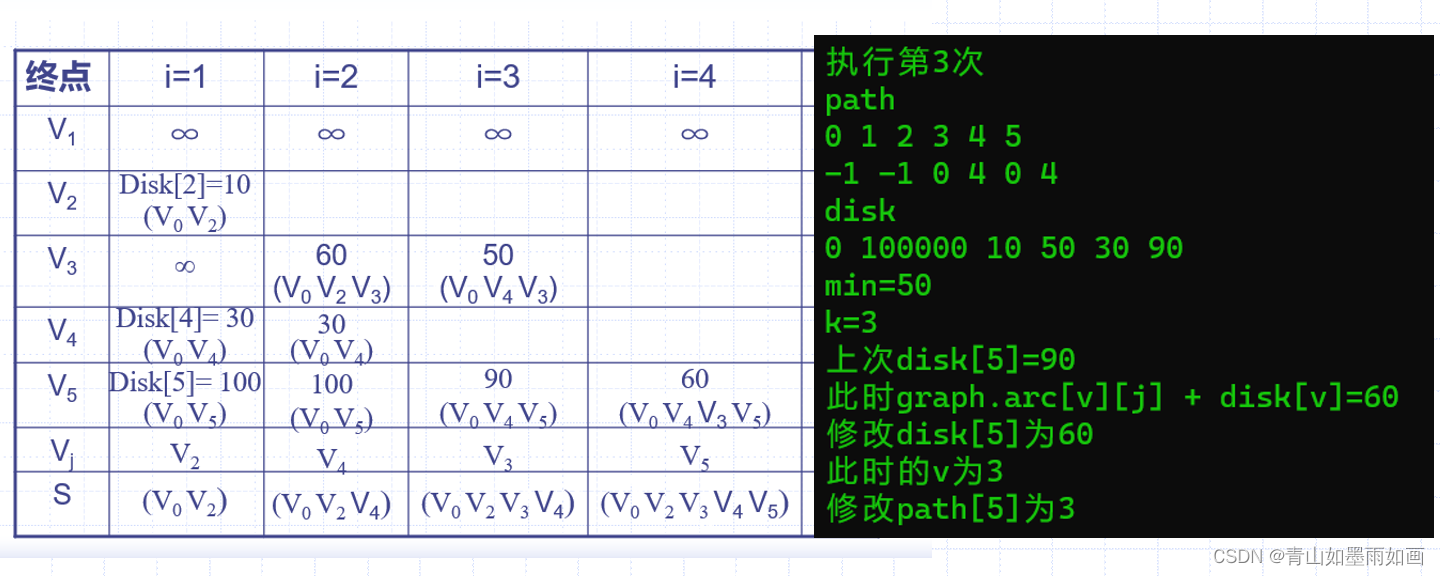
 执行第四次：

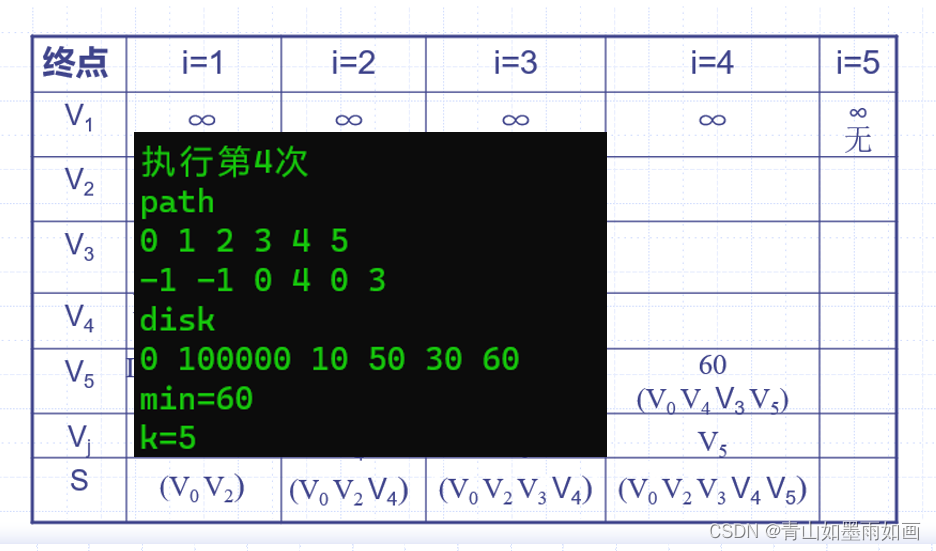
 执行第五次：

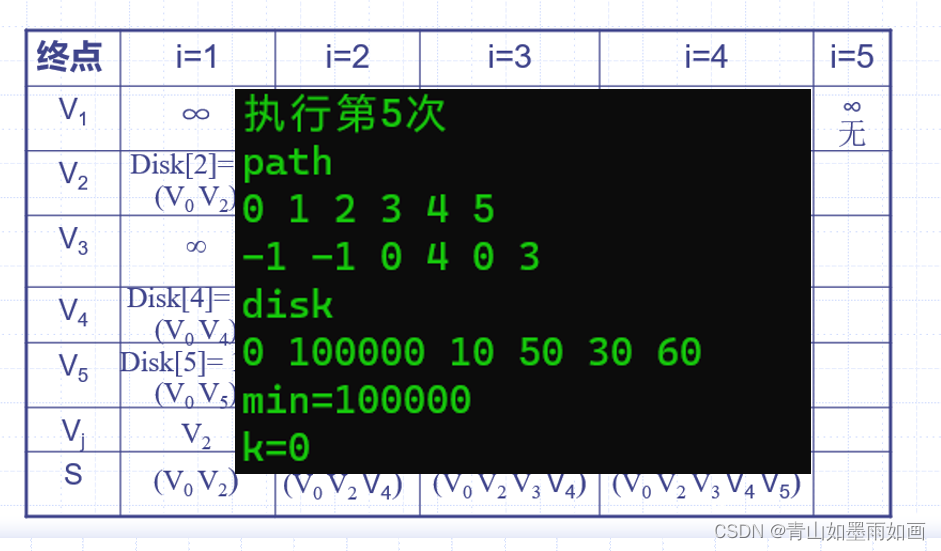
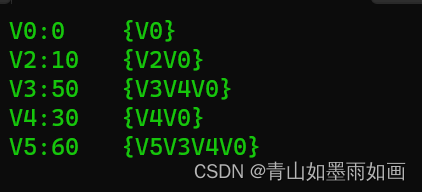
最终结果 

4.6举例分析

通过一系列操作，我们最终确定了path数组中各个元素。现在我们以从v0到v5为例，利用path数组，追溯print算法，看看到底怎么用的。

最终确定的path数组如上图所示，

path[0]=-1,path[1]=-1,path[2]=0,path[3]=4,path[4]=0,path[5]=3。

取i=5；

cout<< V5 : 60 {V

pre=path[5]=3;

cout<<3;

pre=path[path[5]]=path[3]=4;

cout<<V4;

pre=pre[4]=0;

cout<<V0;

pre=pre[0]=-1;

cout<<};

结束。

五.总体代码

5.1含测试代码的总体代码

5.1.1代码效果图

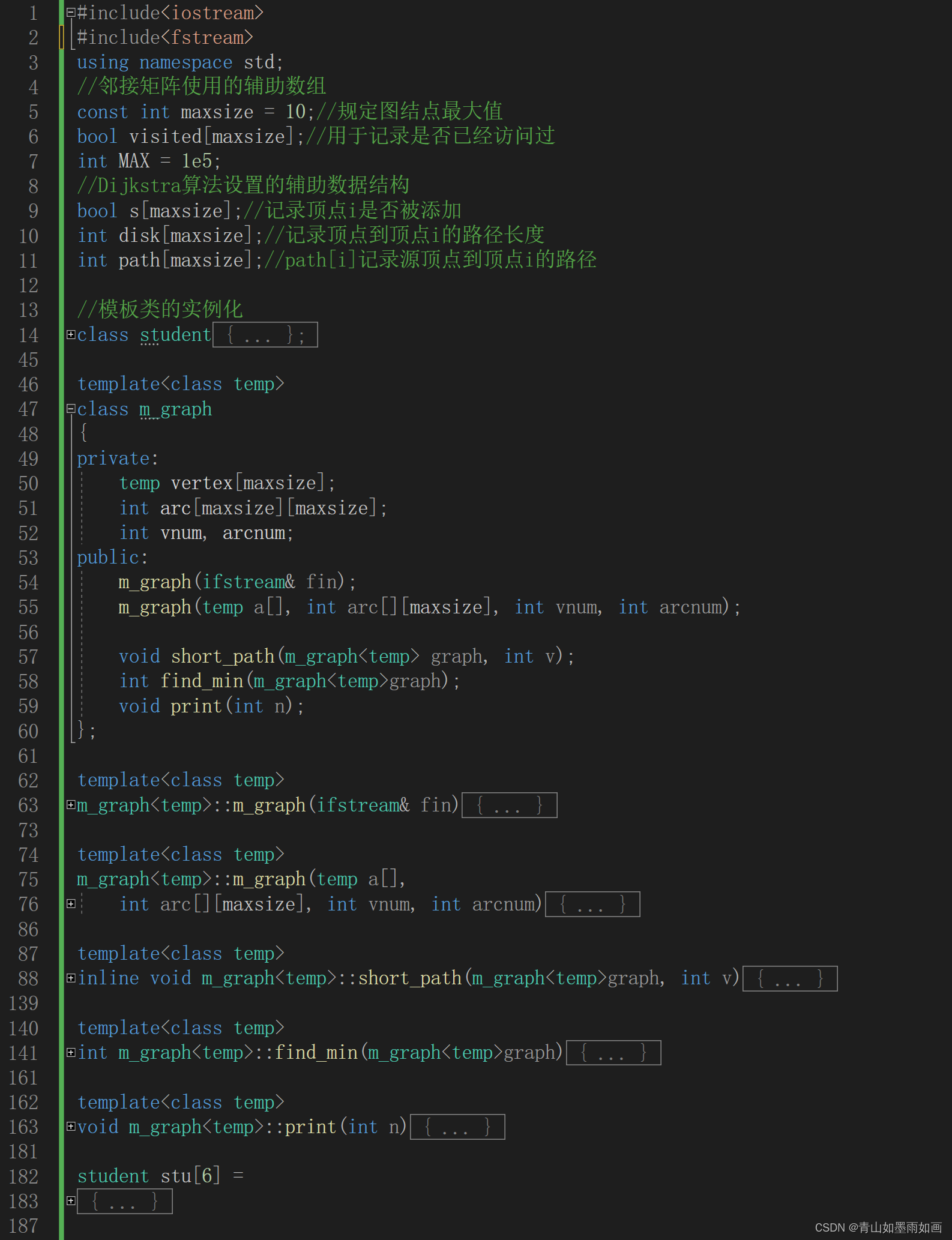
  5.1.2代码部分

#include<iostream>
#include<fstream>
using namespace std;
//邻接矩阵使用的辅助数组
const int maxsize = 10;//规定图结点最大值
bool visited[maxsize];//用于记录是否已经访问过
int MAX = 1e5;
//Dijkstra算法设置的辅助数据结构
bool s[maxsize];//记录顶点i是否被添加
int disk[maxsize];//记录顶点到顶点i的路径长度
int path[maxsize];//path[i]记录源顶点到顶点i的路径

//模板类的实例化
class student
{
private:
	int ID;
	string name;
public:
	student()
	{
		this->ID = 0;
		this->name = "un_known name";
	}
	student(int ID, string name)
	{
		this->ID = ID;
		this->name = name;
	}
	void print()
	{
		cout << "ID:" << this->ID << "  name:" << this->name << endl;
	}
	friend fstream& operator>>(fstream& fin, student& s)
	{
		fin >> s.ID;
		fin >> s.name;
		return fin;
	}
	friend ostream& operator<<(ostream& output, student& s)
	{
		cout << "ID:" << s.ID << "  name:" << s.name;
	}
};

template<class temp>
class m_graph
{
private:
	temp vertex[maxsize];
	int arc[maxsize][maxsize];
	int vnum, arcnum;
public:
	m_graph(ifstream& fin);
	m_graph(temp a[], int arc[][maxsize], int vnum, int arcnum);

	void short_path(m_graph<temp> graph, int v);
	int find_min(m_graph<temp>graph);
	void print(int n);
};

template<class temp>
m_graph<temp>::m_graph(ifstream& fin)
{
	fin >> this->vnum;
	fin >> this->arcnum;
	for (int i = 0; i < vnum; i++)
		fin >> this->vertex[i];
	for (int i = 0; i < this->vnum; i++)
		for (int j = 0; j < this->vnum; j++)
			fin >> this->arc[i][j];
}

template<class temp>
m_graph<temp>::m_graph(temp a[], 
	int arc[][maxsize], int vnum, int arcnum)
{
	this->vnum = vnum;
	this->arcnum = arcnum;
	for (int i = 0; i < this->vnum; i++)
		this->vertex[i] = a[i];
	for (int i = 0; i < this->vnum; i++)
		for (int j = 0; j < this->vnum; j++)
			this->arc[i][j] = arc[i][j];
}

template<class temp>
inline void m_graph<temp>::short_path(m_graph<temp>graph, int v)
{
	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;
	disk[v] = 0;
	for (int i = 0; i < graph.vnum; i++)
	{
		//测试1
		cout << "执行第"<<i+1<<"次" << endl;
		cout << "path" << endl;
		cout << "0 1 2 3 4 5" << endl;
		for (int i = 0; i < graph.vnum; i++)
			cout << path[i] << " ";
		cout << endl;
		cout << "disk" << endl;
		for (int i = 0; i < graph.vnum; i++)
			cout << disk[i] << " ";
		cout << endl;
		//
		v = find_min(graph);
		if (v == -1)
		{
			print(graph.vnum);
			return;
		}
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				//测试2
				cout << "上次disk[" << j << "]=" << disk[j] << endl;
				cout << "此时graph.arc[v][j] + disk[v]=" << graph.arc[v][j] + disk[v] << endl;
				//
				disk[j] = graph.arc[v][j] + disk[v];
				//测试3
				cout << "修改disk[" << j << "]为" << disk[j] << endl;
				cout << "此时的v为" << v << endl;
				cout << "修改path[" << j << "]为" << v << endl << endl;
				//
				path[j] = v;
			}
	}
}

template<class temp>
int m_graph<temp>::find_min(m_graph<temp>graph)
{
	int k = 0;
	int min = MAX;
	for (int i = 0; i < graph.vnum; i++)
	{
		if ((!s[i]) && (min > disk[i]))
		{
			min = disk[i];
			k = i;
		}
	}
	//检测
	cout << "min=" << min << endl;
	cout << "k=" << k << endl;
	//
	if (min == MAX)
		return -1;
	return k;
}

template<class temp>
void m_graph<temp>::print(int n)
{
	for (int i = 0; i < n; i++)
	{
		if(disk[i]!=MAX)
		{
			cout << "V" << i << ":" << disk[i] << "\t{V" << i;
			int pre = path[i];
			while (pre != -1)
			{
				cout << "V" << pre;

				pre = path[pre];
			}
			cout << "}" << endl;
		}
	}
}

student stu[6] =
{
	{1001,"zhang"},{2002,"wang"},{3003,"li"},
	{4004,"zhao"},{5005,"liu"},{6006,"yao"}
};

int arc1[maxsize][maxsize] =
{
	{0,1e5,10,1e5,30,100},//如果到自己不改的话那就一直是0，无法跳出循环
	{1e5,0,5,1e5,1e5,1e5},
	{1e5,1e5,0,50,1e5,1e5},
	{1e5,1e5,1e5,0,1e5,10},
	{1e5,1e5,1e5,20,0,60},
	{1e5,1e5,1e5,1e5,1e5,0}
};
int arc2[maxsize][maxsize] =
{
	{1e5,1e5,10,1e5,30,100},
	{1e5,1e5,5,1e5,1e5,1e5},
	{1e5,1e5,1e5,50,1e5,1e5},
	{1e5,1e5,1e5,1e5,1e5,10},
	{1e5,1e5,1e5,20,1e5,60},
	{1e5,1e5,1e5,1e5,1e5,1e5}
};

int main()
{
	system("color 0A");
	m_graph<student>m5(stu, arc2, 6, 12);
	m5.short_path(m5, 0);
	return 0;
}

5.1.3代码运行结果

 5.2不含测试代码的总体代码（书上代码）

5.2.1代码效果图

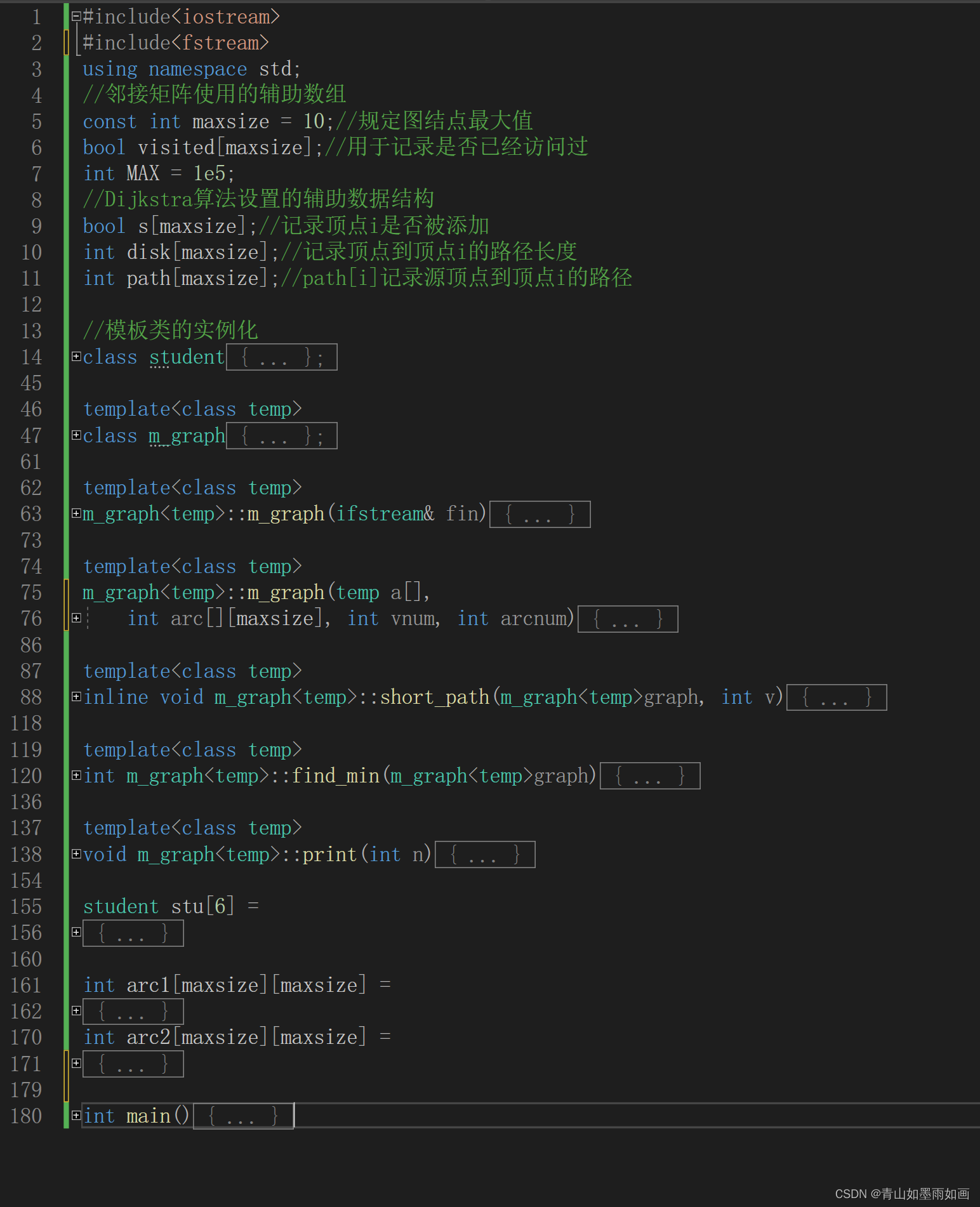
5.2.2代码部分

#include<iostream>
#include<fstream>
using namespace std;
//邻接矩阵使用的辅助数组
const int maxsize = 10;//规定图结点最大值
bool visited[maxsize];//用于记录是否已经访问过
int MAX = 1e5;
//Dijkstra算法设置的辅助数据结构
bool s[maxsize];//记录顶点i是否被添加
int disk[maxsize];//记录顶点到顶点i的路径长度
int path[maxsize];//path[i]记录源顶点到顶点i的路径

//模板类的实例化
class student
{
private:
	int ID;
	string name;
public:
	student()
	{
		this->ID = 0;
		this->name = "un_known name";
	}
	student(int ID, string name)
	{
		this->ID = ID;
		this->name = name;
	}
	void print()
	{
		cout << "ID:" << this->ID << "  name:" << this->name << endl;
	}
	friend fstream& operator>>(fstream& fin, student& s)
	{
		fin >> s.ID;
		fin >> s.name;
		return fin;
	}
	friend ostream& operator<<(ostream& output, student& s)
	{
		cout << "ID:" << s.ID << "  name:" << s.name;
	}
};

template<class temp>
class m_graph
{
private:
	temp vertex[maxsize];
	int arc[maxsize][maxsize];
	int vnum, arcnum;
public:
	m_graph(ifstream& fin);
	m_graph(temp a[], int arc[][maxsize], int vnum, int arcnum);

	void short_path(m_graph<temp> graph, int v);
	int find_min(m_graph<temp>graph);
	void print(int n);
};

template<class temp>
m_graph<temp>::m_graph(ifstream& fin)
{
	fin >> this->vnum;
	fin >> this->arcnum;
	for (int i = 0; i < vnum; i++)
		fin >> this->vertex[i];
	for (int i = 0; i < this->vnum; i++)
		for (int j = 0; j < this->vnum; j++)
			fin >> this->arc[i][j];
}

template<class temp>
m_graph<temp>::m_graph(temp a[], 
	int arc[][maxsize], int vnum, int arcnum)
{
	this->vnum = vnum;
	this->arcnum = arcnum;
	for (int i = 0; i < this->vnum; i++)
		this->vertex[i] = a[i];
	for (int i = 0; i < this->vnum; i++)
		for (int j = 0; j < this->vnum; j++)
			this->arc[i][j] = arc[i][j];
}

template<class temp>
inline void m_graph<temp>::short_path(m_graph<temp>graph, int v)
{
	for (int i = 0; i < graph.vnum; i++)
	{
		s[i] = false;//必要性
		disk[i] = graph.arc[v][i];
		if (disk[i] != MAX)
			path[i] = v;
		else
			path[i] = -1;
	}
	s[v] = 1;
	disk[v] = 0;
	for (int i = 0; i < graph.vnum; i++)
	{
		v = find_min(graph);
		if (v == -1)
		{
			print(graph.vnum);
			return;
		}
		s[v] = true;
		for (int j = 0; j < graph.vnum; j++)
			if ((!s[j]) && (disk[j] > graph.arc[v][j] + disk[v]))
			{
				disk[j] = graph.arc[v][j] + disk[v];
				path[j] = v;
			}
	}
}

template<class temp>
int m_graph<temp>::find_min(m_graph<temp>graph)
{
	int k = 0;
	int min = MAX;
	for (int i = 0; i < graph.vnum; i++)
	{
		if ((!s[i]) && (min > disk[i]))
		{
			min = disk[i];
			k = i;
		}
	}
	if (min == MAX)
		return -1;
	return k;
}

template<class temp>
void m_graph<temp>::print(int n)
{
	for (int i = 0; i < n; i++)
		if (disk[i] != MAX)
		{
			cout << "V" << i << ":" << disk[i] << "\t{V" << i;
			int pre = path[i];
			while (pre != -1)
			{
				cout << "V" << pre;

				pre = path[pre];
			}
			cout << "}" << endl;
		}
}

student stu[6] =
{
	{1001,"zhang"},{2002,"wang"},{3003,"li"},
	{4004,"zhao"},{5005,"liu"},{6006,"yao"}
};

int arc1[maxsize][maxsize] =
{
	{0,1e5,10,1e5,30,100},//如果到自己不改的话那就一直是0，无法跳出循环
	{1e5,0,5,1e5,1e5,1e5},
	{1e5,1e5,0,50,1e5,1e5},
	{1e5,1e5,1e5,0,1e5,10},
	{1e5,1e5,1e5,20,0,60},
	{1e5,1e5,1e5,1e5,1e5,0}
};
int arc2[maxsize][maxsize] =
{
	{1e5,1e5,10,1e5,30,100},
	{1e5,1e5,5,1e5,1e5,1e5},
	{1e5,1e5,1e5,50,1e5,1e5},
	{1e5,1e5,1e5,1e5,1e5,10},
	{1e5,1e5,1e5,20,1e5,60},
	{1e5,1e5,1e5,1e5,1e5,1e5}
};

int main()
{
	system("color 0A");
	m_graph<student>m5(stu, arc2, 6, 12);
	m5.short_path(m5, 0);
	return 0;
}

5.2.3代码运行结果

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/838981.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

mysql大表的深度分页慢sql案例(跳页分页)

mysql大表的深度分页慢sql案例(跳页分页)

1 背景 有一张表&#xff0c;内容是 redis缓存中的key信息&#xff0c;数据量约1000万级&#xff0c; expiry列上有一个普通B树索引。 -- test.top definitionCREATE TABLE top (database int(11) DEFAULT NULL,type varchar(50) DEFAULT NULL,key varchar(500) DEFAULT NUL…
阅读更多...
java+ssm校园高校足球联赛管理系统tdl2g

java+ssm校园高校足球联赛管理系统tdl2g

随着计算机技术发展&#xff0c;计算机系统的应用已延伸到社会的各个领域&#xff0c;大量基于网络的广泛应用给生活带来了十分的便利。所以把足球联赛管理与现在网络相结合&#xff0c;利用计算机搭建足球联赛管理系统&#xff0c;实现足球联赛管理系统的信息化。则对于进一步…
阅读更多...
直线导轨在视觉检测设备中的应用

直线导轨在视觉检测设备中的应用

随着科技的不断发展&#xff0c;视觉检测设备已经逐渐代替了传统的人工品检&#xff0c;成为了工业生产中的一部分&#xff0c;在五金配件、塑胶件、橡胶件、电子配件等检测工业零部件表面外观缺陷尺寸方面应用&#xff0c;视觉检测设备具有优势。 直线导轨作为视觉检测设备中重…
阅读更多...
EVE-NG MPLS L2VPN static lsp

EVE-NG MPLS L2VPN static lsp

目录 1 拓扑 2 配置步骤 2.1 配置接口IP 和路由协议 2.2 配置MPLS LDP 2.3 配置L2VPN PW 2.4 验证L2VPN 1 拓扑 2 配置步骤 2.1 配置接口IP 和路由协议 PE1 interface LoopBack 0ip address 1.1.1.9 32 quitinterface GigabitEthernet1/0ip address 10.1.1.1 255.255…
阅读更多...
【数理知识】求刚体旋转矩阵和平移矩阵，已知 N＞=3 个点在前后时刻的坐标，且这 N＞=3 点间距离始终不变代表一个刚体

【数理知识】求刚体旋转矩阵和平移矩阵，已知 N＞=3 个点在前后时刻的坐标，且这 N＞=3 点间距离始终不变代表一个刚体

序号内容1【数理知识】自由度 degree of freedom 及自由度的计算方法2【数理知识】刚体 rigid body 及刚体的运动3【数理知识】刚体基本运动&#xff0c;平动&#xff0c;转动4【数理知识】向量数乘&#xff0c;内积&#xff0c;外积&#xff0c;matlab代码实现5【数理知识】协…
阅读更多...
【深度学习_TensorFlow】感知机、全连接层、神经网络

【深度学习_TensorFlow】感知机、全连接层、神经网络

写在前面 感知机、全连接层、神经网络是什么意思&#xff1f; 感知机&#xff1a; 是最简单的神经网络结构&#xff0c;可以对线性可分的数据进行分类。 全连接层&#xff1a; 是神经网络中的一种层结构&#xff0c;每个神经元与上一层的所有神经元相连接,实现全连接。 神经…
阅读更多...
kibana-7.17.3版本安装及汉化

kibana-7.17.3版本安装及汉化

1、官网下载地址&#xff1a;https://www.elastic.co/cn/downloads/kibana 选择安装系统类型和历史版本kibana安装版本要和es版本对应 2、上传安装包然后解压 tar -zxf kibana-7.17.3-linux-x86_64.tar.gz 3、更改目录属主 chown elk. kibana-7.17.3-linux-x86_64 -R …
阅读更多...
C语言笔试训练【第三天】

C语言笔试训练【第三天】

大家好&#xff0c;我是纪宁。 今天是C语言笔试训练的第三天&#xff0c;大家加油&#xff01; 第一题 1、已知函数的原型是&#xff1a; int fun(char b[10], int *a) &#xff0c;设定义&#xff1a; char c[10];int d; &#xff0c;正确的调用语句是&#xff08; &#xf…
阅读更多...
基于Mediapipe的姿势识别并同步到Unity人体模型中

基于Mediapipe的姿势识别并同步到Unity人体模型中

如题&#xff0c;由于是商业项目&#xff0c;无法公开源码&#xff0c;这里主要说一下实现此功能的思路。 人体关节点识别 基于Mediapipe Unity插件进行开发&#xff0c;性能比较低的CPU主机&#xff0c;无法流畅地运行Mediapipe&#xff0c;这个要注意一下。 Mediapipe33个人体…
阅读更多...
STM32F103——基础篇

STM32F103——基础篇

目录 1、寄存器基础知识 2、STM32F103系统架构 2.1 Cortex M3 内核&芯片 2.2 STM32F103系统架构 3、存储器映射 4、寄存器映射 4.1 寄存器描述解读 4.2 寄存器映射举例 4.3 寄存器地址计算 4.4 stm32f103xe.h 寄存器映射 1、寄存器基础知识 概念&#xff1a;寄存…
阅读更多...
【C语言进阶】指针的高级应用（上）

【C语言进阶】指针的高级应用（上）

本专栏介绍&#xff1a;免费专栏&#xff0c;并且会持续更新C语言基础知识&#xff0c;欢迎各位订阅关注。 关注我&#xff0c;带你了解更多关于机器人、嵌入式、人工智能等方面的优质文章&#xff0c;坚持更新&#xff01; 大家的支持才是更新的最强动力&#xff01; 文章目录…
阅读更多...
详解PHP反射API

详解PHP反射API

PHP中的反射API就像Java中的java.lang.reflect包一样。它由一系列可以分析属性、方法和类的内置类组成。它在某些方面和对象函数相似&#xff0c;比如get_class_vars()&#xff0c;但是更加灵活&#xff0c;而且可以提供更多信息。反射API也可与PHP最新的面向对象特性一起工作&…
阅读更多...
掌握 JVM 的参数及配置

掌握 JVM 的参数及配置

点击下方关注我&#xff0c;然后右上角点击...“设为星标”&#xff0c;就能第一时间收到更新推送啦~~~ JVM&#xff08;Java虚拟机&#xff09;是Java编程语言的核心组件之一&#xff0c;它负责执行Java程序&#xff0c;并提供一系列参数和配置选项&#xff0c;可以调整Java程…
阅读更多...
探秘企业DevOps一体化平台建设终极形态丨IDCF

探秘企业DevOps一体化平台建设终极形态丨IDCF

笔者从事为企业提供研发效能改进解决方案相关工作十几年&#xff0c;为国内上百家企业提供过DevOps咨询及解决方案落地解决方案&#xff0c;涉及行业包括&#xff1a;金融、通信、制造、互联网、快销等多种行业。 DevOps的核心是研发效能改进&#xff0c;效能的提升离不开强大…
阅读更多...
Linux基本开发工具(一)

Linux基本开发工具(一)

文章目录 Linux基本开发工具&#xff08;一&#xff09;Linux安装和卸载软件Linux 软件包管理器 yum关于sudo命令关于yum源的换源问题 vim编辑器的使用vim三种模式&#xff08;常见&#xff09;vim的基本操作vim配置 Linux基本开发工具&#xff08;一&#xff09; Linux安装和…
阅读更多...
Dubbo中使用netty

Dubbo中使用netty

技术主题 netty在Dubbo中的使用，主要集中在网络通信上， 技术原理 Dubbo是什么 高性能、轻量级的开源java的RPC框架，提供三大核心能力：面向接口的远程方法调用，智能容错和负载均衡，以及服务自动注册和发现。 Dubbo的传输结构 1、魔数标识符（四个字节），用于区分不同…
阅读更多...
机器人开发--兴颂雷达介绍

机器人开发--兴颂雷达介绍

机器人开发--兴颂雷达介绍 1 介绍2 使用手册参考 1 介绍 佛山市兴颂机器人科技有限公司&#xff08;Hinson&#xff09;是一家集研发、设计、生产、销售机器人(AGV)导航核心零部件、并提供整体运动控制方案的自主创新型国家高新技术企业。 2 使用手册 兴颂激光雷达使…
阅读更多...
HDFS中的sequence file

HDFS中的sequence file

sequence file序列化文件 介绍优缺点格式未压缩格式基于record压缩格式基于block压缩格式 介绍 sequence file是hadoop提供的一种二进制文件存储格式一条数据称之为record&#xff08;记录&#xff09;&#xff0c;底层直接以<key, value>键值对形式序列化到文件中 优…
阅读更多...
【flink】开启savepoint

【flink】开启savepoint

先启动一个任务 flink run -c com.yang.flink.CDCJob test-cdc.jar开启savepoint 命令&#xff1a; flink savepoint JobID 文件地址 flink savepoint e929a11d79bdc5e6f140f2cfb92e1335 file:///workspace/flinkSavepoints/backend这样就开启好了 操作中的错误 详细信…
阅读更多...
HTTP——八、确认访问用户身份的认证

HTTP——八、确认访问用户身份的认证

HTTP 一、何为认证二、BASIC认证BASIC认证的认证步骤 三、DIGEST认证DIGEST认证的认证步骤 四、SSL客户端认证1、SSL 客户端认证的认证步骤2、SSL 客户端认证采用双因素认证3、SSL 客户端认证必要的费用 五、基于表单认证1、认证多半为基于表单认证2、Session 管理及 Cookie 应…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023