目录

216. 组合总和 III

17. 电话号码的字母组合

---

216. 组合总和 III

难度：medium

类型：回溯

思路：

        与77组合类似的题目。 

        代码随想录算法训练营day24 | 回溯问题，77. 组合_Chamberlain T的博客-CSDN博客

        注意两处剪枝。 

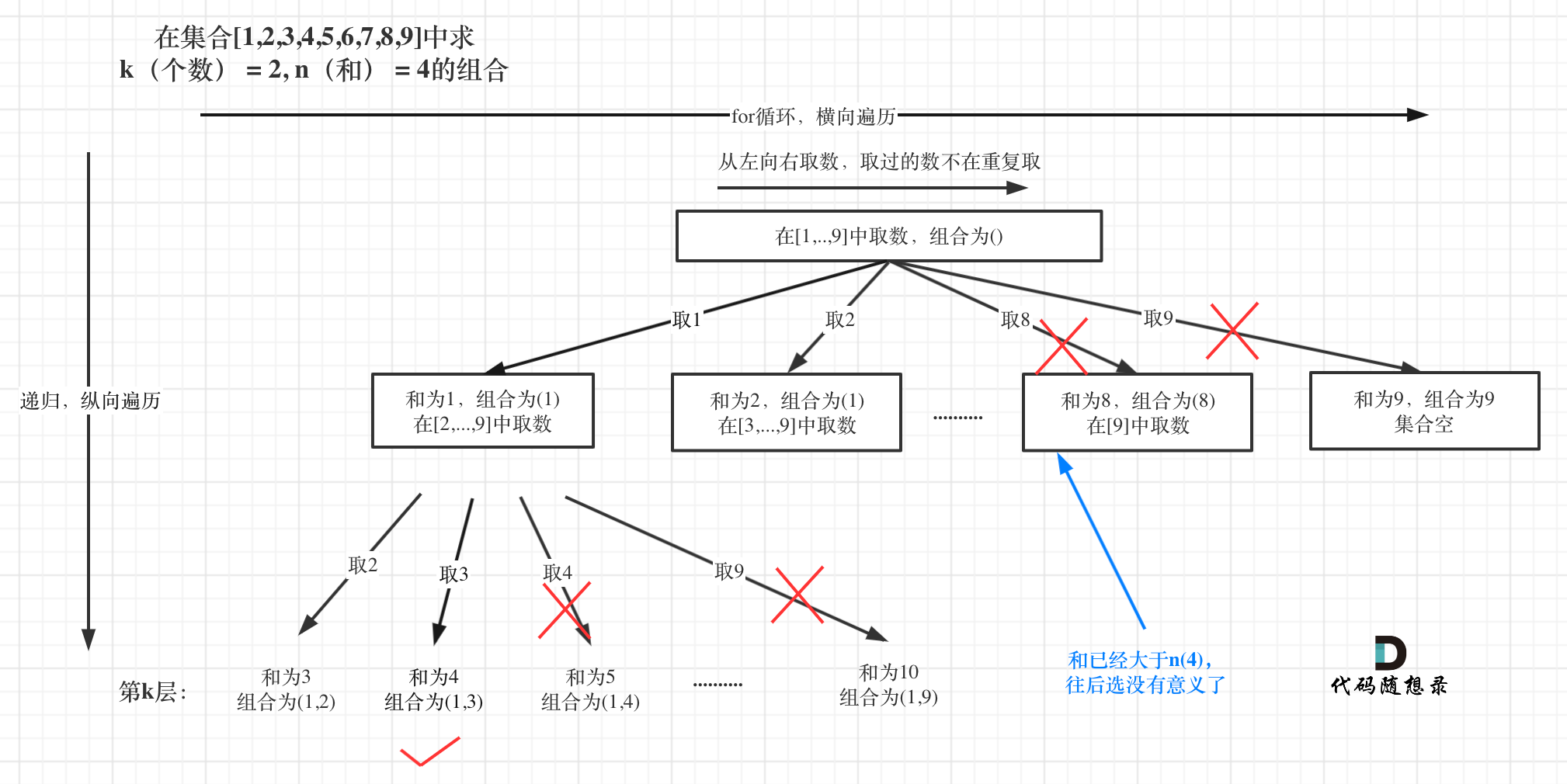
代码：

class Solution {
    private int sum = 0;
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> ans = new ArrayList<>();
  
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(n, k, 1);
        return ans;
    }
 
    public void backtracking(int n, int k, int startIndex) {
        // 剪枝
        if (sum > n) {
            return;
        }

        if (path.size() == k) {
            if (sum == n) {
                // 创建一个新的List，避免传递path的引用
                ans.add(new ArrayList<>(path));
            }
            return;
        }
        // 剪枝：i <= 9 - (k - path.size()) + 1
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
            sum += i;
            path.add(i);
            backtracking(n, k, i + 1);
            sum -= i;
            path.remove(path.size() - 1);
        }
    }
}

• 时间复杂度: O(n * 2^n)
• 空间复杂度: O(n)

17. 电话号码的字母组合

难度：medium

类型：回溯

思路：

        

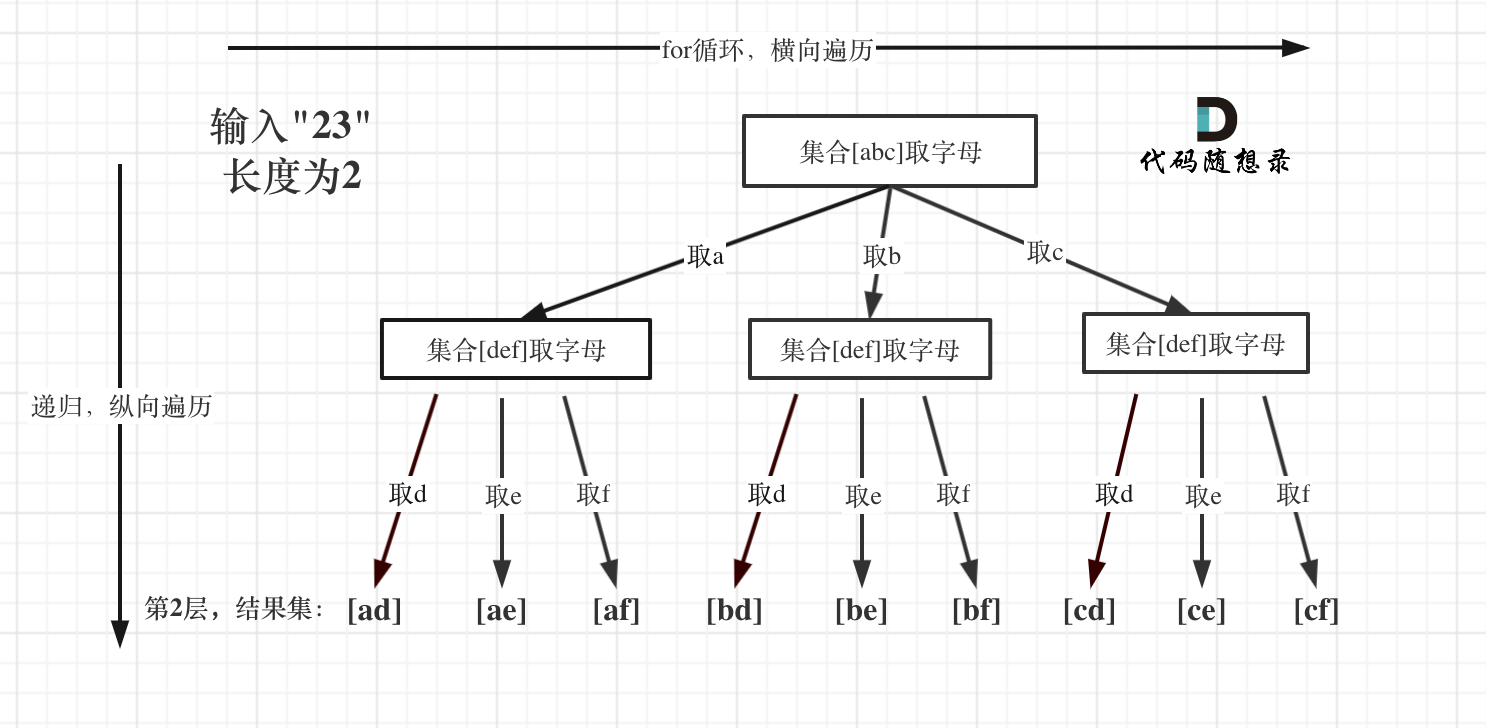
         递归二叉树的深度为电话号码的长度，每层递归的宽度为对应的号码的字符串长度；

        纵向递归号码每个数字，横向遍历每个数字下的字符串的每个字母。

代码：

class Solution {
    private List<String> ans = new ArrayList<>();
    private String[] phoneNums = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    private StringBuffer sb = new StringBuffer(); 
    // 数字纵向递归，字母横向遍历
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return ans;
        }
        backtracking(digits, 0);
        return ans;
    }

    public void backtracking(String digits, int startIndex) {
        if (sb.length() == digits.length()) {
            ans.add(sb.toString());
            return;
        }
        // 本层递归遍历的字符串及其对应的数组下标
        int num = digits.charAt(startIndex) - '0';
        String str = phoneNums[num];
        for (int i = 0; i < str.length(); i++) {
            sb.append(str.charAt(i));
            backtracking(digits, startIndex + 1);
            sb.deleteCharAt(sb.length() - 1);
        }
    }
}

• 时间复杂度: O(3^m * 4^n)，其中 m 是对应四个字母的数字个数，n 是对应三个字母的数字个数 (为什么？)
• 空间复杂度: O(3^m * 4^n)