1.简述
多目标规划的一种求解方法是加权系数法,即为每一个目标赋值一个权系数,把多目标模型转化为一个单目标模型。MATLAB的fgoalattain()函数可以用于求解多目标规划。
基本语法
fgoalattain()函数的用法:
x = fgoalattain(fun,x0,goal,weight)
x = fgoalattain(fun,x0,goal,weight,A,b)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq)
x=fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub)
x=fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon)
x=fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fgoalattain(problem)
[x,fval] = fgoalattain(......)
[x,fval,attainfactor,exitflag,output] = fgoalattain(......)
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(......)
其中fun 是用 M 文件定义的目标向量函数,x0 是初值,weight 是权重。
A,b 定义不等式约束A*x ≤ b ,Aeq,beq定义等式约束 Aeq*x=Beq ,
nonlcon是用 M 文件定义的非线性约束c(x) ≤0,ceq(x)=0 。返回值 fval是目标向量函数的值。
要完整掌握其用法,请用 help fgoalattain 或 type fgoalattain 查询相关的帮助。多目标规划问题的描述
多目标问题可以描述成如下问题:
(x)为待优化的目标函数;x为待优化的变量;lb和ub分别为变量x的下限和上限约束;Aeq∗
也就是说,某一个目标函数的提高需要以另一个目标函数的降低作为代价,我们称这样的解A和B是非劣解,或者说是帕累托最优解,多目标规划问题就是要求解这些帕累托最优解。
2. 求解多目标优化问题方法
目前求解多目标优化问题方法算法主要有基于数学的规划方法和基于遗传算法的两类方法;其中带精英策略的快速非支配排序算法(NSGA-II)是影响最大和应用范围最广的一种多目标遗传算法。在其出现以后,由于它简单有效以及比较明显的优越性,使得该算法已经成为多目标优化问题中的基本算法之一,该算法主要优点:
提出了快速非支配的排序算法,降低了计算非支配序的复杂度。
引入了精英策略,扩大了采样空间。将父代种群与其产生的子代种群组合在一起,共同通过竞争来产生下一代种群,这有利于是父代中的优良个体得以保持,保证那些优良的个体在进化过程中不被丢弃,从而提高优化结果的准确度。并且通过对种群所有个体分层存放,使得最佳个体不会丢失,能够迅速提高种群水平。
引入拥挤度和拥挤度比较算子,这不但克服了NSGA算法中需要人为指定共享参数的缺陷,而且将拥挤度作为种群中个体之间的比较准则,使得准Pareto域中的种群个体能均匀扩展到整个Pareto域,从而保证了种群的多样性。
3.matlab求解
Matlab中提供函数gamultiobj采用的算法就是基于NSGA-II改进的一种多目标优化算法(a variant of NSGA-II),接下来对目标规划中的一些概念进行介绍。
3.1 支配(dominate)与非劣(non-inferior)
在多目标规划问题中,如果个体p至少有一个目标比个体q的好,而且个体p的所有目标都不比个体q的差,那么称个体p支配个体q(p dominate q),或者称个体q受个体p支配(q is dominated by p),也可以说,个体p非劣个体q(p is non- inferior to q)。
3.2 序值(rank)和前端(front)
如果p支配q,那么p的序值比q低,如果p和q互不支配,或者说,p和q互相非劣,那么p和q有相同的序值,序值为1的个体属于第一前端,序值为2的个体属于第二前端,依此推类。显然,在当前种群中,第一前端是完全不受支配的,第二前端受第一前端中个体是支配,这样,通过排序,可以将种群中的个体分配到不同的前端。
3.3 拥挤距离(crowding-distance)
拥挤距离用来计算某前端中的某个体与与该前端中其他个体之间的距离,用以表征个体间的拥挤程度。显然,拥挤距离的值越大,个体间就越不用拥挤,种群的多样性就越好。需要指出的是,只有处于同一前端的个体间才需要计算拥挤距离,不同前端之间计算距离是没有意义的。
3.4 最优前端个体系数(paretofraction)
最优前端个体系数定义为最优前端中的个体在种群中所占有的比例,即最优前端个体数=min{paretofraction∗ *∗种群大小,前端中现存的个体数目},其取值范围为[0到1]。
2.代码
主函数:
clc
clear
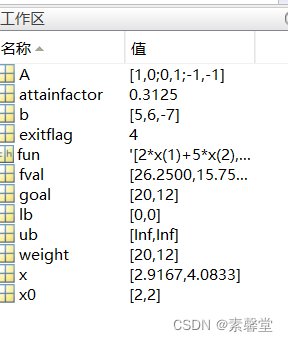
fun='[2*x(1)+5*x(2),4*x(1)+x(2)]';
goal=[20,12];
weight=[20,12];
x0=[2,2];
A=[1 0; 0 1;-1 -1];
b=[5 6 -7];
lb=[0 0];ub=[inf inf];
[x,fval,attainfactor,exitflag]=fgoalattain(fun,x0,goal,weight,A,b,[],[],lb,ub)
子函数:
function [x,FVAL,ATTAINFACTOR,EXITFLAG,OUTPUT,LAMBDA] = fgoalattain(FUN,x,GOAL,WEIGHT,A,B,Aeq,Beq,LB,UB,NONLCON,options,varargin)
%FGOALATTAIN solves the multi-objective goal attainment optimization
% problem.
%
% X = FGOALATTAIN(FUN,X0,GOAL,WEIGHT)
% tries to make the objective functions (F) supplied by the function FUN
% attain the goals (GOAL) by varying X. The goals are weighted according
% to WEIGHT. In doing so the following nonlinear programming problem is
% solved:
% min { GAMMA : F(X)-WEIGHT.*GAMMA<=GOAL }
% X,GAMMA
%
% FUN accepts input X and returns a vector (matrix) of function values F
% evaluated at X. X0 may be a scalar, vector, or matrix.
%
% X = FGOALATTAIN(FUN,X0,GOAL,WEIGHT,A,B) solves the goal attainment
% problem subject to the linear inequalities A*X <= B.
%
% X = FGOALATTAIN(FUN,X0,GOAL,WEIGHT,A,B,Aeq,Beq) solves the goal
% attainment problem subject to the linear equalities Aeq*X = Beq as
% well.
%
% X = FGOALATTAIN(FUN,X0,GOAL,WEIGHT,A,B,Aeq,Beq,LB,UB) defines a set of
% lower and upper bounds on the design variables, X, so that the solution
% is in the range LB <= X <= UB. Use empty matrices for LB and U if no
% bounds exist. Set LB(i) = -Inf if X(i) is unbounded below; set
% UB(i) = Inf if X(i) is unbounded above.
%
% X = FGOALATTAIN(FUN,X0,GOAL,WEIGHT,A,B,Aeq,Beq,LB,UB,NONLCON) subjects
% the goal attainment problem to the constraints defined in NONLCON
% (usually a MATLAB file: NONLCON.m). The function NONLCON should return
% the vectors C and Ceq, representing the nonlinear inequalities and
% equalities respectively, when called with feval:
% [C, Ceq] = feval(NONLCON,X). FGOALATTAIN optimizes such that C(X) <= 0
% and Ceq(X) = 0.
%
% X = FGOALATTAIN(FUN,X0,GOAL,WEIGHT,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS)
% minimizes the with default optimization parameters replaced by values
% in OPTIONS, an argument created with the OPTIMOPTIONS function. See
% OPTIMOPTIONS for details. Use the SpecifyObjectiveGradient option to
% specify that FUN may be called with two output arguments where the
% second, G, is the partial derivatives of the function df/dX, at the
% point X: [F,G] = feval(FUN,X). Use the SpecifyConstraintGradient option
% to specify that NONLCON may be called with four output arguments:
% [C,Ceq,GC,GCeq] = feval(NONLCON,X) where GC is the partial derivatives
% of the constraint vector of inequalities C an GCeq is the partial
% derivatives of the constraint vector of equalities Ceq. Use OPTIONS =
% [] as a place holder if no options are set.
%
% X = FGOALATTAIN(PROBLEM) solves the goal attainment problem defined in
% PROBLEM. PROBLEM is a structure with the function FUN in
% PROBLEM.objective, the start point in PROBLEM.x0, the 'goal' vector in
% PROBLEM.goal, the 'weight' vector in PROBLEM.weight, the linear
% inequality constraints in PROBLEM.Aineq and PROBLEM.bineq, the linear
% equality constraints in PROBLEM.Aeq and PROBLEM.beq, the lower bounds
% in PROBLEM.lb, the upper bounds in PROBLEM.ub, the nonlinear constraint
% function in PROBLEM.nonlcon, the options structure in PROBLEM.options,
% and solver name 'fgoalattain' in PROBLEM.solver. Use this syntax to
% solve at the command line a problem exported from OPTIMTOOL.
%
% [X,FVAL] = FGOALATTAIN(FUN,X0,...) returns the value of the objective
% function FUN at the solution X.
%
% [X,FVAL,ATTAINFACTOR] = FGOALATTAIN(FUN,X0,...) returns the attainment
% factor at the solution X. If ATTAINFACTOR is negative, the goals have
% been over- achieved; if ATTAINFACTOR is positive, the goals have been
% under-achieved.
%
% [X,FVAL,ATTAINFACTOR,EXITFLAG] = FGOALATTAIN(FUN,X0,...) returns an
% EXITFLAG that describes the exit condition. Possible values of EXITFLAG
% and the corresponding exit conditions are listed below. See the
% documentation for a complete description.
%
% 1 FGOALATTAIN converged to a solution.
% 4 Computed search direction too small.
% 5 Predicted change in ATTAINFACTOR too small.
% 0 Too many function evaluations or iterations.
% -1 Stopped by output/plot function.
% -2 No feasible point found.
%
% [X,FVAL,ATTAINFACTOR,EXITFLAG,OUTPUT] = FGOALATTAIN(FUN,X0,...) returns
% a structure OUTPUT with the number of iterations taken in
% OUTPUT.iterations, the number of function evaluations in
% OUTPUT.funcCount, the norm of the final step in OUTPUT.stepsize, the
% final line search steplength in OUTPUT.lssteplength, the algorithm used
% in OUTPUT.algorithm, the first-order optimality in
% OUTPUT.firstorderopt, and the exit message in OUTPUT.message.
%
% [X,FVAL,ATTAINFACTOR,EXITFLAG,OUTPUT,LAMBDA] = FGOALATTAIN(FUN,X0,...)
% returns the Lagrange multiplier at the solution X: LAMBDA.lower for
% LB, LAMBDA.upper for UB, LAMBDA.ineqlin is for the linear
% inequalities, LAMBDA.eqlin is for the linear equalities,
% LAMBDA.ineqnonlin is for the nonlinear inequalities, and
% LAMBDA.eqnonlin is for the nonlinear equalities.
%
% See also OPTIMOPTIONS, OPTIMGET.
% Copyright 1990-2018 The MathWorks, Inc.
% ---------------------More Details---------------------------
% [x]=fgoalattain(F,x,GOAL,WEIGHT,[],[],[],[],[],[],[],OPTIONS)
% Solves the goal attainment problem where:
%
% X Is a set of design parameters which can be varied.
% F Is a set of objectives which are dependent on X.
% GOAL Set of design goals. The optimizer will try to make
% F<GOAL, F=GOAL, or F>GOAL depending on the formulation.
% WEIGHT Set of weighting parameters which determine the
% relative under or over achievement of the objectives.
% Notes:
% 1.Setting WEIGHT=abs(GOAL) will try to make the objectives
% less than the goals resulting in roughly the same
% percentage under or over achievement of the goals.
% Note: use WEIGHT 1 for GOALS that are 0 (see Note 3 below).
% 2. Setting WEIGHT=-abs(GOAL) will try to make the objectives
% greater then the goals resulting in roughly the same percentage
% under- or over-achievement in the goals.
% Note: use WEIGHT 1 for GOALS that are 0 (see Note 3 below).
% 3. Setting WEIGHT(i)=0 indicates a hard constraint.
% i.e. F<=GOAL.
% OPTIONS.GoalsExactAchieve indicates the number of objectives for which it is
% required for the objectives (F) to equal the goals (GOAL).
% Such objectives should be partitioned into the first few
% elements of F.
% The remaining parameters determine tolerance settings.
%
%
%
defaultopt = struct( ...
'Diagnostics','off', ...
'DiffMaxChange',Inf, ...
'DiffMinChange',0, ...
'Display','final', ...
'FinDiffRelStep', [], ...
'FinDiffType','forward', ...
'FunValCheck','off', ...
'GoalsExactAchieve',0, ...
'GradConstr','off', ...
'GradObj','off', ...
'Hessian','off', ...
'LargeScale','off', ...
'MaxFunEvals','100*numberOfVariables', ...
'MaxIter',400, ...
'MaxSQPIter','10*max(numberOfVariables,numberOfInequalities+numberOfBounds)', ...
'MeritFunction','multiobj', ...
'OutputFcn',[], ...
'PlotFcns',[], ...
'RelLineSrchBnd',[], ...
'RelLineSrchBndDuration',1, ...
'TolCon',1e-6, ...
'TolConSQP',1e-6, ...
'TolFun',1e-6, ...
'TolFunValue',1e-6, ...
'TolX',1e-6, ...
'TypicalX','ones(numberOfVariables,1)', ...
'UseParallel',false ...
);
% If just 'defaults' passed in, return the default options in X
if nargin==1 && nargout <= 1 && strcmpi(FUN,'defaults')
x = defaultopt;
return
end
if nargin < 12
options = [];
if nargin < 11
NONLCON = [];
if nargin < 10
UB = [];
if nargin < 9
LB = [];
if nargin < 8
Beq = [];
if nargin < 7
Aeq = [];
if nargin < 6
B = [];
if nargin < 5
A = [];
end
end
end
end
end
end
end
end
algAS = 'active-set';
% Detect problem structure input
problemInput = false;
if nargin == 1
if isa(FUN,'struct')
problemInput = true;
[FUN,x,GOAL,WEIGHT,A,B,Aeq,Beq,LB,UB,NONLCON,options] = separateOptimStruct(FUN);
else % Single input and non-structure.
error(message('optim:fgoalattain:InputArg'));
end
end
% No options passed. Set options directly to defaultopt after
allDefaultOpts = isempty(options);
% Prepare the options for the solver
options = prepareOptionsForSolver(options, 'fgoalattain');
if nargin < 4 && ~problemInput
error(message('optim:fgoalattain:NotEnoughInputs'))
end
% Check for non-double inputs
msg = isoptimargdbl('FGOALATTAIN', {'X0','GOAL','WEIGHT','A','B','Aeq','Beq','LB','UB'}, ...
x, GOAL, WEIGHT, A, B, Aeq, Beq, LB, UB);
if ~isempty(msg)
error('optim:fgoalattain:NonDoubleInput',msg);
end
% Check for complex X0
if ~isreal(x)
error('optim:fgoalattain:ComplexX0', ...
getString(message('optimlib:commonMsgs:ComplexX0','Fgoalattain')));
end
% Set options to default if no options were passed.
if allDefaultOpts
% Options are all default
options = defaultopt;
end
initVals.xOrigShape = x;
sizes.xShape = size(x);
xnew = [x(:); 0];
numberOfVariablesplus1 = length(xnew);
sizes.nVar = numberOfVariablesplus1 - 1;
WEIGHT = WEIGHT(:);
GOAL = GOAL(:);
diagnostics = strcmpi(optimget(options,'Diagnostics',defaultopt,'fast',allDefaultOpts),'on');
display = optimget(options,'Display',defaultopt,'fast',allDefaultOpts);
flags.detailedExitMsg = contains(display,'detailed');
switch display
case {'off','none'}
verbosity = 0;
case {'notify','notify-detailed'}
verbosity = 1;
case {'final','final-detailed'}
verbosity = 2;
case {'iter','iter-detailed'}
verbosity = 3;
otherwise
verbosity = 2;
end
% Set to column vectors
B = B(:);
Beq = Beq(:);
[xnew(1:sizes.nVar),l,u,msg] = checkbounds(xnew(1:sizes.nVar),LB,UB,sizes.nVar);
if ~isempty(msg)
EXITFLAG = -2;
[FVAL,ATTAINFACTOR,LAMBDA] = deal([]);
OUTPUT.iterations = 0;
OUTPUT.funcCount = 0;
OUTPUT.stepsize = [];
OUTPUT.lssteplength = [];
OUTPUT.algorithm = algAS;
OUTPUT.firstorderopt = [];
OUTPUT.constrviolation = [];
OUTPUT.message = msg;
x(:) = xnew(1:sizes.nVar);
if verbosity > 0
disp(msg)
end
return
end
neqgoals = optimget(options, 'GoalsExactAchieve',defaultopt,'fast',allDefaultOpts);
% flags.meritFunction is 1 unless changed by user to fmincon merit function;
% formerly options(7)
% 0 uses the fmincon single-objective merit and Hess; 1 is the default
flags.meritFunction = strcmp(optimget(options,'MeritFunction',defaultopt,'fast',allDefaultOpts),'multiobj');
lenVarIn = length(varargin);
% goalcon and goalfun also take:
% neqgoals,funfcn,gradfcn,WEIGHT,GOAL,x,errCheck
goalargs = 7;
funValCheck = strcmp(optimget(options,'FunValCheck',defaultopt,'fast',allDefaultOpts),'on');
% Gather options needed for finitedifferences
% Write checked DiffMaxChange, DiffMinChage, FinDiffType, FinDiffRelStep,
% GradObj and GradConstr options back into struct for later use
options.FinDiffType = optimget(options,'FinDiffType',defaultopt,'fast',allDefaultOpts);
options.DiffMinChange = optimget(options,'DiffMinChange',defaultopt,'fast',allDefaultOpts);
options.DiffMaxChange = optimget(options,'DiffMaxChange',defaultopt,'fast',allDefaultOpts);
if options.DiffMinChange >= options.DiffMaxChange
error(message('optim:fgoalattain:DiffChangesInconsistent', sprintf( '%0.5g', options.DiffMinChange ), sprintf( '%0.5g', options.DiffMaxChange )))
end
% Read in and error check option TypicalX
[typicalx,ME] = getNumericOrStringFieldValue('TypicalX','ones(numberOfVariables,1)', ...
ones(sizes.nVar,1),'a numeric value',options,defaultopt);
if ~isempty(ME)
throw(ME)
end
checkoptionsize('TypicalX', size(typicalx), sizes.nVar);
options.TypicalX = typicalx(:);
options = validateFinDiffRelStep(sizes.nVar,options,defaultopt);
options.GradObj = optimget(options,'GradObj',defaultopt,'fast',allDefaultOpts);
options.GradConstr = optimget(options,'GradConstr',defaultopt,'fast',allDefaultOpts);
flags.grad = strcmp(options.GradObj,'on');
flags.gradconst = strcmp(options.GradConstr,'on');
if strcmpi(optimget(options,'Hessian',defaultopt,'fast',allDefaultOpts),'on')
warning(message('optim:fgoalattain:UserHessNotUsed'))
end
flags.hess = false;
constflag = ~isempty(NONLCON);
% If nonlinear constraints exist, need either both function and constraint
% gradients, or none
if constflag
flags.gradconst = flags.grad && flags.gradconst;
else % No user nonlinear constraints
flags.gradconst = flags.grad;
end
flags.grad = true; % Always can compute gradient of goalfun since based on x
% Update options GradObj and GradConstr to reflect the update for the
% constraint function
if ~flags.gradconst
options.GradObj = 'off';
options.GradConstr = 'off';
end
% if we have a string object input, we need to convert to char arrays
if isstring(FUN)
if isscalar(FUN)
FUN = char(FUN);
else
FUN = cellstr(FUN);
end
end
% Convert to inline function as needed
% FUN is called from goalcon; goalfun is based only on x
if ~isempty(FUN) % will detect empty string, empty matrix, empty cell array
% Pass flags.gradconst as the flag which tells whether or not to
% evaluate gradients from the user function. flags.grad is meant for
% goalfun and is always set to true for this problem.
funfcn = optimfcnchk(FUN,'goalcon',length(varargin),funValCheck, ...
flags.gradconst,flags.hess);
else
error(message('optim:fgoalattain:InvalidFUN'))
end
if constflag % NONLCON is non-empty
confcn = optimfcnchk(NONLCON,'goalcon',length(varargin),funValCheck, ...
flags.gradconst,false,true);
else
confcn{1} = '';
end
% Pass in false for funValCheck argument as goalfun/goalcon is not a user function
ffun = optimfcnchk(@goalfun,'fgoalattain',lenVarIn+goalargs,false,flags.grad);
cfun = optimfcnchk(@goalcon,'fgoalattain',lenVarIn+goalargs,false,flags.gradconst,false,true);
lenvlb = length(l);
lenvub = length(u);
i = 1:lenvlb;
lindex = xnew(i) < l(i);
if any(lindex)
xnew(lindex) = l(lindex) + 1e-4;
end
i = 1:lenvub;
uindex = xnew(i) > u(i);
if any(uindex)
xnew(uindex) = u(uindex);
end
x(:) = xnew(1:end-1);
sizes.nFun = length(GOAL); % Assume the length of GOAL is same as length
% of user function; we will verify this later.
% Check if neqgoals (GoalsExactAchieve) is less or equal to the length of user function
if neqgoals > sizes.nFun
warning(message('optim:fgoalattain:InconsistentNumEqGoal'))
% The number of goals to be achieved exactly can be at most equal to the
% length of user objective function.
neqgoals = sizes.nFun;
end
if length(WEIGHT) ~= length(GOAL)
error(message('optim:fgoalattain:InvalidWeightAndGoalSizes'))
end
initVals.g = zeros(numberOfVariablesplus1,1);
initVals.H = [];
errCheck = true; % Perform error checking on initial function evaluations
extravarargin = [{neqgoals,funfcn,confcn,WEIGHT,GOAL,x,errCheck}, varargin];
% Evaluate goal function
switch ffun{1}
case 'fun'
initVals.f = feval(ffun{3},xnew,extravarargin{:});
case 'fungrad'
[initVals.f,initVals.g] = feval(ffun{3},xnew,extravarargin{:});
otherwise
error(message('optim:fgoalattain:InvalidCalltype'))
end
% Evaluate goal constraints
switch cfun{1}
case 'fun'
[ctmp,ceqtmp] = feval(cfun{3},xnew,extravarargin{:});
initVals.ncineq = ctmp(:);
initVals.nceq = ceqtmp(:);
initVals.gnc = zeros(numberOfVariablesplus1,length(initVals.ncineq));
initVals.gnceq = zeros(numberOfVariablesplus1,length(initVals.nceq));
case 'fungrad'
[ctmp,ceqtmp,initVals.gnc,initVals.gnceq] = feval(cfun{3},xnew,extravarargin{:});
initVals.ncineq = ctmp(:);
initVals.nceq = ceqtmp(:);
otherwise
error(message('optim:fgoalattain:InvalidCalltype'))
end
% Make sure empty constraint and their derivatives have correct sizes (not 0-by-0):
if isempty(initVals.ncineq)
initVals.ncineq = reshape(initVals.ncineq,0,1);
end
if isempty(initVals.nceq)
initVals.nceq = reshape(initVals.nceq,0,1);
end
if isempty(Aeq)
Aeq = reshape(Aeq,0,sizes.nVar);
Beq = reshape(Beq,0,1);
end
if isempty(A)
A = reshape(A,0,sizes.nVar);
B = reshape(B,0,1);
end
sizes.mNonlinEq = length(initVals.nceq);
sizes.mNonlinIneq = length(initVals.ncineq);
[lin_eq,Aeqcol] = size(Aeq);
[lin_ineq,Acol] = size(A);
if Aeqcol ~= sizes.nVar
error(message('optim:fgoalattain:InvalidSizeOfAeq', sizes.nVar))
end
if Acol ~= sizes.nVar
error(message('optim:fgoalattain:InvalidSizeOfA', sizes.nVar))
end
just_user_constraints = sizes.mNonlinIneq - sizes.nFun - neqgoals;
OUTPUT.algorithm = algAS;
if diagnostics
% Do diagnostics on information so far
diagnose('fgoalattain',OUTPUT,flags.gradconst,flags.hess,constflag,flags.gradconst,...
xnew(1:end-1),sizes.mNonlinEq,just_user_constraints,lin_eq,lin_ineq,LB,UB,funfcn,confcn);
end
% Add extra column to account for extra xnew component
A = [A,zeros(lin_ineq,1)];
Aeq = [Aeq,zeros(lin_eq,1)];
% Only need to perform error checking on initial function evaluations
errCheck = false;
% Convert function handles to anonymous functions with additional arguments
% in its workspace. Even though ffun and cfun are internal functions, put fevals
% here for consistency.
ffun{3} = @(y,varargin) feval(ffun{3},y,neqgoals,funfcn,confcn,WEIGHT,GOAL,x,errCheck,varargin{:});
cfun{3} = @(y,varargin) feval(cfun{3},y,neqgoals,funfcn,confcn,WEIGHT,GOAL,x,errCheck,varargin{:});
% Problem related data is passed to nlconst in problemInfo structure
problemInfo.nHardConstraints = neqgoals;
problemInfo.weight = WEIGHT;
problemInfo.goal = GOAL;
% Create default structure of flags for finitedifferences:
% This structure will (temporarily) ignore some of the features that are
% algorithm-specific (e.g. scaling and fault-tolerance) and can be turned
% on later for the main algorithm.
finDiffFlags.fwdFinDiff = strcmpi(options.FinDiffType,'forward');
finDiffFlags.scaleObjConstr = false; % No scaling for now
finDiffFlags.chkFunEval = false; % No fault-tolerance yet
finDiffFlags.chkComplexObj = false; % No need to check for complex values
finDiffFlags.isGrad = false; % Multi-objective
finDiffFlags.hasLBs = false(sizes.nVar,1);
finDiffFlags.hasUBs = false(sizes.nVar,1);
if ~isempty(l)
finDiffFlags.hasLBs = isfinite(l); % Finite lower bounds
end
if ~isempty(u)
finDiffFlags.hasUBs = isfinite(u); % Finite upper bounds
end
% Adjust nVar-length vectors used by finite-differencing for auxiliary variable
options.TypicalX = [typicalx(:); 1]; % add element for auxiliary variable
if finDiffFlags.fwdFinDiff
options.FinDiffRelStep = [options.FinDiffRelStep; sqrt(eps)];
else
options.FinDiffRelStep = [options.FinDiffRelStep; eps^(1/3)];
end
l = [l;-Inf];
u = [u; Inf];
finDiffFlags.hasLBs = [finDiffFlags.hasLBs; false];
finDiffFlags.hasUBs = [finDiffFlags.hasUBs; false];
finDiffFlags.isGrad = true; % New formulation has single objective
% For parallel finite difference (if needed) we need to send the function
% handles now to the workers. This avoids sending the function handles in
% every iteration of the solver. The output from 'setOptimFcnHandleOnWorkers'
% is a onCleanup object that will perform cleanup task on the workers.
UseParallel = optimget(options,'UseParallel',defaultopt,'fast',allDefaultOpts);
cleanupObj = setOptimFcnHandleOnWorkers(UseParallel,ffun,cfun); %#ok<NASGU>
% Flag to determine whether to look up the exit msg.
flags.makeExitMsg = logical(verbosity) || nargout > 4;
[xnew,ATTAINFACTOR,LAMBDA,EXITFLAG,OUTPUT]=...
nlconst(ffun,xnew,l,u,full(A),B,full(Aeq),Beq,cfun,options,defaultopt, ...
finDiffFlags,verbosity,flags,initVals,problemInfo,varargin{:});
if ~isempty(LAMBDA)
just_user_constraints = length(LAMBDA.ineqnonlin) - sizes.nFun - neqgoals;
LAMBDA.ineqnonlin = LAMBDA.ineqnonlin(1:just_user_constraints);
LAMBDA.lower = LAMBDA.lower(1:sizes.nVar);
LAMBDA.upper = LAMBDA.upper(1:sizes.nVar);
end
% Evaluate user objective functions
x(:) = xnew(1:end-1);
FVAL = feval(funfcn{3},x,varargin{:});
% Force a cleanup of the handle object. Sometimes, MATLAB may
% delay the cleanup but we want to be sure it is cleaned up.
clear cleanupObj
3.运行结果