•  🍨 本文为🔗365天深度学习训练营 中的学习记录博客
• 🍖 原作者：K同学啊

我的环境：

• 语言环境：Python3.10.7
• 编译器：VScode
• 深度学习环境：TensorFlow 2.13.0

一、前期工作： 

1、导入数据集

import tensorflow as tf
import pandas     as pd
import numpy      as np


df_1 = pd.read_csv("D:/R2woodpine2.csv")
print(df_1.head())

 

import matplotlib.pyplot as plt
import seaborn as sns

plt.rcParams['savefig.dpi'] = 500 #图片存储像素
plt.rcParams['figure.dpi']  = 100 #图片显示分辨率
fig, ax =plt.subplots(1,3,constrained_layout=True, figsize=(14, 3))
sns.lineplot(data=df_1["Tem1"], ax=ax[0])
sns.lineplot(data=df_1["CO 1"], ax=ax[1])
sns.lineplot(data=df_1["Soot 1"], ax=ax[2])
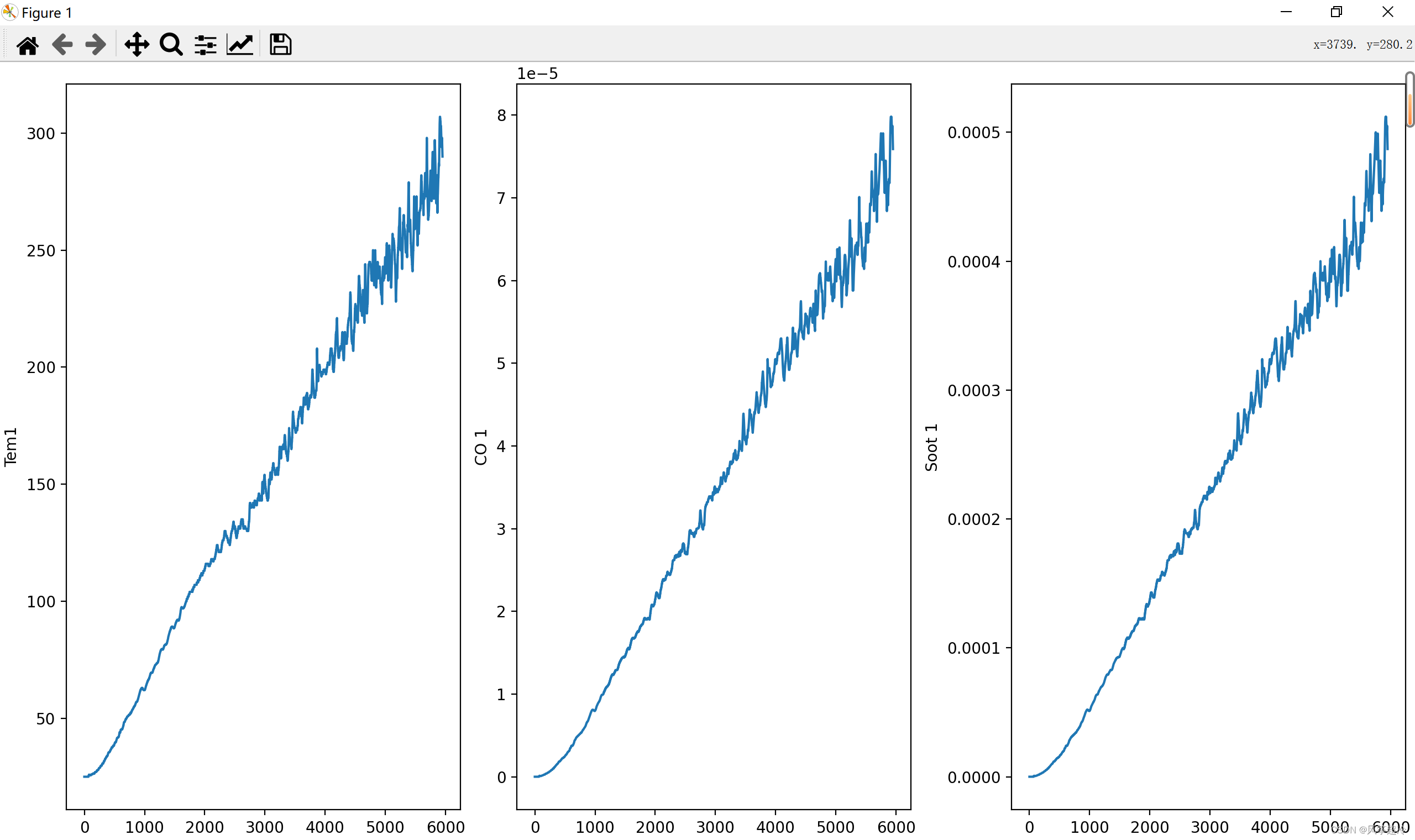
plt.show()

代码使用matplotlib和seaborn库创建了三个并排的折线图。

1. `plt.rcParams['savefig.dpi'] = 500`：这行代码设置保存图像时的分辨率，即每英寸的像素数。如果你将绘制的图像保存为图片文件（比如PNG格式），它的分辨率将是500 DPI。

2. `plt.rcParams['figure.dpi'] = 500`：这行代码设置绘制图像时的分辨率，默认情况下图像在屏幕或笔记本中显示的效果。较高的分辨率值会使图像显示更加清晰和细节丰富。

3. `fig, ax = plt.subplots(1, 3, constrained_layout=True, figsize=(14, 3))`：创建一个图形对象和三个子图（坐标轴），子图按照一行三列的方式排列。`fig` 是图形对象，`ax` 是一个包含三个子图坐标轴的数组，每个子图用于显示一个折线图。`constrained_layout=True`选项确保子图之间的间距合适，不会重叠。

4. `sns.lineplot(data=df_1["Tem1"], ax=ax[0])`：创建"Tem1"列的折线图，数据来自DataFrame `df_1`。折线图被放置在第一个子图（`ax[0]`）中。`sns.lineplot`是seaborn库中简化绘制折线图的函数。

5. `sns.lineplot(data=df_1["CO 1"], ax=ax[1])`：创建"CO 1"列的折线图，数据同样来自DataFrame `df_1`。折线图被放置在第二个子图（`ax[1]`）中。

6. `sns.lineplot(data=df_1["Soot 1"], ax=ax[2])`：这行代码创建了"Soot 1"列的折线图，数据同样来自DataFrame `df_1`。折线图被放置在第三个子图（`ax[2]`）中。

二、构建数据集 

dataFrame=df_1.iloc[:,1:]
print(dataFrame.head())

`dataFrame=df_1.iloc[:,1:]` 是从 `df_1` DataFrame 中选取所有行和从第二列开始的所有列，然后将结果赋值给一个新的 DataFrame 变量 `dataFrame`。

 

设置xy，取前8个时间段的Tem1、CO 1、Soot 1为X，第9,10个时间段的Tem1为y。

width_X=8
width_y=2

X = []
y = []

in_start = 0

for _, _ in df_1.iterrows():
    in_end  = in_start + width_X
    out_end = in_end   + width_y
    
    if out_end < len(dataFrame):
        X_ = np.array(dataFrame.iloc[in_start:in_end , ])
        
        X_ = X_.reshape((len(X_)*3))#3根据自变量数目而定
        y_ = np.array(dataFrame.iloc[in_end  :out_end, 0])
        
        X.append(X_)
        y.append(y_)
    
    in_start += 1

X = np.array(X)
y = np.array(y)

X.shape, y.shape

for _, _ in df_1.iterrows():: 这是一个循环，遍历了 df_1 中的每一行数据。但是在代码中并没有使用循环中的变量 _，这意味着这个循环仅仅用于迭代，而没有在循环体内使用行的具体数据。

归一化

#将数据归一化
sc       = MinMaxScaler(feature_range=(0, 1))
X_scaled = sc.fit_transform(X)
print(X_scaled.shape)
#
X_scaled=X_scaled.reshape(len(X_scaled),width_X,3)
print(X_scaled.shape)

1. print(X_scaled.shape): 这行代码打印出 X_scaled 数组的形状。X_scaled 是缩放后的特征矩阵，其形状为 (样本数, 特征数)。

2. X_scaled = X_scaled.reshape(len(X_scaled), width_X, 3): 这行代码对 X_scaled 进行了 reshape 操作。reshape 函数用于改变数组的形状。在这里，将 X_scaled 数组的形状改为 (样本数, width_X, 3)。width_X 是输入窗口的宽度，而 3 是每个时间步包含的特征数。

 

划分数据集（前5000条数据为训练集，5000条之后为验证集）

X_train=X_scaled[:5000]
y_train=y[:5000]
X_test=X_scaled[5000:,]
y_test=y[5000:,]
print("训练集和验证集划分")
print("X_train：",X_train.shape)
print("y_train:",y_train.shape)
print("X_test:",X_test.shape)
print("y_test:",y_test.shape)

 三、使用 TensorFlow 中的 Keras API 来构建一个 LSTM（长短期记忆网络）模型

这段代码构建了一个 LSTM 模型，其中包含两个 LSTM 层和一个 Dense 输出层。LSTM 层用于处理时间序列数据，`return_sequences=True` 设置确保中间的 LSTM 层输出也是一个时间序列，而不仅仅是最后一个时间步的输出。最后的 Dense 层输出预测目标的结果。

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense,LSTM,Bidirectional
from tensorflow.keras        import Input

model_lstm = Sequential()
model_lstm.add(LSTM(units=64, activation='relu', return_sequences=True,
               input_shape=(X_train.shape[1], 3)))
model_lstm.add(LSTM(units=64, activation='relu'))

model_lstm.add(Dense(width_y))

1. `from tensorflow.keras.models import Sequential`: 导入 Keras 中的 Sequential 模型类，它允许我们按照顺序将各种层叠加起来构建神经网络。

2. `from tensorflow.keras.layers import Dense, LSTM, Bidirectional`: 导入 Keras 中的 Dense 层（全连接层）、LSTM 层（长短期记忆层）和 Bidirectional 层（双向 LSTM 层）。

3. `from tensorflow.keras import Input`: 导入 Keras 中的 Input 类，用于指定输入数据的形状。

4. `model_lstm = Sequential()`: 创建一个空的 Sequential 模型对象 `model_lstm`。

5. `model_lstm.add(LSTM(units=64, activation='relu', return_sequences=True, input_shape=(X_train.shape[1], 3)))`: 向模型中添加一个 LSTM 层。

   - `units=64`: 表示 LSTM 层中有 64 个神经元。
   - `activation='relu'`: 表示 LSTM 层使用 ReLU（Rectified Linear Unit）激活函数。
   - `return_sequences=True`: 表示 LSTM 层的输出将作为下一个 LSTM 层的输入，而不是仅返回最后一个时间步的输出。
   - `input_shape=(X_train.shape[1], 3)`: 指定输入数据的形状。`X_train` 是输入数据的训练集，它的形状为 `(样本数, 时间步数, 特征数)`，在这里 `X_train.shape[1]` 表示时间步数，而 `3` 表示每个时间步的特征数。

6. `model_lstm.add(LSTM(units=64, activation='relu'))`: 向模型中再添加一个 LSTM 层。

   - `units=64`: 表示 LSTM 层中有 64 个神经元。
   - `activation='relu'`: 表示 LSTM 层使用 ReLU（Rectified Linear Unit）激活函数。

7. `model_lstm.add(Dense(width_y))`: 向模型中添加一个 Dense 层。

   - `width_y`: 这是一个之前定义的变量，表示预测目标的宽度，也就是需要预测的时间步数。
   - 这个 Dense 层用于输出最终的预测结果，因此它的神经元数等于 `width_y`，并且没有指定激活函数，即默认为线性激活函数。

四、模型编译

#只观察loss数值，不观察准确率，所以删去metrics选项
model_lstm.compile(optimizer=tf.keras.optimizers.Adam(1e-3),
                  loss='mean_squared_error')
from tensorflow.keras.callbacks import ModelCheckpoint
ModelCheckPointer=ModelCheckpoint('best_model.h5',
                                  monitor='val_loss',
                                  save_best_only=True,
                                  save_weights_only=True,               
                )

history_lstm=model_lstm.fit(X_train,y_train,
                            batch_size=64,
                            epochs=50,
                            validation_data=(X_test,y_test),
                            validation_freq=1,
                            callbacks=[ModelCheckPointer])

五、loss评估 

# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

plt.figure(figsize=(5, 3),dpi=120)

plt.plot(history_lstm.history['loss']    , label='LSTM Training Loss')
plt.plot(history_lstm.history['val_loss'], label='LSTM Validation Loss')

plt.title('Training and Validation Loss')
plt.legend()
plt.show()

六、预测 

import tensorflow as tf
import pandas     as pd
import numpy      as np
import matplotlib.pyplot as plt
import seaborn as sns

df_1 = pd.read_csv("D:/R2woodpine2.csv")

dataFrame=df_1.iloc[:,1:]


width_X=8
width_y=2

X = []
y = []

in_start = 0

for _, _ in df_1.iterrows():
    in_end  = in_start + width_X
    out_end = in_end   + width_y
    
    if out_end < len(dataFrame):
        X_ = np.array(dataFrame.iloc[in_start:in_end , ])
        X_ = X_.reshape((len(X_)*3))
        y_ = np.array(dataFrame.iloc[in_end  :out_end, 0])
        X.append(X_)
        y.append(y_)
    
    in_start += 1
X = np.array(X)
y = np.array(y)


from sklearn.preprocessing import MinMaxScaler

#将数据归一化，
print("归一化中……")
sc       = MinMaxScaler(feature_range=(0, 1))
X_scaled = sc.fit_transform(X)
X_scaled=X_scaled.reshape(len(X_scaled),width_X,3)
print("归一化完成！")

X_train=X_scaled[:5000]
y_train=y[:5000]
X_test=X_scaled[5000:,]
y_test=y[5000:,]
print("训练集和验证集划分")
print("X_train：",X_train.shape)
print("y_train:",y_train.shape)
print("X_test:",X_test.shape)
print("y_test:",y_test.shape)

print("构建网络完成")
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense,LSTM,Bidirectional
from tensorflow.keras        import Input

model_lstm = Sequential()
model_lstm.add(LSTM(units=64, activation='relu', return_sequences=True,
               input_shape=(X_train.shape[1], 3)))
model_lstm.add(LSTM(units=64, activation='relu'))
model_lstm.add(Dense(width_y))

#只观察loss数值，不观察准确率，所以删去metrics选项
'''model_lstm.compile(optimizer=tf.keras.optimizers.Adam(1e-3),
                  loss='mean_squared_error')
from tensorflow.keras.callbacks import ModelCheckpoint
ModelCheckPointer=ModelCheckpoint('best_model.h5',
                                  monitor='val_loss',
                                  save_best_only=True,
                                  save_weights_only=True,               
                )

history_lstm=model_lstm.fit(X_train,y_train,
                            batch_size=64,
                            epochs=50,
                            validation_data=(X_test,y_test),
                            validation_freq=1,
                            callbacks=[ModelCheckPointer])

print("编译完成")


# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.figure(figsize=(5, 3),dpi=120)
plt.plot(history_lstm.history['loss']    , label='LSTM Training Loss')
plt.plot(history_lstm.history['val_loss'], label='LSTM Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()'''

#预测
predicted_y_lstm = model_lstm.predict(X_test)                        # 测试集输入模型进行预测 
y_test_one = [i[0] for i in y_test]
predicted_y_lstm_one = [i[0] for i in predicted_y_lstm]
plt.figure(figsize=(5, 3),dpi=120)
# 画出真实数据和预测数据的对比曲线
plt.plot(y_test_one[:2000], color='red', label='真实值')
plt.plot(predicted_y_lstm_one[:2000], color='blue', label='预测值')
 
plt.title('Title')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()

from sklearn import metrics
"""
RMSE ：均方根误差,对均方误差开方
R2   ：决定系数，可以简单理解为反映模型拟合优度的重要的统计量
"""
RMSE_lstm  = metrics.mean_squared_error(predicted_y_lstm, y_test)**0.5
R2_lstm    = metrics.r2_score(predicted_y_lstm, y_test)
print('均方根误差: %.5f' % RMSE_lstm)
print('R2: %.5f' % R2_lstm)