前言

今天的干货来了，十字相乘。

十字相乘

研究对象

普通二次三项式和二次齐次式

类型

普通二次三项式

基本形式

$a{x}^2+bx+c(a\ne 0)$

分解步骤

1. 将 $a{x}^2+bx+c$ 理顺。
2. 把 $a{x}^2$、 $bx$、$c$ 拆开看
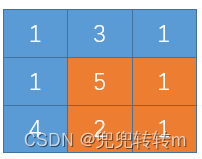
3. 把二次项和常数项各拆成两个因数的积，如下图排列：
   
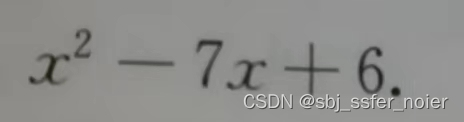
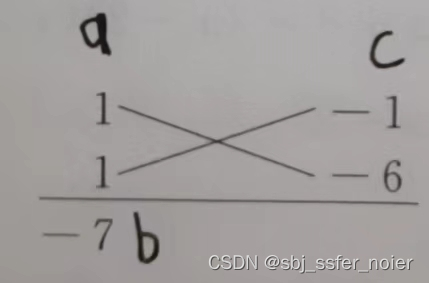
4. 将2条对角线的数相连再乘起来得到2个积求和
5. 如果得到的和与b相等，则跳到6，否则跳到4
6. 看示例第一行分别是 1 -1 就写成$(x-1)$,第二行分别是 1 -6 就写成$(x-6)$
7. 最终效果就是$(x-1)(x-6)$

注意

1. 此示例举得是a为正的情况，当a为负时，先提取$-1$作为公因数
2. 若步骤③不成立时，再做一次步骤③。

二次齐次式

基本形式

$a{x}^2+bxy+c{y}^2(a\ne 0，c\ne 0)$

分组步骤

1. 将 $a{x}^2+bxy+c{y}^2$ 理顺。
2. 把 $a{x}^2$、 $bxy$、$c{y}^2$ 拆开看
3. 把ax² 和 cy²各拆成两个因数的积，如下图排列：
   
   
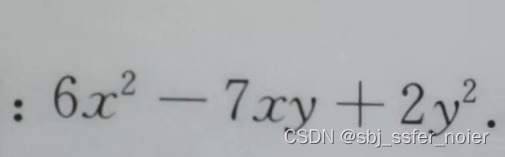
4. 将2条对角线的数相连再乘起来得到2个积求和
5. 如果得到的和与b相等，则跳到6，否则跳到4
6. 看示例第一行分别是 2 -1 就写成$(2x-y)$,第二行分别是 3 -2 就写成$(3x-2y)$
7. 最终效果就是$(2x-y)(3x-2y)$

注意

千万不要忘记还有一个$y$

系数和为0的普通二次三项式

这个是一个特例，只要熟练掌握了上2个方法，这个听听就完了。

普通二次三项式 $a{x}^2+bx+c$
∵ $a+b+c=0$
∴$a{x}^2+bx+c=(x-1)(ax-c)$

根本上是因为 $b=-(a+c)$

习题5

题目

题解