NLG解码策略
自然语言生成(Natural Language Generation,简称NLG),是自然语言处理领域的一个重要分支,在文本摘要生成任务中,另一个重要的分支是自然语言理解(Natural Language Understanding,简称NLU)。前面我们已经学习了seq2seq模型结构,其主要分为Encoder和Decoder两大组件,其实正是对应了NLU和NLG两大分支,seq2seq模型最后经过一个softmax层,在每个时间步均得到一个词表大小的概率分布,如何利用这些概率分布得到最终的预测句子就是本节学习的解码策略。
上篇构建文本摘要baseline时,我们就有提到过解码方法,当时采用的Teacher forcing的技巧,使用了真实标签,避免前面的步骤预测出错被无限放大的问题,但是在实际预测时因为没有真实标签,往往实际预测效果不一定好,所以寻找可行的解码策略是一项重点工作。
暴力解法
seq2seq模型最后经过一个softmax层,在每个时间步均得到一个词表大小的概率分布,但是这些时间步的概率分布并非同一时间得到的,后面时间步的概率分布生成受前面时间步的概率分布的影响,还记得在seq2seq模型中decoder部分,上一时间步的输出会作为输入的一部分进入下一个时间步,所以并不是说直接取每个时间步概率最大的词就得到了最佳的预测结果(虽然greedy search是这样做的)。这种情况下,我们常想到的办法就是把每个时间步,每个预测词都作为一种可能性,然后不断地去生成后面的词,最终计算每个句子总概率值(分值score),选择概率最大的作为预测结果。

这种方法也是我们刷Leetcode,没有好的方法时常采用的暴力解法,缺点就是时间复杂度太高,就像这里,每个时间步有V种可能性(V表示词表大小),一共T个时间步,总共有V的T次方种可能性,计算量太大,可行性差。
Greedy Search

greedy search的想法就比较简单了,也就是我上面说的,直接选取每个时间步的最大概率的词,但是有个缺点就是前面的选错了会影响后面的,导致错误被一直传递下去,但是依然是一种简单可行的方法,下面通过一段模拟模型生成的代码来实现greedy search。
import numpy as np
import matplotlib.pyplot as plt
# 定义词典(就是26个英文字母)
dictionary = []
for c in range(ord('a'), ord('z')+1):
dictionary.append(chr(c))
print(f'词典:{dictionary}')
# 模拟一个已经被训练好的LM
class LanguageModel:
def __init__(self, dictionary):
self.dictionary = dictionary
def predict(self):
output = np.random.rand(len(dictionary))
output = output/output.sum()
return output
model = LanguageModel(dictionary)
predictions = model.predict()
plt.bar(dictionary, predictions)
plt.show()
def greedy_search(conditional_probability):
return np.argmax(conditional_probability)
next_token = greedy_search(predictions)
print("sample token: ", dictionary[next_token])
输出:
词典:['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']
sample token: w
当模型生成<END>标志时,通常表示解码结束。
Beam Search
greedy search中因为只选取一个最大的概率词,那么生成的结果会比较单一,为了让生成的结果更多样性,基于greedy search有一种更好的方法就是在每个时间步选取概率分布最大的n个词(n值一般取5~10),俗称top-n(注意与后续的top-k sampling做区分)。
Beam search的具体流程:



重复以上步骤,直至最终生成了k个句子,然后选取一个分数值最高的句子作为最终输出。

停止条件
其实与greedy search中类似,当模型在某个时间步输出<END>时,表示该假设已经结束,但是因为不同的假设的终止时间步可能不一致,所以当某个假设结束时,不会影响其他假设,其他假设会继续生成。
但是存在极低的可能性模型一直无法输出<END>,所以一般会设置超参-最大的时间步,也就是达到最大时间步后该假设自动终止;同样地,也会设置超参要生成多少个假设,生成的假设数量够了就不再生成新的假设。
代码实现
同样使用上面的模拟词典和模拟概率
def beam_search_decoder(data, k):
sequences = [[list(), 0.0]]
# 迭代序列中的每一步
for row in data:
all_candidates = list()
# 计算每种hypotheses的分值,并存储到all_candidates
for i in range(len(sequences)):
seq, score = sequences[i]
for j in range(len(row)):
candidate = [seq + [j], score - np.log(row[j])]
all_candidates.append(candidate)
# 对所有的候选序列,通过score排序
ordered = sorted(all_candidates, key=lambda tup: tup[1])
# 选择k个分score 最高的
sequences = ordered[:k]
return sequences
t = 10 # 总共10个时间步
data = []
for i in range(t):
prediction = model.predict()
data.append(prediction)
data = np.array(data)
result = beam_search_decoder(data, 5)
for seq in result:
print(seq)
[[13, 21, 16, 11, 20, 7, 14, 7, 16, 2], 25.78893247277384]
[[13, 21, 16, 11, 20, 7, 14, 16, 16, 2], 25.792550613854544]
[[21, 21, 16, 11, 20, 7, 14, 7, 16, 2], 25.792704168774012]
[[21, 21, 16, 11, 20, 7, 14, 16, 16, 2], 25.796322309854716]
[[13, 21, 16, 11, 20, 7, 14, 7, 11, 2], 25.81314273033993]
k的选择
当k是一个比较小的值时,生成的句子可能会不符合语法规则,不自然,无意义,不正确;
特殊地,当k=1时,变成greedy search
当k是一个比较大的值时,可以减少上述问题,但是会增加大量的运算;但是还有带来另外的问题:
- 对于机器翻译任务来说,如果k增大的过多,
BLEU score下降的特别快,主要是因为k越大,生成的句子会越短(句子短的会得分高); - 在闲聊对话系统中(chit-chat),越大的k约会偏离主题,虽然生成的句子确实会更通顺,(看下图)。

所以K的选取对结果影响很大,需要根据自己的任务进行实验。
Penalize longer sequences

观察分值score的计算公式,首先P是一个小于1的值,那么log§就是一个负值,所以我们会发现,生成的句子越长,得分就会越小,这明显不是我们期望看到的,可以通过以下两种方式解决。

其中第二种方法在这篇论文中被提出。
Repetitive Problem
在文本生成领域,重复生成的问题是一个非常常见的问题,有研究发现,当生成重复的句子时,损失值会不断减小,一般有以下三种方法来解决重复的问题:
-
通过写代码来控制模型减少生成重复词,刚开始可以尝试此种方法,锻炼编码能力;
-
更改loss,通过增加额外的损失来降低已生成句子(ht-m)和后续生成句子(ht)的相似度

- 不使用基于极大似然的损失函数,这篇论文中有详细描述

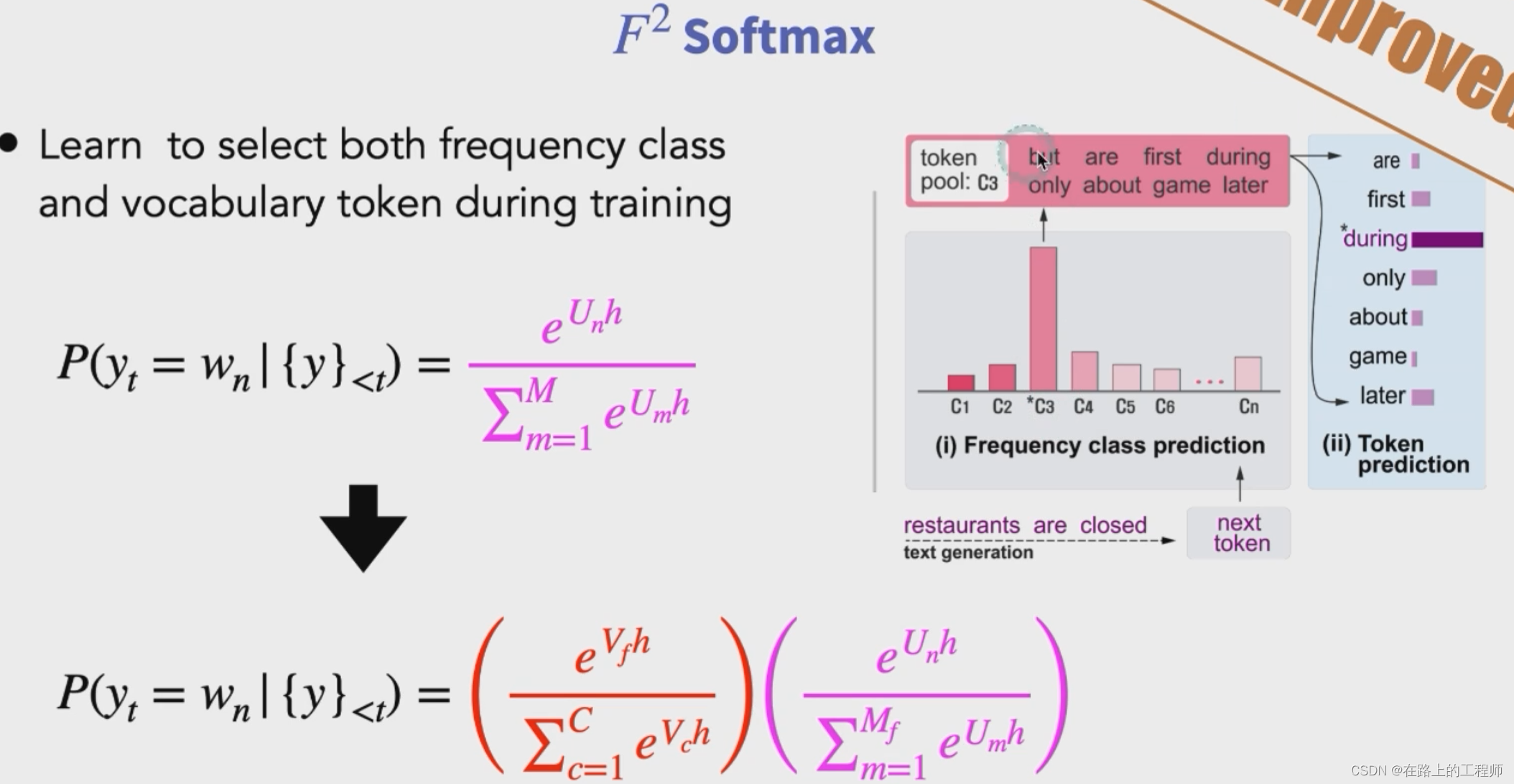
- F² softmax,源自这篇文章,主要是先根据频率将词表分组,然后使用两次softmax来选词,即先确定从哪一组选词,再确定选取该组中哪个词。