1 前言

1.1 题目描述

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

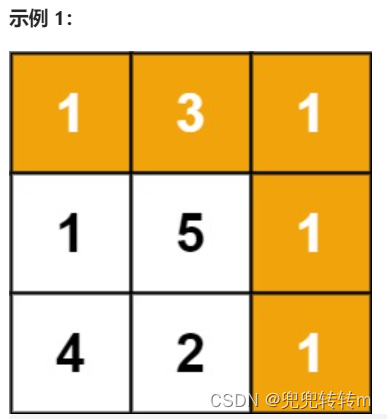
如下图所示：

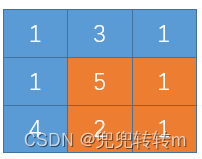
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7

 1.2 题目解析

看到这个题，首先想出来的是使用动态规划。

设置dp[i][j] 表示走到(i,j)节点的最小路径和。

此时我们要分三种情况。

第一种，上图二维数组中最上面的[1,3,1]，它只能从被其左侧前一个节点走到。

 

第二种，上图二维数组中最左侧的[1,1,4]，它只能被其上面一个节点走到。

 

第三种，是剩余部分，可以从其上侧节点或者左侧节点走到。

 

因此dp数组的更新策略也有三种

第一种：dp[0][j] = dp[0][j-1] + grid[0][j];

第二种：dp[i][0] = dp[i-1][0] + grid[i][0]

第三种：dp[i][j] = gird[i][j] +min(dp[i-1][j],dp[i][j-1])

1.3 代码实现

package cn.msf.hot100;

import java.util.Arrays;

/**
 * @author : msf
 * @date : 2022/12/12
 * 最小路径和
 */
public class MinPathSum {
    public static void main(String[] args) {
        int[][] grid = {{1,2,3},{4,5,6}};
        int result = new MinPathSum().minPathSum(grid);
        System.out.println(result);
    }


    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        // 处理顶层的行
        for (int i = 1; i < n; i++) {
            dp[0][i] = grid[0][i] + dp[0][i-1];
        }
        // 处理最左边的列
        for (int j = 1; j < m; j++) {
            dp[j][0] = grid[j][0] + dp[j-1][0];
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = grid[i][j] + Math.min(dp[i-1][j],dp[i][j-1]);
            }
        }

        return dp[m-1][n-1];
    }
}