前言:此题被分类到散列表算法题目中,但乍一看此题实在想不到如何去使用散列表,直到看了官方给的答案。。。。。。
题目描述:
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。

解题思路及代码:
思路1:HashSet解法:
在题目对快乐数的定义中已经给出了两种情况我们分别举例出来:
1.是快乐数,即最后循环到1(19 ->82 -> 68 -> 100 -> 1)
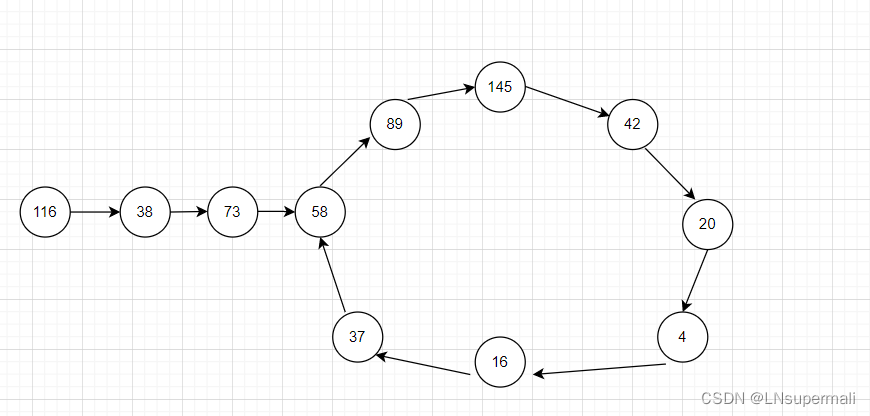
2.不是快乐数,循环过程中出现死循环(也可以理解为出现了一个环这也是想到使用类双指针方法的一个启示。)
我们第一眼凭直觉感觉还可能出现第三种情况:
3.循环的值越来越大,直至接近无穷大
若出现第三种情况我们编码将会变得很困难,因为我们怎么知道需要判断的数是会继续变大以至无穷大还是最终变为1?但是其实第三种情况是不存在在,此处就以力扣官方答案的证明为例(简洁明了)
| 位数 | 该位数最大的整数 | 最大数的下一位 |
|---|---|---|
| 1 | 9 | 81 |
| 2 | 99 | 162 |
| 3 | 999 | 243 |
| 4 | 9999 | 324 |
| 13 | 9999999999999 | 1053 |
我们们考虑不同位数的最大整数的下一位,三位最大整数位“999”,其下一位计算得到为“243”是一个三位数,当n为四位数时,最大整数“9999”的下一位为三位整数“324”,即说明四位数在循环的过程中要么会出现快乐数要么会在某个地方出现环,反正其最终也会下降至三位数或者继续下降位数,同理,比四位数高的数亦如此(也就是位数最终都不会超过一个最大的位数)!!!
接下来就是解答开篇的疑惑:如何或者为何使用哈希表,我们讲大问题主要分成以下两部分:
1.按照题目实现数位分离并求取平方和
2.每次生成链中的下一个数字时,我们都检查其是否在哈希表中;若不在则添加,若已经在了,则说明此时已经在一个环中,返回false。
所以我们选择哈希表就是便于将判断的时间复杂度降低!!!
代码:
class Solution {
public boolean isHappy(int n) {
HashSet<Integer> set = new HashSet<>();
while (n != 1 && !set.contains(n)) {
set.add(n);
n = getNext(n);
}
return n == 1;
}
private int getNext(int n) {
int totalSum = 0;
while (n > 0) {
int d = n % 10;
n = n / 10;
totalSum += d * d;
}
return totalSum;
}
}
思路二:类双指针法(快慢指针):
之所以叫做类快慢指针即不是正真意义的双指针,而是利用双指针的思想。由于我们在思路1已经发现若已经存在环则说明不是快乐数,那我们可以使用快慢指针思想去类比解决此问题(此处推荐去练习一下力扣141.环形链表也可以使用快慢指针解决)
每次调用两次getNext()方法实现快指针每次移动两步,调用一次getNext()方法实现慢指针的移动
检测快慢指针是否相等,相等则说明存在环
代码:
class Solution {
public boolean isHappy(int n) {
int slowRunner = n;
int fastRunner = getNext(n);
while (fastRunne != 1 && slowRunner != fasterRunner) {
slowRunner = getNext(slowRunner);
fastRunner = getNext(getNext(fastRunner));
}
return fastRunner == 1;
}
private int getNext(int n) {
int totalSum = 0;
while (n > 0) {
int d = n % 10;
n = n / 10;
totalSum += d * d;
}
return totalSum;
}
}