题目描述
有一位使者要游历各国,他每到一个国家,都能学到一种文化,但他不愿意学习任何一种文化超过一次(即如果他学习了某种文化,则他就不能到达其他有这种文化的国家)。不同的国家可能有相同的文化。不同文化的国家对其他文化的看法不同,有些文化会排斥外来文化(即如果他学习了某种文化,则他不能到达排斥这种文化的其他国家)。
现给定各个国家间的地理关系,各个国家的文化,每种文化对其他文化的看法,以及这位使者游历的起点和终点(在起点和终点也会学习当地的文化),国家间的道路距离,试求从起点到终点最少需走多少路。
输入格式
第一行为五个整数 N,K,M,S,TN,K,M,S,T,每两个整数之间用一个空格隔开,依次代表国家个数(国家编号为11 到 NN),文化种数(文化编号为 11 到 KK),道路的条数,以及起点和终点的编号(保证 SS 不等于 TT);
第二行为 NN个整数,每两个整数之间用一个空格隔开,其中第 ii个数 C_iCi,表示国家 ii的文化为 C_iCi。
接下来的 KK行,每行 KK 个整数,每两个整数之间用一个空格隔开,记第ii 行的第 j 个数为 a_{ij}aij,a_{ij}= 1aij=1 表示文化 ii 排斥外来文化jj(ii 等于 jj 时表示排斥相同文化的外来人),a_{ij}= 0aij=0 表示不排斥(注意 ii 排斥 jj 并不保证 jj 一定也排斥 ii)。
接下来的 MM 行,每行三个整数 u,v,du,v,d,每两个整数之间用一个空格隔开,表示国家 uu与国家 vv有一条距离为dd的可双向通行的道路(保证uu不等于 vv,两个国家之间可能有多条道路)。
输出格式
一个整数,表示使者从起点国家到达终点国家最少需要走的距离数(如果无解则输出-1−1)。
输入数据 1
2 2 1 1 2
1 2
0 1
1 0
1 2 10
Copy
输出数据 1
-1
Copy
输入数据 2
2 2 1 1 2
1 2
0 1
0 0
1 2 10
Copy
输出数据 2
10
Copy
提示
输入输出样例说明11
由于到国家 22 必须要经过国家11,而国家22的文明却排斥国家 11 的文明,所以不可能到达国家 22。
输入输出样例说明22
路线为11 ->22
【数据范围】
对于 100%的数据,有2≤N≤1002≤N≤100
1≤K≤1001≤K≤100
1≤M≤N^21≤M≤N2
1≤k_i≤K1≤ki≤K
1≤u, v≤N1≤u,v≤N
1≤d≤1000,S≠T,1≤S,T≤N1≤d≤1000,S=T,1≤S,T≤N
NOIP 2012 普及组 第四题
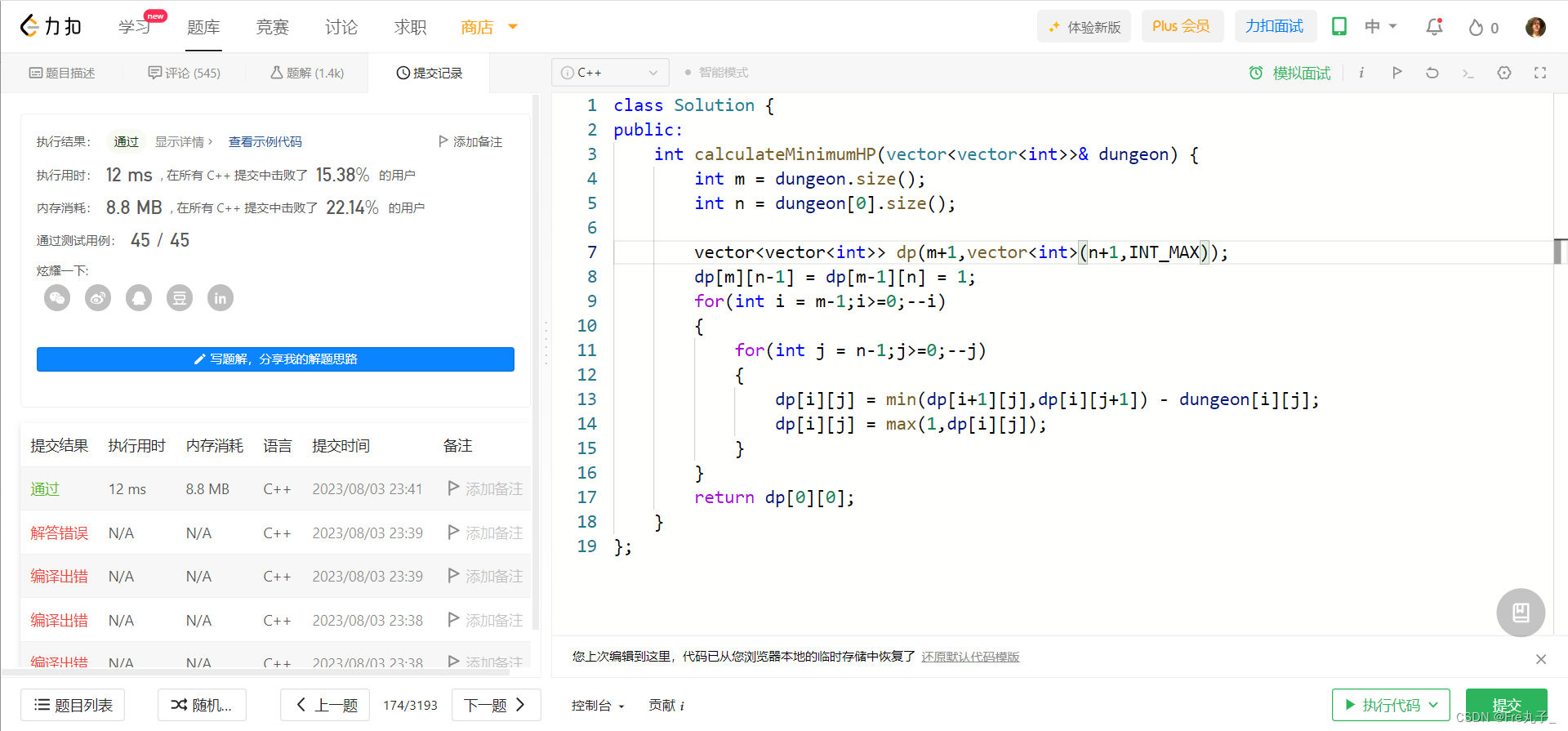
代码:
#include <cstdio>
#include <cstring>
int n,k,m,s,t,country[105],first[20005],next[20005],v[20005],w[20005];
int wh[105][105],cnt,head,tail,q[100005],dis[105];
int q1[100005][105];
using namespace std;
inline int read()
{
int f=1,x=0;
char ch=getchar();
if (ch=='-')
{
f=-1;
ch=getchar();
}
while ((ch<'0')||(ch>'9')) ch=getchar();
while ((ch>='0')&&(ch<='9'))
{
x=x*10+ch-48;
ch=getchar();
}
return f*x;
}
inline void spfa(int s)
{
memset(dis,0x3f3f3f3f,sizeof(dis));//dis数组记录的是s点到所有点的距离
dis[s]=0;
head=0;
tail=1;
q[1]=s;
q1[1][0]=1;//q1[i][0]记录的是知道了多少种文化
q1[1][1]=country[s];
while (head<tail)
{
head=head%100000+1;
for (int i=first[q[head]];i;i=next[i])
{
int k=v[i];//k为目标点
bool bo=0;
for (int j=1;j<=q1[head][0];j++)//判断目标点可否到达
if (wh[country[k]][q1[head][j]]||(country[k]==q1[head][j]))
{
bo=1;
break;
}
if (bo) continue;//不可到达,则跳过
if (dis[q[head]]+w[i]<dis[k])//如果可以使距离变短的话,就加入
{
dis[k]=dis[q[head]]+w[i];
tail=tail%100000+1;
q[tail]=k;
q1[tail][0]=q1[head][0]+1;
for (int j=1;j<=q1[head][0];j++)
q1[tail][j]=q1[head][j];
q1[tail][q1[tail][0]]=country[k];
}
}
}//下面判断输出
if (dis[t]==0x3f3f3f3f)
{
printf("-1\n");
return;
} else
{
printf("%d\n",dis[t]);
return;
}
}
int main()
{
n=read(),k=read(),m=read(),s=read(),t=read();
for (int i=1;i<=n;i++) country[i]=read();
for (int i=1;i<=k;i++)
for (int j=1;j<=k;j++) wh[i][j]=read();
for (int i=1;i<=m;i++)
{
int x,y,z;
x=read(),y=read(),z=read();
next[++cnt]=first[x];
first[x]=cnt;
v[cnt]=y;
w[cnt]=z;
next[++cnt]=first[y];
first[y]=cnt;
v[cnt]=x;
w[cnt]=z;
}
spfa(s);
return 0;
}