著名的残差网络主要是在两片论文里提出：

1. Deep Residual Learning for Image Recognition
2. Identity Mappings in Deep Residual Networks

其中第一篇主要讲的是残差网络模块，简单介绍了下基本逻辑。然后就是引入到VGG-19网络中去，来验证残差网络的先进性。
第二篇就是深入讨论了这个残差背后的逻辑，并进一步优化了这个残差结构。

残差网络

深度网络退化

论文提到，基本上深度学习的基本认识是：网络层数越多，拟合能力越强，特征表达能力越强，性能也就越好。
随着网络的加深，例如计算资源的瓶颈，过拟合问题，梯度消失或者梯度爆炸的问题，基本上都被各种方法解决了。
比如计算资源就可以通过GPU的并行计算大幅度提升；
过拟合问题通过日益增多的标签数据量，还有dropout等方案来解决；
梯度消失或者梯度爆炸的问题，也通过引入Batch Normalization层可以解决。

上述问题解决后，不管是AlexNet，VGG还是GoogleLeNet，都是不断的提升网络深度，并且通过提升网络深度获得了较好的性能。
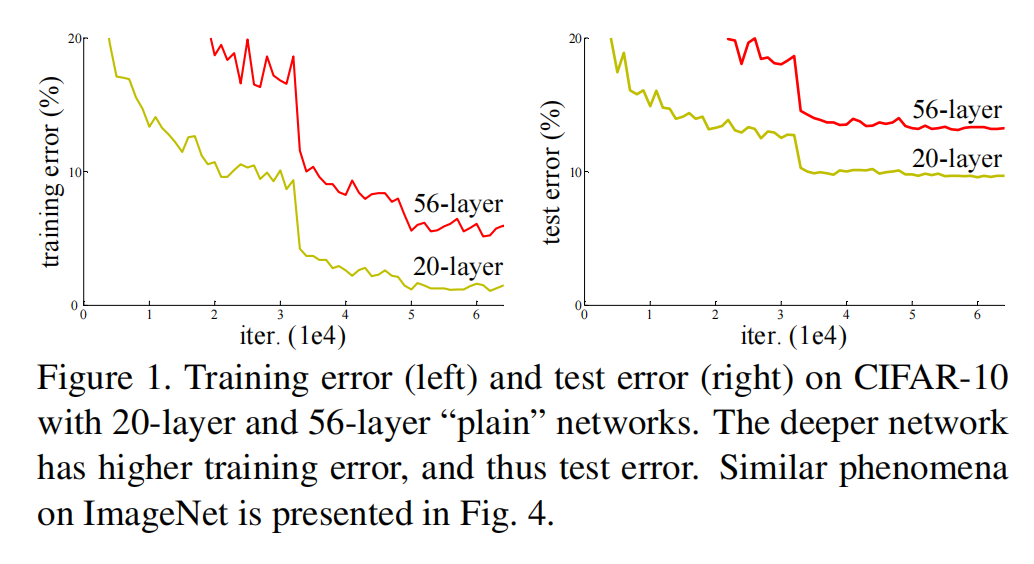
但是，论文里提到，随着网络继续加深，会出现一个叫做网络退化的问题（Degradation Problem），这种退化并不是由过拟合引起的，并且在适当深度的模型中增加更多的层会导致更高的训练误差。如果是overfitting的话，则会出现训练误差小，测试误差大的现象。
原文描述：When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher train- ing error, and thoroughly verified by our experiments。

实验结果：

残差结构

为了解决这个退化问题，论文提出了大名鼎鼎的残差网络residual network，如下图：

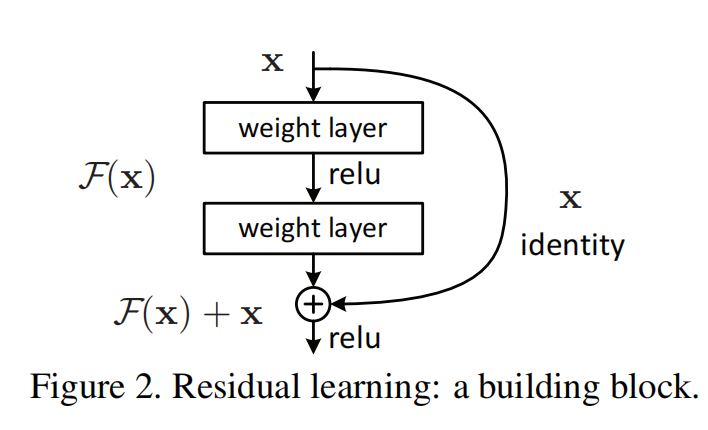
残差结构的基本逻辑是这样的：

1. 在一个卷积层block的旁边增加一条通路(shortcut connections)，从这个block的输入直接连接到卷积的输出。
2. 在这个block的输出处，把卷积层的输出直接加上输入，然后再通过ReLU层。
3. 理论上这个shortcut connections可以跨多层，但是在论文中，作者只使用了两种结构：

• 两个3 * 3的卷积层，下图左边。
• 1个 1 * 1的卷积层用于降维，然后再通过一个3 * 3的卷积层用于提取特征，再通过一个1 * 1的卷积层来恢复维度(通道数)，下图右边。

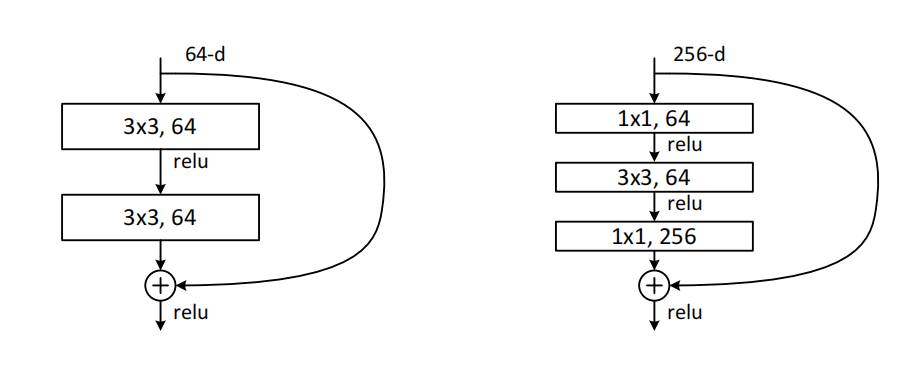
4. 文中提到，这条通路也可以叫做Identity mapping，恒等映射。简单说就是把输入直接复制一下。当然这个也可以采用别的方法，在第二篇论文中就详细的探讨了一下。这个放到下面的章节介绍。

引入了这样一个结构的网络就叫做Residual Network，没有引入的网络叫做Plain Network。

这里写一下我对这个残差结构的理解：在上面的这个残差结构中，定义了几个东西：

• $H(x)$是定义为 underlying mapping to befit by a few stacked layers (not necessarily the entire net)。也就是这个结构需要去拟合或者表达的数据分布，可以被称作为预测值。
• x为输入数据，我理解为真实的数据分布。
• 残差在统计学里被称为预测值与真实值的差异。所以残差就被定义为：$F(x)=H(x)-x$，这部分就是残差。实际上就是卷积层对数据做的映射，$F(x)$也写成$F(x,W_i)$，也就是输入x和权重$W_i$的映射函数。
• 所以在残差网络里，卷积层就是去拟合真实值与预测值之间的差异。
• 而通过shortcut connections可以把真实的数据分布在层与层之间传递(正向或者反向)，保证层与层之间不出现信息差(梯度消失或者梯度爆炸)。

残差结构还有一个问题是，卷积出来之后的特征图尺寸不总是和输入的x相同，如果这样的话，还需要对输入x做一些变换之后才能进行相加( The element-wise addition is performed on two feature maps, channel by channel)。也就是：
$$y=F(x,W_i)+W_{s}x$$
关于这个$W_s$矩阵，论文中是说因为对解决退化问题没有什么帮助，所以仅仅用于匹配维度与尺寸， But we will show by experiments that the identity mapping is sufficient for addressing the degradation problem and is economical, and thus Ws is only used when matching dimensions。
就是做一些降维，升维或者padding的事情，我理解第二种残差结构就是为了干这个用的，匹配结构。

残差网络对比测试

plain net VS residual net

对比测试是在VGG的基础网络上测试的，如下图：

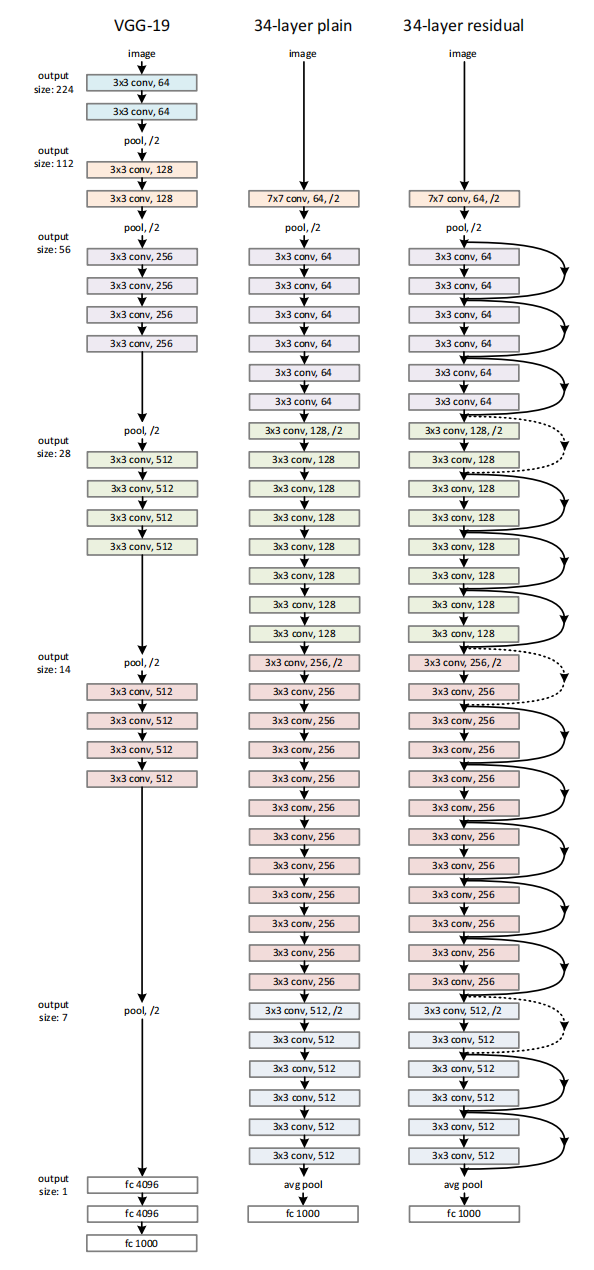
最左边的是VGG-19，中间的是增加到了34层的plain network，最右边的是增加了残差结构，也就是增加了shrotcut connections的网络。
结果分析：

• 18 plain VS 34 plain：

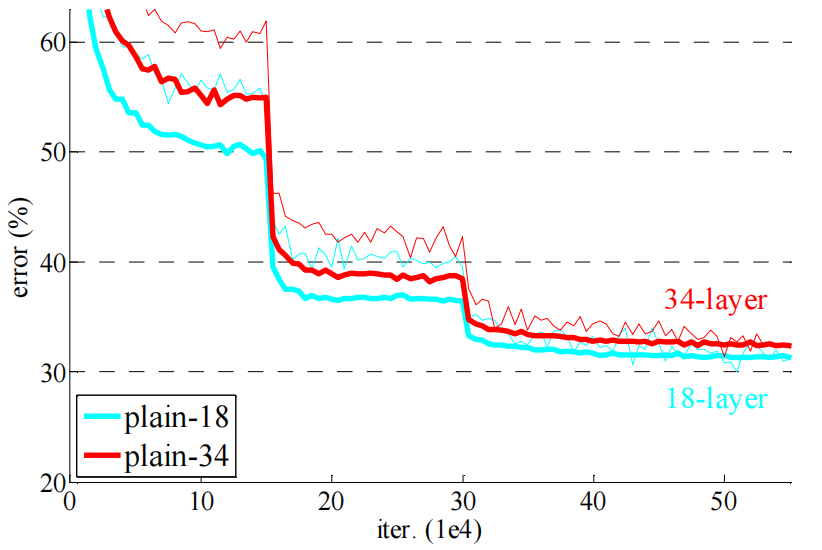
18层的普通网络比34层的表现要好，也就是出现了网络退化现象。

• 然后比较了18层的残差和34层的残差，然后是四个网络(18/34，加不加残差)的结果：

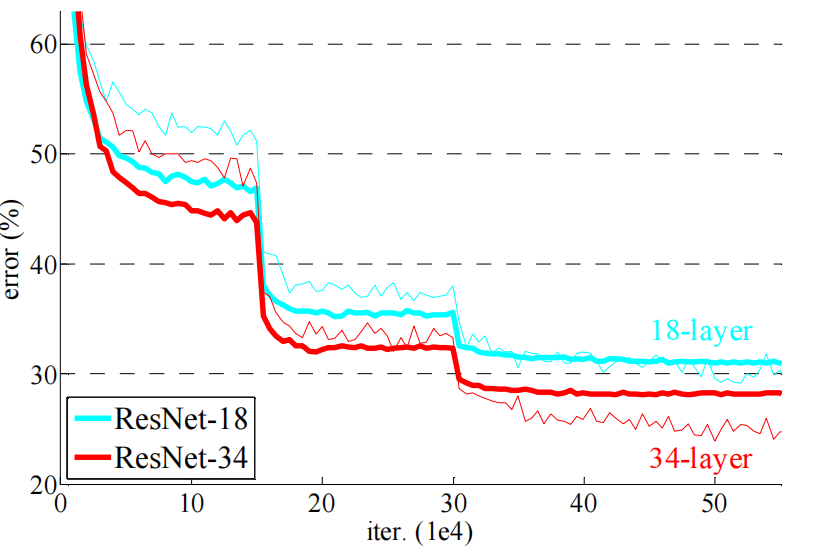
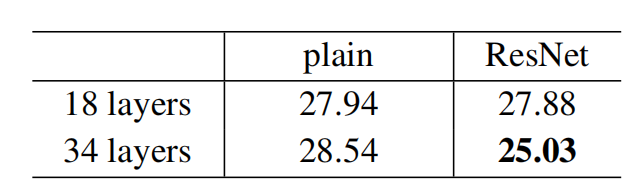
很明显，层数越多，残差的效果越好。

不同的shrotcut connection

前面提到，在那条input-output的connection上，可以用一个矩阵$W_s$去进行dimensions的调整。
文中是基于34层的网络做了三个实验：

• 直接使用zero-padding的方式，直接使用0来做increasing dimensions。最简单的方式，不需要增加任何的参数和计算。
• 使用1 * 1的方式进行补充(只有不匹配的情况下使用)。
• 全部使用1 * 1的方式进行计算(匹配了也再处理一次，不改变尺寸)。

三种情况下的比对结果为：

可以看出A/B/C三种区别不大，为了节省参数，文中是说不再使用第三种方案。

残差网络增加层数

为了验证残差网络在层数不停扩大的情况下的作用，使用了50，101， 152层三种结构，最后一直扩大到了夸张的1202层。在这个层数的实验中，使用的是bottlenect design(在50，101， 152这三个网络中)。就是第二种残差结构，前后各一个1 * 1的卷积层的结构。
结构为：

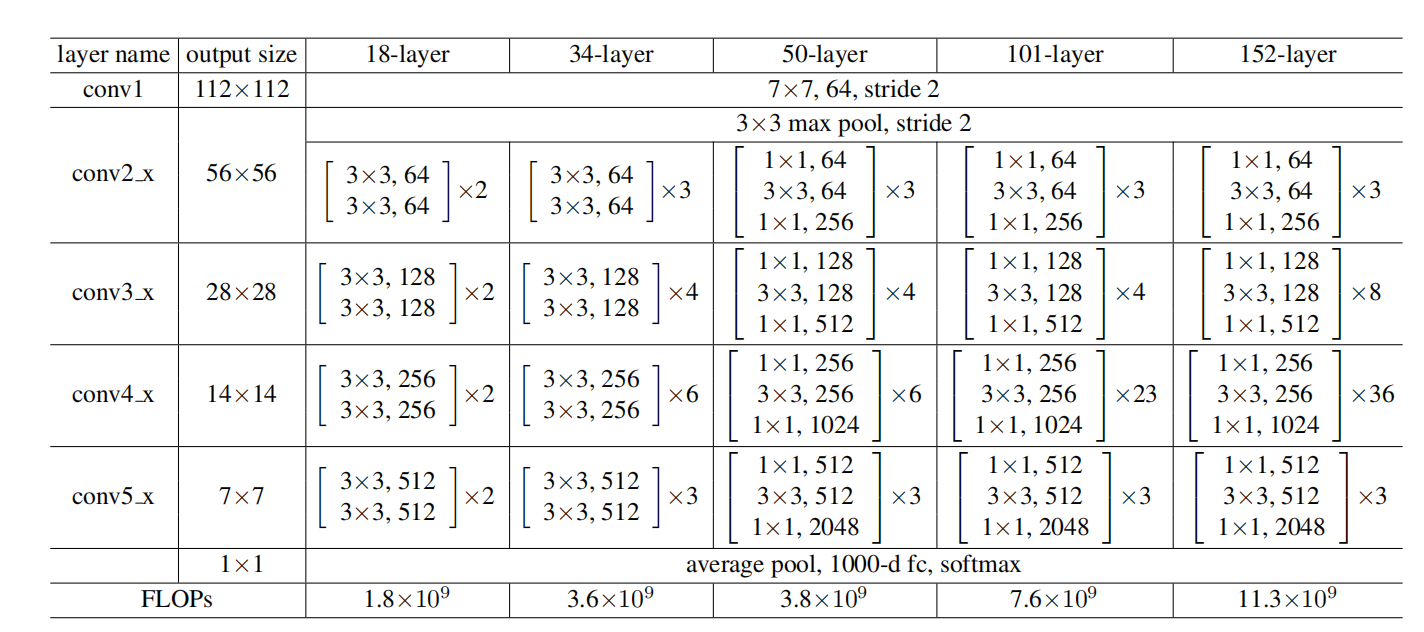
结果为(ImageNet数据集)：

结果证明，残差结构能有效的解决在网络深度增加情况出现的网络退化现象。也就是说，使用残差结构，可以可劲儿的增加层数。效果很好。

最后，论文中弄了一个1202层的非常夸张的网络，这个网络可以将训练精度提升到小于0.1%，但是测试精度就回到了7.93%。还不如浅一点的网络。文中分析的原因可能是因为过拟合，因为数据量太小，数据量不足以支撑这么大的参数量，很容易过拟合。
We argue that this is because of overfitting. The 1202-layer network may be unnecessarily large (19.4M) for this small dataset.