numpy作为数据分析,深度学习常用的库,本篇博客我们来介绍numpy的一些进阶用法:
一,numpy的常用简单内置函数:
1.1求和:
a = np.array([[1, 2],
[3, 4]])
np.sum(a)
101.2求平均值:
np.mean(a) # 求取平均值
2.51.3求最小值:
np.min(a)11.4求最大值:
np.max(a)4以下就不再一一列举,我转成表格大家可以去Python手动尝试一下。
| np.std() | 标准差 |
| np.var() | 方差 |
| np.median() | 中位数 |
| np.power() | 幂运算 |
| np.sart() | 开方 |
| np.log)( | 对数 |
| np.exp() | 指数 |
| np.argsort() | 将元素按照行从小到大排序,返回对应位置元素的下标 |
二,numpy数组运算:
一维数组
2.1加法:
array([ 9, 18, 27, 36, 45])a = np.array([10, 20, 30, 40, 50])
b = np.arange(1, 6)
print(a + b)
array([11, 22, 33, 44, 55])2.2减法
a - b
array([ 9, 18, 27, 36, 45])2.3乘法:
a * b
array([ 10, 40, 90, 160, 250])2.4除法:
a / b
array([10., 10., 10., 10., 10.])二维数组:
2.5加法:
A = np.array([[1, 2],
[3, 4]])
B = np.array([[5, 6],
[7, 8]])
print(A+B)[[6,8],
[10,12]]2.6减法:
A-B
[[-4 -4]
[-4 -4]]2.7乘法:
A*B[[ 5 12]
[21 32]]2.8除法:
A/B[[0.2 0.33333333]
[0.42857143 0.5 ]]
三,矩阵运算:
3.1矩阵乘法
A = np.array([[1, 2],
[3, 4]])
B = np.array([[5, 6],
[7, 8]])
print(np.dot(A,B))[[19 22]
[43 50]]3.2矩阵转置
print(A.T)[[1 3]
[2 4]]3.3求逆矩阵
np.linalg.inv(A)[[-2. 1. ]
[ 1.5 -0.5]]四,numpy广播机制:
术语广播是指 NumPy 在算术运算期间处理不同形状的数组的能力。 对数组的算术运算通常在相应的元素上进行。 如果两个阵列具有完全相同的形状,则这些操作被无缝执行。
a = np.array([1,2,3,4])
b = np.array([10,20,30,40])
c = a * b
print(c)[10 40 90 160]
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
b = np.array([1, 2, 3])
# 可直接简写为a+ b, numpy自动实现广播功能,当参与运算的操作数的维度不一样时
a + b
array([[ 2, 4, 6],
[ 5, 7, 9],
[ 8, 10, 12]])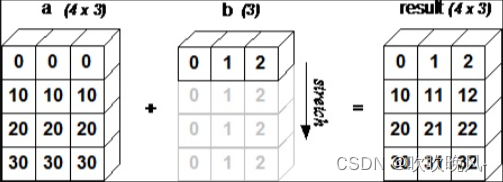
![[模拟电路]集成运算放大器](https://img-blog.csdnimg.cn/28cc38a4d71c44318fe8068c2010fc80.png)