matlab官方帮助文档

https://ww2.mathworks.cn/help/matlab/preprocessing-data.html?s_tid=CRUX_lftnav

平面基本绘图(2D):

• plot的指令格式：plot(x, y, '颜色+曲线格式+曲线符号')
  • x: x轴变量
  • y: y轴变量

颜色:

plot指令  曲线颜色
b         蓝色 (Blue)
c         青蓝色 (Cyan)
g         绿色 (Green)
k         黑色 (Black)
m         紫红色 (Magenta)
r         红色 (Red)
w         白色 (White)
y         黄色 (Yellow)

曲线格式:

plot指令  曲线格式
-         实线 (默认值)
--        虚线
:         点线
-.        点虚线

曲线符号:

plot指令    曲线符号
○          圆形
+          加号
x          叉号
*          星号
.          点号
^          朝上三角形
v          朝下三角形
>          朝右三角形
<          朝左三角形
square     方形
diamond    菱形
pentagram  五角星形
hexagram   六角星形
none       无符号 (默认值)

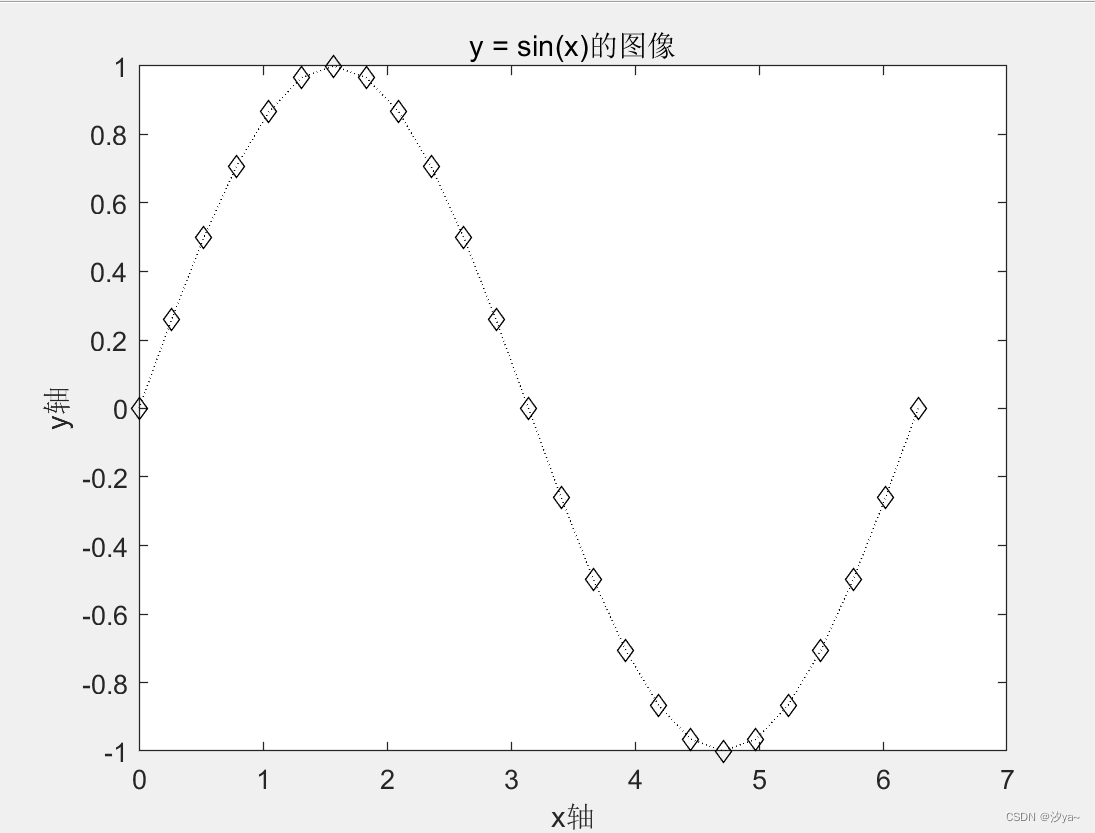
单曲线图

% 生成 x 轴的数据，从 0 到 2*pi，共 25 个点
x = linspace(0, 2*pi, 25);
y = sin(x);

% 绘制图像，'k:diamond' 表示使用黑色线条和菱形符号
plot(x, y, 'k:diamond');

xlabel('x轴');
ylabel('y轴');
title('y = sin(x)的图像');

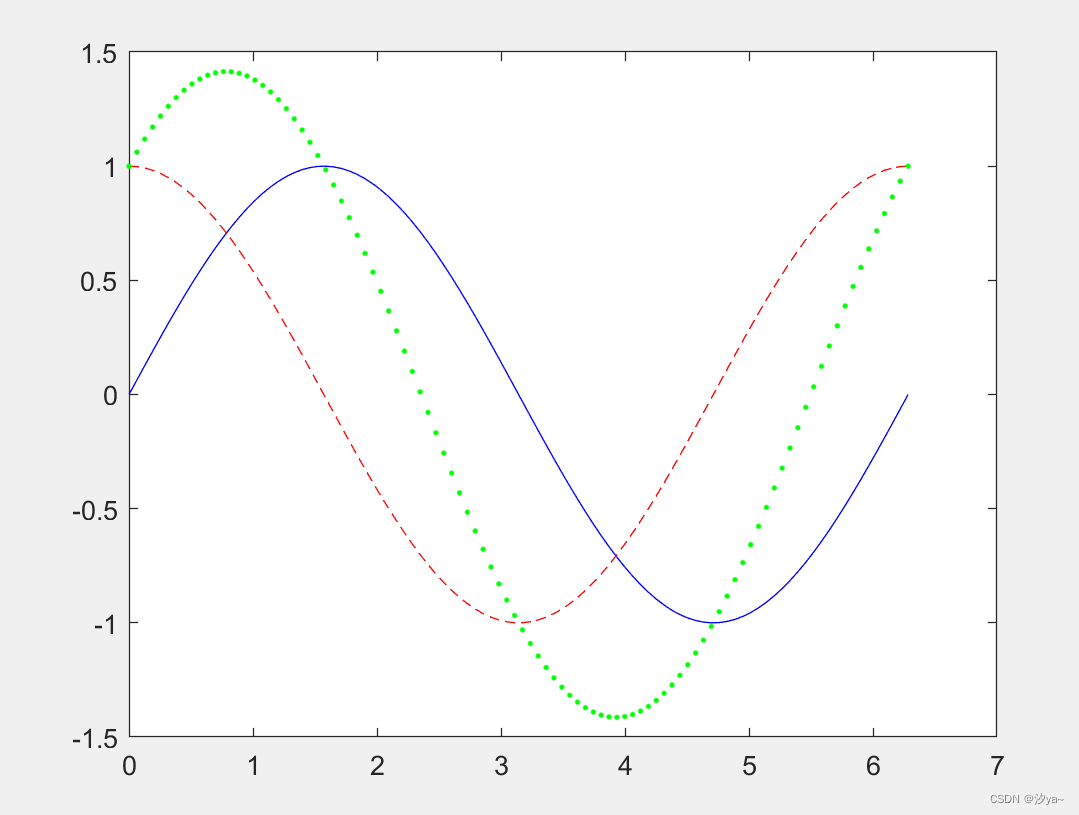
多曲线图

x = linspace(0, 2*pi, 100); % 在 0 到 2*pi 间等分取 100 个点

% 绘制多条曲线并描点作图
plot(x, sin(x), 'b-', x, cos(x), 'r--', x, sin(x) + cos(x), 'g.');

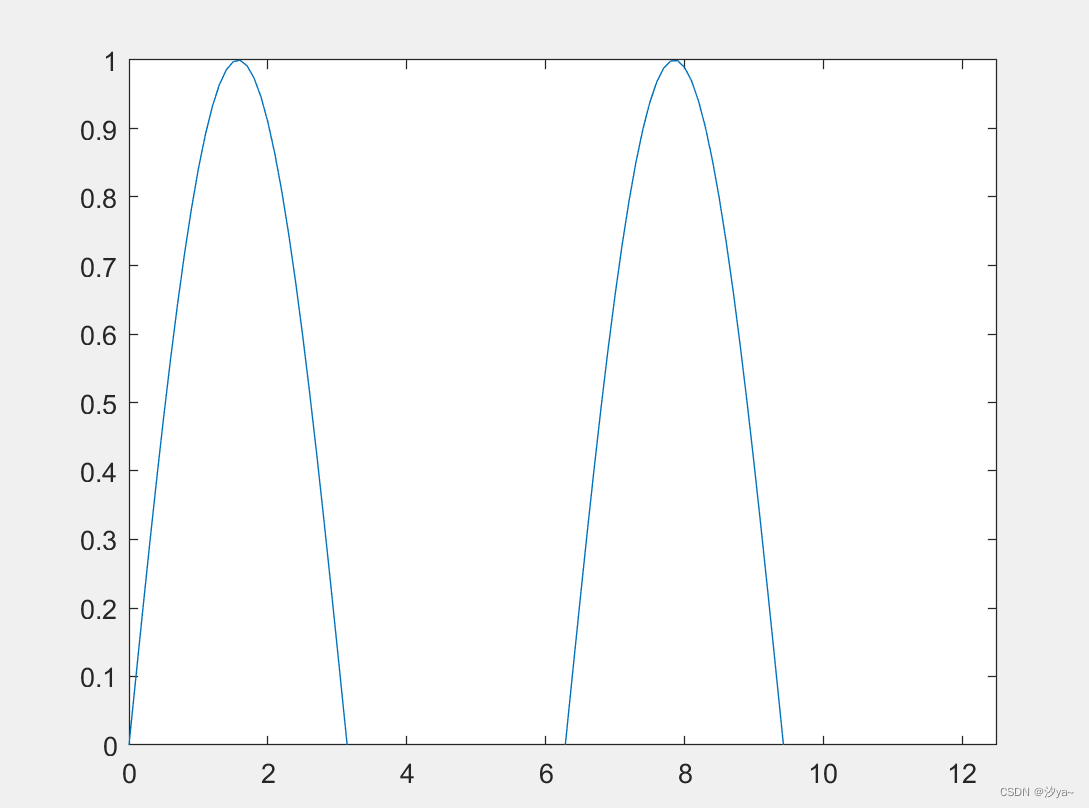
设置画图之 x 轴.y 轴范围 axis([xmin, xmax, ymin, ymax])
xmin: x 轴最小值
xmax： x 轴最大值
ymin: y 轴最小值
ymax： y 轴最大值
注: 设置值若为 -inf 或 inf，指的是数据点的最小值和最大值

x = 0:0.1:4*pi; % x向量的起始与结束元素为0及0.1的各元素相差值
y = sin(x);
plot(x, y);
axis([-inf, inf, 0, 1]); % 画出正弦波y轴介于0和1的部分

以下是转换成Markdown代码格式的内容，使用简体汉字：

改变图轴长宽比：

指令	说明
axis normal	使用默认长宽比（等于图形长宽比）
axis square	长宽比例为1
axis equal	长宽比例不变, 但两轴刻度一致
axis equal tight	两轴刻度比例一致, 且图轴贴紧图形
axis image	两轴刻度比例一致 (适用于影像显示)

改变图轴背景颜色：

指令	说明
colordef white	图轴背景为白色, 视觉背最为浅灰色
colordef black	图轴背景为黑色, 视觉背最为深灰色
colordef none	图轴背最为黑色, 视窗背最为黑色

格线与外框：

指令	说明
grid on	画出格线
grid off	取消格线
box on	画出图轴的外围长方形
box off	取消图轴的外围长方形

加入说明文字： XXX('欲加入之文字')

XXX 可为以下之指令：

指令	说明
title	图形的标题
xlabel	x轴的说明
ylabel	y轴的说明
zlabel	z轴的说明 (适用于立体绘图)
legend	罗条曲线的说明
text	在图形中加入文字
gtext	使用鼠标决定文字的位置

注: text 需指定放置的坐标轴，故使用方法为 text(x轴座标, y轴座标, 欲加入之文字')。

% 设置微软雅黑字体为中文显示
set(groot, 'DefaultAxesFontName', 'Microsoft YaHei');

x = 0:0.1:2*pi;
y1 = sin(x);
y2 = exp(-x);
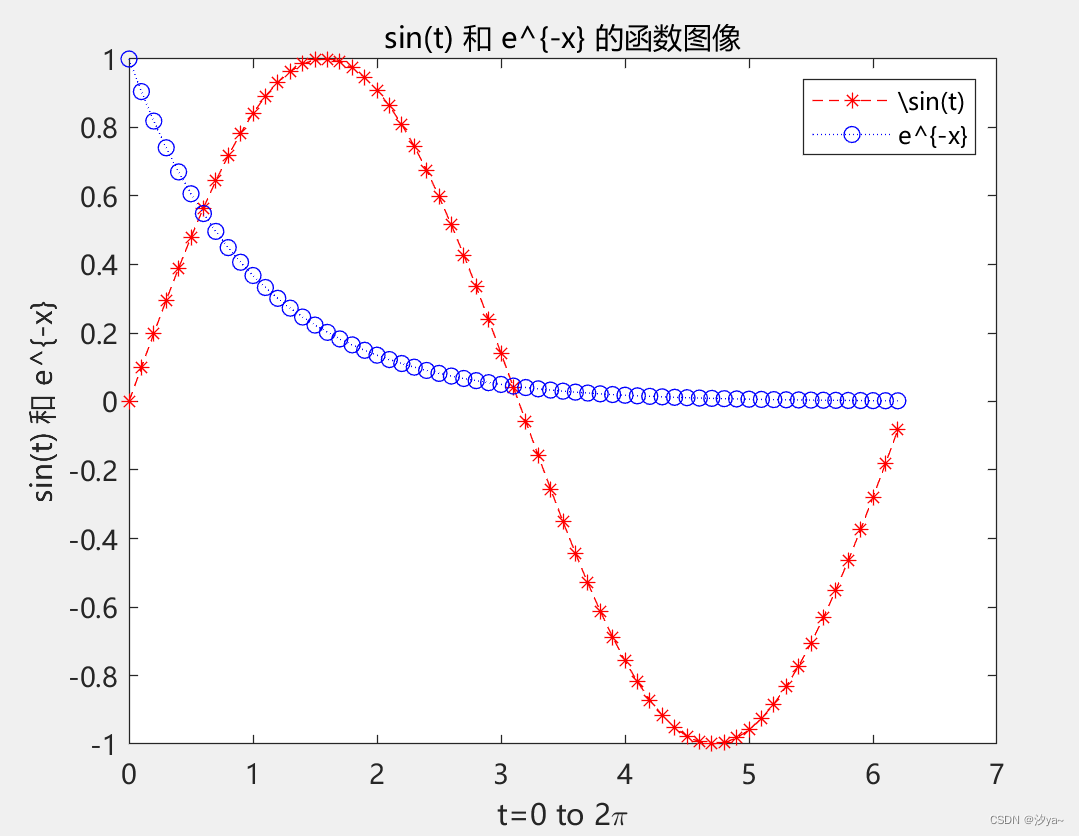
plot(x, y1, '--*r', x, y2, ':ob');
xlabel('t=0 to 2\pi');
ylabel('$\sin(t)$ 和 $e^{-x}$', 'Interpreter', 'latex'); % 使用数学模式的LaTeX表达式显示中文
title('$\sin(t)$ 和 $e^{-x}$ 的函数图像', 'Interpreter', 'latex'); % 使用数学模式的LaTeX表达式显示中文
legend({'$\sin(t)$', '$e^{-x}$'}, 'Interpreter', 'latex'); % 使用数学模式的LaTeX表达式显示中文

% 添加说明文字在图形中的位置
text(1, 0.8, '这是 $\sin(t)$ 的峰值', 'FontName', 'Microsoft YaHei', 'Interpreter', 'latex'); % 添加 x 轴说明文字
text(4, 0.8, '这是 $e^{-x}$ 的衰减', 'FontName', 'Microsoft YaHei', 'Interpreter', 'latex'); % 添加 x 轴说明文字

% 添加箭头指向特定位置
[peak_val_y1, peak_idx_y1] = max(y1);
[decay_val_y2, decay_idx_y2] = max(y2);
annotation('arrow', [peak_idx_y1*0.1/2/pi, peak_idx_y1*0.1/2/pi], [peak_val_y1, 0.6], 'HeadStyle', 'plain'); % 添加指向 sin(t) 峰值的箭头
annotation('arrow', [decay_idx_y2*0.1/2/pi, decay_idx_y2*0.1/2/pi], [decay_val_y2, 0.6], 'HeadStyle', 'plain'); % 添加指向 e^{-x} 峰值的箭头

官网模板

来源:官方
https://ww2.mathworks.cn/products/matlab/plot-gallery.html#

图：https://blog.csdn.net/weixin_43948357/article/details/89220323

单曲线图

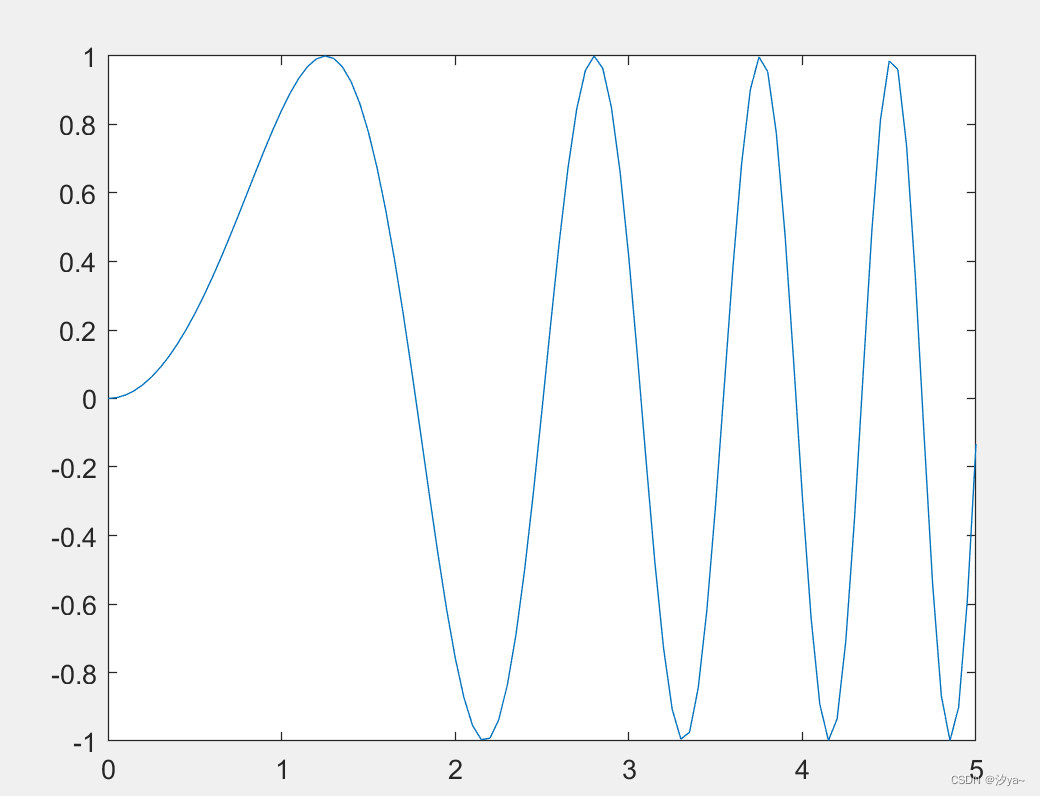
x = 0:0.05:5;
y = sin(x.^2);
figure
plot(x,y)

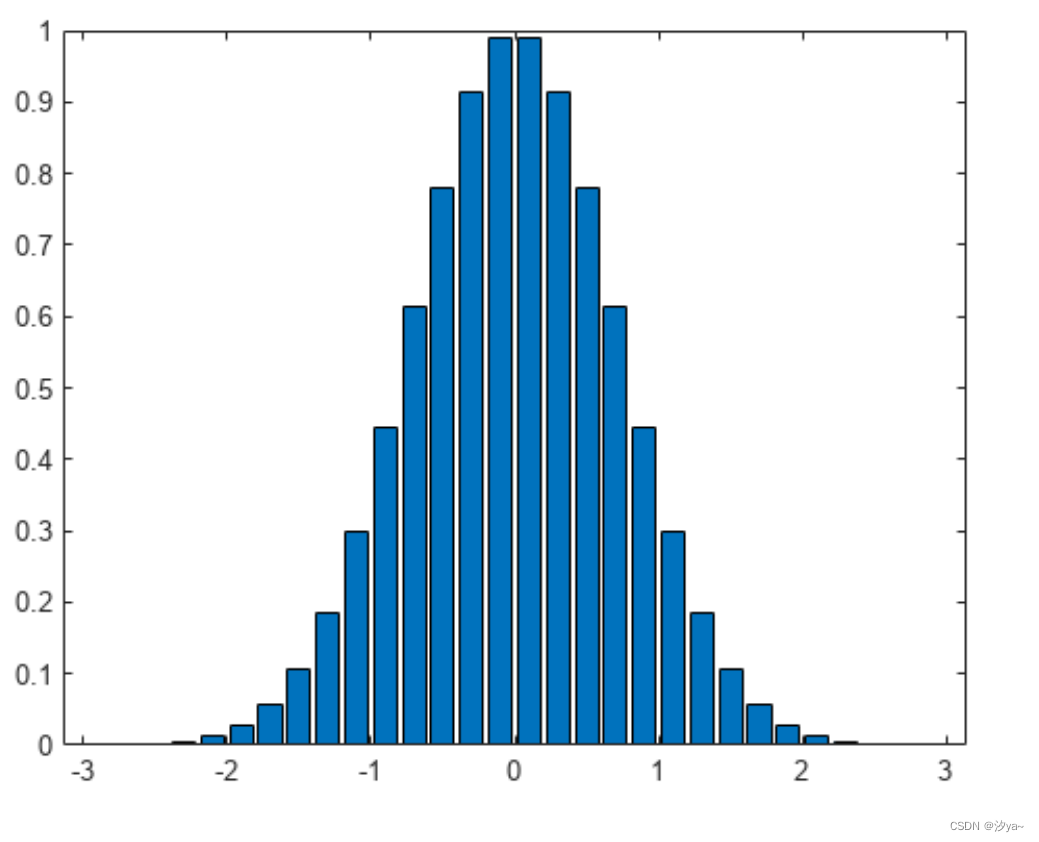
条形图

x = -2.9:0.2:2.9;
y = exp(-x.*x);
bar(x,y)

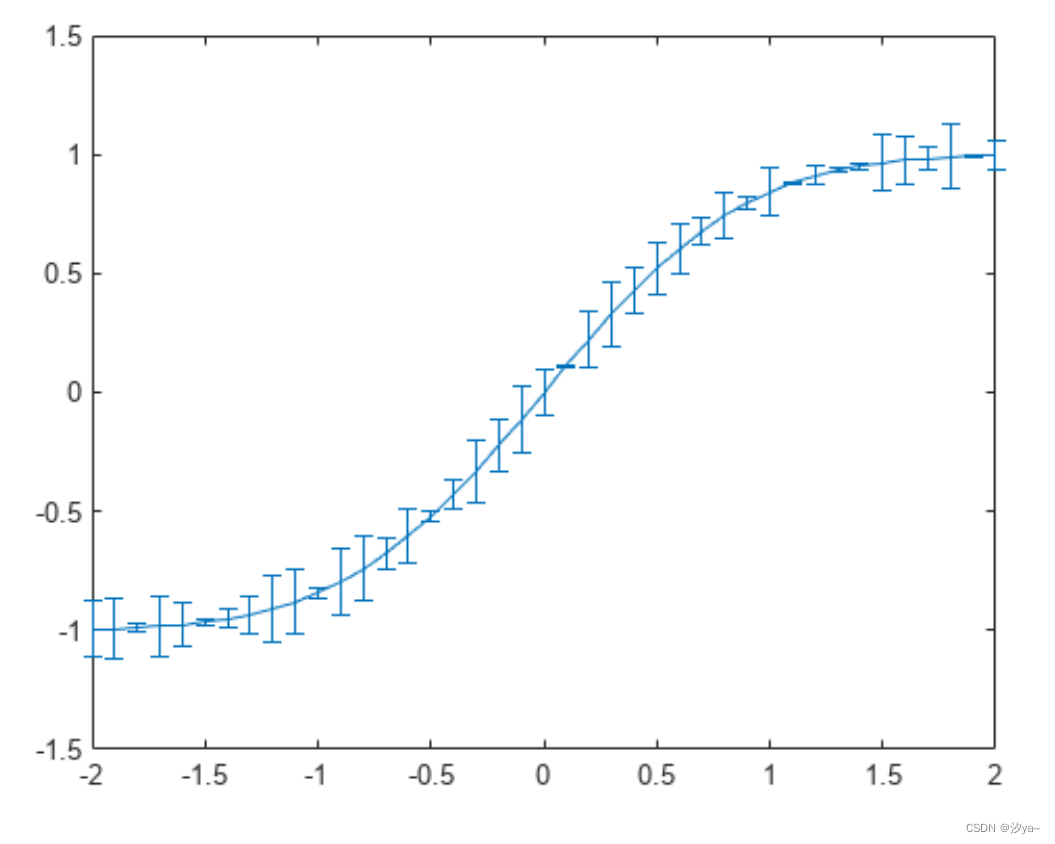
误差条形图

errorbar 函数用来绘制 x 和 y 值的线图并在每个观察点上叠加垂直误差条。若要指定误差条的大小，需要向 errorbar 函数传递一个额外的输入参数。

x = -2:0.1:2;
y = erf(x);
eb = rand(size(x))/7;
errorbar(x,y,eb)

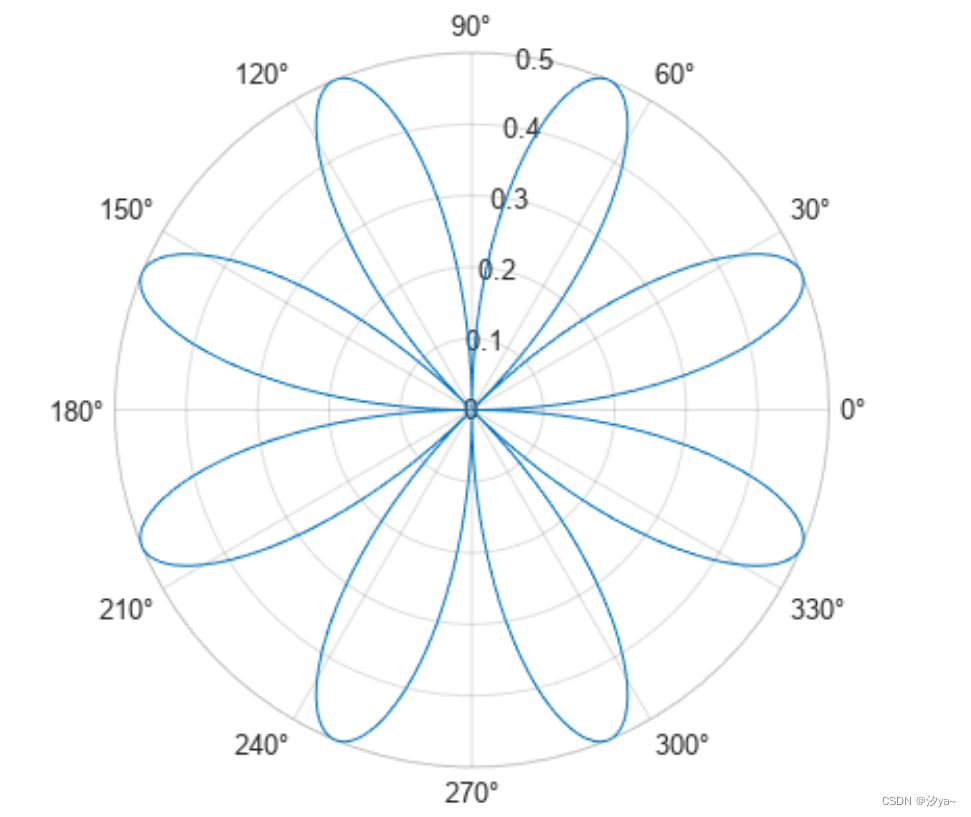
极坐标图

polarplot 函数用来绘制 theta 中的角度值（以弧度为单位）对 rho 中的半径值的极坐标图。

theta = 0:0.01:2*pi;
rho = abs(sin(2*theta).*cos(2*theta));
polarplot(theta,rho)

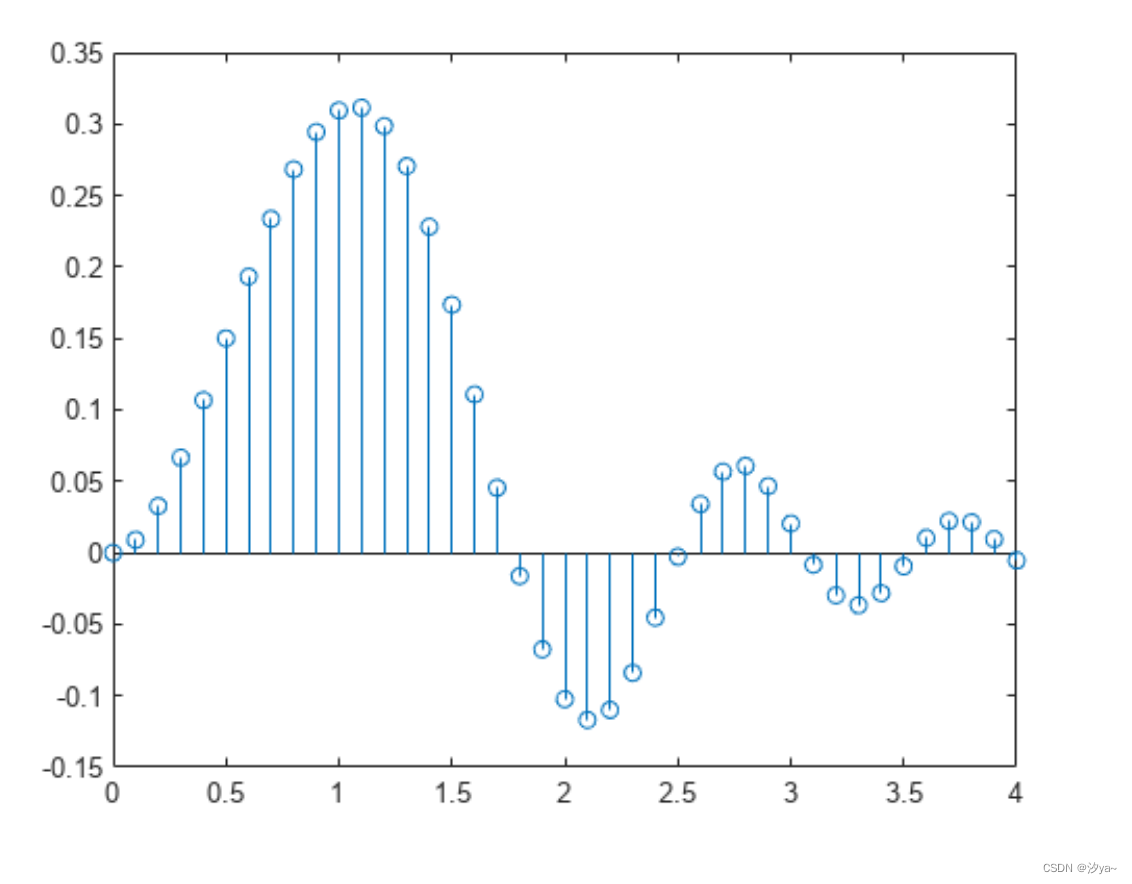
针状图

stem 函数为每个通过竖线连接到一条公共基线的 x 和 y 值绘制一个标记

x = 0:0.1:4;
y = sin(x.^2).*exp(-x);
stem(x,y)

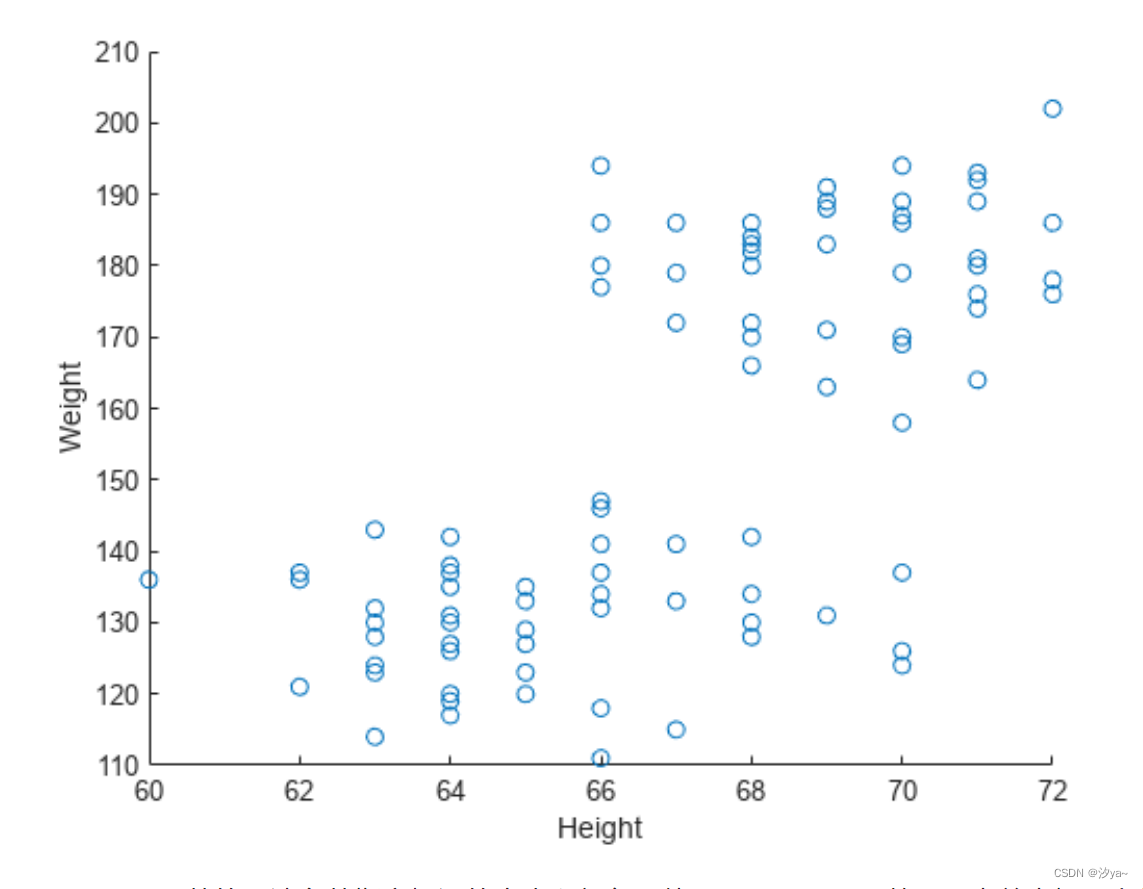
散点图

scatter 函数用来绘制 x 和 y 值的散点图。

load patients Height Weight Systolic
scatter(Height,Weight)
xlabel('Height')
ylabel('Weight')

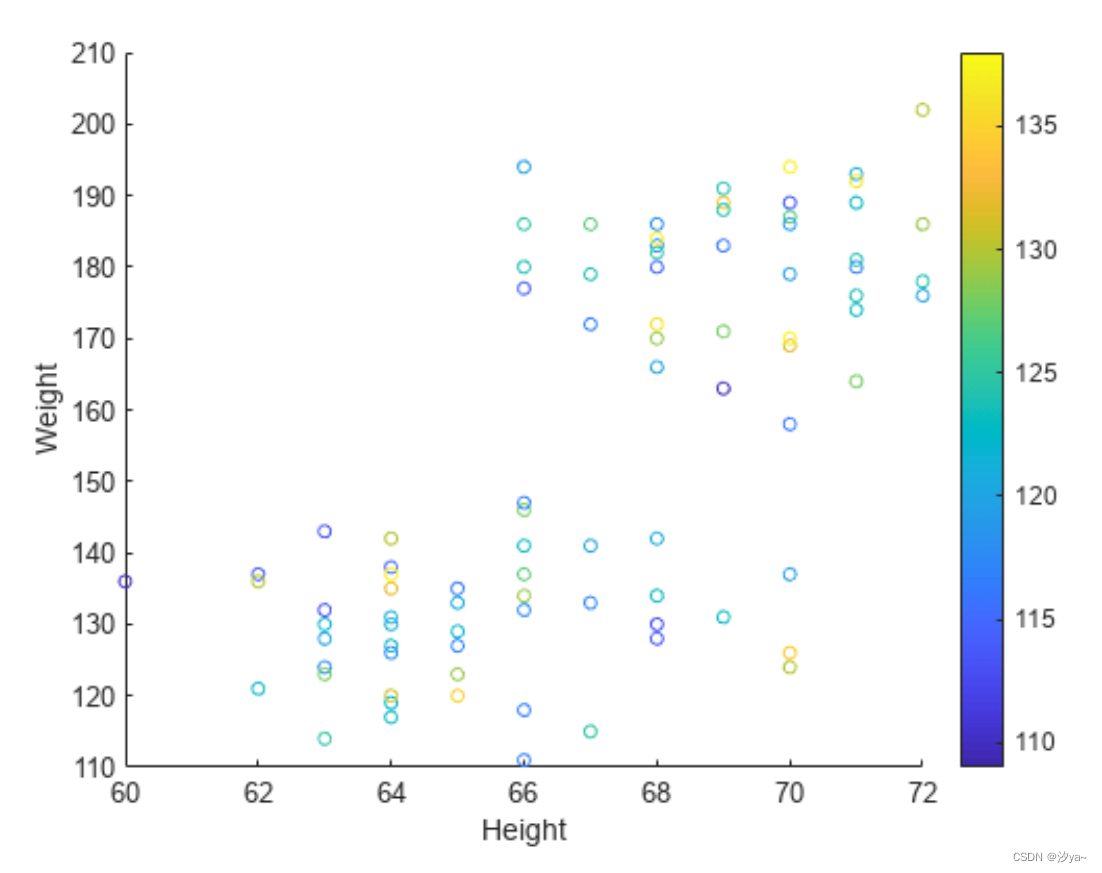
使用 scatter 函数的可选参数指定标记的大小和颜色。使用 colorbar 函数显示当前坐标区上的色阶。

scatter(Height,Weight,20,Systolic)
xlabel('Height')
ylabel('Weight')
colorbar

3D等高线图

3D等高线图包含矩阵Z的等高线，其中Z包含在x-y平面上的高度值。

创建数据：

使用辅助函数meshgrid生成3D等高线图所需的数据，数据之间的关系如下：
[x,y,z] = createData();

基本的3D等高线图：

可视化函数z。等高线颜色根据z方向的高度变化而变化。
contour3(x,y,z);

% 生成数据
[x, y, z] = createData();

% 基本的3D等高线图
% 将矩阵Z中的高度值在x-y平面上表示为等高线
contour3(x, y, z);

% 添加标题和坐标轴标签
title('3D Contour Plot');
xlabel('X Axis');
ylabel('Y Axis');
zlabel('Z Axis');

function [x,y,z] = createData()
    [x,y] = meshgrid(-7:0.1:7);
    z = sin(x) + cos(y);
end

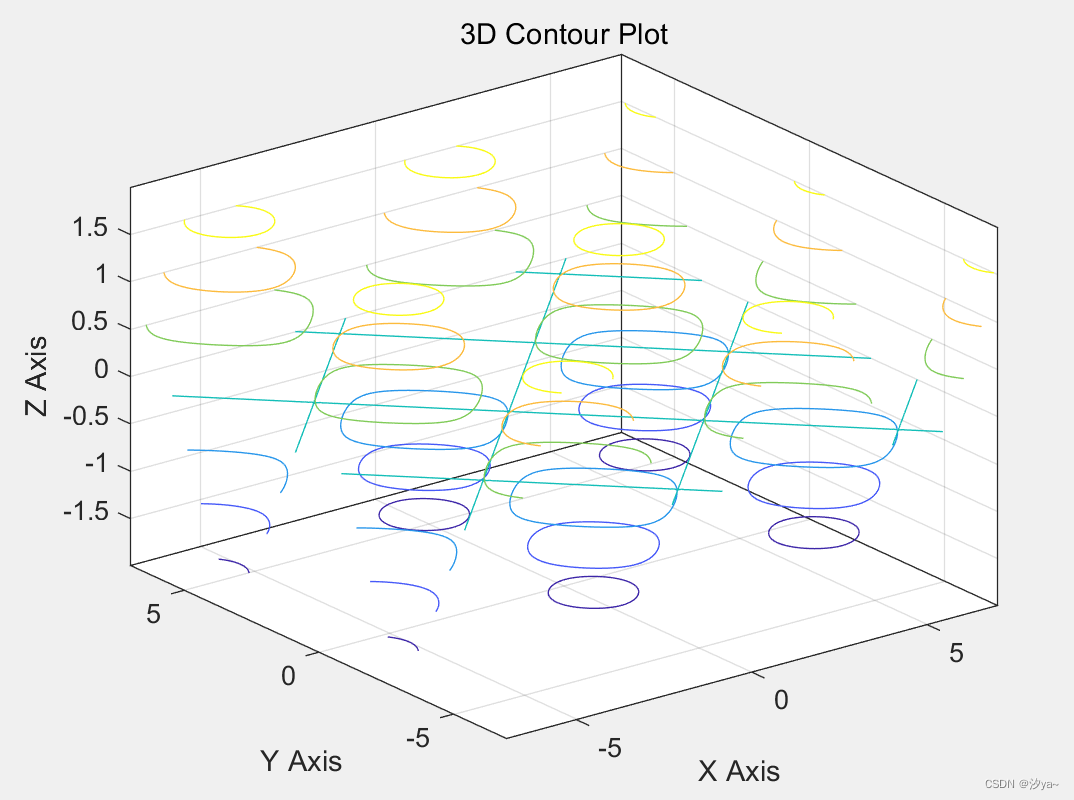
通过将第二个参数传递给contour3函数，您可以指定等高线的数量，从而增加等高线的数量，进而改进可视化效果。同时，您还可以使用“Name-Value”对参数指定等高线的线宽。

% 生成数据
[x, y, z] = createData();

% 基本的3D等高线图
% 将矩阵Z中的高度值在x-y平面上表示为等高线
contour3(x, y, z);

% 添加标题和坐标轴标签
title('3D Contour Plot');
xlabel('X Axis');
ylabel('Y Axis');
zlabel('Z Axis');

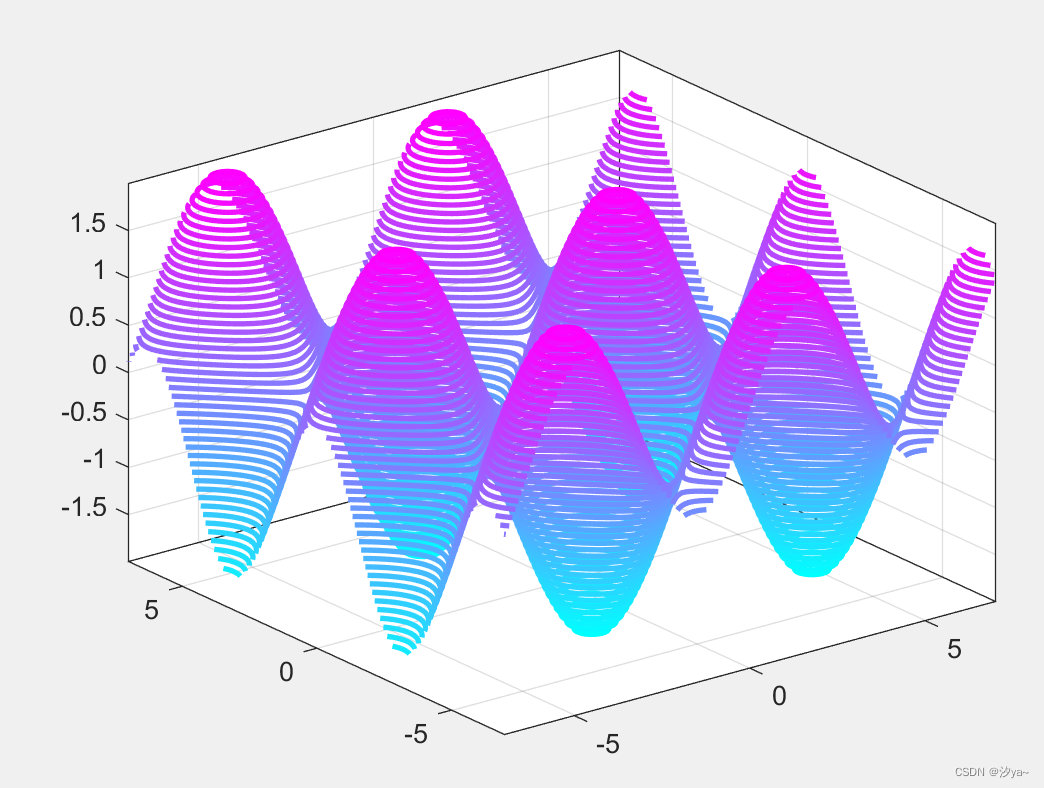
% % 自定义等高线细节
contourLevels = 50;
lineWidth = 2;

figure;
[~,c] = contour3(x, y, z, ...
    contourLevels, ...             % 指定等高线的数量
    'LineWidth', lineWidth);       % 指定等高线的线宽


% 更改颜色映射
colormap("cool");    % 指定等高线图的颜色映射为"cool"

function [x,y,z] = createData()
    [x,y] = meshgrid(-7:0.1:7);
    z = sin(x) + cos(y);
end

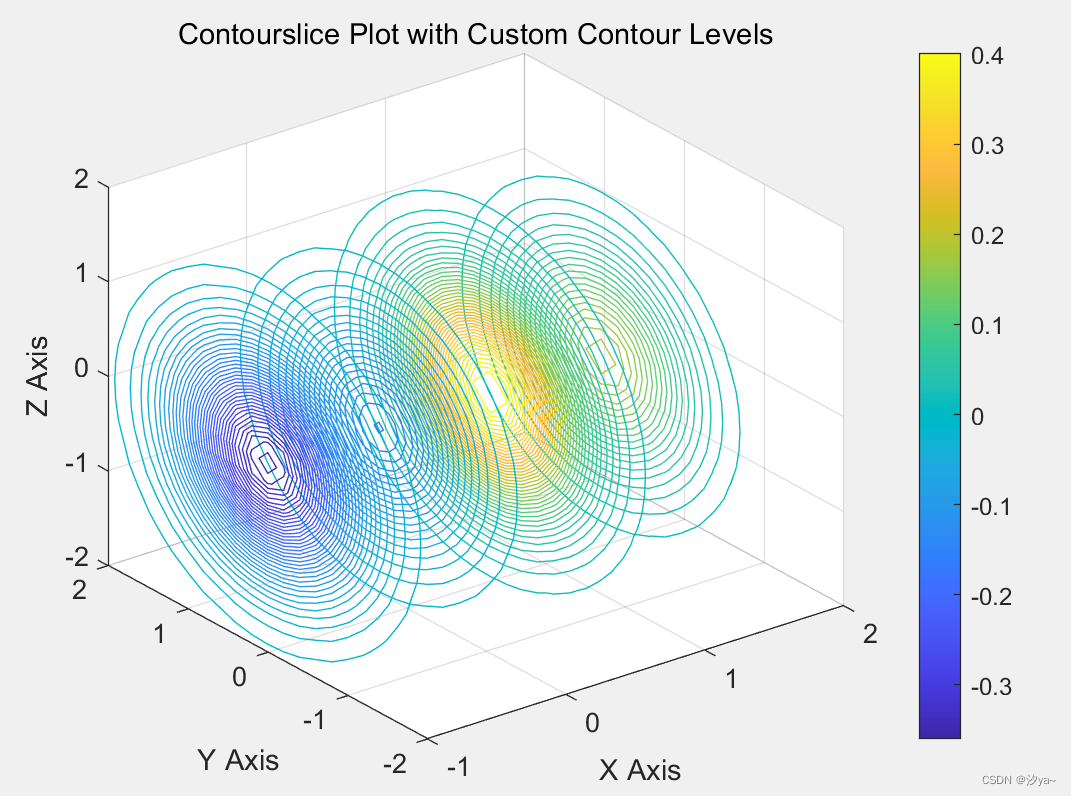
% 生成数据
[X, Y, Z, V] = createData();

% 指定等高线的级别并添加颜色条
figure;
lvls = -0.4:0.01:0.4;
c1 = contourslice(X, Y, Z, V, xslice, [], [], lvls);
view(3);
colorbar;
grid on;
% 添加标题和坐标轴标签
title('Contourslice Plot with Custom Contour Levels');
xlabel('X Axis');
ylabel('Y Axis');
zlabel('Z Axis');

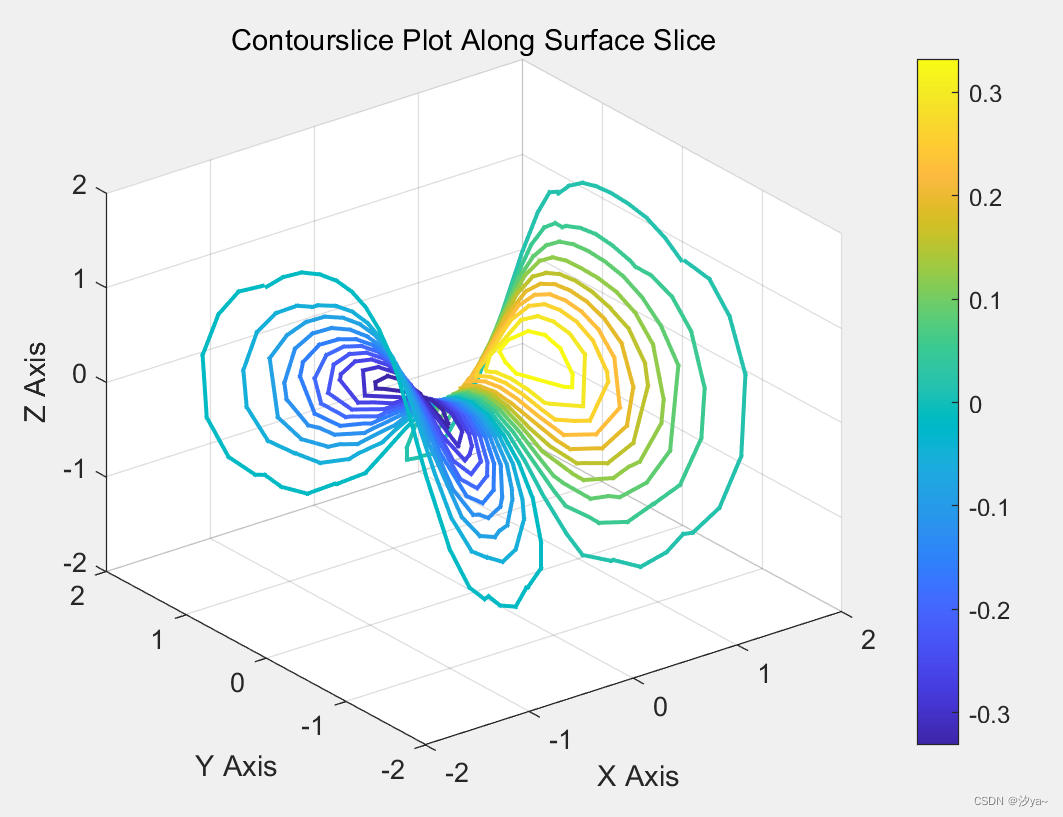
% 沿着曲面切片指定等高线
numContours = 20;
[xsurf, ysurf] = meshgrid(-2:0.2:2);
zsurf = xsurf.^2 - ysurf.^2;

figure;
c2 = contourslice(X, Y, Z, V, xsurf, ysurf, zsurf, numContours);
view(3);
grid on;
colorbar;
% 添加标题和坐标轴标签
title('Contourslice Plot Along Surface Slice');
xlabel('X Axis');
ylabel('Y Axis');
zlabel('Z Axis');

% 更改等高线的线宽
for i = 1:length(c2)
    c2(i).LineWidth = 1.5; % 使用点号表示法更改每个Patch对象的线宽
end

% 辅助函数用于生成数据
function [X, Y, Z, V] = createData()
    [X, Y, Z] = meshgrid(-2:.2:2);
    V = X .* exp(-X.^2 - Y.^2 - Z.^2);
end

热图

进阶版绘图

好看的折线图

% 第一个子图：A4纸的双栏小图，大小为8cmx5cm
figure(1)
set(gcf,'unit','centimeters','position',[10,10,8,5]) % 设置图形窗口位置和尺寸[左 下 宽 高]

linewidth_line = 1.2;     % 图形线条宽度
markersize = 2.5;         % 图形标记点大小
linewidth_gca = 0.7;      % 横纵坐标轴宽度
fontsize_gca = 7;         % 横纵坐标轴刻度字体大小
fontsize_label = 9;       % 横纵坐标轴字体大小
fontsize_legend = 7;      % 图例字体大小

plot(X1,Y1,'--','linewidth',linewidth_line,'markersize',markersize) % 绘制第一条线
hold on;  % 为了能够将多条线画在同一张画布上，需要使用hold on命令
grid on;  % 添加网格线
plot(X2,Y2,'-d','linewidth',linewidth_line,'markersize',markersize) % 绘制第二条线
xlim([0 10])        % X轴坐标范围
ylim([-2.5 2.5])    % Y轴坐标范围
h = legend('图例1','图例2'); % 图例
set(h,'fontsize',fontsize_legend); % 设置图例字体大小
set(gca,'linewidth',linewidth_gca,'fontsize',fontsize_gca) % 设置横纵坐标轴线宽和刻度字体大小
set(gca,'GridLineStyle','--'); % 设置网格线样式为虚线
xlabel('横轴变量名','fontsize',fontsize_label) % 设置横坐标标签字体大小
ylabel('纵轴变量名','fontsize',fontsize_label) % 设置纵坐标标签字体大小
title('A4双栏小图') % 添加标题

% 第二个子图：A4纸的单栏大图，大小为12cmx7.5cm
figure(2)
set(gcf,'unit','centimeters','position',[10,10,12,7.5]) % 设置图形窗口位置和尺寸[左 下 宽 高]

linewidth_line = 1.5;     % 图形线条宽度
markersize = 4;           % 图形标记点大小
linewidth_gca = 0.7;      % 横纵坐标轴宽度
fontsize_gca = 10;        % 横纵坐标轴刻度字体大小
fontsize_label = 12;      % 横纵坐标轴字体大小
fontsize_legend = 9;      % 图例字体大小

plot(X1,Y1,'--','linewidth',linewidth_line,'markersize',markersize)
hold on; grid on;
plot(X2,Y2,'-d','linewidth',linewidth_line,'markersize',markersize)
xlim([0 10])        % X轴坐标范围
ylim([-2.5 2.5])    % Y轴坐标范围
h = legend('图例1','图例2'); % 图例
set(h,'fontsize',fontsize_legend); % 设置图例字体大小
set(gca,'linewidth',linewidth_gca,'fontsize',fontsize_gca) % 设置横纵坐标轴线宽和刻度字体大小
set(gca,'GridLineStyle','--'); % 设置网格线样式为虚线
xlabel('横轴变量名','fontsize',fontsize_label) % 设置横坐标标签字体大小
ylabel('纵轴变量名','fontsize',fontsize_label) % 设置纵坐标标签字体大小
title('A4单栏大图12，7.5') % 添加标题

% 设置输出保存图片的大小和格式
hfig = figure(2);
figWidth = 12;  % 设置图片宽度
figHeight = 7.5;  % 设置图片高度
set(hfig,'PaperUnits','centimeters'); % 图片尺寸所用单位
set(hfig,'PaperPosition',[0 0 figWidth figHeight]);
fileout = 'test2.'; % 输出图片的文件名
print(hfig,[fileout,'tif'],'-r300','-dtiff'); % 设置图片格式、分辨率

% 第三个子图：A4纸的单栏大图，大小为16cmx10cm
figure(3)
set(gcf,'unit','centimeters','position',[10,10,16,10]) % 设置图形窗口位置和尺寸[左 下 宽 高]

linewidth_line = 1.8;     % 图形线条宽度
markersize = 5;           % 图形标记点大小
linewidth_gca = 0.8;      % 横纵坐标轴宽度
fontsize_gca = 12;        % 横纵坐标轴刻度字体大小
fontsize_label = 14;      % 横纵坐标轴字体大小
fontsize_legend = 10;     % 图例字体大小

plot(X1,Y1,'--','linewidth',linewidth_line,'markersize',markersize)
hold on; grid on;
plot(X2,Y2,'-d','linewidth',linewidth_line,'markersize',markersize)
xlim([0 10])        % X轴坐标范围
ylim([-2.5 2.5])    % Y轴坐标范围
h = legend('图例1','图例2'); % 图例
set(h,'fontsize',fontsize_legend); % 设置图例字体大小
set(gca,'linewidth',linewidth_gca,'fontsize',fontsize_gca) % 设置横纵坐标轴线宽和刻度字体大小
set(gca,'GridLineStyle','--'); % 设置网格线样式为虚线
xlabel('横轴变量名','fontsize',fontsize_label) % 设置横坐标标签字体大小
ylabel('纵轴变量名','fontsize',fontsize_label) % 设置纵坐标标签字体大小
title('A4单栏大图16，10') % 添加标题

% 设置输出保存图片的大小和格式
hfig = figure(3);
figWidth = 16;  % 设置图片宽度
figHeight = 10;  % 设置图片高度
set(hfig,'PaperUnits','centimeters'); % 图片尺寸所用单位
set(hfig,'PaperPosition',[0 0 figWidth figHeight]);
fileout = 'test3.'; % 输出图片的文件名
print(hfig,[fileout,'tif'],'-r300','-dtiff'); % 设置图片格式、分辨率

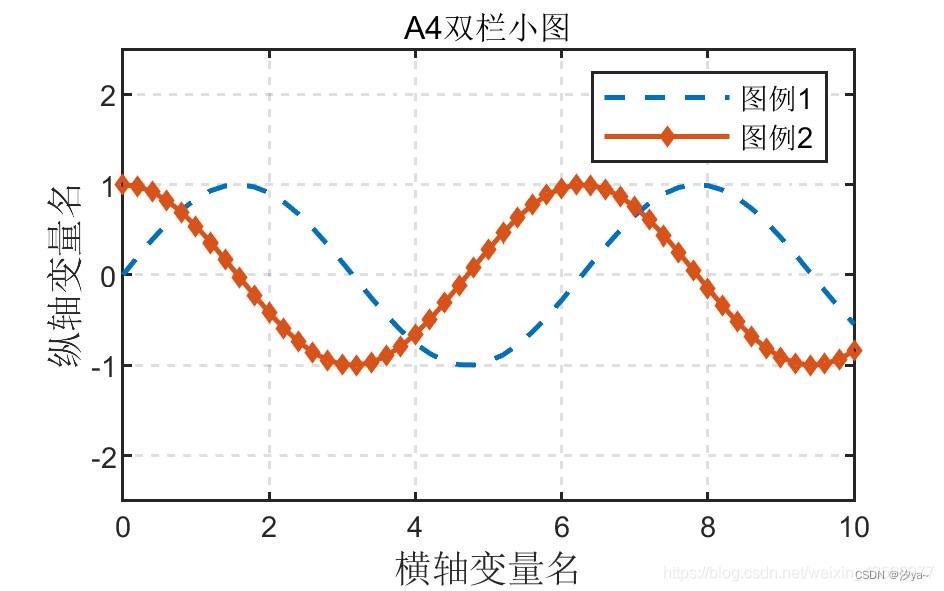
来源https://blog.csdn.net/weixin_43595277/article/details/116332147

柱状图

% 创建新的画布
figure;

% 第一个子图：展示两组柱状图的比较
y = [300 311; 390 425; 312 321; 250 185; 550 535; 420 432; 410 520;];
subplot(1, 3, 1);
b = bar(y);
grid on;
set(gca, 'XTickLabel', {'0', '1', '2', '3', '4', '5', '6'})
legend('算法1', '算法2');
xlabel('x 轴');
ylabel('y 轴');

% 第二个子图：使仅有的一组柱状图呈现不同颜色，默认的是相同颜色
data = [1.0, 1.0, 0.565, 0.508, 0.481, 0.745];
subplot(1, 3, 2);
b = bar(data);
ch = get(b, 'children');
set(ch, 'FaceVertexCData', [4; 2; 3; 1; 5; 6]); % 使用Indexed形式指定每组bar的颜色
set(gca, 'XTickLabel', {'C0', 'C1', 'C2', 'C3', 'C4', 'C5'})
axis([0 7 0.0 1.0]);
ylabel('micro F-measure');

% 第三个子图：使每个bar颜色不同，默认的是每个元素在不同组的颜色相同
data = [3, 7, 5, 2; 4, 3, 2, 9; 6, 6, 1, 4];
subplot(1, 3, 3);
b = bar(data);
ch = get(b, 'children');
set(ch{1}, 'FaceVertexCData', [1; 2; 3]); % 设置第一个元素在不同组的颜色
set(ch{2}, 'FaceVertexCData', [1; 2; 3]); % 设置第二个元素在不同组的颜色
set(ch{3}, 'FaceVertexCData', [1; 2; 3]);
set(ch{4}, 'FaceVertexCData', [1; 2; 3]);

% 添加注释

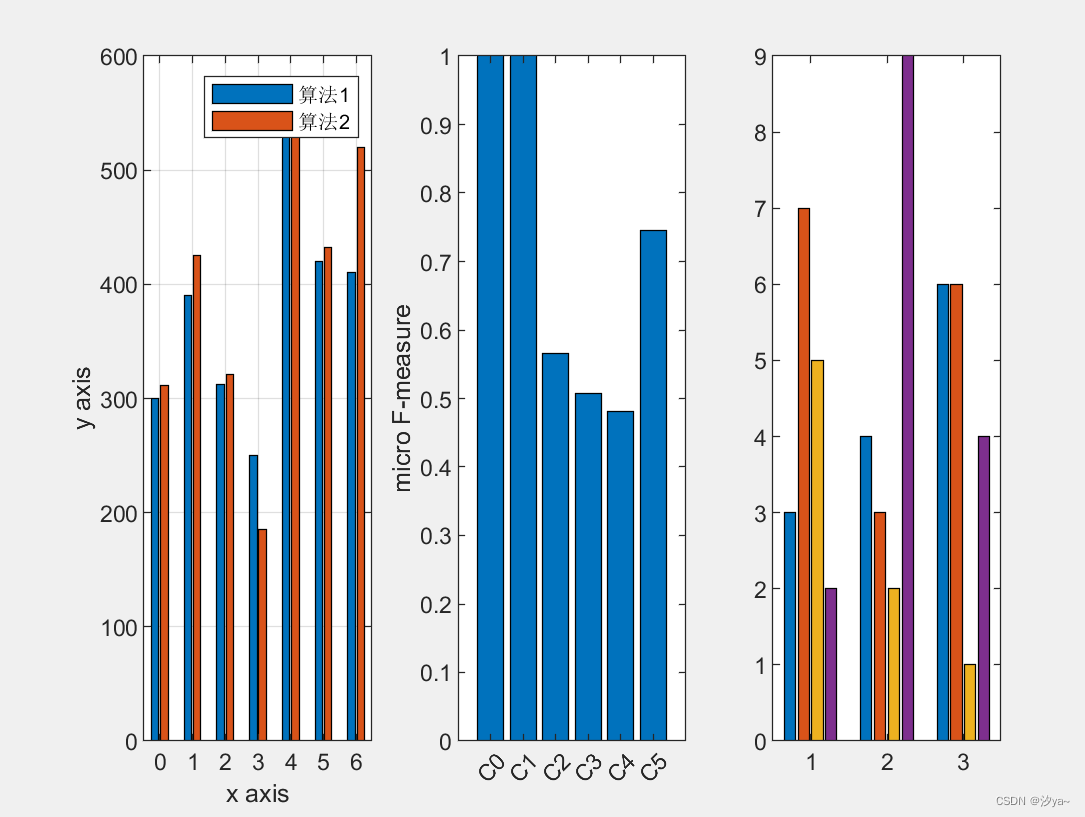
统计直方图

x = -10:.1:10;                  % 创建向量x，范围为-10到10，步长为0.1
y1 = randn(2008, 1);            % 生成2008个符合正态分布的随机数，存储在向量y1中
y2 = randn(2008, 3);            % 生成2008行3列符合正态分布的随机数，存储在矩阵y2中

figure;                         % 创建新的图形窗口

colormap(winter);               % 设置色图为winter颜色映射

% subplot(2,2,1): y1为向量，使用默认的10个条目，显示y1的直方图
subplot(2,2,1);
hist(y1);
title('y1为向量，default, n=10');  % 设置子图标题

% subplot(2,2,2): y2为矩阵，对每列进行处理，显示多组条形
subplot(2,2,2);
hist(y2);
title('y2为矩阵');               % 设置子图标题

% subplot(2,2,3): 向量x指定条目，计算y1中每个bin的频率并绘制条形直方图
subplot(2,2,3);
hist(y1, x);
% 或者使用以下两行代码，获取n和xout的值，然后用bar函数绘制条形直方图
% [n, xout] = hist(y1, x);
% bar(xout, n);
title('向量x指定条目');          % 设置子图标题

% subplot(2,2,4): 使用nbins=1000指定bin的数目，计算y2中每个bin的频率并绘制条形直方图
subplot(2,2,4);
hist(y2, 1000);
title('nbins=1000');            % 设置子图标题

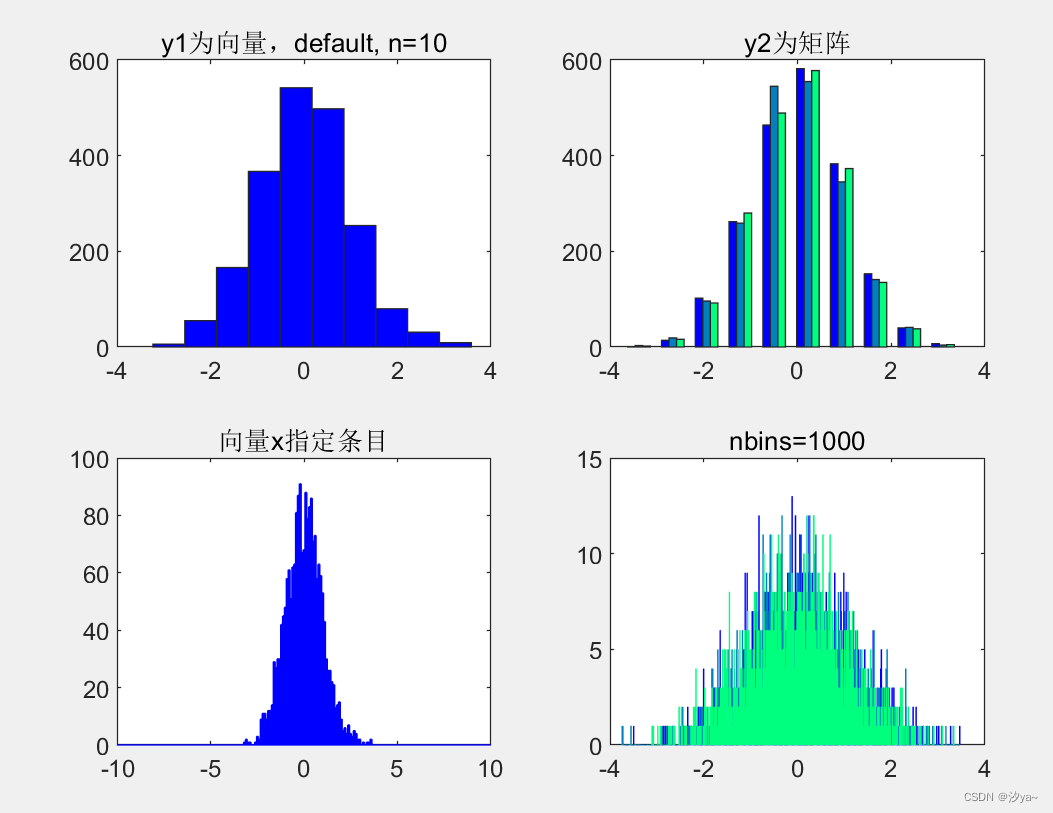
离散数据杆状图

%stem和stem3函数用于绘制二维或三维的离散数据杆状图
%stem(Y)可以理解成绘制离散点的plot(y)函数
%stem(X,Y)可以理解成绘制离散点的plot(x,y)函数
%stem(...,'filled')改变数据点显示的空、实状态。
%stem(...,'LINESPEC')Linespec代表直线属性设置参量。
x=1:.1:10;
y=exp(x.*sin(x));
figure;
subplot(1,3,1);
plot(x,y,'.-r');
title('plot(x,y)');
subplot(1,3,2);
stem(x,y,'b');
subplot(1,3,3);
stem(x,y,':g','fill');
%绘制三维离散杆状图
th=(0:127)/128*2*pi;% 角度采样点
x=cos(th);
y=sin(th);
f=abs(fft(ones(10,1),128)); %对离散方波进行 FFT 变换，并取幅值
stem3(x,y,f','cd','fill');%绘制图形
view([-65 30]);
xlabel('Real'); %图形标注
ylabel('Imaginary');
zlabel('Amplitude');
title('FFT example');

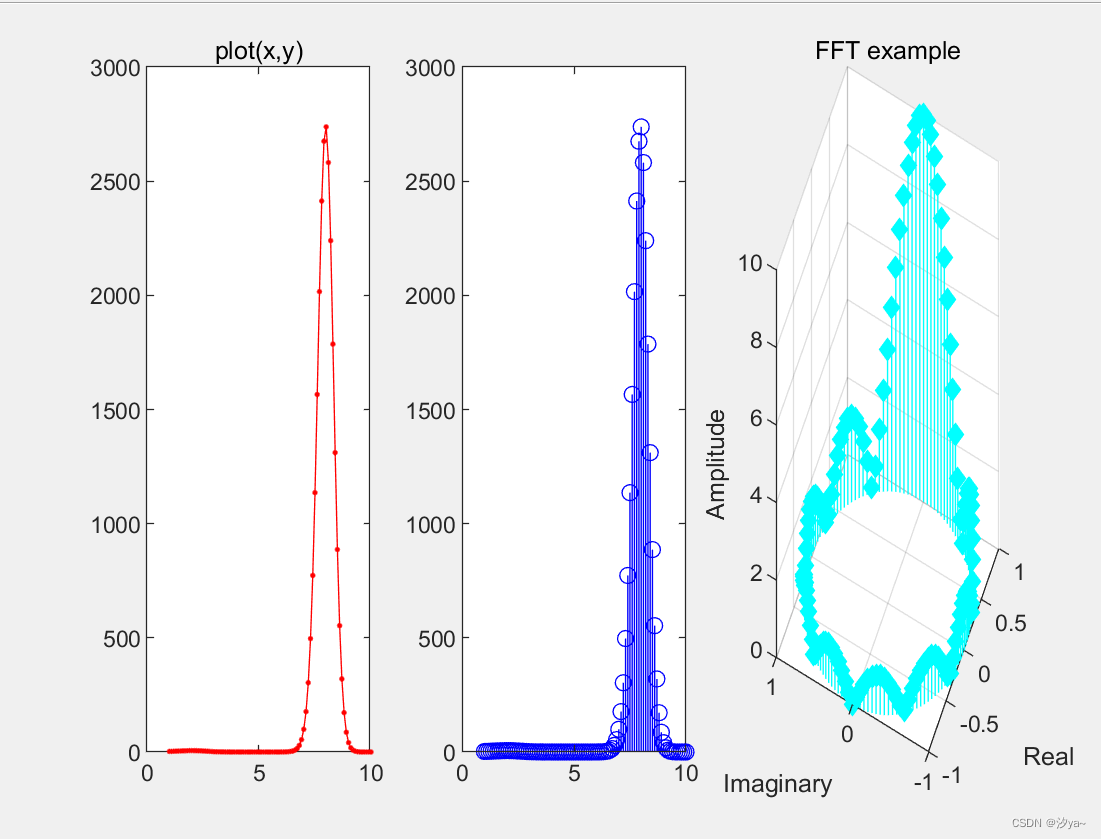
来源https://blog.csdn.net/LvzJason/article/details/122578671

二维曲线

反应两个变量的因果关系；

clear; clc; close all;

x = linspace(1, 200, 100); % 均匀生成数字1~200，共计100个
y1 = log(x) + 1; % 生成函数y = log(x) + 1
y2 = log(x) + 2; % 生成函数y = log(x) + 2

figure;
plot(x, y1); % 作图 y = log(x) + 1
hold on; % 多图共存在一个窗口上
plot(x, y2, 'LineWidth', 2); % 作图 y = log(x) + 2，LineWidth指线型的宽度，粗细尺寸2
hold off; % 关闭多图共存在一个窗口上

legend('y1', 'y2'); % 生成图例 y1 和 y2

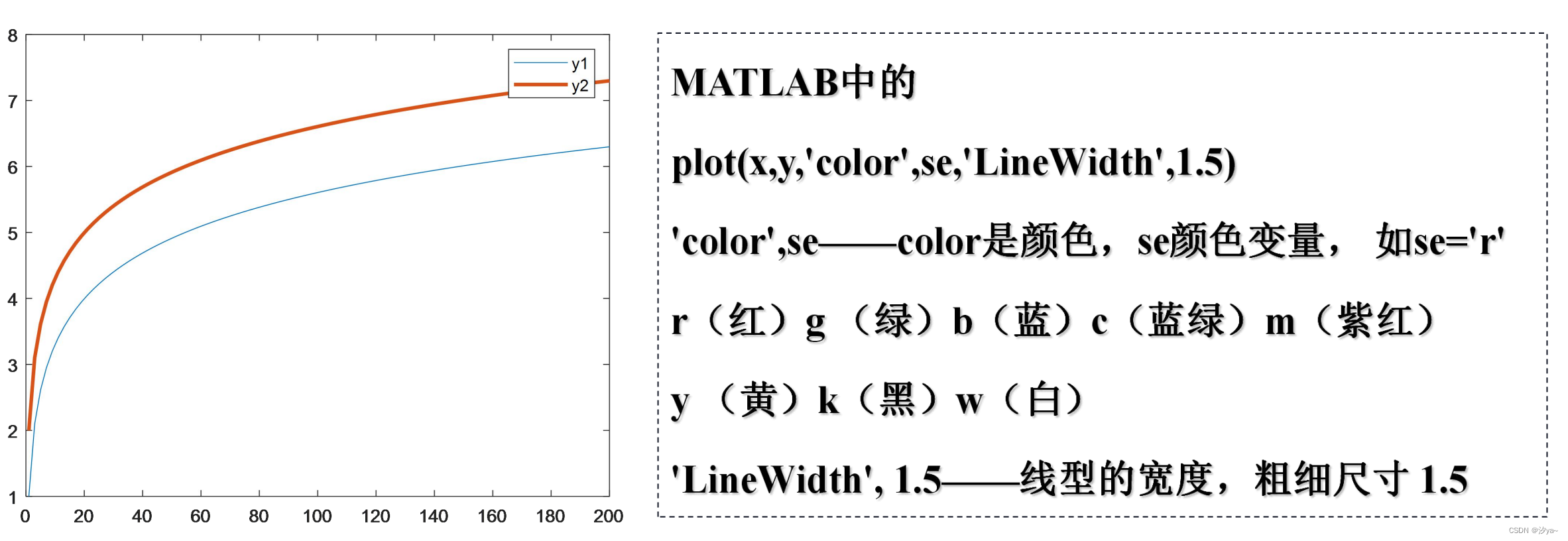
二维散点图

常用来比较理论数据和实验数据的趋势关系；

clear; clc; close all;

x = linspace(1, 200, 100); % 均匀生成数字1~200，共计100个
y1 = log(x) + 1; % 生成函数y = log(x) + 1
y3 = y1 + rand(1, 100) - 0.5; % 生成函数y = y1 + 随机数 - 0.5

figure;
plot(x, y1, 'LineWidth', 2, 'Color', [0.21, 0.21, 0.67]);
hold on;
% 设置数据点的形状、数据点的填充颜色、数据点的轮廓颜色
plot(x, y3, 'o', 'LineWidth', 2, 'Color', [0.46, 0.63, 0.90], ...
    'MarkerFaceColor', [0.35, 0.90, 0.89], 'MarkerEdgeColor', [0.18, 0.62, 0.17]);
hold off;

legend('y1', 'y3'); % 生成图例 y1 和 y3

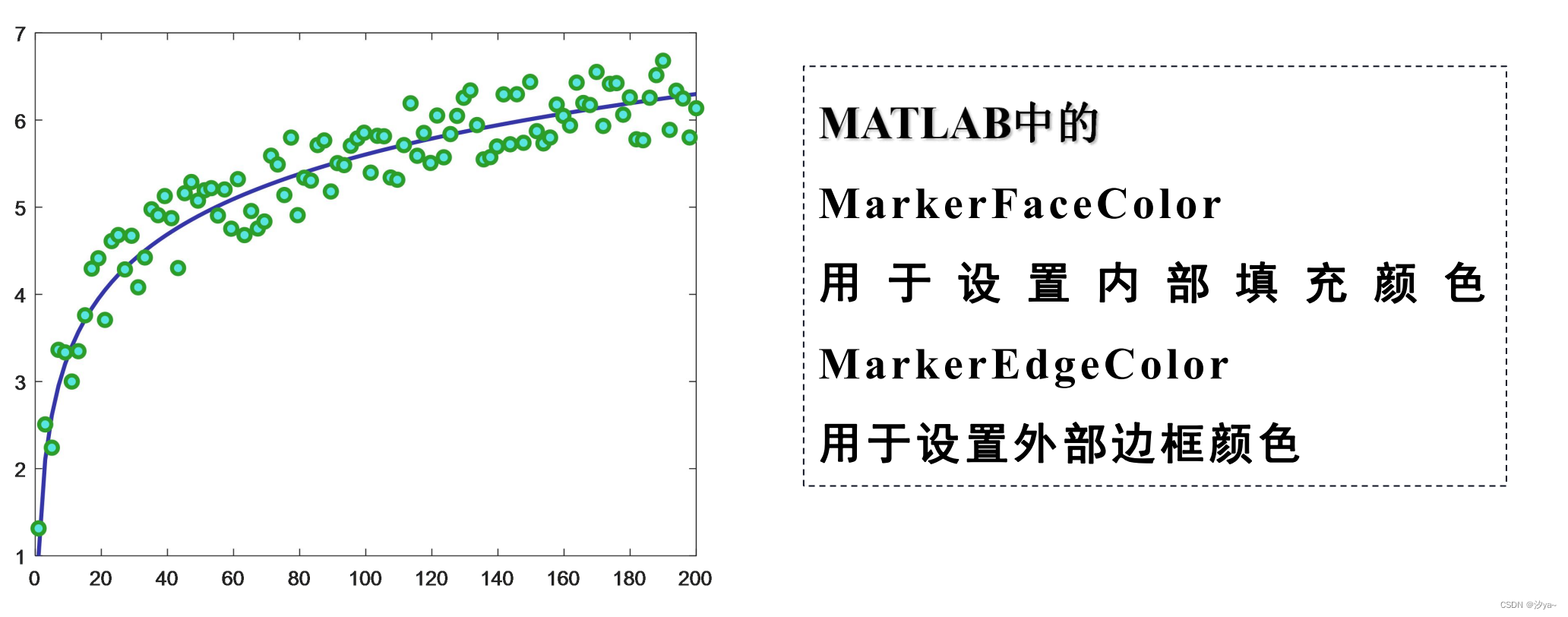
二维渐变图

用不同的颜色、数据点大小表征不同数值，更加直观

x = linspace(0, 3 * pi, 200);
y = cos(x) + rand(1, 200); % 随机生成1 * 200，位于[0, 1]的数字
sz = 25; % 尺寸为25
c = linspace(1, 10, length(x));
scatter(x, y, sz, c, 'filled');

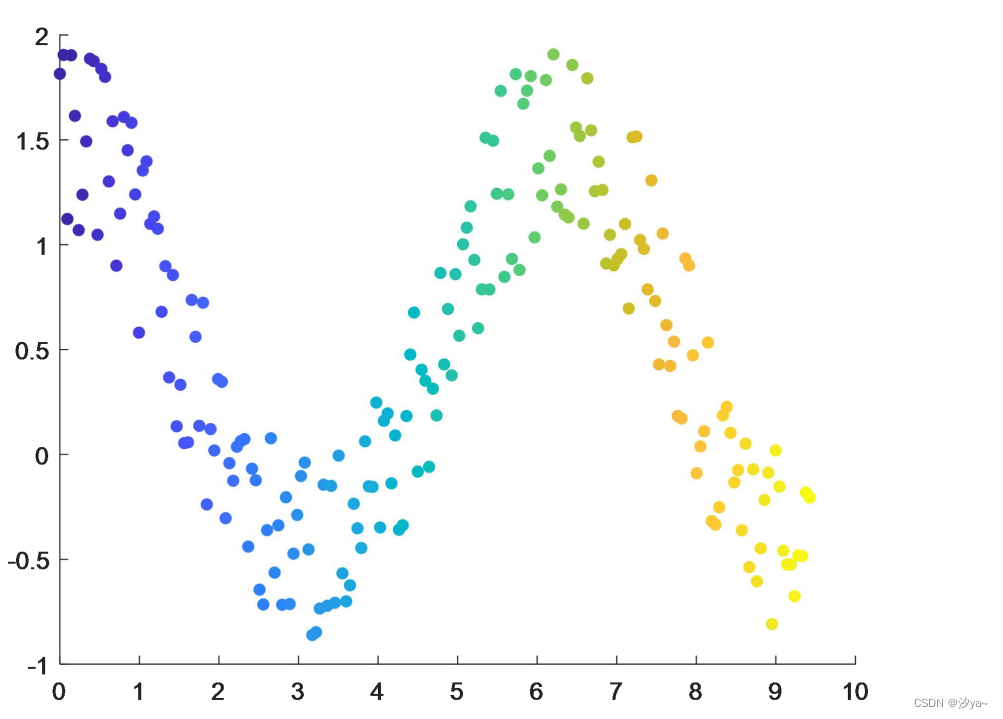
scatter函数用于创建散点图，其中可以通过不同的参数来指定散点的位置、大小和颜色。下面是scatter函数的用法概述：

1. scatter(x, y): 创建一个包含圆形标记的散点图，其中x和y是等长的向量，用于指定散点的位置。

2. scatter(x, y, sz): 指定圆的大小，sz可以是标量或向量，用于对所有圆或不同圆指定不同的大小。

3. scatter(x, y, sz, c): 指定圆的颜色，c可以是一个颜色名称（例如’red’）或RGB值（例如[0.5, 0.2, 0.8]），用于为所有圆或不同圆指定不同的颜色。

4. scatter(___,‘filled’): 使用’filled’选项填充圆，即将圆形标记填充为实心圆。

同时，scatter函数还支持在同一图像上绘制多组坐标，只需将x或y中的至少一个指定为矩阵即可。这样，就可以在散点图中绘制多组数据。

条形图

A = [60.689; 87.714; 143.1; 267.9515];
C = [127.5; 160.4; 231.9; 400.2];

B = C - A;
D = [A, B, C];

bar1 = bar([2:5:17], A, 'BarWidth', 0.2, 'FaceColor', 'k');
hold on;
bar2 = bar([3:5:18], B, 'BarWidth', 0.2, 'FaceColor', [0.5 0.5 0.5]);
bar3 = bar([4:5:19], C, 'BarWidth', 0.2, 'FaceColor', 'w');
hold off;

ylabel('耗时/s')
xlabel('GMM阶数')
legend('训练耗时', '测试耗时', '总耗时');
labelID = {'8阶', '16阶', '32阶', '64阶'};
set(gca, 'XTick', 3:5:20);
set(gca, 'XTickLabel', labelID);

填充图

x = 0.4:0.1:2*pi;
y1 = sin(2*x);
y2 = sin(x);

% 确定 y1 和 y2 的上下边界
maxY = max([y1; y2]);
minY = min([y1; y2]);

% 确定填充多边形, 按照顺时针方向来确定点
% fliplr 实现左右翻转
xFill = [x, fliplr(x)];
yFill = [maxY, fliplr(minY)];

figure
fill(xFill, yFill, [0.21, 0.21, 0.67]);
hold on

% 绘制轮廓线
plot(x, y1, 'k', 'LineWidth', 2)
plot(x, y2, 'k', 'LineWidth', 2)
hold off

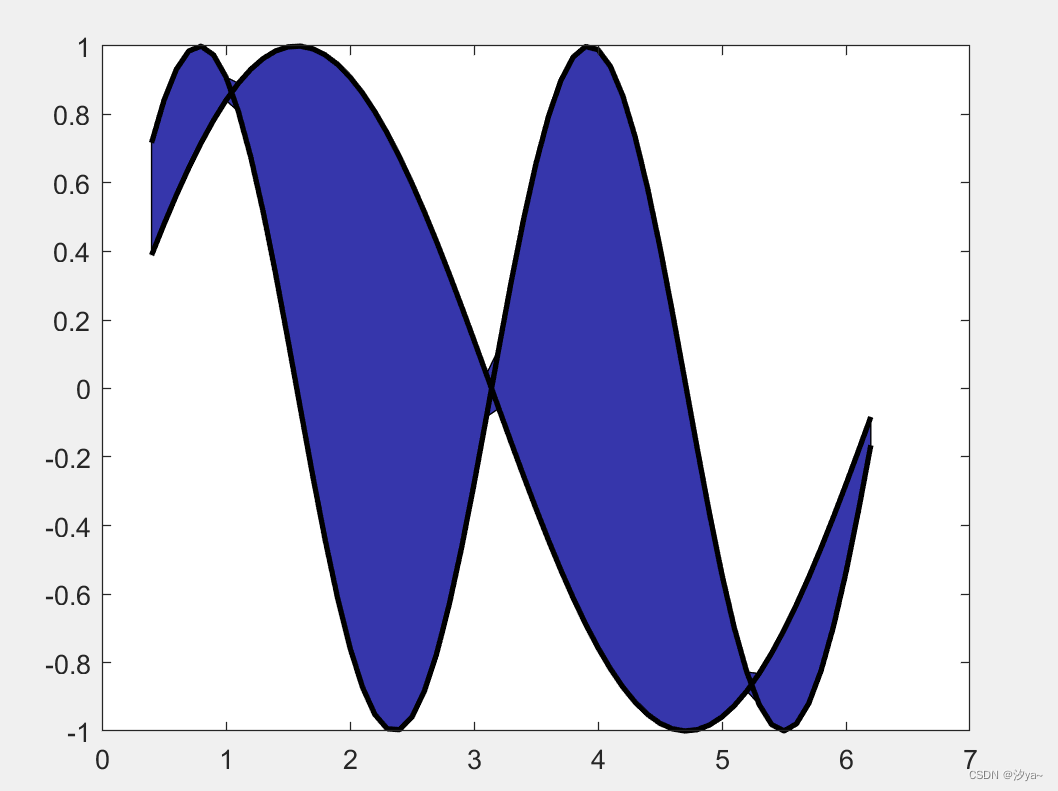
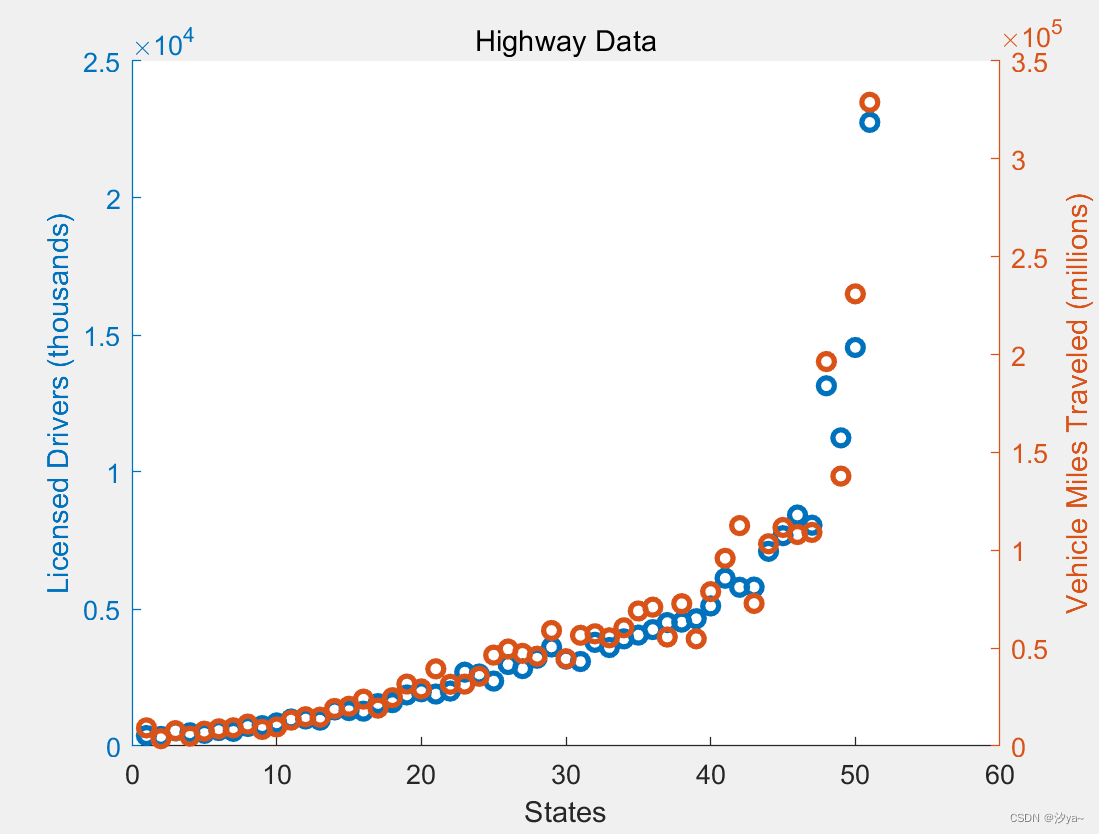
多Y轴图

figure; % 创建新的图像窗口

load('accidents.mat', 'hwydata'); % 加载'accidents.mat'文件中的'hwydata'变量

ind = 1:51; % 定义一个1到51的序列，用于表示州的编号

drivers = hwydata(:, 5); % 从'hwydata'中获取第5列数据，即'Licensed Drivers'

yyaxis left; % 使用左侧的y轴绘制第一个散点图
scatter(ind, drivers, 'LineWidth', 2); % 绘制散点图
title('Highway Data'); % 设置图像标题
xlabel('States'); % 设置x轴标签
ylabel('Licensed Drivers (thousands)'); % 设置左侧y轴标签

pop = hwydata(:, 7); % 从'hwydata'中获取第7列数据，即'Population'

yyaxis right; % 使用右侧的y轴绘制第二个散点图
scatter(ind, pop, 'LineWidth', 2); % 绘制散点图
ylabel('Vehicle Miles Traveled (millions)'); % 设置右侧y轴标签

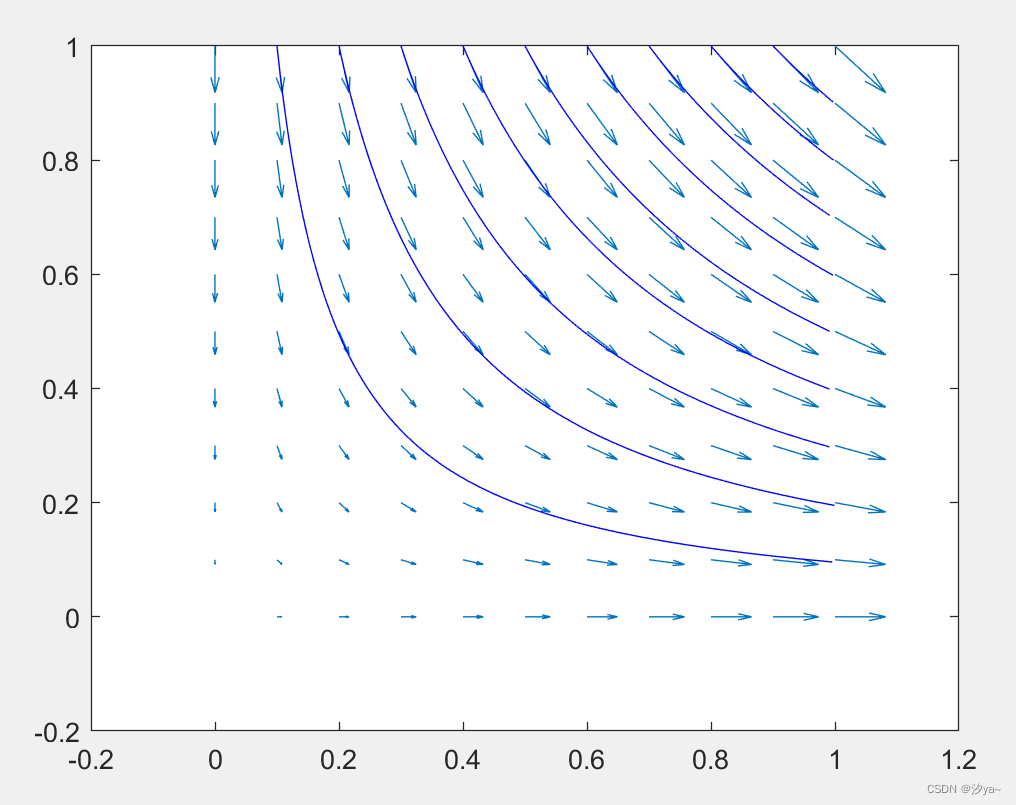
二维场图

% 直接拷贝streamline函数的帮助文档示例代码

% 生成网格点
[x, y] = meshgrid(0:0.1:1, 0:0.1:1);

% 定义矢量场
u = x;
v = -y;

% 定义流线的起点
startx = 0.1:0.1:0.9;
starty = ones(size(startx));

% 获取所有流线的属性
figure;
quiver(x, y, u, v); % 使用箭头来直观地显示矢量场
streamline(x, y, u, v, startx, starty); % 绘制流线

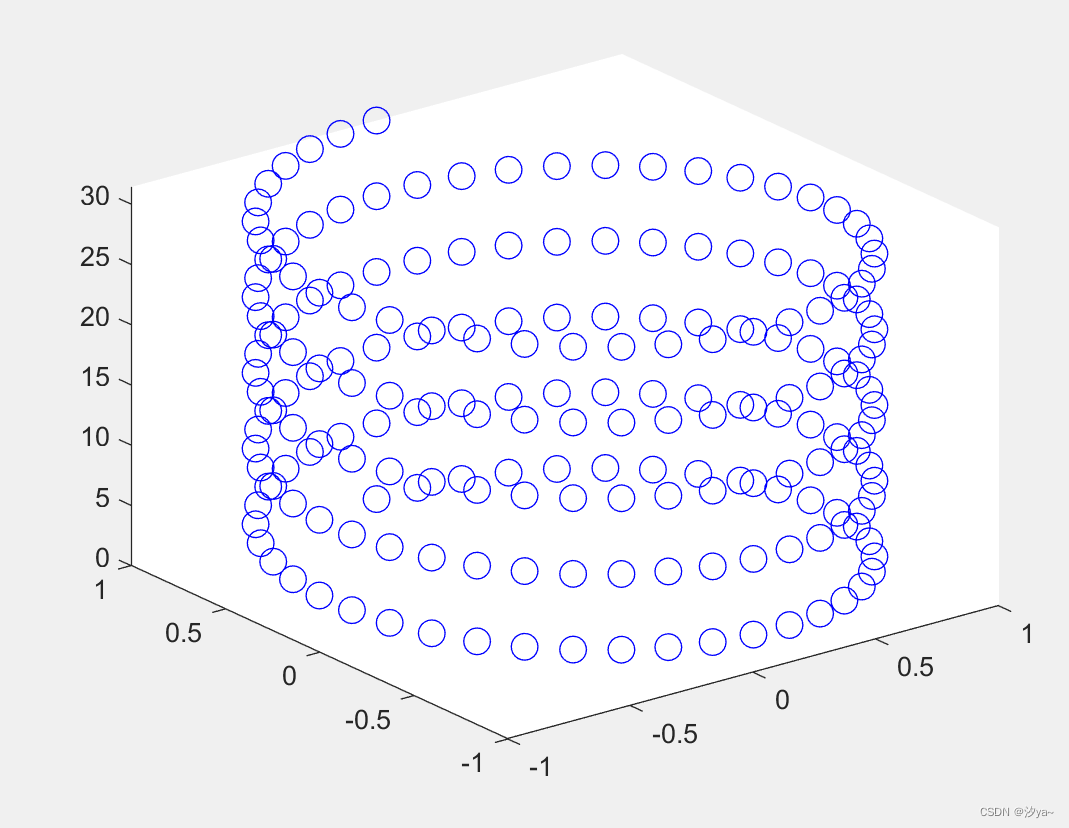
三维曲线图

figure;

t = 0:pi/20:10*pi;
xt = sin(t);
yt = cos(t);

plot3(xt, yt, t, 'o', 'Color', 'b', 'MarkerSize', 10);

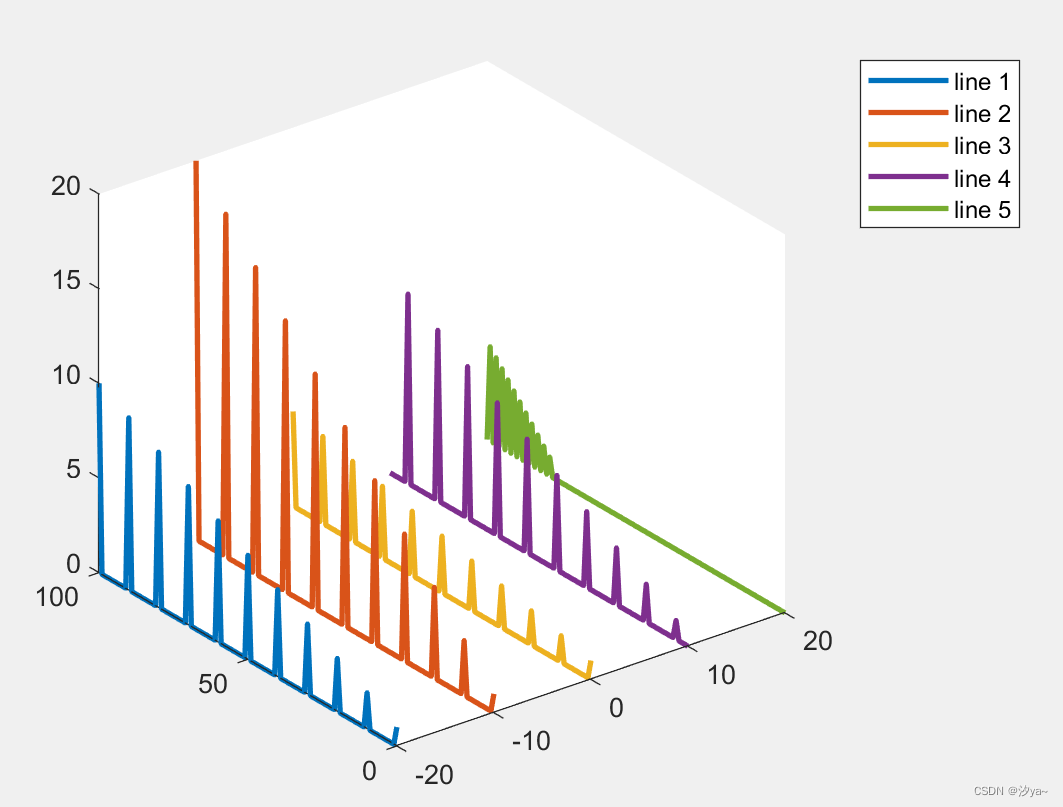
figure;

x = -20:10:20;
y = 0:100;

% 随便生成的 5 组数据, 也就是目标图上的 5 条曲线数据
z = zeros(5, 101);
z(1, 1:10:end) = linspace(1, 10, 11);
z(2, 1:10:end) = linspace(1, 20, 11);
z(3, 1:10:end) = linspace(1, 5, 11);
z(4, 5:10:end) = linspace(1, 10, 10);
z(5, 80:2:end) = linspace(1, 5, 11);

for i = 1:5
    % x 方向每条曲线都是一个值, 重复 y 的长度这么多次
    xx = x(i) * ones(1, 101);
    % z 方向的值, 每次取一条
    zz = z(i, :);
    % plot3 在 xyz 空间绘制曲线, 保证 x y z 长度一致即可
    plot3(xx, y, zz, 'LineWidth', 2);
    hold on
end
hold off

legend('line 1', 'line 2', 'line 3', 'line 4', 'line 5');

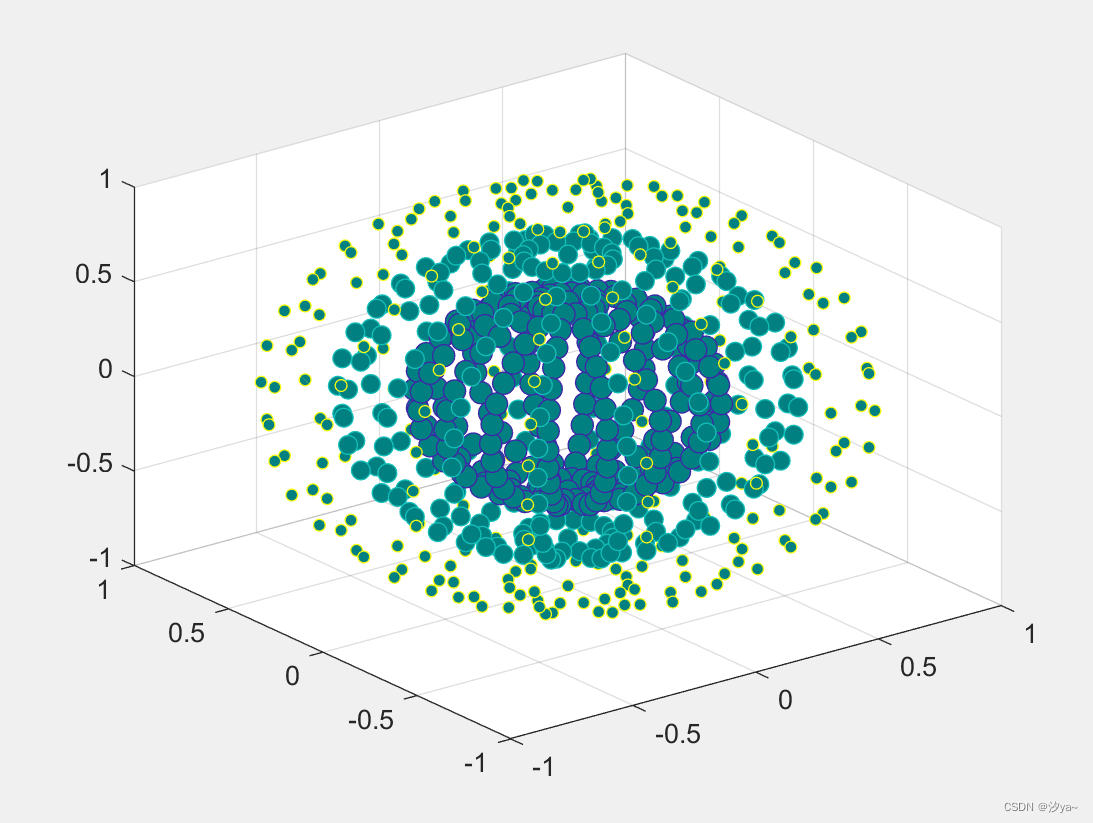
三维散点图

figure;

[X, Y, Z] = sphere(16); % 生成球体的网格数据

% 将球体数据沿着x、y、z方向分别缩放0.5、0.75和1.0倍，并展开成一维数组
x = [0.5 * X(:); 0.75 * X(:); X(:)];
y = [0.5 * Y(:); 0.75 * Y(:); Y(:)];
z = [0.5 * Z(:); 0.75 * Z(:); Z(:)];

S = repmat([70, 50, 20], numel(X), 1); % 复制大小信息
C = repmat([1, 2, 3], numel(X), 1); % 复制颜色信息

s = S(:); % 将大小信息展开成一维数组
c = C(:); % 将颜色信息展开成一维数组

h = scatter3(x, y, z, s, c); % 绘制散点图
h.MarkerFaceColor = [0, 0.5, 0.5]; % 设置散点的填充颜色为深青色

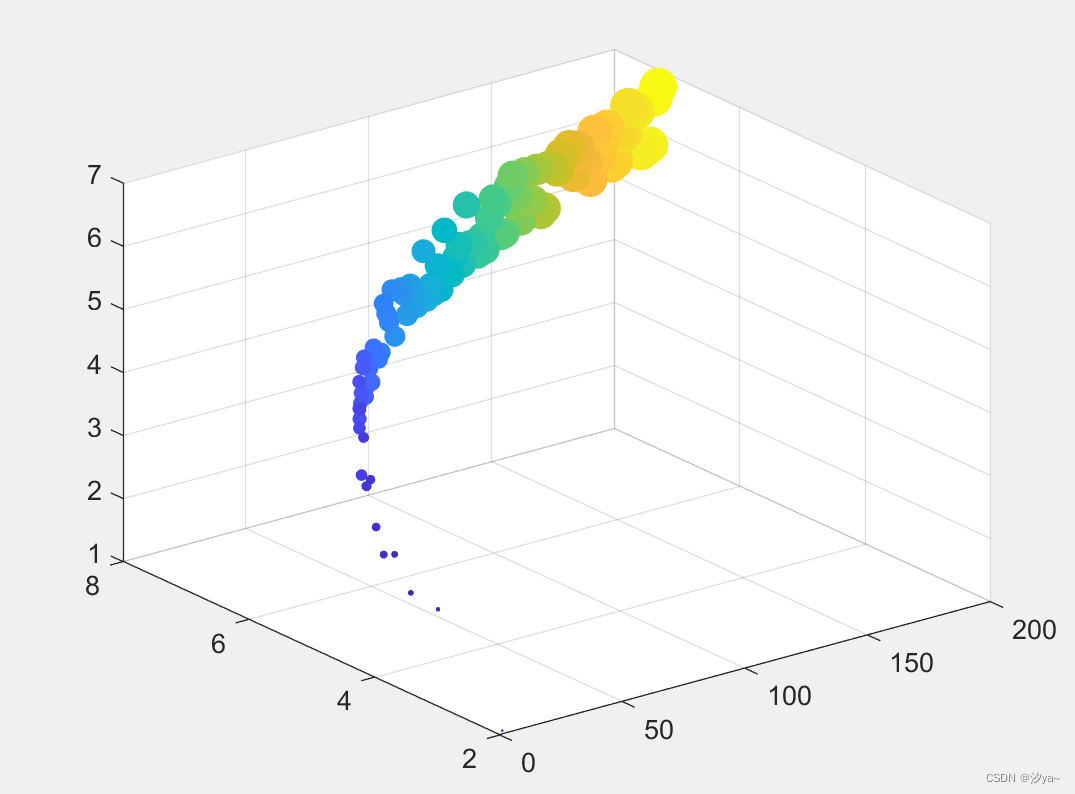
x = linspace(1, 200, 100); % 创建包含100个从1到200的均匀分布的数字的向量

y1 = log(x) + 1; % 计算y1向量，即log(x) + 1
y2 = log(x) + 2; % 计算y2向量，即log(x) + 2

y3 = y1 + rand(1, 100) - 0.5; % 计算y3向量，即y1加上一个随机误差，误差范围在-0.5到0.5之间

figure; % 创建新的图像窗口

% 使用scatter3函数绘制填充散点图
% x坐标为x向量，y坐标为y2向量，z坐标为y3向量
% 点的大小由x向量控制，点的颜色由x向量控制
% 'filled'参数指定填充点
scatter3(x, y2, y3, x, x, 'filled');

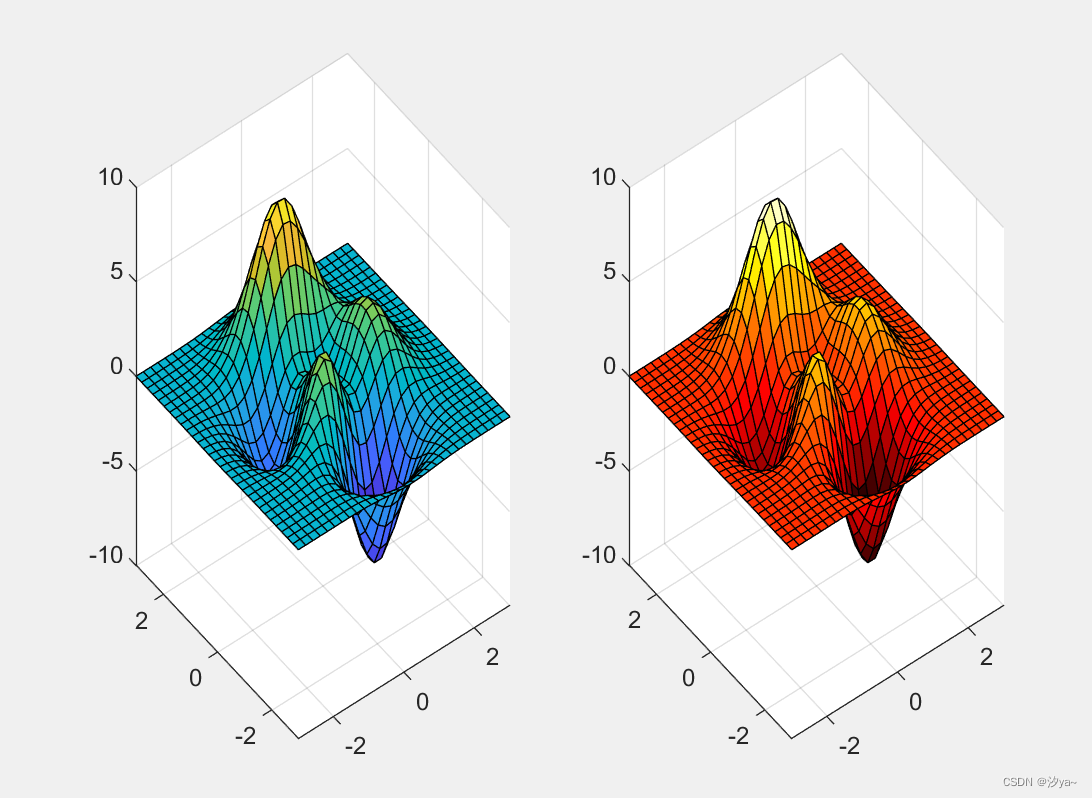
三维伪彩图

[x, y, z] = peaks(30); % 使用peaks函数生成一组数据，包含x、y、z三个变量

figure; % 创建新的图像窗口

% 绘制第一幅图
subplot(1, 2, 1); % 将图像划分为1行2列，并设置当前使用的子图为第1个子图
surf(x, y, z); % 使用surf函数绘制3D表面图

% 获取第一幅图的colormap，colormap默认为parula
plot1 = gca; % 获取当前子图的句柄，即第一幅图的句柄

subplot(1, 2, 2); % 将图像划分为1行2列，并设置当前使用的子图为第2个子图
surf(x, y, z); % 使用surf函数绘制3D表面图

% 设置第二幅图的颜色为hot colormap
colormap(hot);

% 设置第一幅图的颜色显示为parula colormap
colormap(plot1, parula);

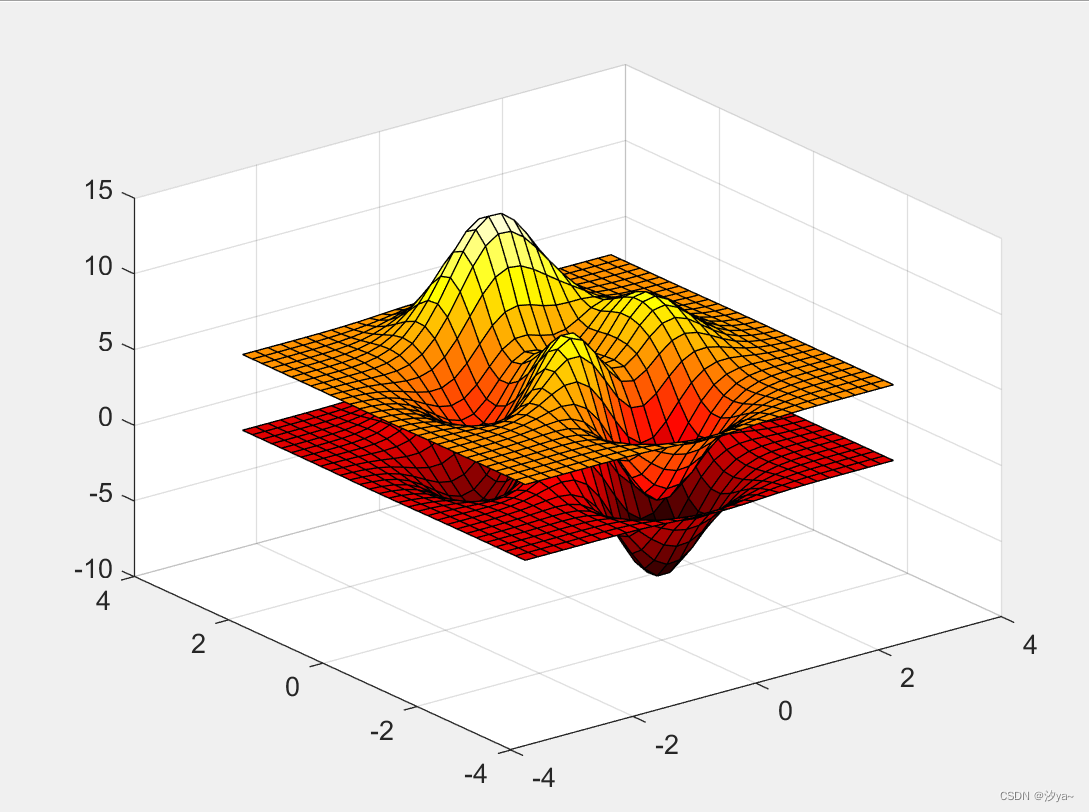
% 创建一个图像窗口
figure;

% 绘制第一个3D表面图
h1 = surf(x, y, z);

% 在同一张图上绘制第二个3D表面图，并将它在z方向上偏移5个单位
hold on
h2 = surf(x, y, z + 5);
hold off

% 设置颜色为hot colormap
colormap(hot);

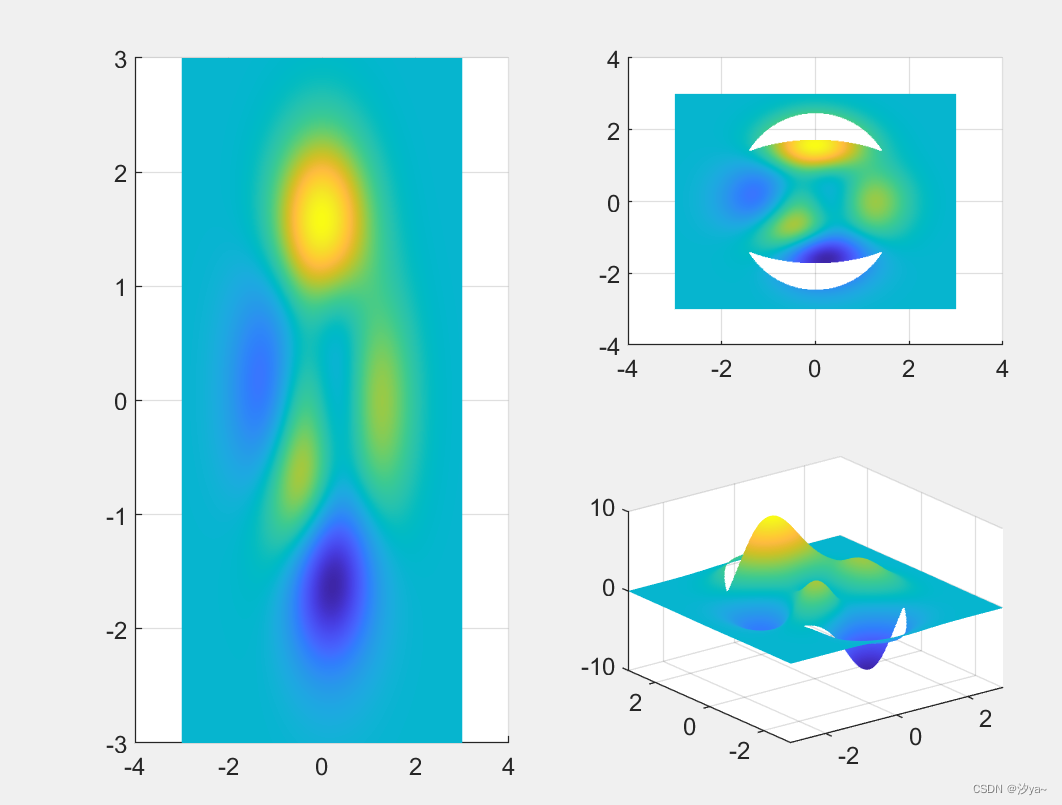
裁剪伪彩图

% 创建一个新的图像窗口
figure;

n = 300; % 设置n为300

% 生成peaks数据
[x, y, z] = peaks(n);

% 绘制第一个3D表面图
subplot(2, 2, [1, 3]); % 将图像划分为2行2列，并设置当前使用的子图为第1个和第3个子图
surf(x, y, z); % 使用surf函数绘制3D表面图
shading interp; % 设置渐变颜色
view(0, 90); % 设置视角为俯视

% 对数据进行处理
for i = 1:n
    for j = 1:n
        % 根据条件对z值进行修改
        if x(i, j)^2 + 2 * y(i, j)^2 > 6 && 2 * x(i, j)^2 + y(i, j)^2 < 6
            z(i, j) = NaN; % 若满足条件，则将对应位置的z值设置为NaN
        end
    end
end

% 绘制第二个3D表面图
subplot(2, 2, 2); % 将图像划分为2行2列，并设置当前使用的子图为第2个子图
surf(x, y, z); % 使用surf函数绘制3D表面图
shading interp; % 设置渐变颜色
view(0, 90); % 设置视角为俯视

% 绘制第三个3D表面图
subplot(2, 2, 4); % 将图像划分为2行2列，并设置当前使用的子图为第4个子图
surf(x, y, z); % 使用surf函数绘制3D表面图
shading interp; % 设置渐变颜色

等高线图

% 创建一个新的图像窗口
figure;

% 获取peaks数据
[X, Y, Z] = peaks;

% 绘制第一个等高线图
subplot(2, 2, 1); % 将图像划分为2行2列，并设置当前使用的子图为第1个子图
contour(X, Y, Z, 20, 'LineWidth', 2); % 使用contour函数绘制等高线图，20表示等高线的数量，LineWidth设置线宽

% 绘制第二个等高线图，使用虚线
subplot(2, 2, 2); % 将图像划分为2行2列，并设置当前使用的子图为第2个子图
contour(X, Y, Z, '--', 'LineWidth', 2); % 使用contour函数绘制虚线等高线图，LineWidth设置线宽

% 绘制第三个等高线图，显示指定等高线值
subplot(2, 2, 3); % 将图像划分为2行2列，并设置当前使用的子图为第3个子图
v = [1, 1]; % 指定等高线值
contour(X, Y, Z, v, 'LineWidth', 2); % 使用contour函数绘制等高线图，LineWidth设置线宽

% 生成新的数据并绘制第四个等高线图，显示等高线上的数值
x = -2:0.2:2; % 生成x数据
y = -2:0.2:3; % 生成y数据
[X, Y] = meshgrid(x, y); % 生成网格数据
Z = X .* exp(-X.^2 - Y.^2); % 计算z值
subplot(2, 2, 4); % 将图像划分为2行2列，并设置当前使用的子图为第4个子图
contour(X, Y, Z, 'ShowText', 'on', 'LineWidth', 2); % 使用contour函数绘制等高线图，并显示等高线上的数值，LineWidth设置线宽

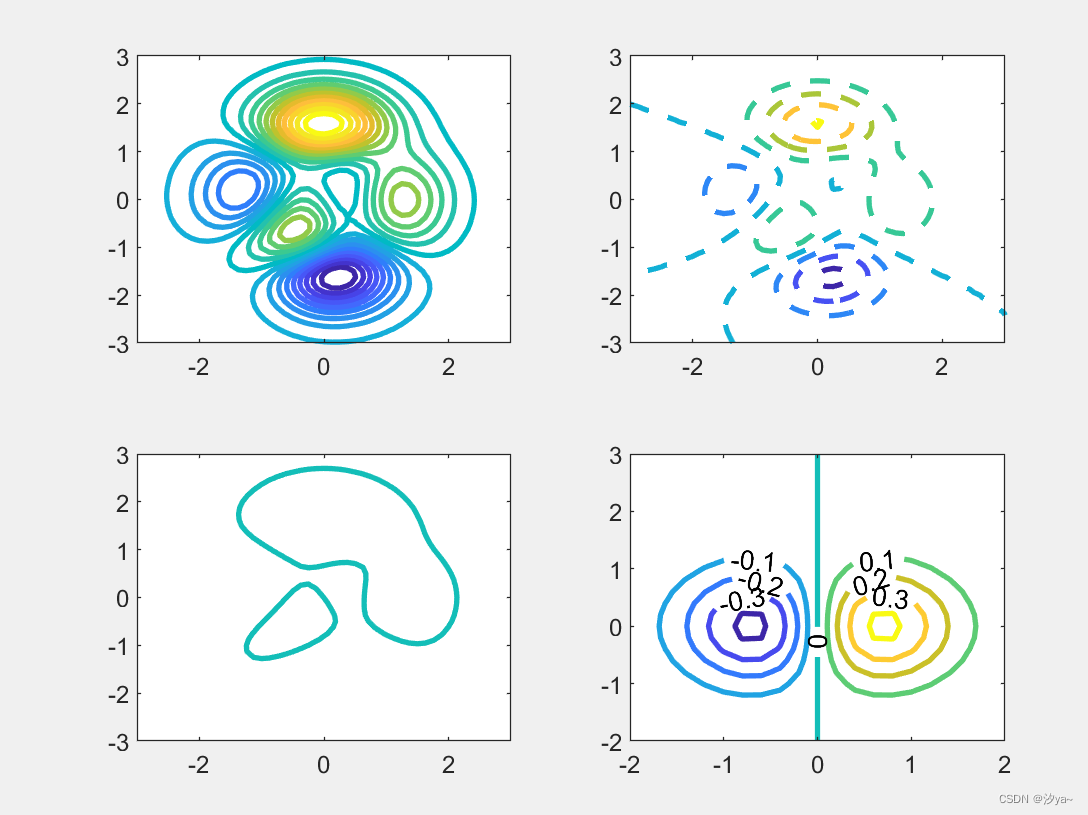
三维等高线图

% 创建一个新的图像窗口，并设置其位置为[0, 0, 900, 400]
figure('Position', [0, 0, 900, 400]);

% 绘制第一个3D等高线图
subplot(1, 3, 1); % 将图像划分为1行3列，并设置当前使用的子图为第1个子图
[X, Y, Z] = sphere(50); % 获取sphere数据
contour3(X, Y, Z, 'LineWidth', 2); % 使用contour3函数绘制3D等高线图，LineWidth设置线宽

% 生成新的数据并绘制第二个3D等高线图，显示指定等高线值和显示数值
[X, Y] = meshgrid(-2:0.25:2); % 生成x, y数据
Z = X .* exp(-X.^2 - Y.^2); % 计算z值
subplot(1, 3, 2); % 将图像划分为1行3列，并设置当前使用的子图为第2个子图
contour3(X, Y, Z, [-0.2, -0.1, 0.1, 0.2], 'ShowText', 'on', 'LineWidth', 2); % 使用contour3函数绘制3D等高线图，指定显示的等高线值和数值，LineWidth设置线宽

% 获取peaks数据并绘制第三个3D等高线图，显示指定等高线值
[X, Y, Z] = peaks; % 获取peaks数据
subplot(1, 3, 3); % 将图像划分为1行3列，并设置当前使用的子图为第3个子图
contour3(X, Y, Z, [2, 2], 'LineWidth', 2); % 使用contour3函数绘制3D等高线图，指定显示的等高线值和数值，LineWidth设置线宽

等高线填充图

% 创建一个新的图像窗口
figure;

% 绘制第一个等高线填充图
subplot(2, 2, 1); % 将图像划分为2行2列，并设置当前使用的子图为第1个子图
[X, Y, Z] = peaks(50); % 获取peaks数据
contourf(X, Y, Z); % 使用contourf函数绘制等高线填充图

% 绘制第二个等高线填充图，使用虚线
subplot(2, 2, 2); % 将图像划分为2行2列，并设置当前使用的子图为第2个子图
contourf(X, Y, Z, '--'); % 使用contourf函数绘制虚线等高线填充图，虚线样式由'--'指定

% 限定范围，并绘制第三个等高线填充图，显示指定等高线值和数值
subplot(2, 2, 3); % 将图像划分为2行2列，并设置当前使用的子图为第3个子图
contourf(X, Y, Z, [2, 3], 'ShowText', 'on'); % 使用contourf函数绘制等高线填充图，显示指定等高线值为[2, 3]，并显示等高线上的数值

% 绘制第四个等高线填充图，显示指定等高线值为[2, 2]
subplot(2, 2, 4); % 将图像划分为2行2列，并设置当前使用的子图为第4个子图
contourf(X, Y, Z, [2, 2]); % 使用contourf函数绘制等高线填充图，显示指定等高线值为[2, 2]

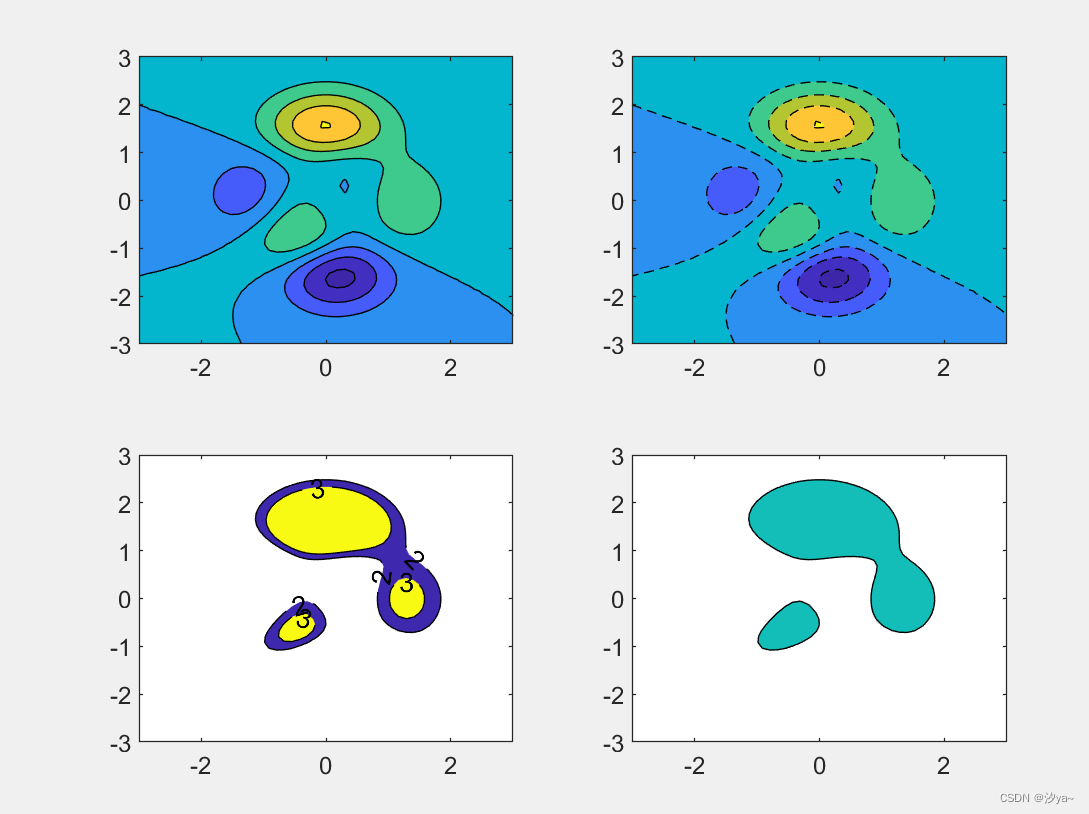
三维矢量场图

% 创建一个新的图像窗口
figure;

% 获取peaks数据
[X, Y, Z] = peaks(30);

% 计算曲面法线
[U, V, W] = surfnorm(X, Y, Z);

% 绘制矢量场
quiver3(X, Y, Z, U, V, W, 0.5, 'r');
hold on

% 绘制等高线曲面
surf(X, Y, Z);

% 设置x和y轴的显示范围
xlim([-3, 3]);
ylim([-3, 3.2]);

% 使用插值填充曲面
shading interp

hold off

% 设置视角为俯视图
view(0, 90);

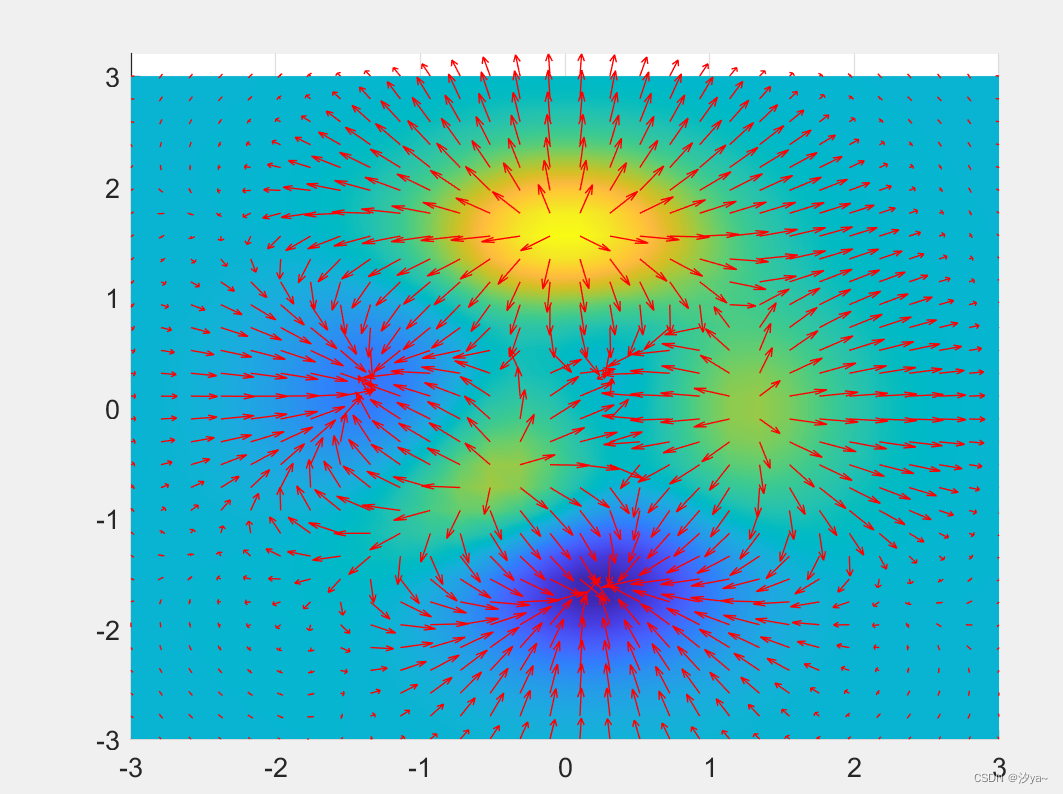
伪彩图+投影图

% 清除工作区、命令窗口和关闭所有图形窗口
clear; clc; close all;

% 生成坐标向量 x 和 y
x = linspace(-3, 3, 30);
y = linspace(-4, 4, 40);

% 生成网格 X 和 Y
[X, Y] = meshgrid(x, y);

% 计算 peaks 函数的 Z 值
Z = peaks(X, Y);

% 部分区域置零
Z(5:10, 15:20) = 0;

% 计算 Z 的最大值
z1 = max(Z);

% 计算 Z 每行的最大值
z2 = max(Z, [], 2);

% 创建新的图像窗口，并划分为 3x3 的子图区域
figure;
subplot(3, 3, [1, 2]); % 第一行第一和第二个子图
plot(x, z1, 'LineWidth', 2);

subplot(3, 3, [6, 9]); % 第三行第一和第三个子图
plot(z2, y, 'LineWidth', 2);

subplot(3, 3, [4, 5, 7, 8]); % 第二行第一、第二、第四个子图
surf(x, y, Z); % 绘制 peaks 函数的三维图像

xlim([-3, 3]); % 设置 x 轴的显示范围
ylim([-4, 4]); % 设置 y 轴的显示范围
view(0, 90); % 设置视角为俯视图
shading interp; % 平滑图像

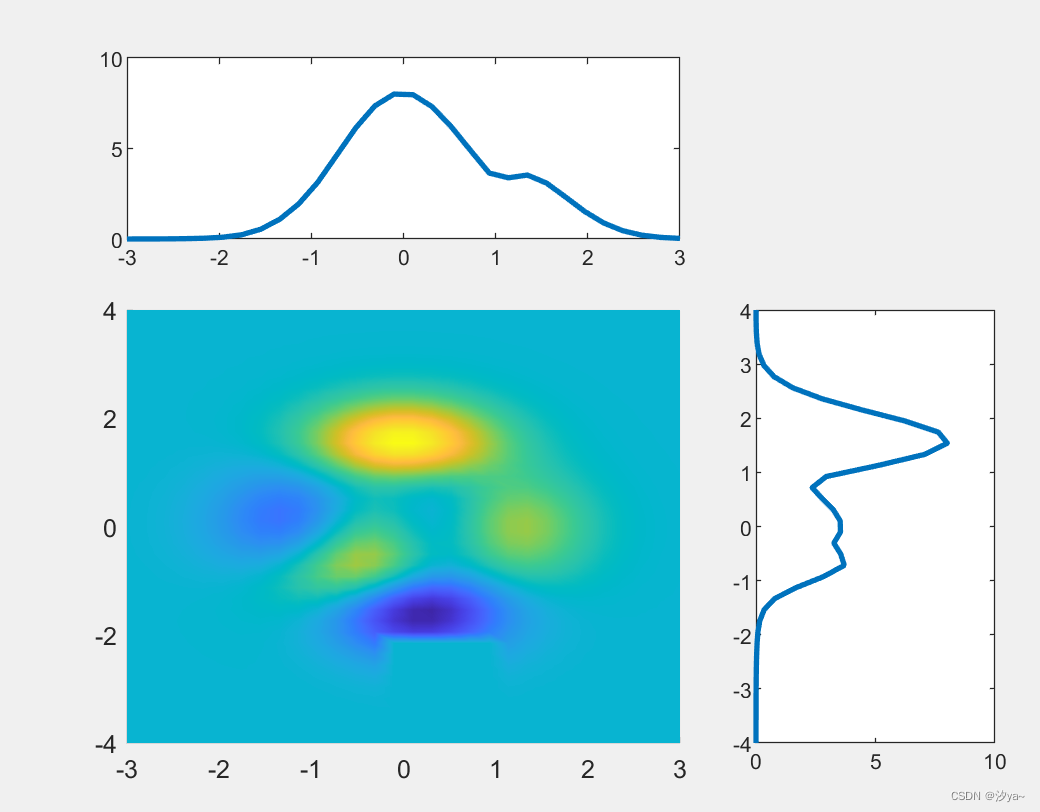
热图

% 清除工作区和命令窗口
clear; clc;

% 生成大小为 50x50 的随机矩阵 z
z = rand(50);

% 将 z 的元素根据阈值替换为指定值
z(z >= 0.0 & z < 0.6) = 0.5;
z(z >= 0.6 & z < 0.8) = 0.7;
z(z >= 0.8 & z <= 1) = 0.9;

% 将部分元素设置为 NaN
for i = 1:30
    z(randi(50, 1, 1):end, i) = nan;
end

for i = 31:50
    z(30 + randi(20, 1, 1):end, i) = nan;
end

% 将指定区域设置为 NaN
z(20:25, 40:45) = nan;

% 创建新的图像窗口
figure;

% 使用 pcolor 绘制伪彩色图像，并获取绘图对象 ax
ax = pcolor(z);

% 设置视角为俯视图
view(0, 90);

% 设置边界线颜色为白色
ax.EdgeColor = [1, 1, 1];

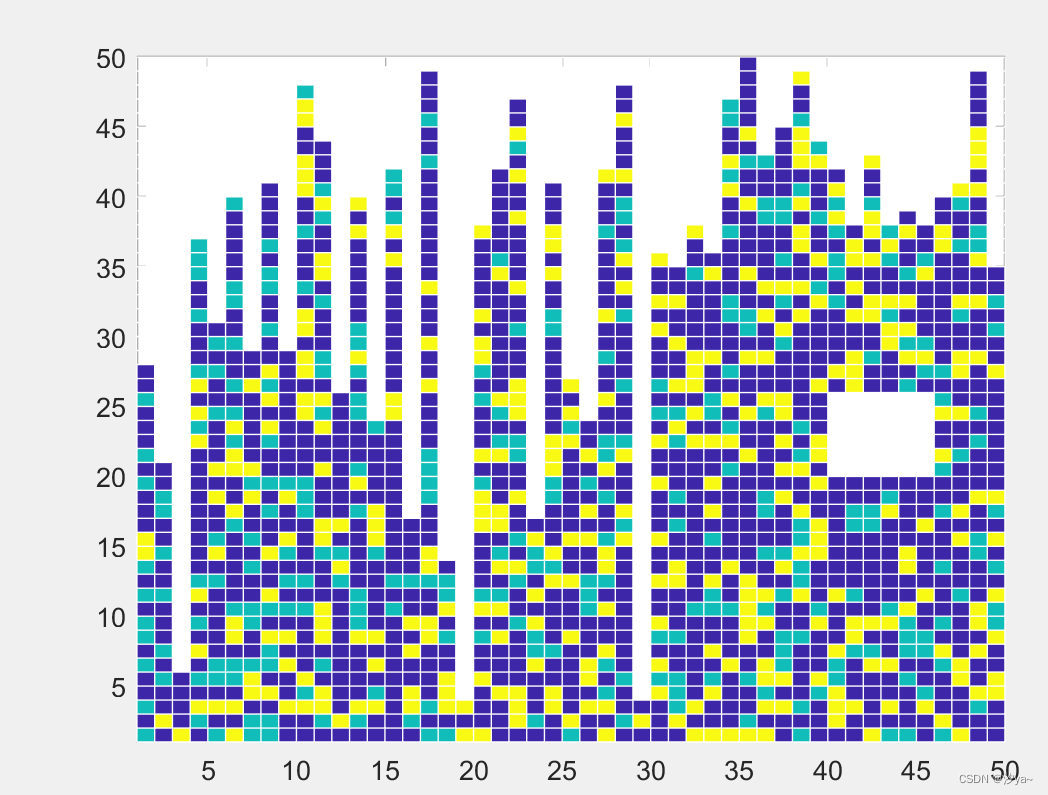
分子模型图

% 清除工作区和命令窗口
clear; clc;

% 生成球面的坐标信息，将球面分为 100 个点
[x, y, z] = sphere(100);

% 大球的缩放比例
C = 10;

% 小球的缩放比例
H = 5;

% 创建新的图像窗口
figure;

% 绘制大球，红色，无边界线
surf(C * x, C * y, C * z, 'FaceColor', [0.5 0 0], 'EdgeColor', 'none');
hold on

% 绘制四个小球，都稍微偏离一点位置，准确位置需要计算
% 这里只是演示一个大致位置
surf(H * x, H * y, H * z + 10, 'FaceColor', [0 0 0.5], 'EdgeColor', 'none');
surf(H * x + 10, H * y, H * z - 3, 'FaceColor', [0 0 0.5], 'EdgeColor', 'none');
surf(H * x - 4, H * y - 10, H * z - 3, 'FaceColor', [0 0 0.5], 'EdgeColor', 'none');
surf(H * x - 4, H * y + 10, H * z - 3, 'FaceColor', [0 0 0.5], 'EdgeColor', 'none');

% 设置坐标轴相等并关闭显示
axis equal off;

% 添加光源，增加立体感
light;

% 关闭光照效果
lighting none;

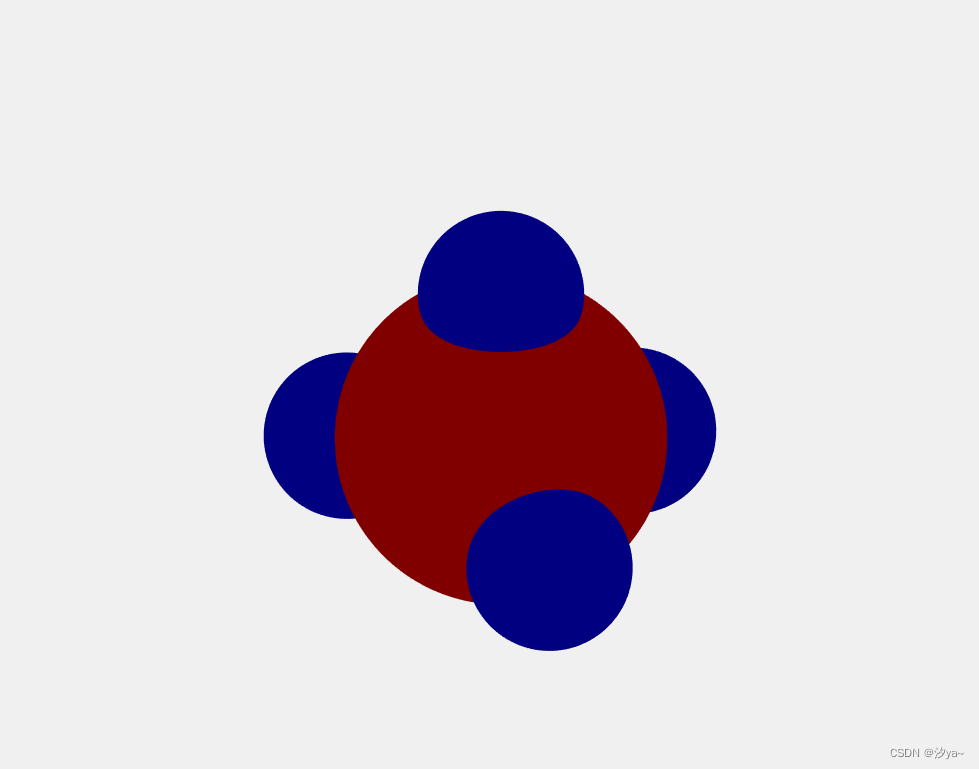
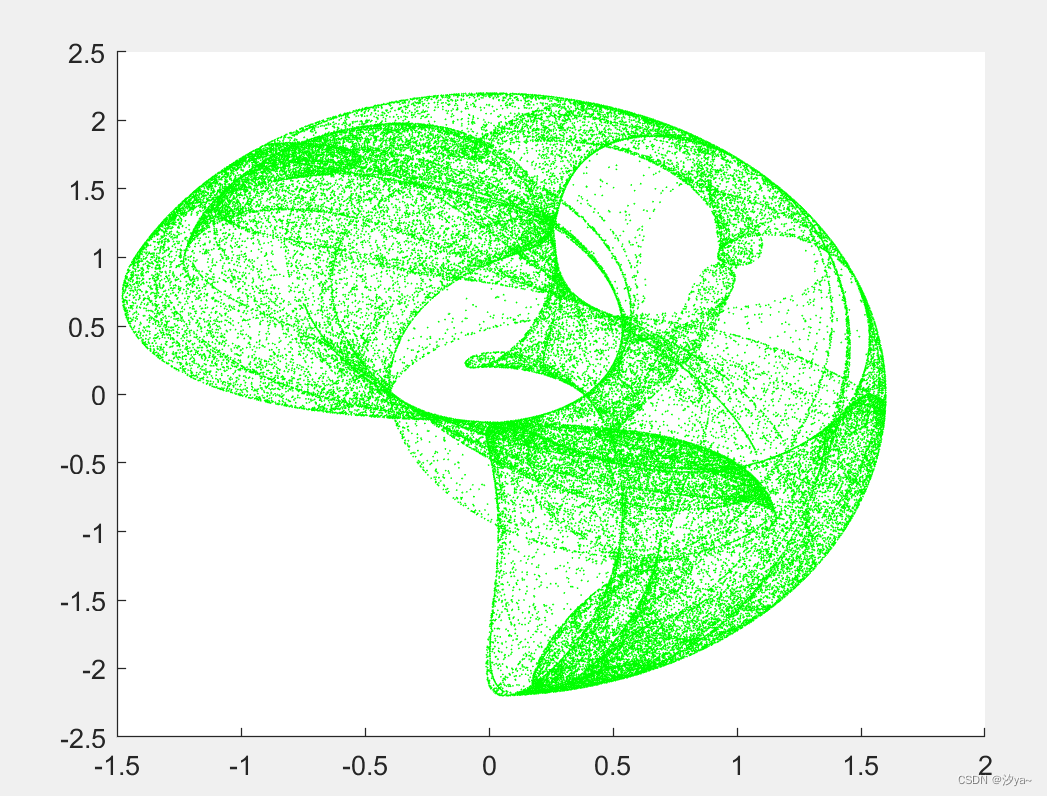
分形图

clear;

% 不同的参数有不同的图形
a = 1.7; b = 1.7; c = 0.6; d = 1.2; % 可根据需要选择不同的参数组合
% a = 1.5; b = -1.8; c = 1.6; d = 0.9;

x = 0; y = 0; % 初始化 x 和 y

n = 100000; % 迭代次数，这里增加到 10000000

kx = zeros(1, n); % 存储 x 的迭代结果
ky = zeros(1, n); % 存储 y 的迭代结果

% 迭代循环
for i = 1:n
    % 计算新的 x 和 y 值
    temp_x = sin(a * y) + c * cos(a * x);
    temp_y = sin(b * x) + d * cos(b * y);
    
    % 存入数组
    kx(i) = temp_x;
    ky(i) = temp_y;
    
    % 重新赋值 x, y
    x = temp_x;
    y = temp_y;
end

% 绘制散点图
scatter(kx, ky, 0.1, 'green');

MATLAB轻松绘制地图路线——已知及未知坐标

https://blog.csdn.net/wayne6515/article/details/112647925