基于遗传算法的试题组卷（一）

news2024/9/28 5:24:31

基于遗传算法的试题组卷
IT企业每年都会在春季和秋季举行校园招聘，对于个性化定制的试卷需求量很大，如何组出又好又快的定制化试题对于IT企业非常重要。组卷技术主要针对知识点覆盖率，题型，难度系数，试题数量等一些试题的属性进行多条件约束优化组卷。

为了方便考官出题考试，系统中引入了试题组卷技术。如何又快又好地生成符合考官口味的试卷变得非常关键。下面将对一些常用的组卷算法进行介绍。

目前常用的组卷有随机选取法，回溯试探法，遗传算法三种。

随机选取法：根据状态空间的控制指标，由计算机随机的抽取一道试题放入试题库，此过程不断重复，直到组卷完毕，或已无法从题库中抽取满足控制指标的试题为止。该方法结构简单，对于单道题的抽取运行速度较快，但是对于整个组卷过程来说组卷成功率低，即使组卷成功，花费时间也令人难以忍受。尤其是当题库中各状态类型平均出题量较低时，组卷往往以失败告终。

回溯试探法：这是将随机选取法产生的每一状态记录下来，当搜索失败时释放上次记录的状态类型，然后再依据一定的规律变换一种新的状态类型进行试探，通过不断的回溯试探直到试卷生成完毕或退回出发点为止，这种有条件的深度优先算法，对于状态类型和出题量都较少的题库系统而言，组卷成功率较好，但是对于程序结构相对比较复杂，该算法表现就比较差了。

遗传算法：遗传算法（Genetic Algorithm）是借鉴生物界中的自然选择和自然遗传等生物进化论的内容而提出的一种搜索算法。算法主要用来处理多约束的近似最优解。得到的结果取决于繁衍的代数，适应度函数的计算等。遗传算法主要包括如下几个阶段：初始化阶段，选择阶段，交叉阶段，变异阶段，验收阶段。在试题的组卷过程中会有很多约束条件如难度，题型，试题数量等多种因素，因此比较适合用遗传算法进行组卷。

3.2 遗传算法

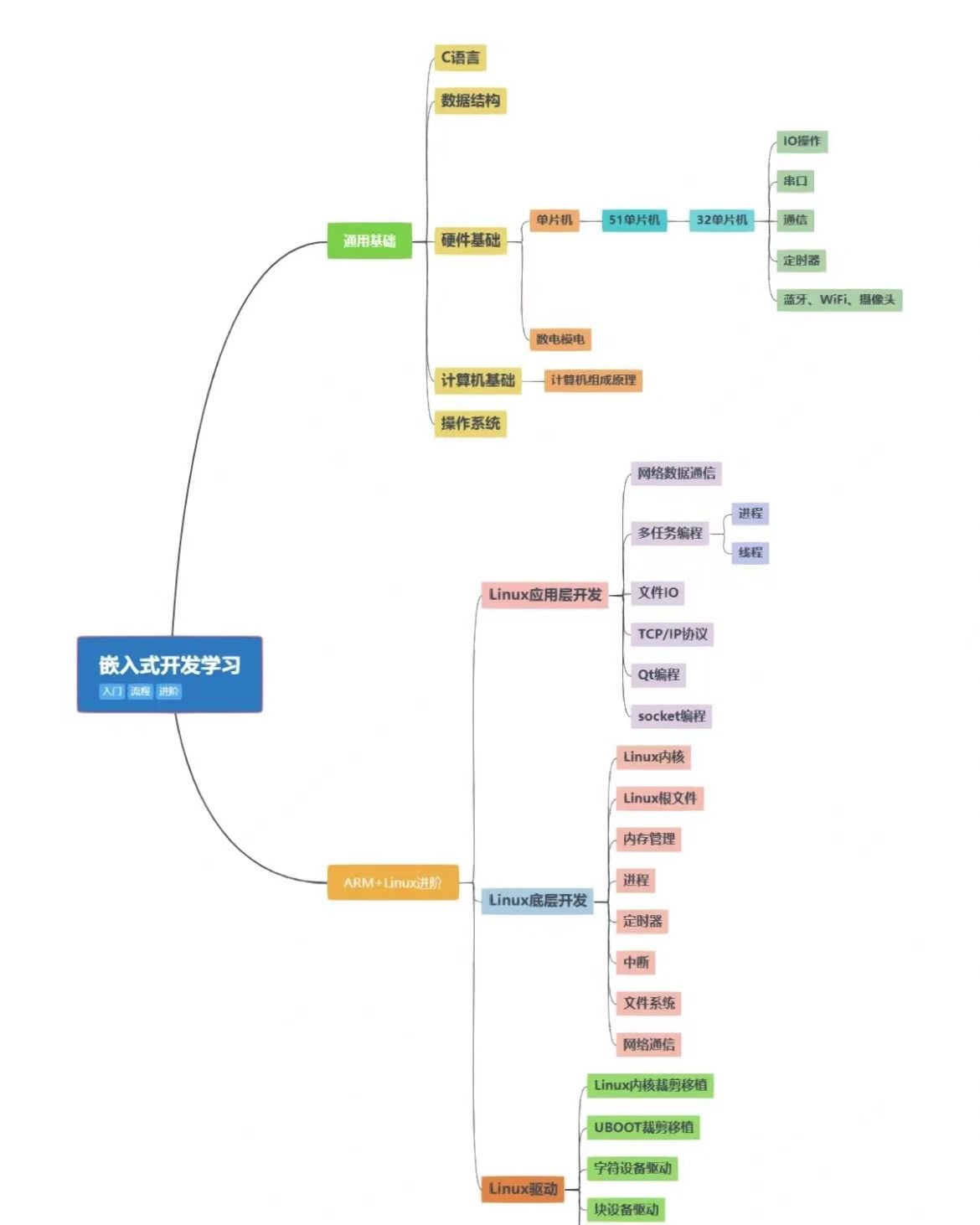
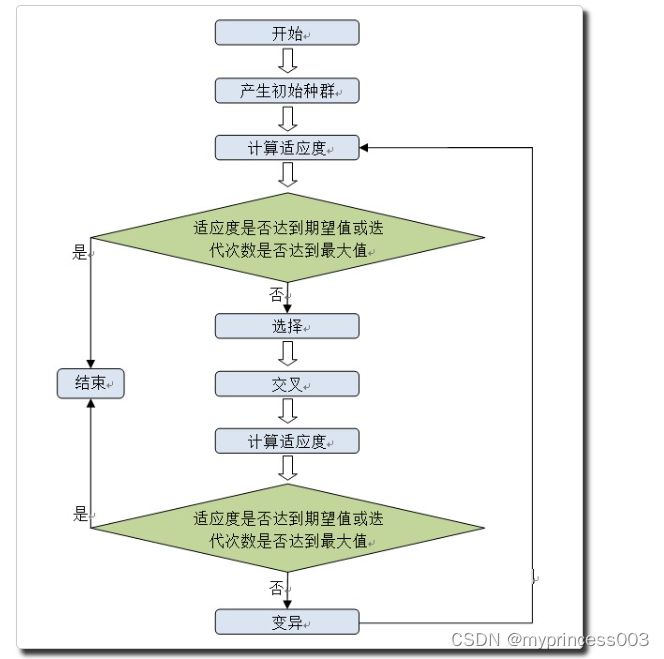
遗传算法（Genetic Algorithm）是借鉴生物界中的自然选择和自然遗传等生物进化论的内容而提出的一种搜索算法。遗传算法的大体流程如下

在这里插入图片描述

图3-1 遗传算法的基本过程

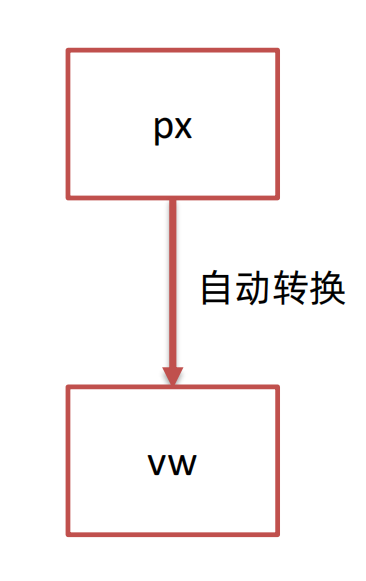
初始化阶段：确定染色体的形式。先选择一种方式对x进行编码，使其从实际的解空间(phenotype space)被映射到编码空间(genotype space),也就是把实数x变成一条染色体。一般有两种编码方式，实数编码和二进制编码，各具优缺点。实数编码，直接用实数表示基因，容易理解且不需要解码过程，但容易过早收敛，从而陷入局部最优。二进制编码，稳定性高，种群多样性大，但需要的存储空间大，需要解码且难以理解确定好染色体形式之后，我们便可以拿它生成一个初始的种群。

选择阶段：选择阶段经历了适应性选择和随机选择。在适应性选择中，我们通过适应性函数(fitness function)对种群中的每一条染色体进行适应性评估，按评估结果对染色体进行排序。筛选出适应性最好的一定数量（可以通过参数调节）的染色体，作为下一代的父母加入存货列表。而在随机选择中，我们会随机挑选一些没有通过适应性选择的个体也加入存活列表，这样做是为了使得一些拥有潜在价值基因但适应性很差的个体得以生存下来。

交叉阶段：每一代染色体的数量是一定的，我们淘汰了一部分染色体，就要生成新的染色体来补足空缺。从上一代中，我们保留了一部分存活的染色体，它们之间将会进行交叉。交叉是指随机从存活列表中抽取两个染色体，将这两条染色体进行融合从而生成新的染色体（就是取一部分父染色体的基因，再在母染色体取在父染色体没有取到的基因，把这些基因合成一条新的染色体），把新的染色体加入种群中。交叉操作会一直持续，直到种群数量跟之前的种群数量相同。常见的交叉策略有重复交叉最优保留策略、混合交叉策略、随机基因交叉策略。

变异阶段：对于种群中的每一条染色体，使其一定几率地发生随机变异。常见的变异策略有自适应变异、多变异。

3.3.1 试卷约束目标
将一份试卷映射为一个染色体，组成试卷的每个试题映射为一个基因向量。每一道都有多个属性，这些属性构成了试卷的约束条件。论文对于试题的约束属性如下表所示
在这里插入图片描述
3.3.2 试题编解码设计
由于试题的数量较多，不适合采用二进制进行编码，决定采用实数进行编码。试题的ID就是实数的编码值。将一整份试卷作为一个染色体，试题作为染色体上的基因。染色体进行分段处理，每一个段作为一个题型，这样可以保证每种题型的数据不会发生变化。比如要组一套《软件开发工程师的招聘试卷》，其中选择题3道，简答题4道，编程题2道，染色体的编码如下：
在这里插入图片描述
3.3.3 种群初始化设计
通过随机的方法对种群进行初始化。