文章目录
- 概念
- 插入和删除
- 非递归实现中的问题
- 递归中的引用简化
- 相关OJ复习直达
概念
由下面二叉搜索树的性质可以知道,中序遍历它便可以得到一个升序序列,查找效率高,小于往左找,大于往右走。最多查找高度次,走到到空,还没找到,这个值不存在
插入和删除
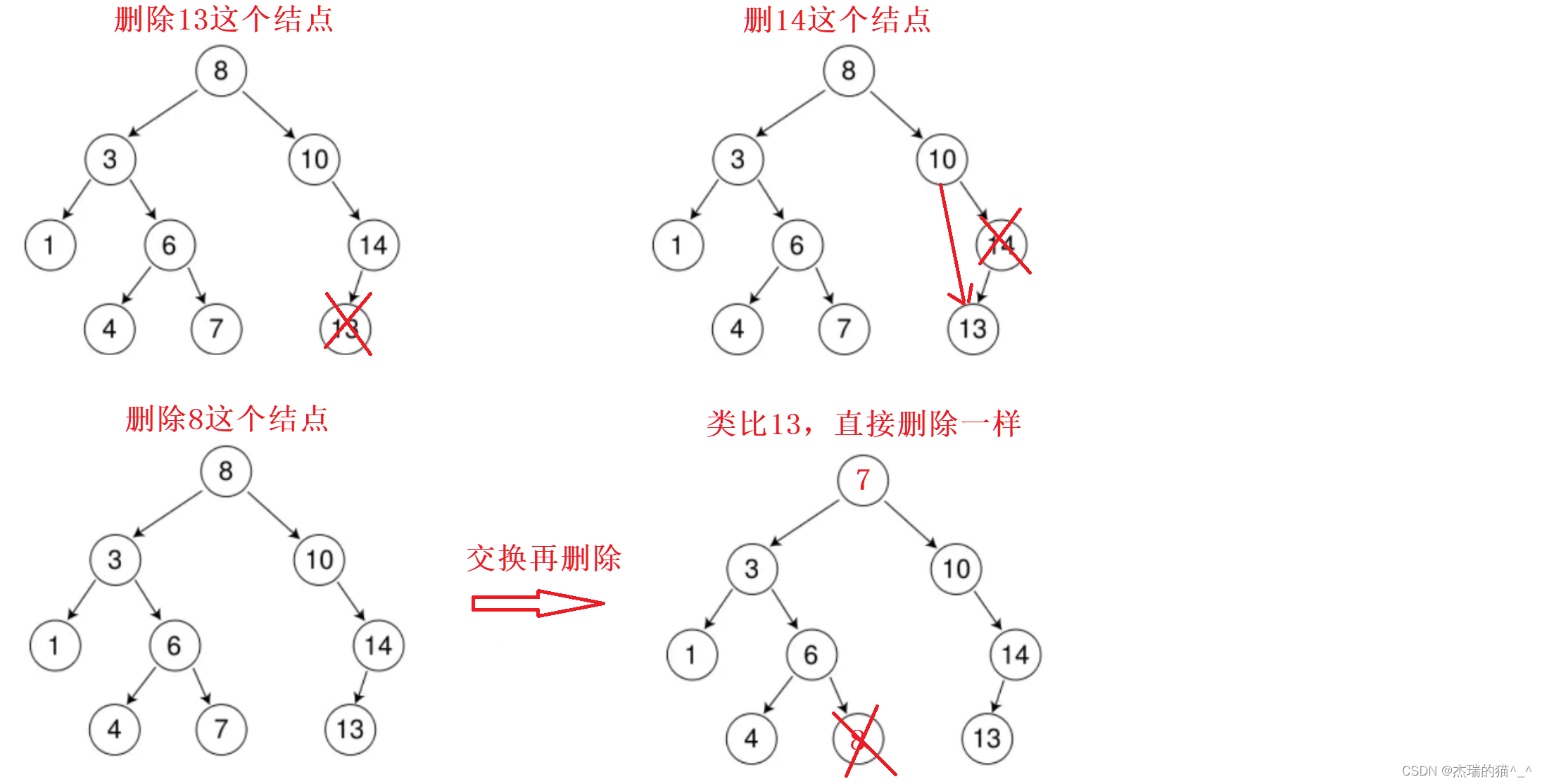
替换法,即找该删除结点中左子树中的最大结点或者右子树的最小结点,进行替换,再删除该结点,这样可以保证二叉树的搜索性,使该结点删除后,还是二叉搜索树
非递归实现中的问题
下面这里删除13和14都是属于同一类型,13的左孩子为nullptr则,让13的父亲指向13的右孩子。删除14的时候,14的左孩子不为nullptr,则让14的父亲指向14的左孩子。这里很明显我们要记录删除结点的父结点,同时,还要判断删除结点是父节点的左孩子还是右孩子。若删除的孩子有左右孩子,那么我们的先找个孩子替换它,这个孩子必须是左子树的最大孩子,或者右子树的最小孩子,再像删除13和14一样删除这个结点
递归中的引用简化
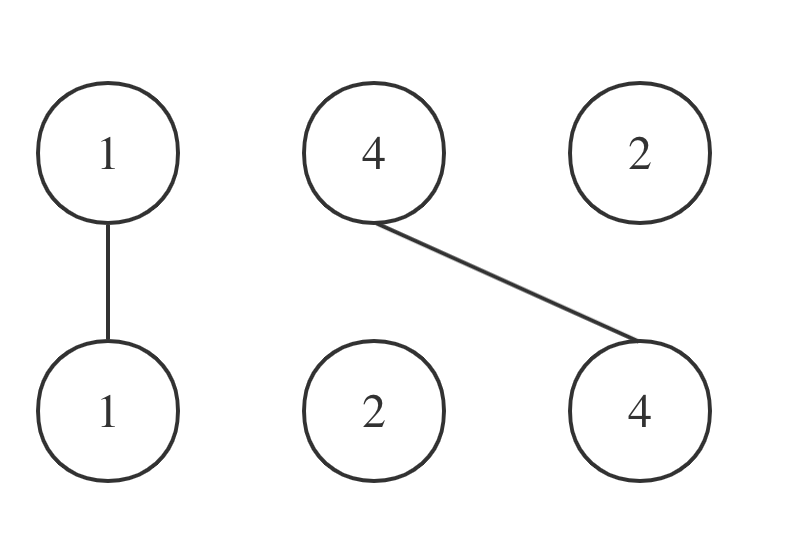
在递归的时候传引用,便可以解决,判断删除结点是父结点的左孩子还是右孩子问题。我们不需要再记录父结点。通过下面这个案例来加深理解,传引用赋值的话,10的右指针直接指向14的左孩子13,如果不传引用赋值的话,那么10的右指针保存的地址不变,还是14结点地址,而14结点被delete掉了,再次访问就会报错
相关OJ复习直达
1、二叉树的分层遍历2
2、二叉树搜索树转换成排序双向链表
3、根据二叉树的前序和中序遍历结果还原该二叉树
4、根据二叉树的中序和后序遍历结果还原该二叉树
5、二叉树的前序遍历,非递归迭代实现
6、二叉树中序遍历 ,非递归迭代实现
7、二叉树的后序遍历 ,非递归迭代实现








![[C++项目] Boost文档 站内搜索引擎(3): 建立文档及其关键字的正排 倒排索引、jieba库的安装与使用...](https://img-blog.csdnimg.cn/img_convert/fc0e861d01e0270ee1e9a3ad197899cc.png)