目录

考核方式

ACM模式

JavaScript(V8)

JavaScript(Node)

数组

折半 / 二分查找

螺旋矩阵*

前缀和-区间求和

差分数组-区间增减

滑动窗口-子串

链表

双指针（快慢指针）

有序数组的平方

删除/覆盖数组元素

最小长度的子数组

三数之和a+b+c=target

四数之和a+b+c+d=target

 二叉树

(反)序列化二叉树

前序遍历（迭代）

中序遍历（迭代）

后序遍历（迭代）

层序遍历

判断对称二叉树

判断完全二叉树

判断平衡二叉树

二叉树的镜像

最近公共祖先

数组和树

扁平结构(一维数组)转树

数组扁平化

排序

快速排序

回溯O(N!)

框架

全排列（不包含重复的数字） 

N皇后

动态规划(Dynamic Programming，DP)

斐波那契(Fibonacci）数列（递归）

数塔（递推）

最长公共子序列(LCS)

最长回文子串

最小路径和 

背包

01背包

完全背包

技巧

不用顺着题目思路来

输出为值（eg：Yes/No）

时间复杂度

数据规模

面试手撕

合法的URL

千位分割

常用方法/值

Math/Number

Map（set\delete\get\has）

Set（add/delete/has）

set判断===相等*

Array

输出arr->srting：arr.join(separator)  arr.toString()

初始化数组：new Array(length).fill(value)

增删：arr.(un)shift/pop/splice(start,delCnt,item...)

arr.includes()

array.findIndex(item => item >30);

array.find(item => item> 30);

String

输入str->arr：str.split(separator/reg)

str.substring(indexStart[, indexEnd])

str.indexOf(searchString[, position]) 

str.includes()

正则表达式Regular Expression(RegExp) 

str.match(regexp): [values]

str.search(regexp): idx

str.replace(regexp|substr, newSubStr|function)

修饰符：i大小写不敏感

边界量词：^首$尾

考前复习

考核方式

ACM模式

自己构造输入格式，控制返回格式，OJ不会给任何代码，不同的语言有不同的输入输出规范。

JavaScript(V8)

ACMcoder OJ

readline()获取单行字符串

key：

read_line()//将读取至多1024个字符，一定注意看题目字符上限
gets(n)//将读取至多n个字符，当还未达到n个时如果遇到回车或结束符

printsth(sth, ...)//多个参数时，空格分隔；最后不加回车。
console.log(sth, ...)、print(sth, ...)//多个参数时，空格分隔；最后加回车

line.split(' ').map(e=>Number(e));//str->arr
arr.push([]);//arr[]->arr[][]

//单行输入
while(line=readline()){
    //字符数组
    var lines = line.split(' ');
    //.map(Number)可以直接将字符数组变为数字数组
    var lines = line.split(' ').map(Number);  
    
    var a = parseInt(lines[0]);//效果等同下面
    var b = +lines[1];         //+能将str转换为num
    print(a+b);
}

//矩阵的输入
while (line = readline()) {
    let nums = line.split(' ');//读取第一行
    var row = +nums[0];//第一行的第一个数为行数
    var col = +nums[1];//第一行的第二个数为列数
    var map = [];//用于存放矩阵
    for (let i = 0; i < row; i++) {
        map.push([]);
        let mapline = readline().split(' ');
        for (let j = 0; j < col; j++) {
            map[i][j] = +mapline[j];
        }
    }
}

JavaScript(Node)

华为只可以采用Javascript(Node)

校招笔试真题_C++工程师、golang工程师_牛客网

模板1
var readline = require('readline')
// 创建读取行接口对象
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout
})
单行
//监听换行，接受数据
rl.on('line', function(line) {
  //line为输入的单行字符串，split函数--通过空格将该行数据转换为数组。
  var arr= line.split(' ')
  //数组arr的每一项都是字符串格式，如果我们需要整型，则需要parseInt将其转换为数字
  console.log(parseInt(arr[0]) + parseInt(arr[1]));
})

多行
const inputArr = [];//存放输入的数据
rl.on('line', function(line){
  //line是输入的每一行，为字符串格式
    inputArr.push(line.split(' '));//将输入流保存到inputArr中（注意为字符串数组）
}).on('close', function(){
    console.log(fun(inputArr))//调用函数并输出
})

//解决函数
function fun() {
	xxxxxxxx
	return xx
}
模板2
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void async function () {
    // Write your code here
    while(line = await readline()){
        let tokens = line.split(' ');
        let a = parseInt(tokens[0]);
        let b = parseInt(tokens[1]);
        console.log(a + b);
    }
}()

数组

折半 / 二分查找

判定树：描述 折半查找过程

ASLsucc≈log2(n+1)-1

keys: [L,R] while(L<=R)

螺旋矩阵*

/**
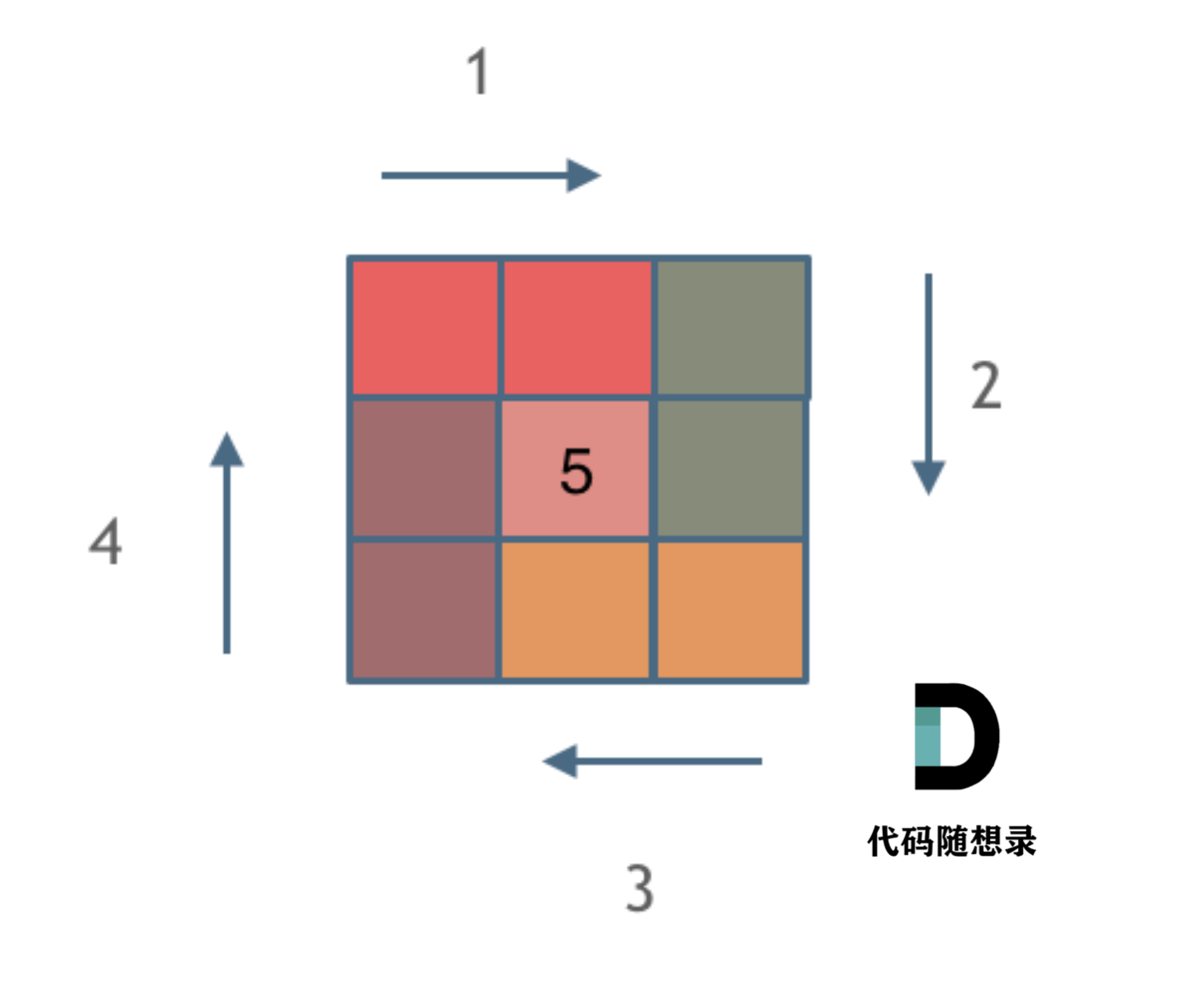
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function(n) {
    let startX = startY = 0;   // 起始位置
    let loop = Math.floor(n/2);   // 旋转圈数
    let mid = Math.floor(n/2);    // 中间位置
    let offset = 1;    // 控制每一层填充元素个数
    let count = 1;     // 更新填充数字
    let res = new Array(n).fill(0).map(() => new Array(n).fill(0));

    while (loop--) {
        let row = startX, col = startY;
        // 上行从左到右（左闭右开）
        for (; col < startY + n - offset; col++) {
            res[row][col] = count++;
        }
        // 右列从上到下（左闭右开）
        for (; row < startX + n - offset; row++) {
            res[row][col] = count++;
        }
        // 下行从右到左（左闭右开）
        for (; col > startY; col--) {
            res[row][col] = count++;
        }
        // 左列做下到上（左闭右开）
        for (; row > startX; row--) {
            res[row][col] = count++;
        }

        // 更新起始位置
        startX++;
        startY++;

        // 更新offset
        offset += 2;
    }
    // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
    if (n % 2 === 1) {
        res[mid][mid] = count;
    }
    return res;
};

前缀和-区间求和

差分数组-区间增减

滑动窗口-子串

int left = 0, right = 0;

while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    right++;

    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

链表

虚拟头结点

 let ret = new ListNode(0, head), temp = ret;

双指针（快慢指针）

有序数组的平方

删除/覆盖数组元素

if(nums[i] != val){
            nums[k++] = nums[i]
        }

最小长度的子数组

let ans = Infinity
    
    while(end < len){
        sum += nums[end];
        while (sum >= target) {
            ans = Math.min(ans, end - start + 1);
            sum -= nums[start];
            start++;
        }
        end++;
    }

三数之和a+b+c=target

arr.sort()

 let l = i + 1, r = len - 1, iNum = nums[i]
        // 数组排过序，如果第一个数大于0直接返回res
        if (iNum > 0) return res
        // 去重
        if (iNum == nums[i - 1]) continue

res.push([iNum, lNum, rNum])
                // 去重
                while(l < r && nums[l] == nums[l + 1]){
                    l++
                }
                while(l < r && nums[r] == nums[r - 1]) {
                    r--
                }
                l++
                r--

四数之和a+b+c+d=target

    for(let i = 0; i < len - 3; i++) {
        // 去重i
        if(i > 0 && nums[i] === nums[i - 1]) continue;

 二叉树

(反)序列化二叉树

序列化二叉树，key：

•     let arr = Array.isArray(s) ? s : s.split("");
•     let a = arr.shift();
•     let node = null;
•     if (typeof a === "number")

function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
}
//反序列化二叉树：tree->str 把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串
function Serialize(pRoot, arr = []) {
    if (!pRoot) {
        arr.push("#");
        return arr;
    } else {
        arr.push(pRoot.val);//注意是val。而不是root
        Serialize(pRoot.left, arr);
        Serialize(pRoot.right, arr);
    }
    return arr;
}
//序列化二叉树：str->tree 根据字符串结果str，重构二叉树
function Deserialize(s) {
    //转换为数组
    let arr = Array.isArray(s) ? s : s.split("");
    //取出val
    let a = arr.shift();
    //构建二叉树结点
    let node = null;
    if (typeof a === "number") {
        //还有可能等于#
        node = new TreeNode(a);
        node.left = Deserialize(arr);
        node.right = Deserialize(arr);
    }
    return node;
}
module.exports = {
    Serialize: Serialize,
    Deserialize: Deserialize,
};

前序遍历（迭代）

入栈：中右左

出栈：中左右

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function(root) {
    let stack=[]
    let res = []
    let cur = null;
    if(!root) return res;
    root&&stack.push(root)
    while(stack.length){
        cur = stack.pop()
        res.push(cur.val)
        cur.right&&stack.push(cur.right)
        cur.left&&stack.push(cur.left)
    }
    return res
};

中序遍历（迭代）

指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    let stack = []
    let res = []
    let cur = root
    while(cur||stack.length){
        if(cur){
            stack.push(cur)
            cur = cur.left
        } else {
            cur = stack.pop()
            res.push(cur.val)
            cur = cur.right
        }
    }
    return res
};

后序遍历（迭代）

和前序遍历不同：

入栈：中左右

出栈：中右左

rever出栈：左右中

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function(root) {
    let stack = []
    let res = []
    let cur = root
    if(!root) return res
    stack.push(root)
    while(stack.length){
        cur = stack.pop()
        res.push(cur.val)
        cur.left&&stack.push(cur.left)
        cur.right&&stack.push(cur.right)
    }
    return res.reverse()

};

层序遍历

树的层序遍历，相似 图的广度优先搜索

1. 初始设置一个空队，根结点入队
2. 队首结点出队，其左右孩子 依次 入队
3. 若队空，说明 所有结点 已处理完，结束遍历；否则（2)

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */

/**
 *
 * @param root TreeNode类
 * @return int整型二维数组
 */
function levelOrder(root) {
    // write code here
    if (root == null) {
        return [];
    }

    const arr = [];
    const queue = [];

    queue.push(root);

    while (queue.length) {
        const preSize = queue.length;
        const floor = [];//当前层
        for (let i = 0; i < preSize; ++i) {
            const v = queue.shift();
            floor.push(v.val);
            v.left&&queue.push(v.left);
            v.right&&queue.push(v.right);
        }
        arr.push(floor);
    }
    return arr;//[[1],[2,3]]
}
module.exports = {
    levelOrder: levelOrder,
};

判断对称二叉树

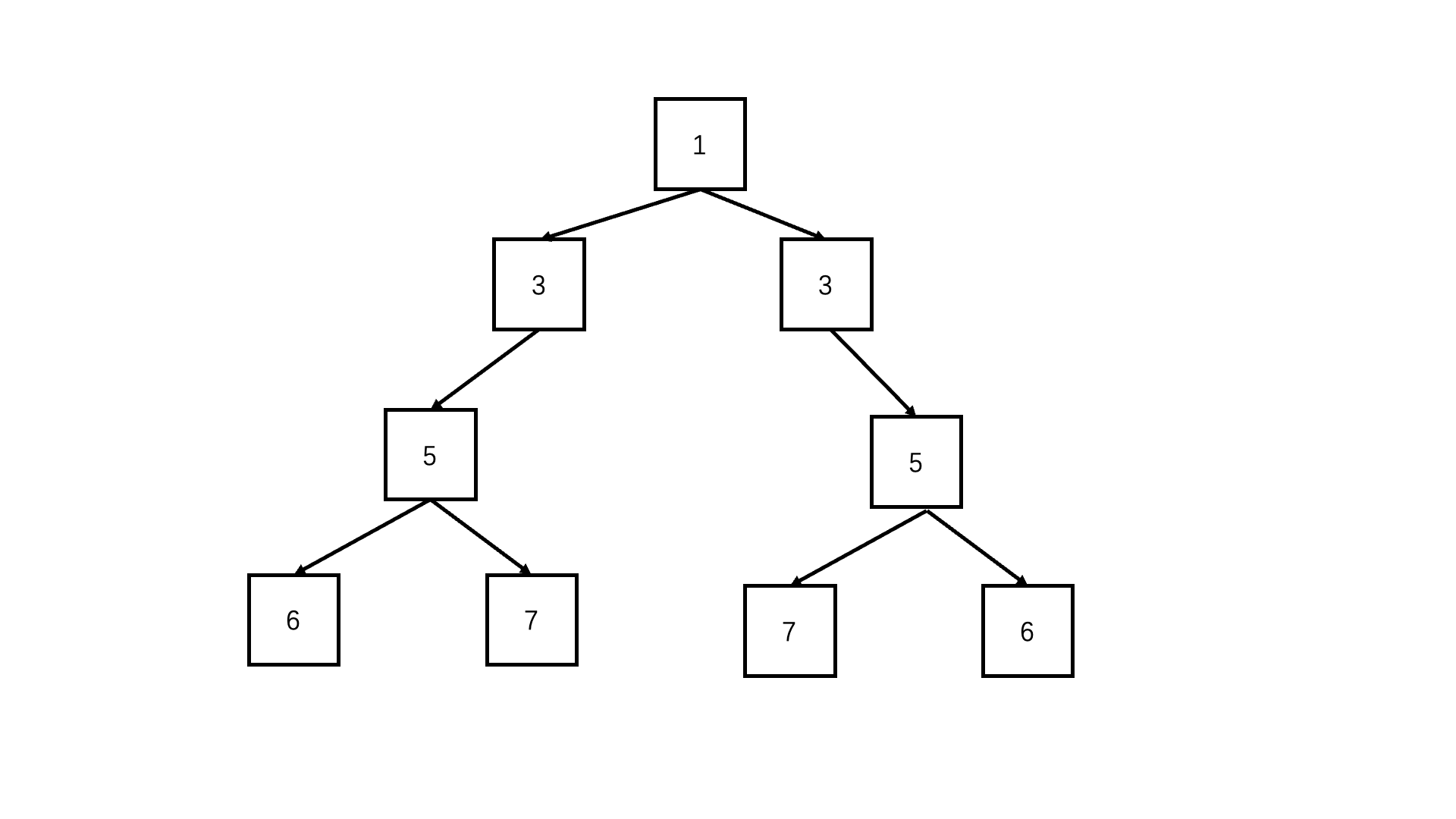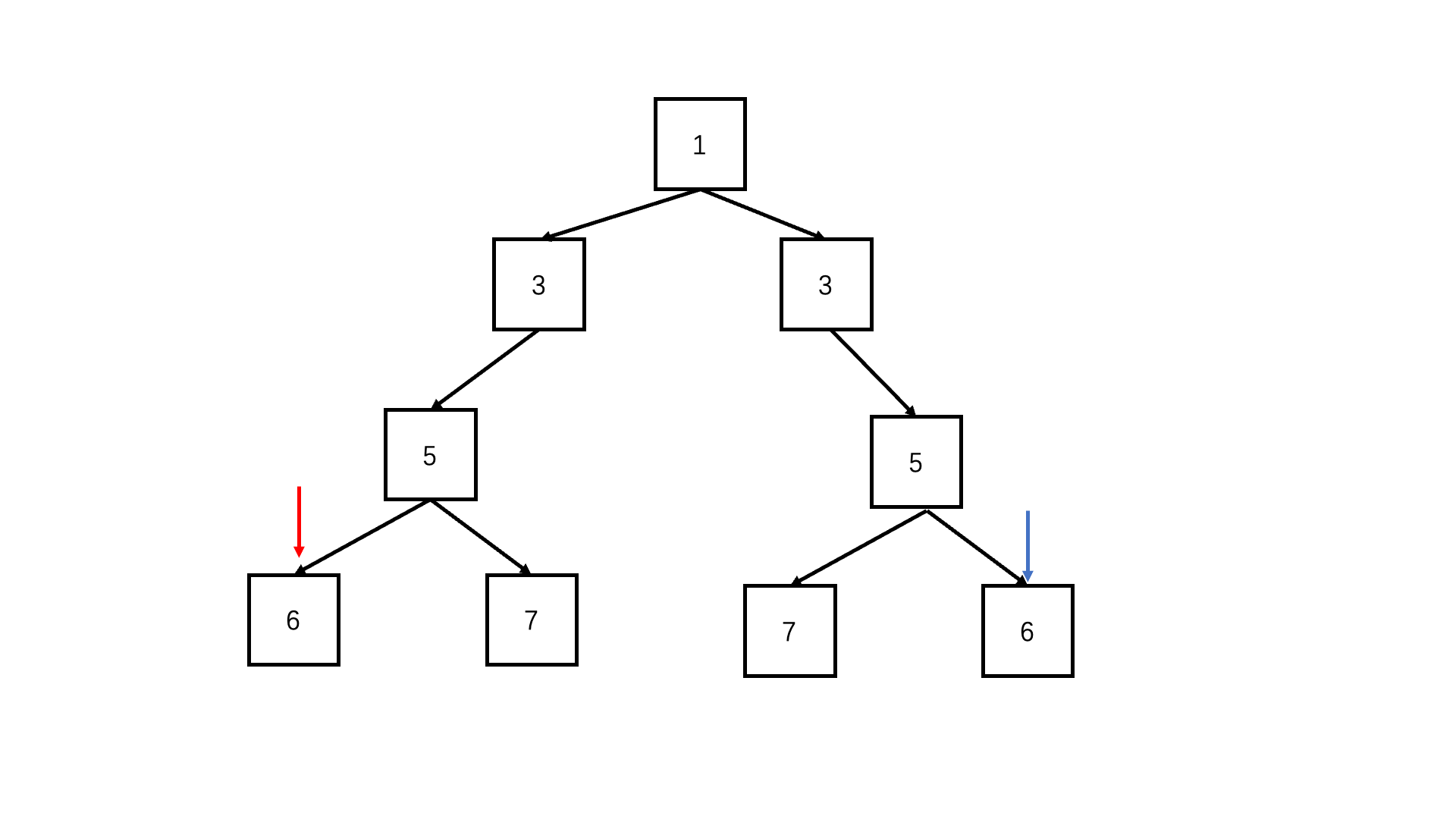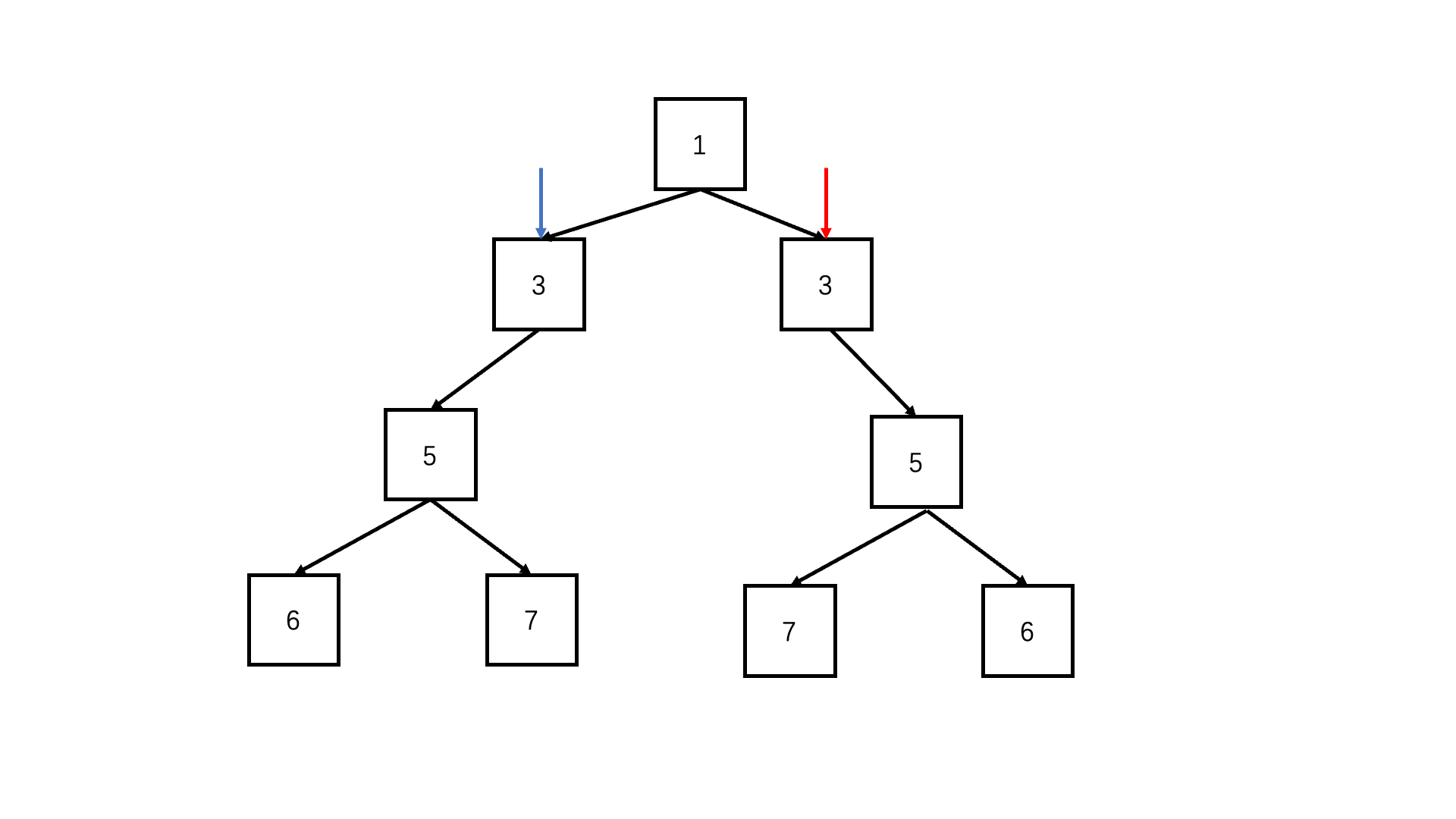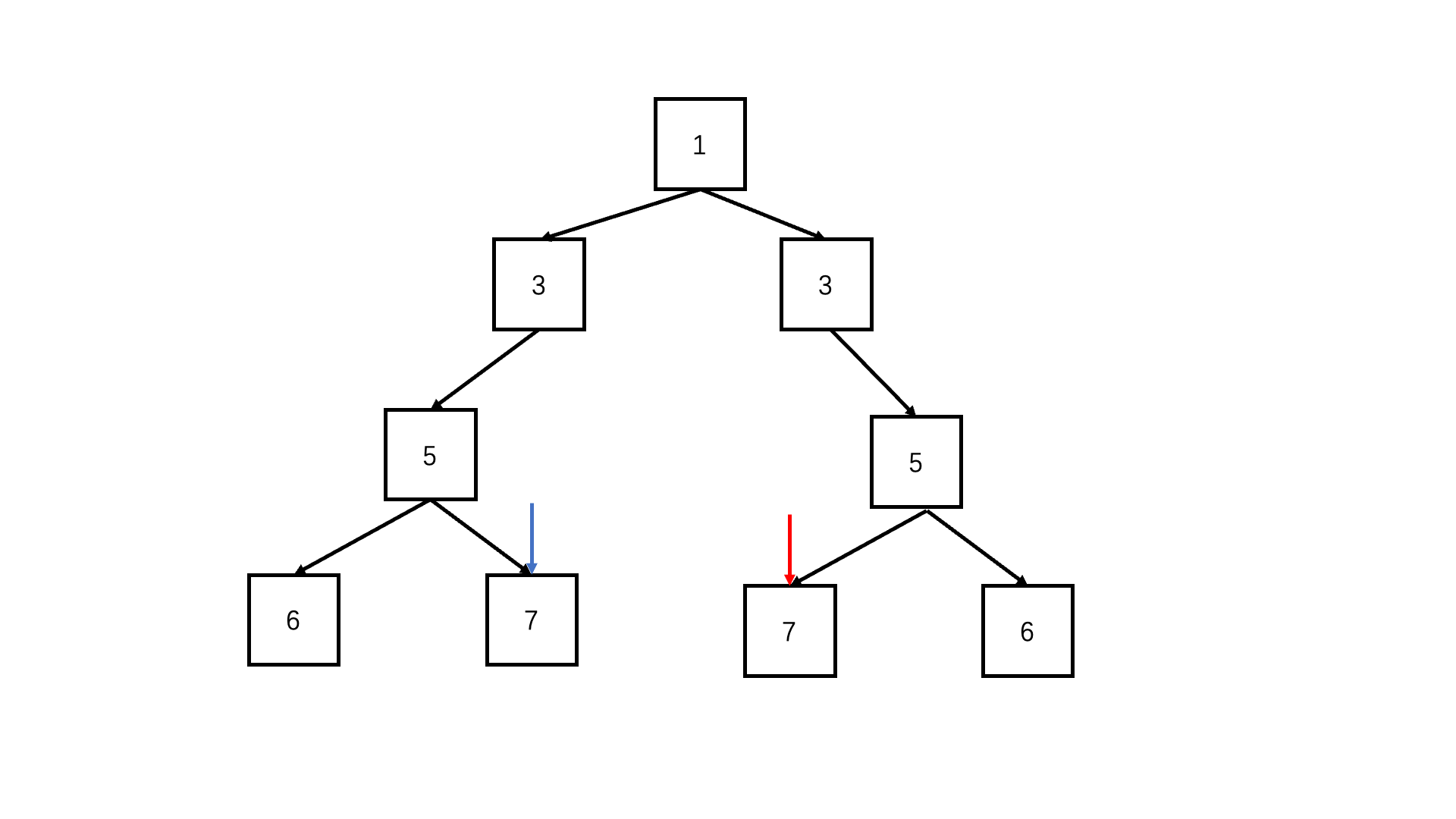
/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
let flag = true;
function deep(left, right) {
    if (!left && !right) return true; //可以两个都为空
    if (!right||!left|| left.val !== right.val) {//只有一个为空或者节点值不同，必定不对称
        return false;
    }
    return deep(left.left, right.right) && deep(left.right, right.left); //每层对应的节点进入递归比较
}
function isSymmetrical(pRoot) {
    return deep(pRoot, pRoot);
}
module.exports = {
    isSymmetrical: isSymmetrical,
};

判断完全二叉树

完全二叉树：叶子节点只能出现在最下层和次下层，且最下层的叶子节点集中在树的左部。

/*
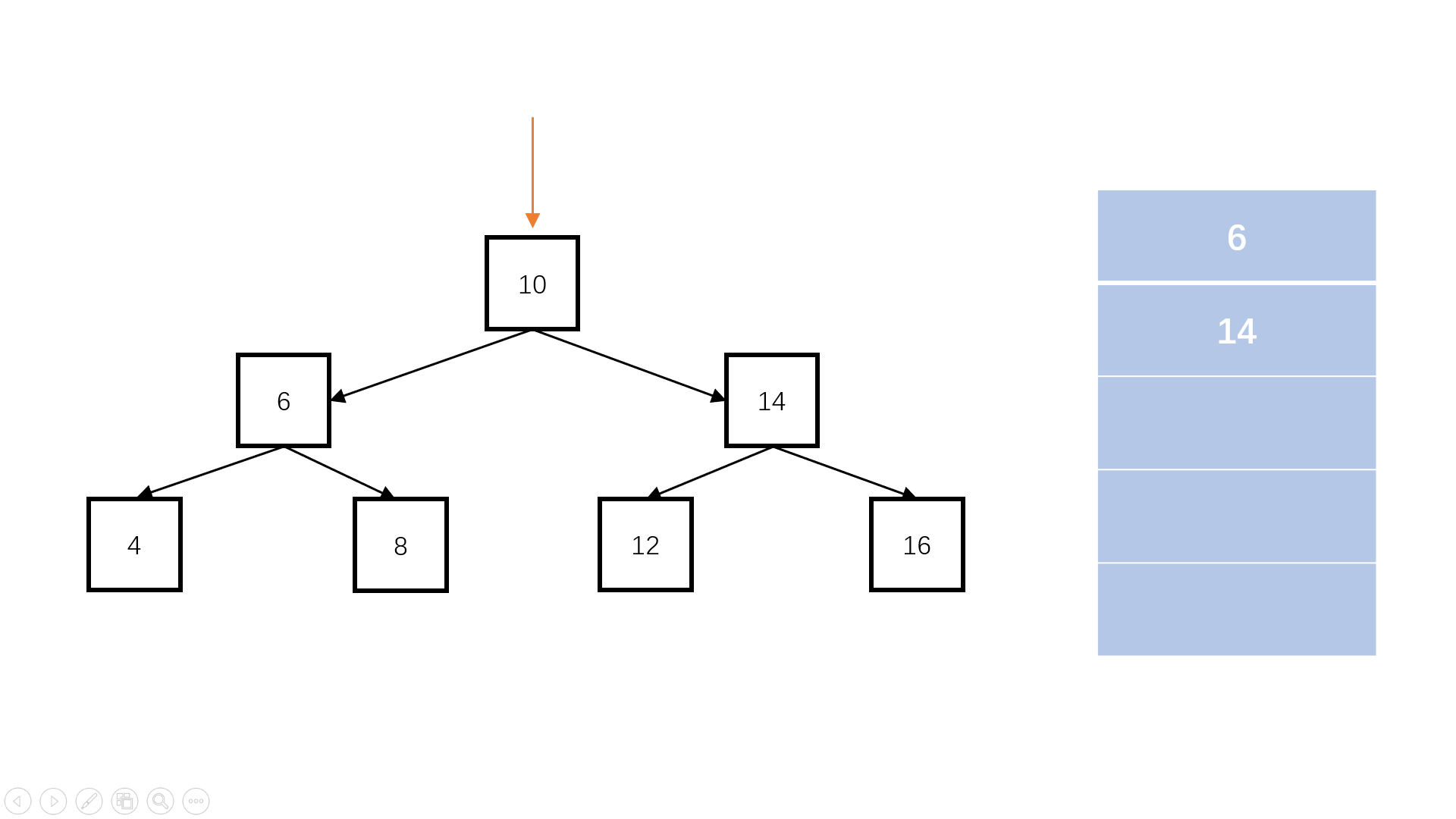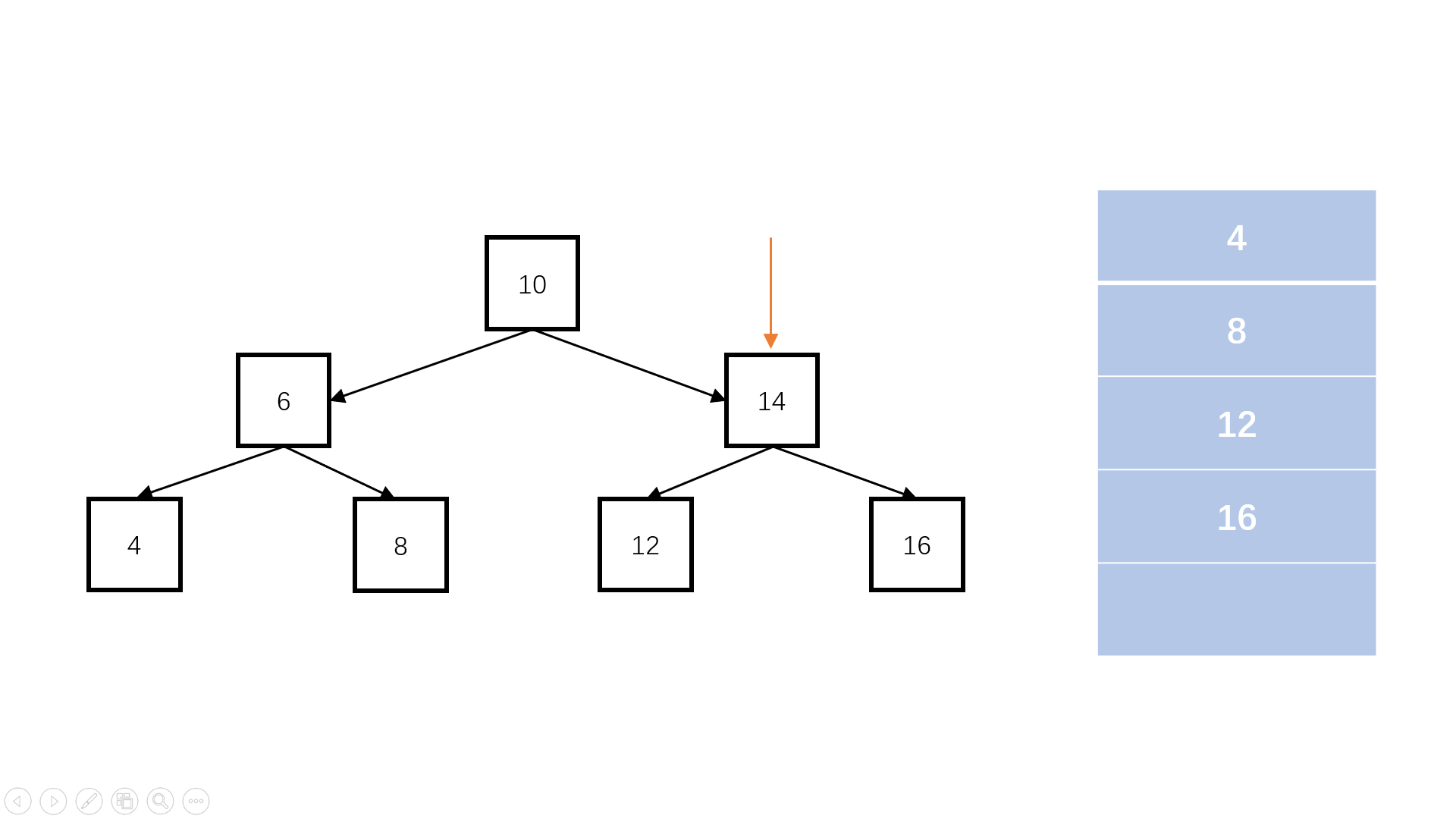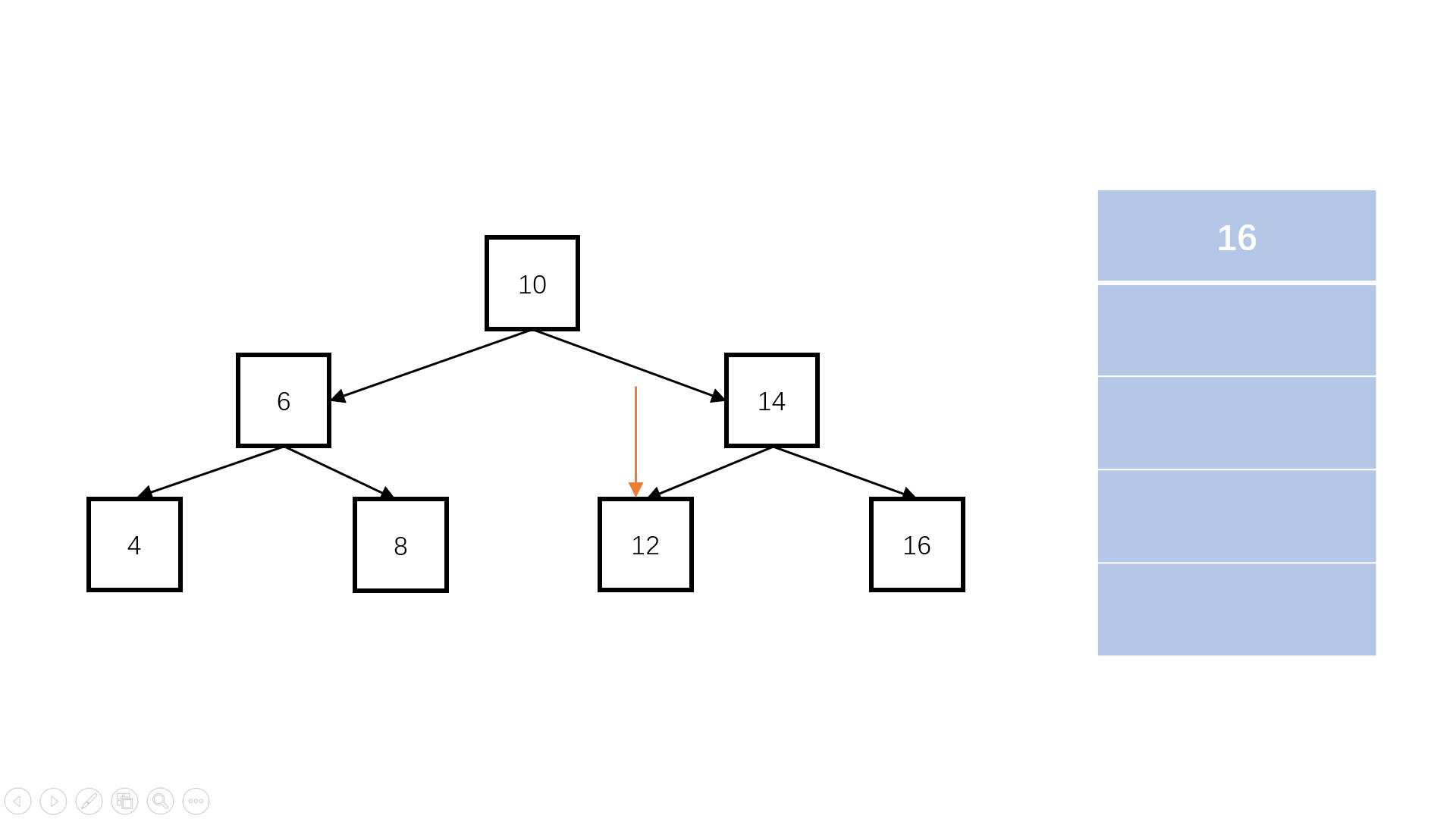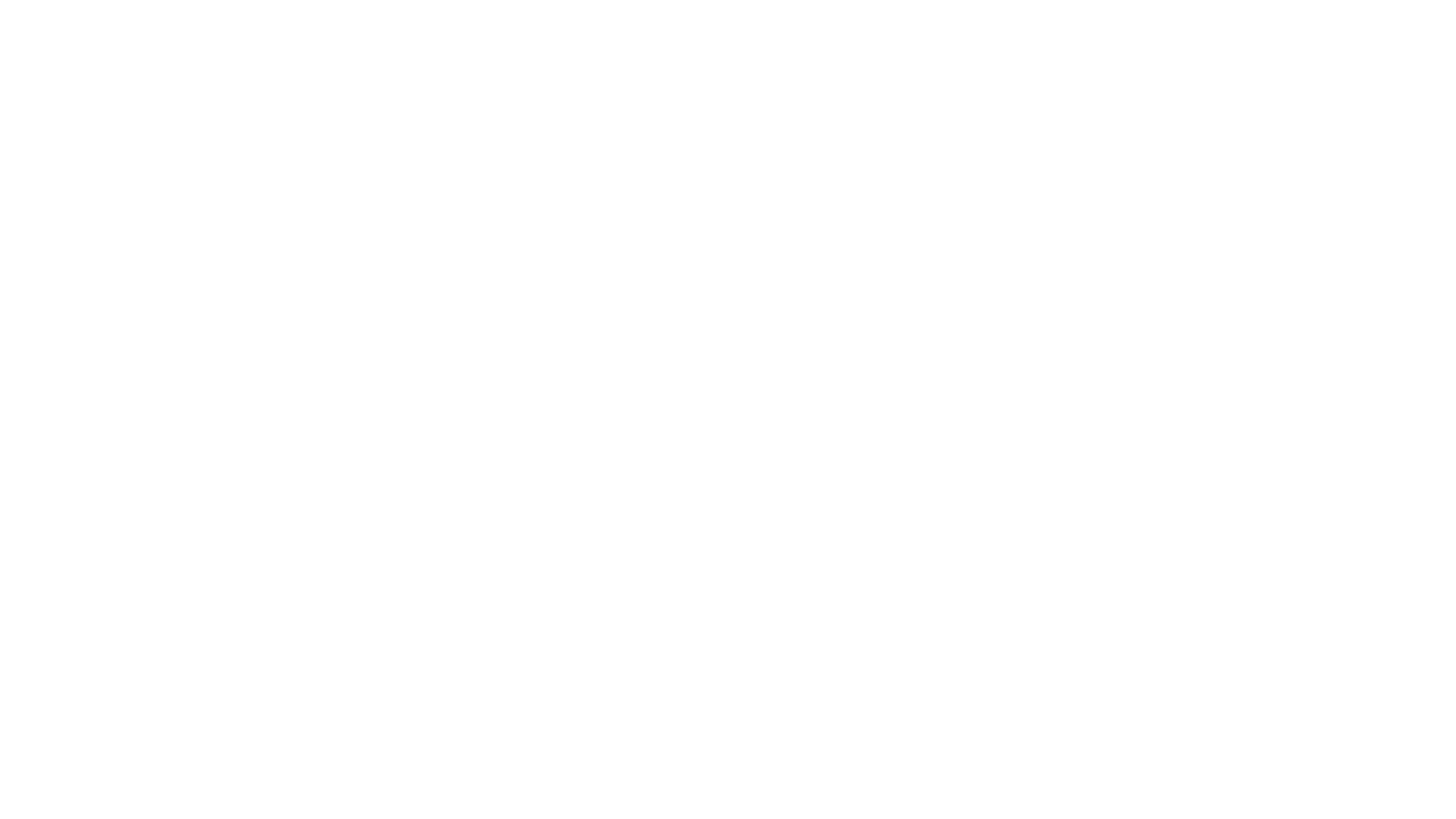
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 *
 * @param root TreeNode类
 * @return bool布尔型
 */
function isCompleteTree(root) {
    // write code here
    if (root == null) return true;

    const queue = [];
    queue.push(root);

    let flag = false; //是否遇到空节点
    while (queue.length) {
        const node = queue.shift();
        if (node == null) {
            //如果遇到某个节点为空，进行标记，代表到了完全二叉树的最下层
            flag = true;
            continue;
        }

        if (flag == true) {
            //若是后续还有访问，则说明提前出现了叶子节点，不符合完全二叉树的性质。
            return false;
        }

        queue.push(node.left);
        queue.push(node.right);
    }
    return true;
}
module.exports = {
    isCompleteTree: isCompleteTree,
};

判断平衡二叉树

平衡二叉树是左子树的高度与右子树的高度差的绝对值小于等于1，同样左子树是平衡二叉树，右子树为平衡二叉树。

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
function IsBalanced_Solution(pRoot)
{
    if(!pRoot) return true;
    // write code here
    return (Math.abs(getMaxDepth(pRoot.left) - getMaxDepth(pRoot.right)) <=1) && IsBalanced_Solution(pRoot.left) && IsBalanced_Solution(pRoot.right)
}

function getMaxDepth(root) {
    if(!root) return 0;
    return Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
}
module.exports = {
    IsBalanced_Solution : IsBalanced_Solution
};

二叉树的镜像

先序遍历

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param pRoot TreeNode类 
 * @return TreeNode类
 */
function Mirror( pRoot ) {
    
    function traversal(root){
        if(root===null) return ;
        //交换左右孩子
        let temp = root.left;
        root.left = root.right;
        root.right = temp;

        traversal(root.left);
        traversal(root.right);
        return root;
    }
    
    return traversal(pRoot);
    // write code here
}
module.exports = {
    Mirror : Mirror
};

最近公共祖先

如果从两个节点往上找，每个节点都往上走，一直走到根节点，那么根节点到这两个节点的连线肯定有相交的地方，

如果从上往下走，那么最后一次相交的节点就是他们的最近公共祖先节点。

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */

/**
 *
 * @param root TreeNode类
 * @param o1 int整型
 * @param o2 int整型
 * @return int整型
 */
function dfs(root, o1, o2) {
    if (root == null || root.val == o1 || root.val == o2) {
        return root;
    }
    //递归遍历左子树
    let left = dfs(root.left, o1, o2);
    //递归遍历右子树
    let right = dfs(root.right, o1, o2);
    //如果left、right都不为空，那么代表o1、o2在root的两侧，所以root为他们的公共祖先
    if (left && right) return root;
    //如果left、right有一个为空，那么就返回不为空的那一个
    return left != null ? left : right;
}

数组和树

扁平结构(一维数组)转树

key：

1. pid：parent id 
2. obj[item.id] = { ...item, children: [] }
3. pid === 0
4. !obj[pid]
5. obj[pid].children.push(treeitem)

   //pid：parent id 
   let arr = [
        { id: 1, name: '部门1', pid: 0 },
        { id: 2, name: '部门2', pid: 1 },
        { id: 3, name: '部门3', pid: 1 },
        { id: 4, name: '部门4', pid: 3 },
        { id: 5, name: '部门5', pid: 4 },
    ]

    // // 上面的数据转换为 下面的 tree 数据
    // [
    //     {
    //         "id": 1,
    //         "name": "部门1",
    //         "pid": 0,
    //         "children": [
    //             {
    //                 "id": 2,
    //                 "name": "部门2",
    //                 "pid": 1,
    //                 "children": []
    //             },
    //             {
    //                 "id": 3,
    //                 "name": "部门3",
    //                 "pid": 1,
    //                 "children": [
    //                     {
    //                         id: 4,
    //                         name: '部门4',
    //                         pid: 3,
    //                         "children": [
    //                             {
    //                                 id: 5,
    //                                 name: '部门5',
    //                                 pid: 4,
    //                                 "children": []
    //                             },
    //                         ]
    //                     },
    //                 ]
    //             }
    //         ]
    //     }
    // ]


    function tree(items) {
        // 1、声明一个数组和一个对象 用来存储数据
        let arr = []
        let obj = {}
        // 2、给每条item添加children ，并连带一起放在obj对象里
        for (let item of items) {
            obj[item.id] = { ...item, children: [] }
        }
        // 3、for of 逻辑处理
        for (let item of items) {
            // 4、把数据里面的id 取出来赋值 方便下一步的操作
            let id = item.id
            let pid = item.pid
            // 5、根据 id  将 obj 里面的每一项数据取出来
            let treeitem = obj[id]
            // 6、如果是第一项的话 吧treeitem 放到 arr 数组当中
            if (pid === 0) {
                // 把数据放到 arr 数组里面
                arr.push(treeitem)
            } else {
                // 如果没有 pid 找不到 就开一个 obj { }
                if (!obj[pid]) {
                    obj = {
                        children: []
                    }
                }

                // 否则给它的 obj 根基 pid（自己定义的下标） 进行查找 它里面的children属性 然后push
                obj[pid].children.push(treeitem)
            }
        }
        // 返回处理好的数据
        return arr
    }
    console.log(tree(arr))

数组扁平化

要求将数组参数中的多维数组扩展为一维数组并返回该数组。
数组参数中仅包含数组类型和数字类型

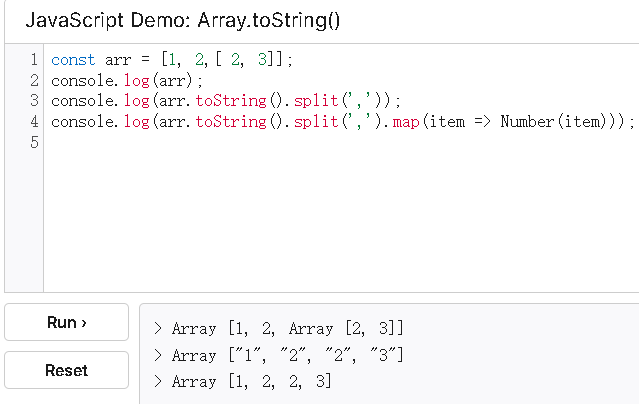
function flatten(arr){
    // toString() + split() 实现   
    return arr.toString().split(',').map(item => Number(item));

    //join() + split() 实现
    return arr.join(',').split(',').map(item => Number(item));

    //reduce 实现
    return arr.reduce((target, item) => {
        return target.concat(Array.isArray(item) ? flatten(item) : item);
    }, [])

    // 递归实现
    let res = [];
    arr.forEach(item => {
        if (Array.isArray(item)) {
            res = res.concat(flatten(item))
      } else {
             res.push(item);
         }
     });
     return res;

    // 扩展运算符实现
       while(arr.some(item => Array.isArray(item))){
         arr = [].concat(...arr);
     }
     return arr;

    // flat()实现（这里不支持使用）
    return arr.flat(Infinity);
}

排序

快速排序

快速排序的基本思想是通过分治来使一部分均比另一部分小（大）再使两部分重复该步骤而实现有序的排列。核心步骤有：

1. 选择一个基准值（pivot）
2. 以基准值将数组分割为两部分
3. 递归分割之后的数组直到数组为空或只有一个元素为止

key：

1. pivot = array.splice(pivotIndex, 1)[0]
2.  _quickSort(left).concat([pivot], _quickSort(right))

const _quickSort = array => {
    if(array.length <= 1) return array
    var pivotIndex = Math.floor(array.length / 2)
    var pivot = array.splice(pivotIndex, 1)[0]
    var left = []
    var right = []
    for (var i=0 ; i<array.length ; i++){
        if (array[i] < pivot) {
            left.push(array[i])
        } else {
            right.push(array[i])
        }
    }
    return _quickSort(left).concat([pivot], _quickSort(right))
}

回溯O(N!)

如果不能成功，那么返回的时候我们就还要把这个位置还原。这就是回溯算法，也是试探算法。

解决一个回溯问题，实际上就是一个决策树的遍历过程。

1、路径：已选择。

2、选择列表：可选择。

3、结束条件：无选择。

框架

result = []
function backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

全排列（不包含重复的数字） 

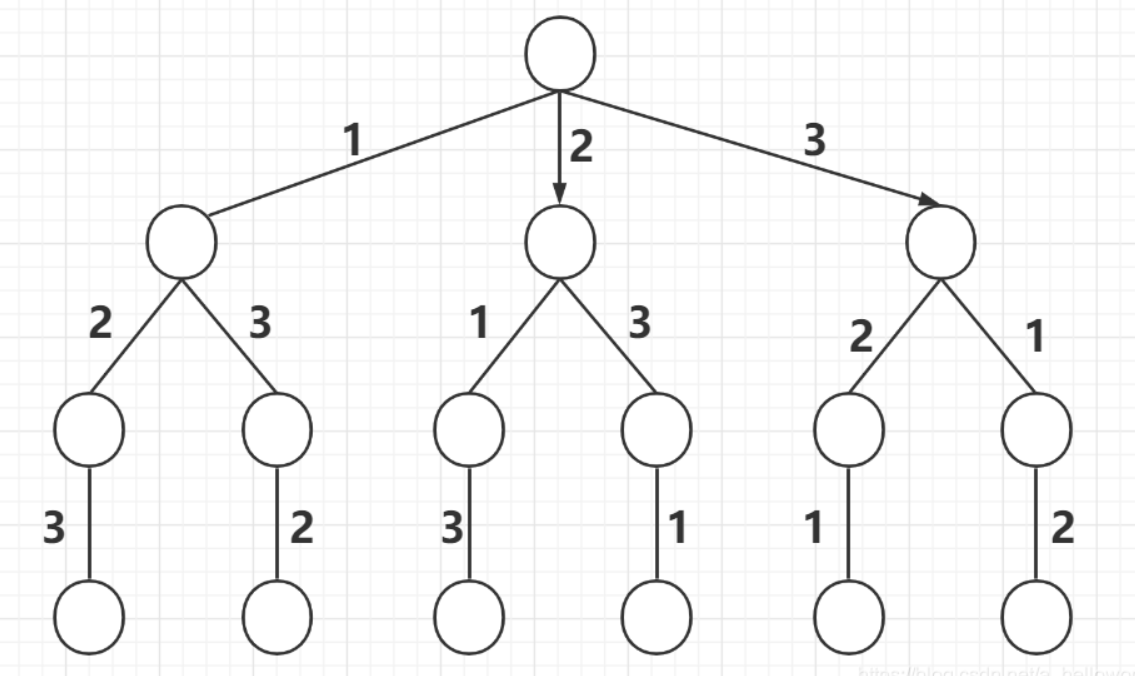
key：

1. path.length == string.length
2. path.includes(item)

const _permute = string => {
    const res = [];

    const backtrace = path => {
        if(path.length == string.length){
            res.push(path);
            return;
        }
        for(const item of string) {
            if(path.includes(item)) continue;
            backtrace(path + item);
        }
    };

    backtrace('');
    return res;
}

N皇后

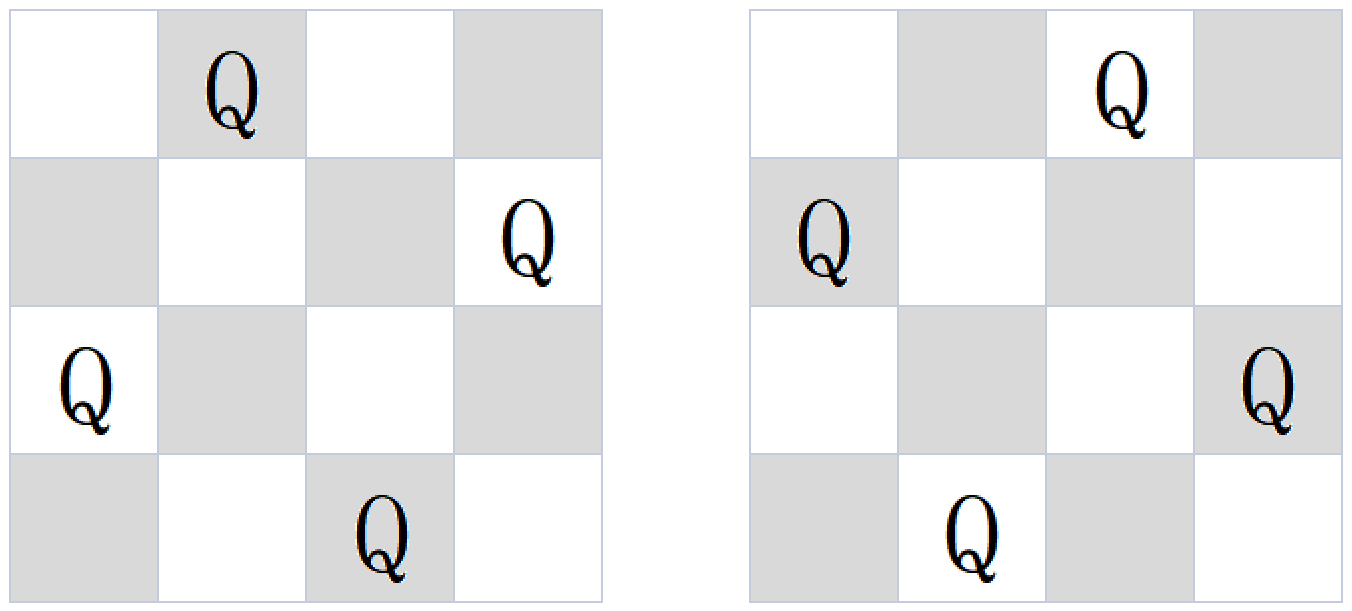
在 n * n 的棋盘上要摆 n 个皇后，
要求：任何两个皇后不同行，不同列也不在同一条斜线上，
求给一个整数 n ，返回 n 皇后的摆法数。

要求：空间复杂度 O(1) ，时间复杂度O(n!)

1. 要确定皇后的位置，其实就是确定列的位置，因为行已经固定了
2. 进一步讲，也就是如何摆放 数组arr [0,1,2,3,...,n-1]
3. 如果没有【不在同一条斜线上】要求，这题其实只是单纯的全排列问题
4. 在全排列的基础上，根据N皇后的问题，去除一些结果

• arr ：n个皇后的列位置

• res ：n皇后排列结果

• ruler： 记录对应的列位置是否已经占用（也是是否有皇后），如果有，那么设为1，没有设为0

• setPos ：哈希集合，标记正斜线（从左上到右下）位置，如果在相同正斜线上，坐标(x,y)满足 y-x 都相同，(y1 - x1)应该等于(y2 - x2)。

• setCon ：哈希集合，标记反正斜线（从y右上到左下）位置，如果在相同反斜线上，坐标(x,y)满足 x+y 都相同，(x1 + y1)应该等于(x2 + y2)。

• 是否在同一斜线上，其实就是这两个点的所形成的斜线的斜率是否为±1。点P(a,b) ，点Q(c,d)

  （1）斜率为1 (d-b)/(c-a) = 1，横纵坐标之差相等

  （2）斜率为-1 (d-b)/(c-a) = -1 ，等式两边恒等变形 a+b = c + d ，横纵坐标之和相等

/**
 *
 * @param n int整型 the n
 * @return int整型
 */
function Nqueen(n) {
    let res = []; //二维数组，存放每行Q的列坐标
    let isQ = new Array(n).fill(0); //记录该列是否有Q
    let setPos = new Set(); //标记正对角线
    let setCon = new Set(); // 标记反对角线
    //给当前row找一个col
    const backTrace = (row, path) => {
        if (path.length === n) {
            res.push(path);
            return;
        }
        for (let col = 0; col < n; col++) {
            if (
                isQ[col] == 0 &&
                !setPos.has(row - col) &&
                !setCon.has(row + col)
            ) {
                path.push(col);
                isQ[col] = 1;
                setPos.add(row - col);
                setCon.add(row + col);
                backTrace(row + 1, path);
                path.pop();
                isQ[col] = 0;
                setPos.delete(row - col);
                setCon.delete(row + col);
            }
        }
    };
    backTrace(0, []);
    return res.length;
}
module.exports = {
    Nqueen: Nqueen,
};

动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质，可以用 dp table 或者备忘录优化，将递归树大幅剪枝，这就变成了动态规划。

动态规划(Dynamic Programming，DP)

分解为简单的子问题

递归或者递推的写法来实现动态规划，其中递归写法在此处又称作记忆化搜索。

斐波那契(Fibonacci）数列（递归）

function F(n){
if(n= 0||n== 1) return 1;
else return F(n-1)+F(n-2);
}

dp[n]=-1表示F(n)当前还没有被计算过

function F(n) {
if(n == 0||n==1) return 1;//递归边界
if(dp[n] != -1) return dp[n]; //已经计算过，直接返回结果，不再重复计算else {
else dp[n] = F(n-1) + F(n-2); //计算F(n)，并保存至dp[n]
return dp [n];//返回F(n)的结果
}

数塔（递推）

第i层有i个数字。现在要从第一层走到第n层，最后将路径上所有数字相加后得到的和最大是多少?

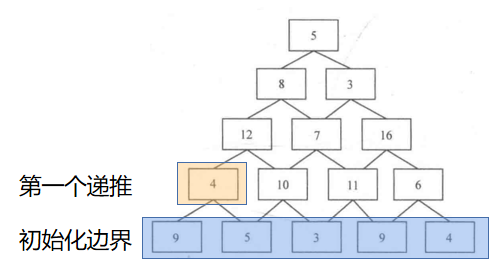
dp[i][j]表示从第i行第j个数字出发到达最底层的所有路径中能得到的最大和

dp[i][i]=max(dp[i-1][j],dp[i-1][j+1])+f[i][j]

最长公共子序列(LCS)

Longest Common Subsequence：子序列可以不连续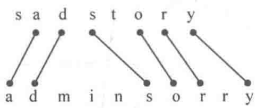
“sadstory”与“adminsorry”最长公共子序列为“adsory”

dp[i][j]：strA[i]和strB[j]之前的LCS 长度，下标从1开始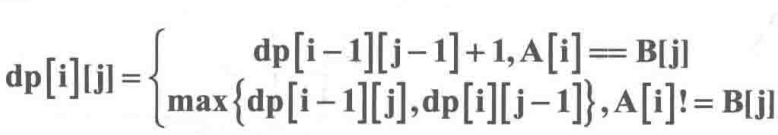

最长回文子串

dp[i][j]表示S[i]至S[j]所表示的子串是否是回文子串，是则为1，不是为0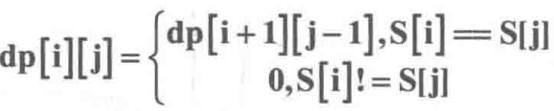

最小路径和 

mxn矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

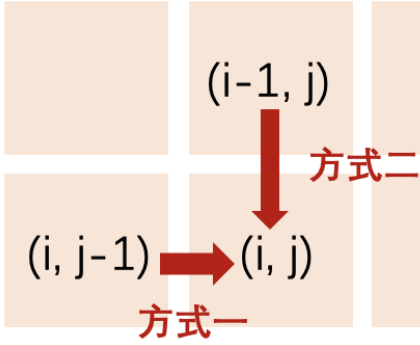dp[i][j]代表i到j的最短路径

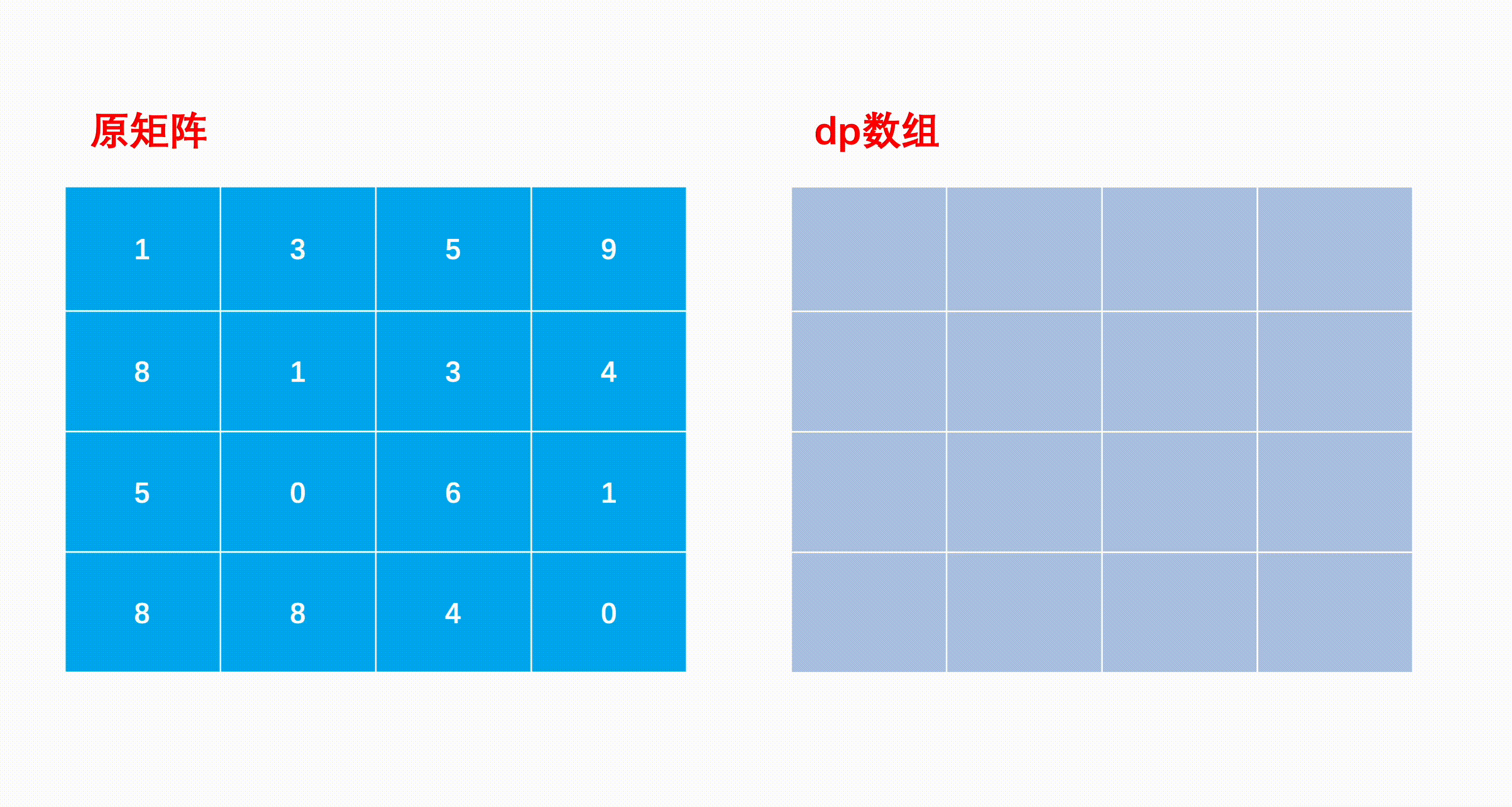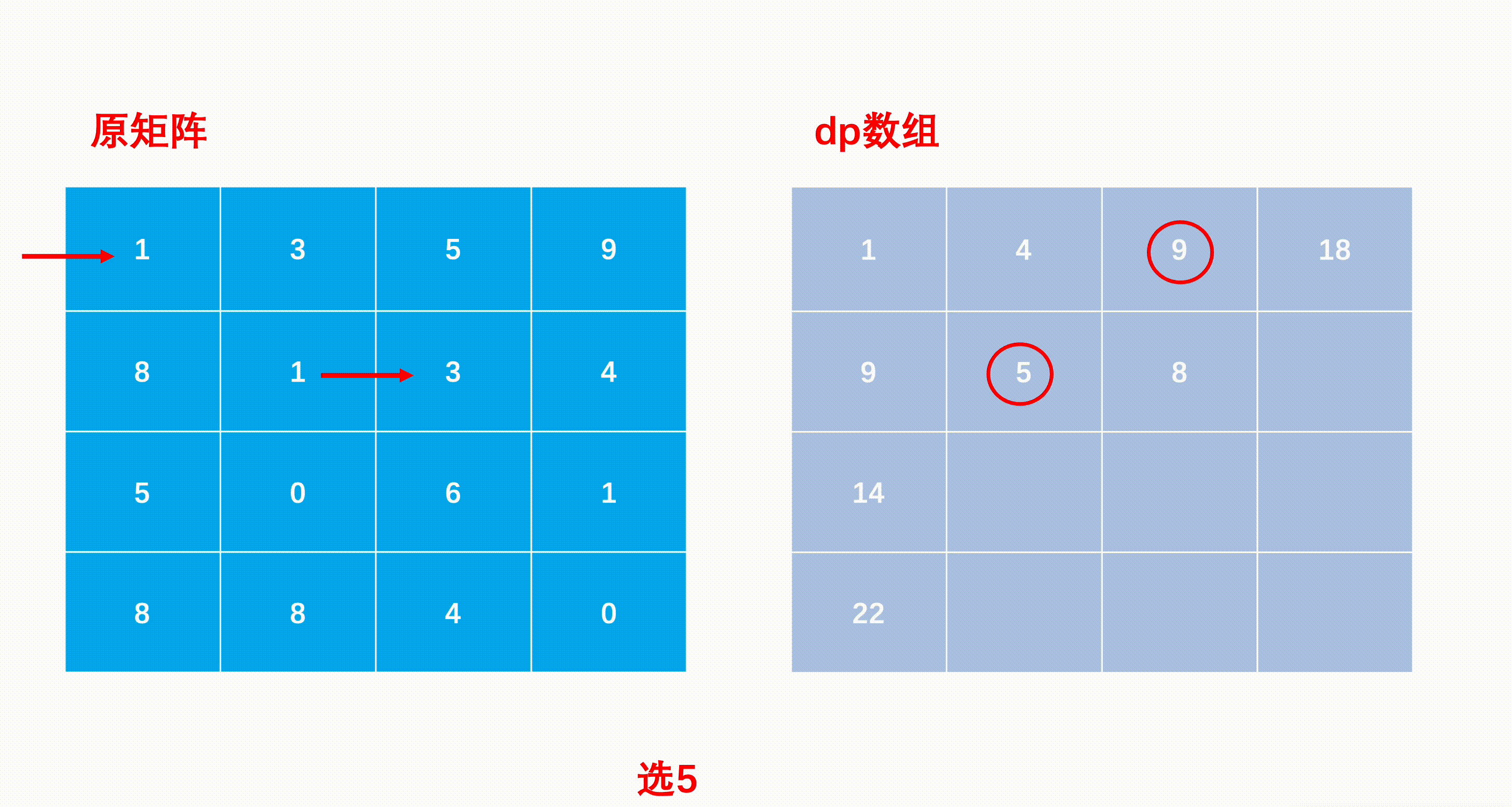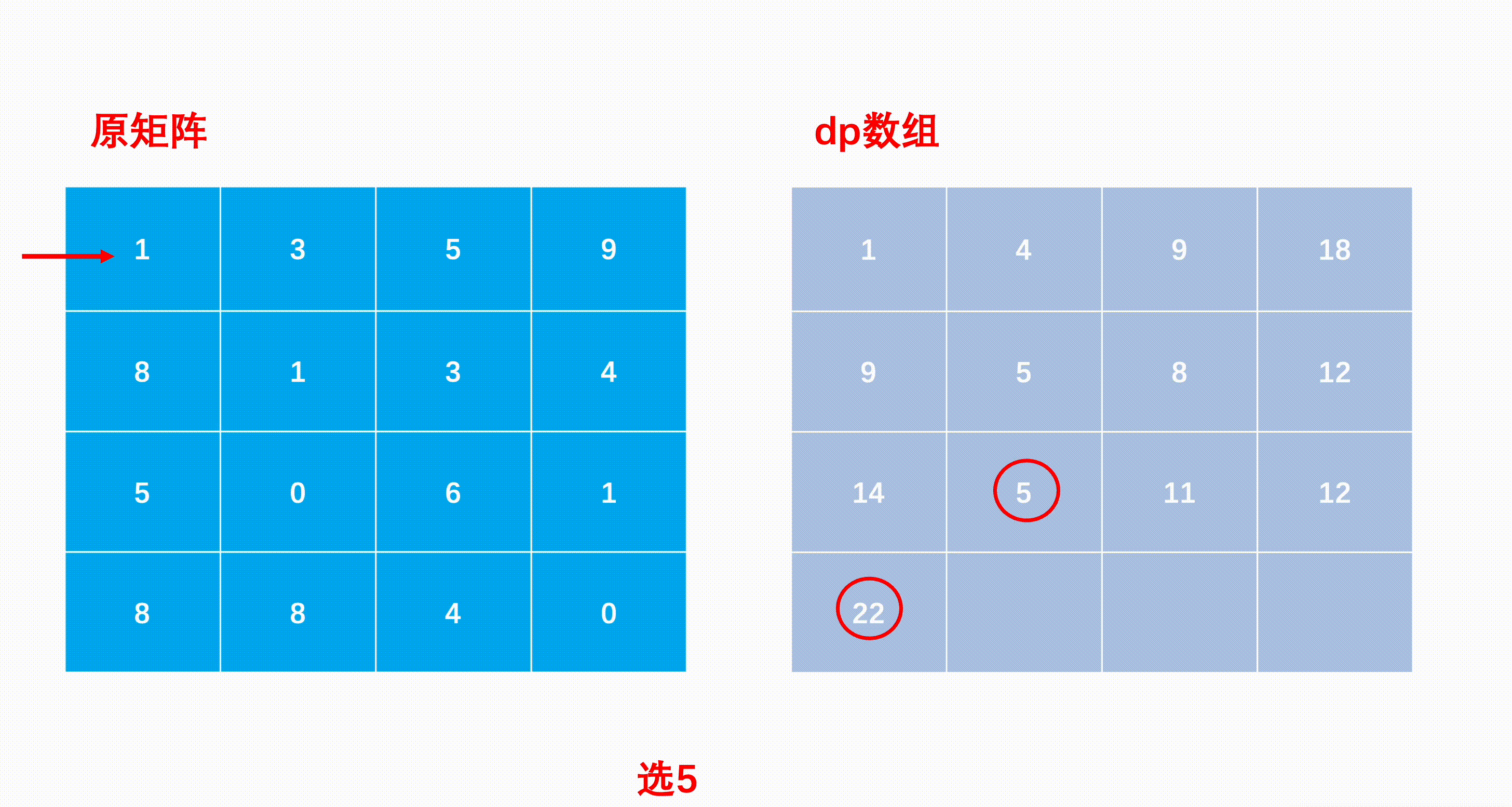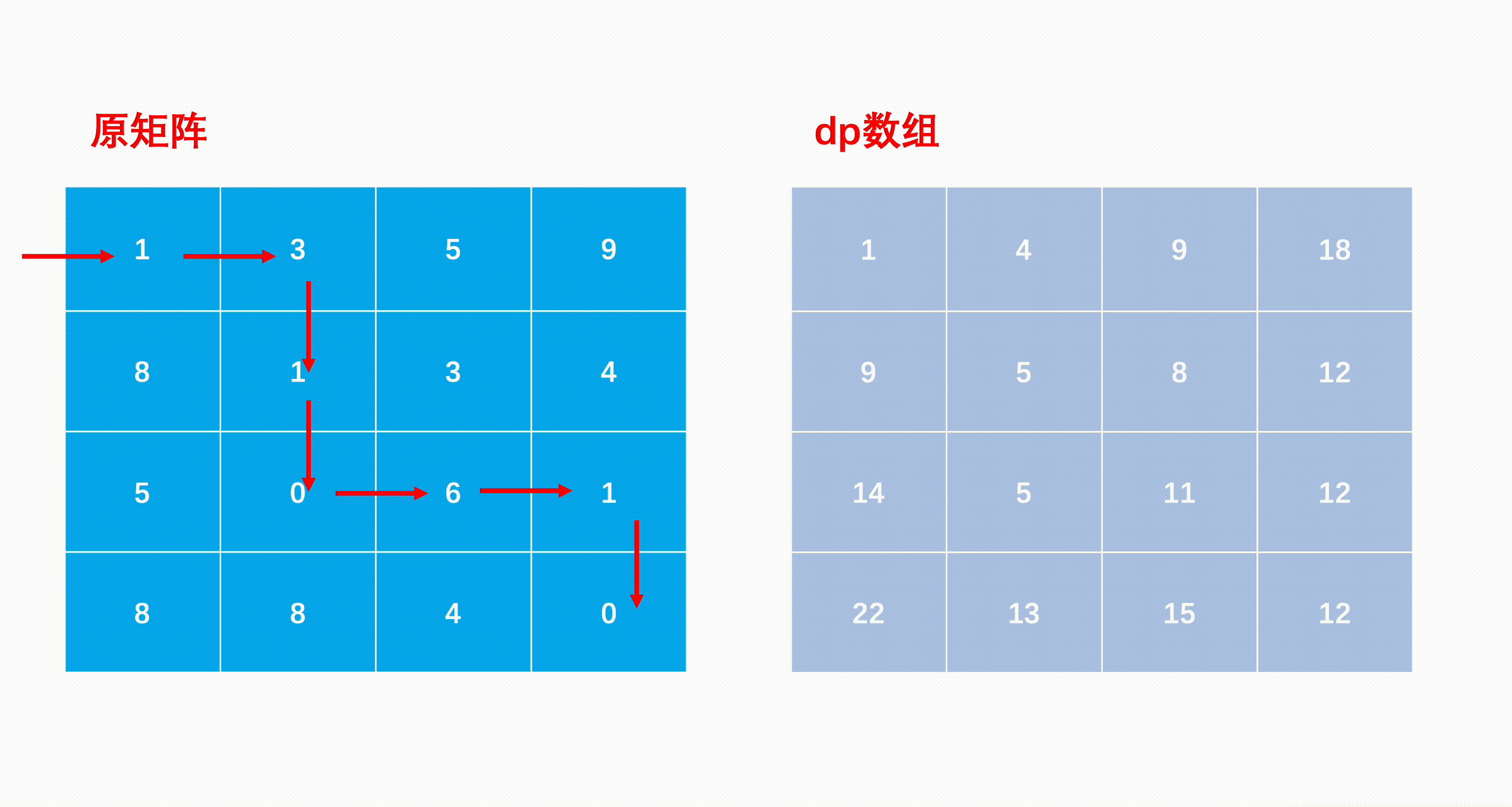
求解子问题时的状态转移方程：从「上一状态」到「下一状态」的递推式。

dp[i, j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j]

JavaScript中没有二维数组的概念，但是可以设置  数组元素的值 等于 数组

key：

1. dp[0][i] = dp[0][i - 1] + matrix[0][i];
2. dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];

function minPathSum(matrix) {
    var row = matrix.length,
        col = matrix[0].length;
    var dp = new Array(row).fill(null).map(() => new Array(col).fill(0));
    dp[0][0] = matrix[0][0]; // 初始化左上角元素
    // 初始化第一行
    for (var i = 1; i < col; i++) dp[0][i] = dp[0][i - 1] + matrix[0][i];
    // 初始化第一列
    for (var j = 1; j < row; j++) dp[j][0] = dp[j - 1][0] + matrix[j][0];
    // 动态规划
    for (var i = 1; i < row; i++) {
        for (var j = 1; j < col; j++) {
            dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];
        }
    }
    return dp[row - 1][col - 1]; // 右下角元素结果即为答案
}

背包

01背包

n件物品,重量为w[i],价值为c[j]，容量为V的，其中每种物品都只有1件。
dp[i][v]表示前i件物品(1≤i≤n, 0≤v≤V)恰好装入容量为v的背包中所能获得的最大价值。

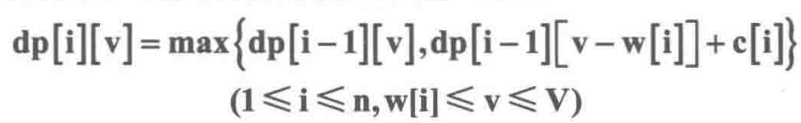
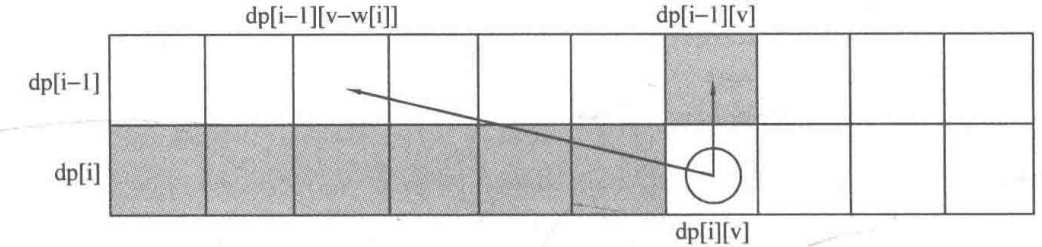
完全背包

与01背包问题不同的是其中每种物品都有无数件。

技巧

不用顺着题目思路来

输入的是一个单链表，让我分组翻转链表，而且还特别强调要用递归实现，就是我们旧文 K 个一组翻转链表 的算法。嗯，如果用数组进行翻转，两分钟就写出来了，嘿嘿。

还有我们前文 扁平化嵌套列表 讲到的题目，思路很巧妙，但是在笔试中遇到时，输入是一个形如 [1,[4,[6]]] 的字符串，那直接用正则表达式把数字抽出来，就是一个扁平化的列表了

输出为值（eg：Yes/No）

时间复杂度

logN，二分查找

MN，嵌套 for 循环/二维动态规划

数据规模

 0 < n < 10，那很明显这个题目的复杂度很高，可能是指数或者阶乘级别的，因为数据规模再大一点它的判题系统就算不过来了嘛，这种题目十有八九就是回溯算法暴力穷举就完事。

面试手撕

合法的URL

URL结构一般包括协议、主机名、主机端口、路径、请求信息、哈希

1. 域名不区分大小写："www"子域名（可选）、二级域名、"com"顶级域名
2. 只能包含字母（a-z、A-Z）、数字（0-9）和连字符（-）（但-不能再首尾）

https://www.bilibili.com/video/BV1F54y1N74E/?spm_id_from=333.337.search-card.all.click&vd_source=6fd32175adc98c97cd87300d3aed81ea
//开始:                     ^
//协议:                     http(s)?:\/\/
//域名:                     [a-zA-Z0-9]+-[a-zA-Z0-9]+|[a-zA-Z0-9]+
//顶级域名 如com cn,2-6位:   [a-zA-Z]{2,6}
//端口 数字:                (:\d+)?
//路径 任意字符 如 /login:   (\/.+)?
//哈希 ? 和 # ，如?age=1:    (\?.+)?(#.+)?
//结束:                      $
//     https://           www.bilibili                com    /video/BV1F54y1N74E  ?spm..            
/^(http(s)?:\/\/)?(([a-zA-Z0-9]+-[a-zA-Z0-9]+|[a-zA-Z0-9]+)\.)+([a-zA-Z]{2,6})(:\d+)?(\/.+)?(\?.+)?(#.+)?$/.test(url)

千位分割

  const format = (n) => {
        let num = n.toString() // 拿到传进来的 number 数字 进行 toString
        let len = num.length // 在拿到字符串的长度
        // 当传进来的结果小于 3 也就是 千位还把结果返回出去 小于3 不足以分割
        if (len < 3) {
            return num
        } else {
            let render = len % 3 //传入 number 的长度 是否能被 3 整除
            if (render > 0) { // 说明不是3的整数倍
                return num.slice(0, render) + ',' + num.slice(render, len).match(/\d{3}/g).join(',')
            } else {
                return num.slice(0, len).match(/\d{3}/g).join(',')
            }
        }
    }

    let str = format(298000)
    console.log(str)

常用方法/值

Math/Number

//e=2.718281828459045
Math.E;

//绝对值
Math.abs()

//基数（base）的指数（exponent）次幂，即 base^exponent。
Math.pow(base, exponent)


//max,min不支持传递数组
Math.max(value0, value1, /* … ,*/ valueN)
Math.max.apply(null,array)
//apply会将一个数组装换为一个参数接一个参数
//null是因为没有对象去调用这个方法,只需要用这个方法运算


//取整
Math.floor()  向下取一个整数（floor地板）
Math.ceil()  向上取一个整数（ceil天花板）
Math.round() 返回一个四舍五入的值
Math.trunc() 直接去除小数点后面的值

Number.MAX_VALUE 
Number.MIN_VALUE;

Map（set\delete\get\has）

保存键值对，

任何值（函数、对象、基本类型）都可以作为键/值。
object的键必须是一个String或是Symbol 。

const contacts = new Map()
contacts.set('Jessie', {phone: "213-555-1234", address: "123 N 1st Ave"})
contacts.has('Jessie') // true
contacts.get('Hilary') // undefined
contacts.delete('Jessie') // true
console.log(contacts.size) // 1

function logMapElements(value, key, map) {
  console.log(`m[${key}] = ${value}`);
}

new Map([['foo', 3], ['bar', {}], ['baz', undefined]])
  .forEach(logMapElements);

// Expected output: "m[foo] = 3"
// Expected output: "m[bar] = [object Object]"
// Expected output: "m[baz] = undefined"

Set（add/delete/has）

值的集合，且值唯一

let setPos = new Set(); 
setPos.add(value);//Boolean
setPos.has(value);
setPos.delete(value);

function logSetElements(value1, value2, set) {
  console.log(`s[${value1}] = ${value2}`);
}

new Set(['foo', 'bar', undefined]).forEach(logSetElements);

// Expected output: "s[foo] = foo"
// Expected output: "s[bar] = bar"
// Expected output: "s[undefined] = undefined"

set判断===相等*

//Set用===判断是否相等
const set= new Set();
const obj1={ x: 10, y: 20 },obj2={ x: 10, y: 20 }
set.add(obj1).add(obj2);

console.log(obj1===obj2);//false
console.log(set.size);// 2

set.add(obj1);
console.log(obj1===obj1);//true
console.log(set.size);//2

Array

输出arr->srting：arr.join(separator)  arr.toString()

初始化数组：new Array(length).fill(value)

增删：arr.(un)shift/pop/splice(start,delCnt,item...)

arr.includes()

array.findIndex(item => item >30);

array.find(item => item> 30);

查询（时间复杂度和手动遍历一样）

//创建字符串
//join() 方法将一个数组（或一个类数组对象）的所有元素连接成一个字符串并返回这个字符串，
//用逗号或指定的分隔符字符串分隔。如果数组只有一个元素，那么将返回该元素而不使用分隔符。
Array.join()
Array.join(separator)

//################创建数组：
//伪数组转成数组
Array.from(arrayLike, mapFn)
console.log(Array.from('foo'));
// Expected output: Array ["f", "o", "o"]

console.log(Array.from([1, 2, 3], x => x + x));
// Expected output: Array [2, 4, 6]

console.log( Array.from({length:3},(item, index)=> index) );// 列的位置
// Expected output:Array [0, 1, 2]


//################原数组会改变：

arr.reverse()//返回翻转后的数组

// 无函数
//即升序
arr.sort()//默认排序顺序是在将元素转换为字符串，然后比较它们的 UTF-16
// 比较函数
arr.sort(compareFn)
function compareFn(a, b) {
  if (在某些排序规则中，a 小于 b) {
    return -1;
  }
  if (在这一排序规则下，a 大于 b) {
    return 1;
  }
  // a 一定等于 b
  return 0;
}
//升序
function compareNumbers(a, b) {
  return a - b;
}


//固定值填充
arr.fill(value)
arr.fill(value, start)
arr.fill(value, start, end)


//去除
array.shift() //从数组中删除第一个元素，并返回该元素的值。

array.pop() //从数组中删除最后一个元素，并返回该元素的值。
array.push() //将一个或多个元素添加到数组的末尾，并返回该数组的新长度

//unshift() 方法将一个或多个元素添加到数组的开头，并返回该数组的新长度
array.unshift(element0, element1, /* … ,*/ elementN)

//粘接，通过删除或替换现有元素或者原地添加新的元素来修改数组，并以数组形式返回被修改的内容。
array.splice(start)
array.splice(start, deleteCount)
array.splice(start, deleteCount, item1)
array.splice(start, deleteCount, item1, item2...itemN)

//################原数组不会改变：

//切片，浅拷贝（包括 begin，不包括end）。
array.slice()
array.slice(start)
array.slice(start, end)

//展平，按照一个可指定的深度递归遍历数组，并将所有元素与遍历到的子数组中的元素合并为一个新数组返回。
array.flat()//不写参数默认一维
array.flat(depth)

//过滤器，函数体 为 条件语句
// 箭头函数
filter((element) => { /* … */ } )
filter((element, index) => { /* … */ } )
filter((element, index, array) => { /* … */ } )
array.filter(str => str .length > 6) 

//遍历数组处理
// 箭头函数
map((element) => { /* … */ })
map((element, index) => { /* … */ })
map((element, index, array) => { /* … */ })
array.map(el => Math.pow(el,2))
//map和filter同参

//接收一个函数作为累加器，数组中的每个值（从左到右）开始缩减，最终计算为一个值。
// 箭头函数
reduce((previousValue, currentValue) => { /* … */ } )
reduce((previousValue, currentValue, currentIndex) => { /* … */ } )
reduce((previousValue, currentValue, currentIndex, array) => { /* … */ } )
reduce((previousValue, currentValue) => { /* … */ } , initialValue)
reduce((previousValue, currentValue, currentIndex) => { /* … */ } , initialValue)
array.reduce((previousValue, currentValue, currentIndex, array) => { /* … */ }, initialValue)

//一个“reducer”函数，包含四个参数：
//previousValue：上一次调用 callbackFn 时的返回值。
//在第一次调用时，若指定了初始值 initialValue，其值则为 initialValue，
//否则为数组索引为 0 的元素 array[0]。

//currentValue：数组中正在处理的元素。
//在第一次调用时，若指定了初始值 initialValue，其值则为数组索引为 0 的元素 array[0]，
//否则为 array[1]。

//currentIndex：数组中正在处理的元素的索引。
//若指定了初始值 initialValue，则起始索引号为 0，否则从索引 1 起始。

//array：用于遍历的数组。

//initialValue 可选
//作为第一次调用 callback 函数时参数 previousValue 的值。
//若指定了初始值 initialValue，则 currentValue 则将使用数组第一个元素；
//否则 previousValue 将使用数组第一个元素，而 currentValue 将使用数组第二个元素。
const array1 = [1, 2, 3, 4];

// 0 + 1 + 2 + 3 + 4
const initialValue = 0;
const sumWithInitial = array1.reduce(
  (accumulator, currentValue) => accumulator + currentValue,
  initialValue
);

console.log(sumWithInitial);
// Expected output: 10

String

输入str->arr：str.split(separator/reg)

str.substring(indexStart[, indexEnd])

str.indexOf(searchString[, position]) 

str.includes()

str.charAt(index)//获取第n位字符  
str.charCodeAt(n)//获取第n位字符的UTF-16字符编码 （Unicode）A是65，a是97
String.fromCharCode(num1[, ...[, numN]])//根据UTF编码创建字符串

String.fromCharCode('a'.charCodeAt(0))='a'

str.trim()//返回去掉首尾的空白字符后的新字符串

str.split(separator)//返回一个以指定分隔符出现位置分隔而成的一个数组，数组元素不包含分隔符

const str = 'The quick brown fox jumps over the lazy dog.';

const words = str.split(' ');
console.log(words[3]);
// Expected output: "fox"


str.toLowerCase( )//字符串转小写；
str.toUpperCase( )//字符串转大写；

str.concat(str2, [, ...strN])


str.substring(indexStart[, indexEnd])  //提取从 indexStart 到 indexEnd（不包括）之间的字符。
str.substr(start[, length]) //没有严格被废弃 (as in "removed from the Web standards"), 但它被认作是遗留的函数并且可以的话应该避免使用。它并非 JavaScript 核心语言的一部分，未来将可能会被移除掉。

str.indexOf(searchString[, position]) //在大于或等于position索引处的第一次出现。
str.match(regexp)//找到一个或多个正则表达式的匹配。
const paragraph = 'The quick brown fox jumps over the lazy dog. It barked.';
let regex = /[A-Z]/g;
let found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T", "I"]
regex = /[A-Z]/;
found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T"]

//match类似 indexOf() 和 lastIndexOf()，但是它返回指定的值，而不是字符串的位置。
var str = '123123000'
str.match(/\w{3}/g).join(',') // 123,123,000

str.search(regexp)//如果匹配成功，则 search() 返回正则表达式在字符串中首次匹配项的索引;否则，返回 -1
const paragraph = '? The quick';

// Any character that is not a word character or whitespace
const regex = /[^\w\s]/g;

console.log(paragraph.search(regex));
// Expected output: 0

str.repeat(count)//返回副本
str.replace(regexp|substr, newSubStr|function)//返回一个由替换值（replacement）替换部分或所有的模式（pattern）匹配项后的新字符串。
const p = 'lazy dog.Dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replace('dog', 'monkey'));
// "lazy monkey.Dog lazy"


let regex = /dog/i;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replace(regex, 'ferret'));
//"lazy ferret.Dog lazy"

regex = /d|Dog/g;
console.log(p.replace(regex, 'ferret'));
//"lazy ferretog.ferret lazy"

//当使用一个 regex 时，您必须设置全局（“g”）标志， 否则，它将引发 TypeError：“必须使用全局 RegExp 调用 replaceAll”。
const p = 'lazy dog.dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replaceAll('dog', 'monkey'));
// "lazy monkey.monkey lazy"


let regex = /dog/g;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replaceAll(regex, 'ferret'));
//"lazy ferret.ferret lazy"

正则表达式Regular Expression(RegExp) 

str.match(regexp): [values]

str.search(regexp): idx

str.replace(regexp|substr, newSubStr|function)

修饰符：i大小写不敏感

边界量词：^首$尾

考前复习

应该尽可能多的看各种各样的题目，思考五分钟，想不出来解法的话直接看别人的答案。看懂思路就行了，甚至自己写一遍都没必要，因为比较浪费时间。

笔试的时候最怕的是没思路，所以把各种题型都过目一下，起码心里不会慌，只要有思路，平均一道题二三十分钟搞定还是不难的

突击笔试计划

mirrors / youngyangyang04 / leetcode-master · GitCode