目录
一、选择题
二、编程题
三、选择题题解
四、编程题题解
一、选择题
1、设一个有序的单链表中有n个结点,现要求插入一个新结点后使得单链表仍然保持有序,则该操作的时间复杂度()
A. O(log2n)
B. O(1)
C. O(n2)
D. O(n)
2、在一个单链表中,若删除 P 所指结点的后续结点,则执行?
A. p = p->next;p->next = p->next->next;
B. p->next = p->next;
C. p->next = p->next->next;
D. p = p->next->next
3、设一个链表最常用的操作是在末尾插入结点和删除尾结点,则选用()最节省时间
A. 带头结点的双循环链表
B. 单循环链表
C. 带尾指针的单循环链表
D. 单链表
4、单链表实现的栈,栈顶指针为Top(仅仅是一个指针),入栈一个P节点时,其操作步骤为()
A. Top->next=p;
B. p->next=Top->next;Top->next=p;
C. p->next=Top;Top=p->next;
D. p->next=Top;Top=Top->next;
5、用不带头结点的单链表存储队列,其队头指针指向队头结点,队尾指针指向队尾结点,则在进行出队操作时()
A. 仅修改队头指针
B. 仅修改队尾指针
C. 队头、队尾指针都可能要修改
D. 队头、队尾指针都要修改
6、在具有 2n 个结点的完全二叉树中,叶子结点个数为()
A. n
B. n+1
C. n-1
D. n/2
7、在任意一棵非空二叉排序树T1中, 删除某结点v之后形成二叉排序树 T2,再将v 插入T2形成二叉排序树T3。下列关于T1与T3的叙述中,正确的是( )。
I.若 v 是 T1的叶结点,则 T1 与 T3 不同
II. 若 v 是 T1的叶结点,则 T1与 T3相同
III.若 v 不是 T1 的叶结点,则 T1 与 T3 不同
IV.若v 不是 T1 的叶结点,则 T1 与 T3 相同
A. 仅 I、 III
B. 仅 I、 IV
C. 仅 II、 III
D. 仅 II、 IV
8、下述二叉树中,哪一种满足性质:从任一结点出发到根的路径上所经过的结点序列按其关键字有序()
A. 二叉排序树
B. 哈夫曼树
C. AVL树
D. 堆
9、散列文件使用散列函数将记录的关键字值计算转化为记录的存放地址。由于散列函数不是一对一的关系,所以选择好的( )方法是散列文件的关键。
A. 散列函数
B. 除余法中的质数
C. 冲突处理
D. 散列函数和冲突处理
10、将整数数组(7-6-3-5-4-1-2)按照堆排序的方式原地进行升序排列,请问在第一轮排序结束之后,数组的顺序是()
A. 2-6-3-5-4-1-7
B. 6-2-3-5-4-1-7
C. 6-5-3-2-4-1-7
D. 1-4-7-5-6-3-2
二、编程题
1、洗牌 题目链接

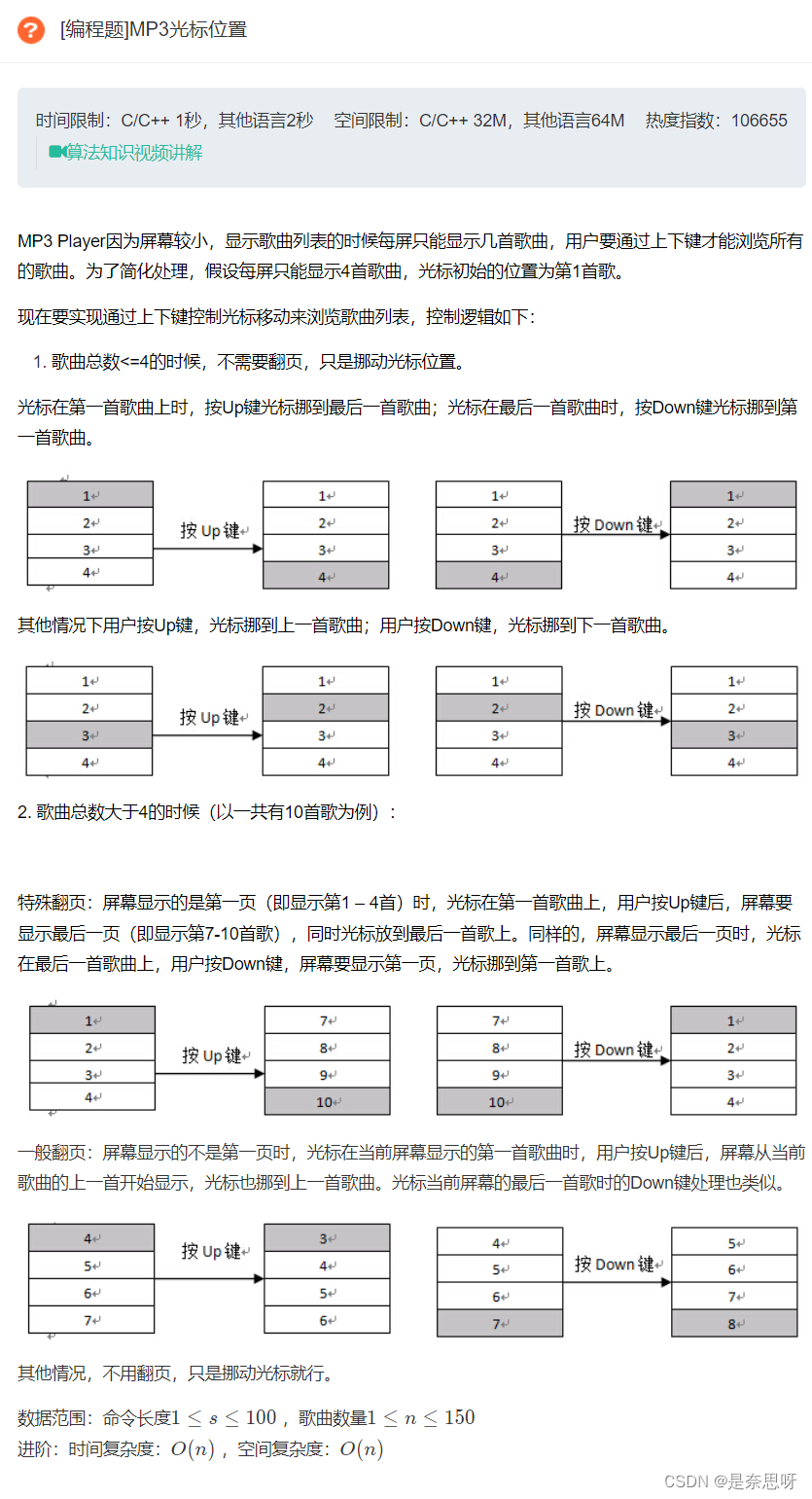
2、MP3光标位置 题目链接
三、选择题题解
1、设一个有序的单链表中有n个结点,现要求插入一个新结点后使得单链表仍然保持有序,则该操作的时间复杂度()
A. O(log2n)
B. O(1)
C. O(n2)
D. O(n)
正确答案:D
题解:
要想插入一个结点保持链表有序就得找到比该节点小的那一个结点,故需要遍历单链表,遍历链表的时间复杂度为O(N),故选D;
2、在一个单链表中,若删除 P 所指结点的后续结点,则执行?
A. p = p->next;p->next = p->next->next;
B. p->next = p->next;
C. p->next = p->next->next;
D. p = p->next->next
正确答案:C
题解:

3、设一个链表最常用的操作是在末尾插入结点和删除尾结点,则选用()最节省时间
A. 带头结点的双循环链表
B. 单循环链表
C. 带尾指针的单循环链表
D. 单链表
正确答案:A
题解:
我们的诉求是最节省时间,当尾部插入结点时我们需要找到最后一个节点,当我们删除最后一个结点时,我们得同时知道倒数第二个结点;
4、单链表实现的栈,栈顶指针为Top(仅仅是一个指针),入栈一个P节点时,其操作步骤为()
A. Top->next=p;
B. p->next=Top->next;Top->next=p;
C. p->next=Top;Top=p->next;
D. p->next=Top;Top=Top->next;
正确答案:B
题解:
我们根据题目知top仅仅只是一个指针,不存数据,当我们实现链栈时,我们肯定选择头部作为栈顶,因为单链表的头插与头删效率最高,具体如下图;

5、用不带头结点的单链表存储队列,其队头指针指向队头结点,队尾指针指向队尾结点,则在进行出队操作时()
A. 仅修改队头指针
B. 仅修改队尾指针
C. 队头、队尾指针都可能要修改
D. 队头、队尾指针都要修改
正确答案:C
题解:
一般情况下,链式队列出队操作只会修改队头结点,但是如果队列中只有一个结点时,如果我们出队,可能也会修改队尾指针;
6、在具有 2n 个结点的完全二叉树中,叶子结点个数为()
A. n
B. n+1
C. n-1
D. n/2
正确答案:A
题解:
根据二叉树的性质,我们可以得到公式n0 = n2 + 1;且n2 + n1 + n0 = 2n;其中n1是只有一个孩子的分支结点,要么为1要么为0,根据这三点求得n0 = n;
7、在任意一棵非空二叉排序树T1中, 删除某结点v之后形成二叉排序树 T2,再将v 插入T2形成二叉排序树T3。下列关于T1与T3的叙述中,正确的是( )。
I.若 v 是 T1的叶结点,则 T1 与 T3 不同
II. 若 v 是 T1的叶结点,则 T1与 T3相同
III.若 v 不是 T1 的叶结点,则 T1 与 T3 不同
IV.若v 不是 T1 的叶结点,则 T1 与 T3 相同
A. 仅 I、 III
B. 仅 I、 IV
C. 仅 II、 III
D. 仅 II、 IV
正确答案:C
题解:
可画图理解,答案选C;
8、下述二叉树中,哪一种满足性质:从任一结点出发到根的路径上所经过的结点序列按其关键字有序()
A. 二叉排序树
B. 哈夫曼树
C. AVL树
D. 堆
正确答案:D
题解:
只有堆才可能会任意节点到根是有序的,如大堆,父节点肯定比子节点大;小堆,父节点肯定比子结点小;
9、散列文件使用散列函数将记录的关键字值计算转化为记录的存放地址。由于散列函数不是一对一的关系,所以选择好的( )方法是散列文件的关键。
A. 散列函数
B. 除余法中的质数
C. 冲突处理
D. 散列函数和冲突处理
正确答案:D
题解:
要完成散列文件必须使用一个契合的哈希函数减少冲突,在冲突出现后也也可以处理冲突;
10、将整数数组(7-6-3-5-4-1-2)按照堆排序的方式原地进行升序排列,请问在第一轮排序结束之后,数组的顺序是()
A. 2-6-3-5-4-1-7
B. 6-2-3-5-4-1-7
C. 6-5-3-2-4-1-7
D. 1-4-7-5-6-3-2
正确答案:C
题解:
以下为一轮排序的步骤;

四、编程题题解
1、洗牌
思路:本题是一道模拟题,看着题目很复杂实际非常简单,一轮洗牌就是将后一半的牌与前一半的牌从后往前依次重新排序;
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int T = 0;
cin >> T;
// T组数据
while(T--)
{
int n, k;
cin >> n >> k;
vector<int> cards;
cards.resize(2 * n, 0);
for(int i = 0; i < 2 * n; i++)
{
cin >> cards[i];
}
// 经过k次洗牌
while(k--)
{
int end1 = n - 1;
int end2 = 2 * n - 1;
int end = 2 * n - 1;
vector<int> tmp(2 * n, 0);
while(end1 >= 0)
{
tmp[end--] = cards[end2--];
tmp[end--] = cards[end1--];
}
cards.swap(tmp);
}
// 遍历
for(auto e : cards)
cout << e << " ";
cout << endl;
}
return 0;
}2、MP3光标位置
思路:本题也是一道模拟题,我们只要模拟出每一种情况即可;这种题的难度在于逻辑是否清晰;
#include <iostream>
#include <string>
using namespace std;
void print_song_list(int num, string& command)
{
int begin = 1;
int end = 0;
int select = 1;
if(num <= 4)
{
end = num;
for(int i = 0; i < command.size(); i++)
{
if(command[i] == 'U')
{
select = select - 1;
if(select == 0) select = num;
}
else
{
select = select + 1;
if(select == num + 1) select = 1;
}
}
}
else
{
// 多页情况
end = 4;
for(auto ch : command)
{
if(ch == 'U')
{
// 向上分为三种情况
// 1、当前光标在第一个位置
// 2、当前光标与begin位置相同
// 3、当前光标与begin位置不同
if(select == 1)
{
select = num;
begin = num - 4 + 1;
end = num;
}
else if(select == begin)
{
select--;
begin--;
end--;
}
else
{
select--;
}
}
else
{
// 向下分为三种情况
// 1、当前光标在第最后一个位置
// 2、当前光标与end位置相同
// 3、当前光标与end位置不同
if(select == num)
{
select = 1;
begin = 1;
end = 4;
}
else if(select == end)
{
select++;
begin++;
end++;
}
else
{
select++;
}
}
}
}
for(int i = begin; i <= end; i++)
cout << i << " ";
cout << endl;
cout << select << endl;
}
int main()
{
int num;
string command;
cin >> num >> command;
print_song_list(num, command);
return 0;
}