什么是数据可视化?
数据可视化是指通过图表、图形、地图等视觉元素将数据呈现出来的过程。它是将抽象的、复杂的数据转化为直观、易于理解的视觉表达的一种方法。数据可视化的目的是帮助人们更好地理解数据,从中发现模式、趋势、关联和异常,从而作出更明智的决策。
数据可视化在各个领域都有广泛的应用,包括商业、科学、工程、医疗、社会科学等。通过可视化数据,我们可以更好地探索数据之间的关系,展示数据的变化趋势,发现数据的异常值,并从中得出洞察和结论。
常见的数据可视化形式包括:
-
折线图和曲线图:用于显示随时间或其他连续变量的趋势和变化。
-
条形图和柱状图:用于比较不同类别或组之间的数据。
-
饼图和环形图:用于显示组成部分的相对比例。 散点图:用于展示两个变量之间的关系和分布。
-
热力图:用于显示数据在二维空间上的密度和分布情况。
-
地图可视化:将数据以地理位置为基础展示在地图上,用于显示地理分布和空间相关性。
-
仪表盘:集成多种图表和指标,用于提供全面的数据概览。
数据可视化不仅使数据更易于理解和交流,而且有助于发现隐藏在数据中的模式和见解,从而对业务和决策产生积极的影响。然而,数据可视化也需要注意设计和解释,以确保传达的信息准确、清晰且不误导。
直方图
直方图是一种常见的数据可视化图表,用于显示连续变量的分布情况。它将数据划分为若干个等距的区间(称为“箱子”或“柱”),并计算每个区间内数据点的频数(或频率),然后将这些频数用柱状图表示。
直方图的横轴表示连续变量的取值范围,纵轴表示频数(或频率,即频数与总样本数之比)。每个柱子的宽度表示区间的范围,柱子的高度表示该区间内数据点的数量或频率。
直方图的主要用途
是展示数据的分布情况,帮助我们理解数据集中值的范围、数据点的密度和分布模式。通过直方图,我们可以快速获得以下信息:
- 数据的中心趋势:通过直方图的峰值可以了解数据的主要集中区域。
- 数据的离散程度:直方图的宽度和峰值陡峭程度可以显示数据的分散程度。
- 数据的异常值:通过观察直方图的尾部可以发现异常值或离群点。
- 数据的分布形态:直方图的形状可以显示数据的分布模式,如正态分布、偏态等。
绘制直方图的步骤包括:
- 确定数据集的范围和区间数量。
- 将数据划分到对应的区间,并计算每个区间内数据点的频数或频率
- 绘制柱状图,横轴表示区间,纵轴表示频数或频率。
- 可选地添加标题、标签和图例等,以增加图表的可读性和易理解性。
直方图是一种简单而强大的数据可视化工具,适用于各种类型的数据,尤其是连续变量的分布展示和对比分析。
废话不多说,下面用Python中的matplotlib库来实现 直方图
import matplotlib.pyplot as plt
# 示例数据:学生考试成绩
exam_scores = [65, 78, 89, 92, 77, 82, 90, 88, 95, 72, 85, 78, 84, 79, 87, 91, 70, 94, 83, 76]
# 设置直方图的间隔(bin)
bin_width = 5
# 绘制直方图
plt.hist(exam_scores, bins=range(min(exam_scores), max(exam_scores) + bin_width, bin_width), edgecolor='black')
# 添加标题和标签
plt.title('Exam Scores Histogram')
plt.xlabel('Scores')
plt.ylabel('Frequency')
# 显示图表
plt.show()
运行结果:
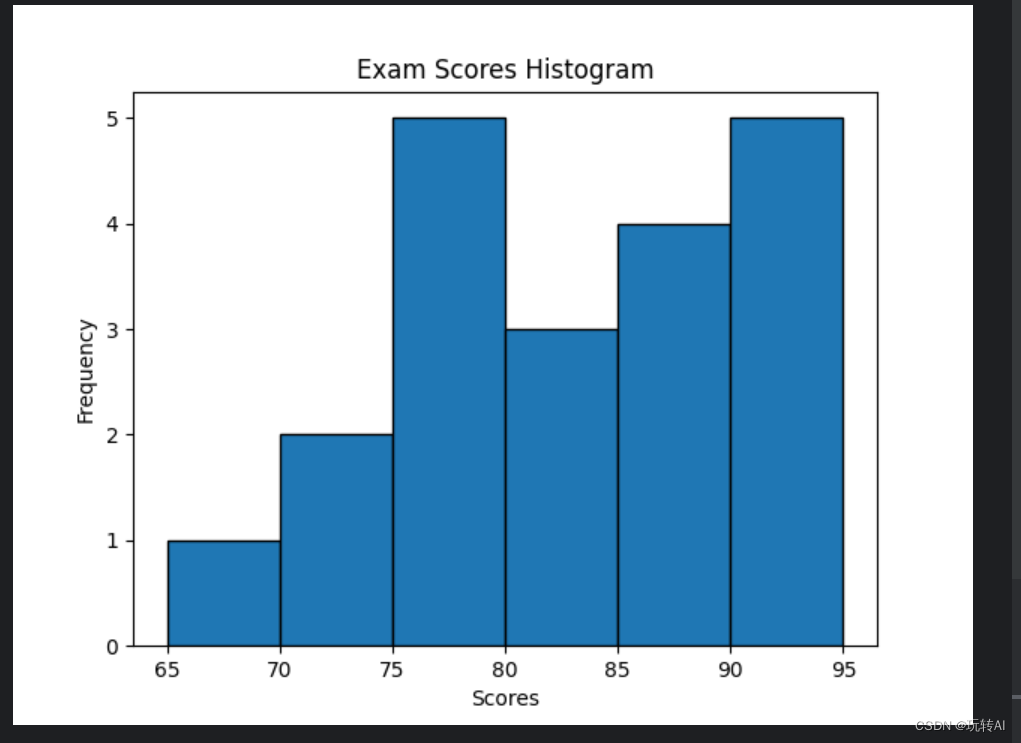
在这个示例中,我们将成绩数据exam_scores分成了5 分为一组的间隔,然后通过plt.hist()函数绘制了直方图。横轴表示成绩区间,纵轴表示在每个区间内的学生数量(频数)。
从这个图中我们很快得就知道65 到70 之间分数得同学 就一个,70 到75 得成绩得学生有2 个, 为了对这个图表得理解 我们可以手动得修改数据去看看图表得变化,比如 往数组中 加个67 再来看看图标得变化
# 示例数据:学生考试成绩
exam_scores = [65,67,78, 89, 92, 77, 82, 90, 88, 95, 72, 85, 78, 84, 79, 87, 91, 70, 94, 83, 76]
再次运行得图表
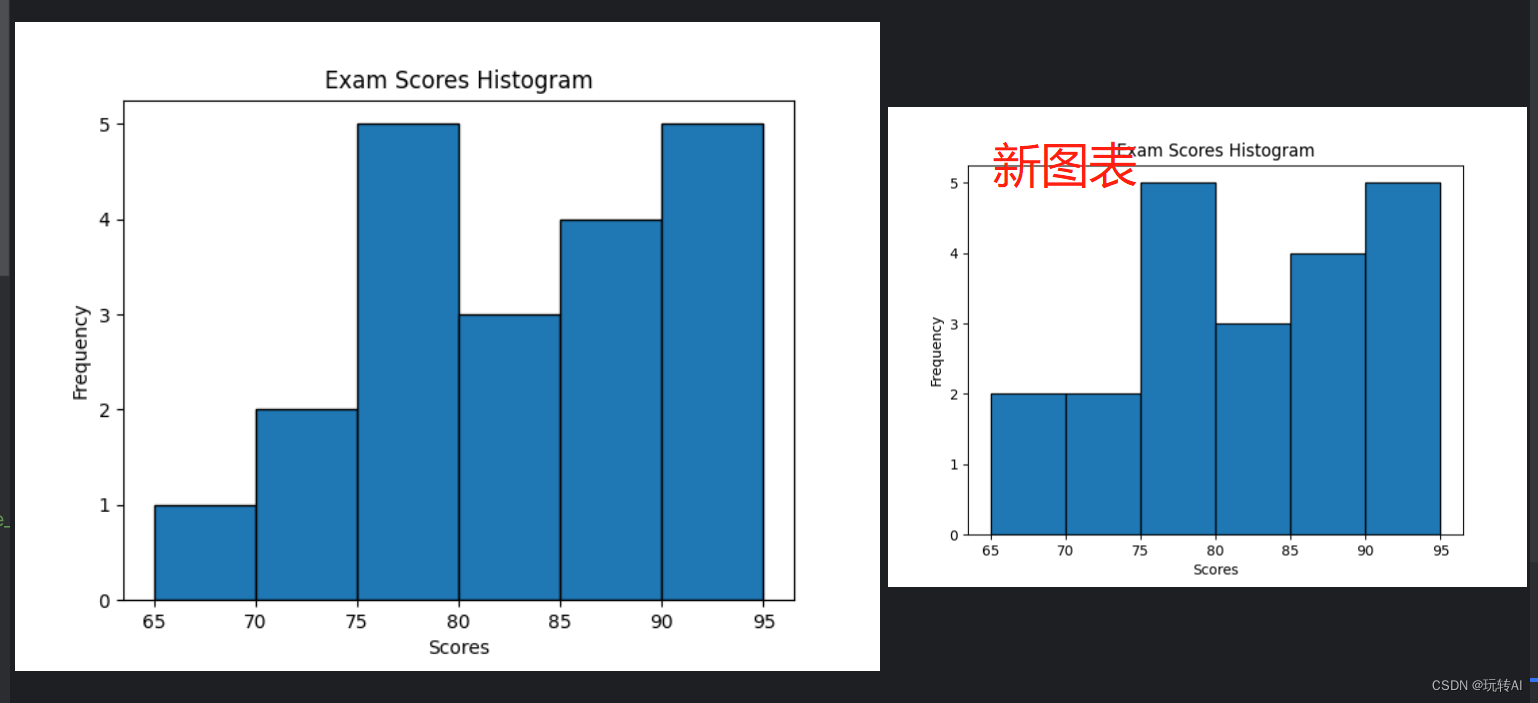
很明显,新图标中 65到70 得区间得数据 增加到2 了,
经过上面 得操作后 我们对直方图的概念以及应用有了一定的理解和实操,接下来 我们就对pima 这个数据集来进行实操,看看效果
代码如下:
import pandas as pd
from matplotlib import pyplot as plt
#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)
data.hist()
plt.show()
运行效果如下:
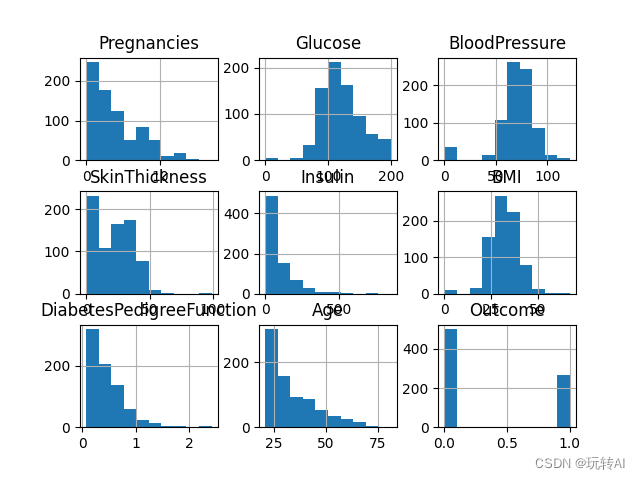
从这个图我们先不看数据,看坐标就发现横坐标与字段描述 位置冲突了
解决方案
plt.tight_layout()
新代码:
import pandas as pd
from matplotlib import pyplot as plt
#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)
data.hist()
#设置布局自适应
plt.tight_layout()
plt.show()
运行效果:
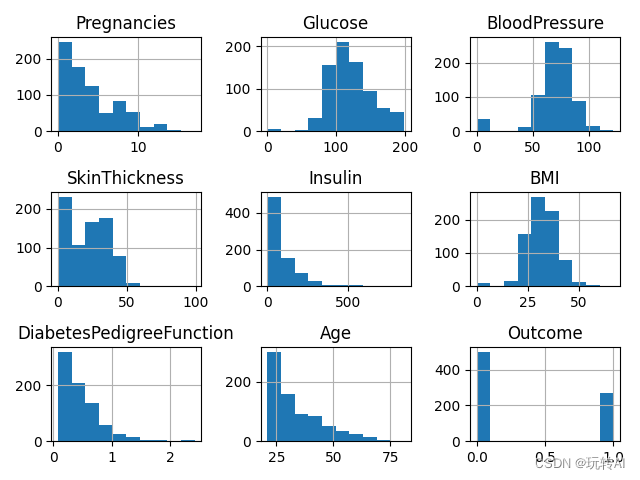
这样显示正常了,我们看到有9个直方图,分别对应数据集中 9列数据的直方图
从 Outcome 这个直方图中我们很容易的可以看出1得糖尿病得人大概是200 多,不会得得是400 以上.因为就两个区间值比较明显,就2个值,可以再分析下age 这个图,从这个图中我们也可以单独得获取这个年龄得图,代码如下:
import pandas as pd
from matplotlib import pyplot as plt
from pandas import set_option
#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)
# 设置直方图的间隔(bin)
bin_width = 5
glucose_values = data['Age']
# 绘制直方图
plt.hist(glucose_values, bins=range(min(glucose_values), max(glucose_values) + bin_width, bin_width), edgecolor='black')
plt.tight_layout()
plt.show()
运行结果:
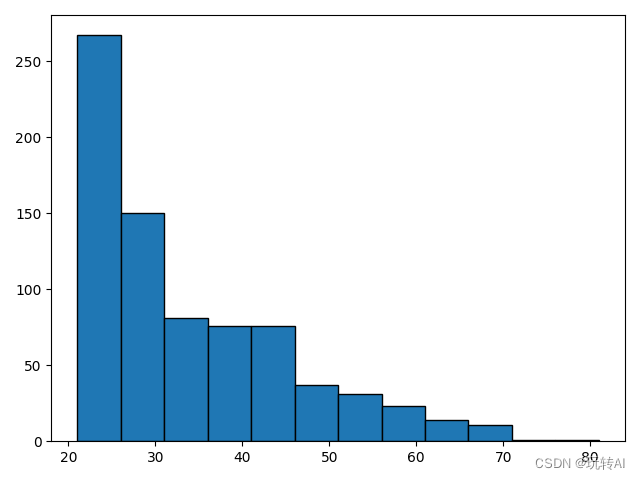
密度图
密度图(Density Plot)是一种用于可视化数据分布的图表,它类似于直方图,但使用连续的曲线来表示数据的分布。密度图通过估计数据的概率密度函数,反映了数据在整个取值范围内的分布情况。密度图可以帮助我们更直观地了解数据的概率密度和分布特征。
在绘制密度图之前,我们需要对数据进行核密度估计(Kernel Density Estimation,KDE)。核密度估计是一种非参数方法,它通过在每个数据点周围放置核(通常是高斯核)来估计数据的概率密度函数。
在Python中,你可以使用seaborn或matplotlib库来绘制密度图。
示例代码:
import pandas as pd
from matplotlib import pyplot as plt
#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)
data.plot(kind='density', subplots=True, layout=(3, 3), sharex=False)
# 设置布局自适应
plt.tight_layout()
plt.suptitle('Density Plot');
plt.show()
运行结果图示:
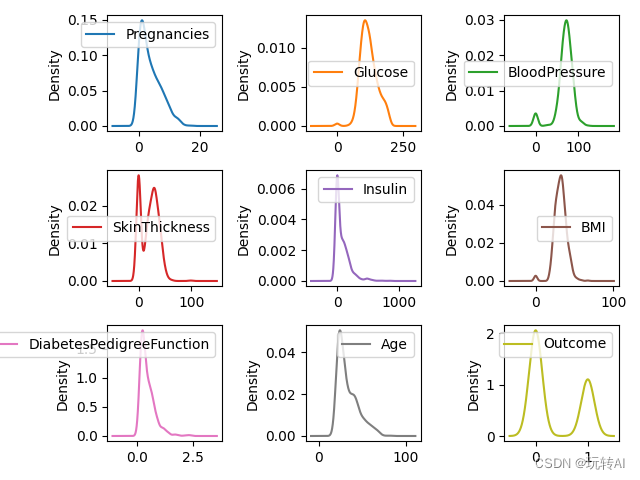
这段代码参数得含义
data.plot(kind='density', subplots=True, layout=(3, 3), sharex=False)
kind:该参数指定要创建的图表类型。在这里,我们设置为kind=‘density’,表示要创建每个列的密度图。
subplots:当设置为True时,该参数将为DataFrame中的每个列创建独立的子图。每个子图将表示一个列的密度图。在代码中,我们设置subplots=True来创建子图。
layout:该参数以元组(行数, 列数)的形式指定子图的布局。在代码中,我们设置layout=(3, 3),表示创建一个3行3列的网格布局,也就是共有3行和3列的子图。
sharex:当设置为False时,该参数确保每个子图都有自己的x轴范围。如果设置为True,所有子图将共享相同的x轴范围。在代码中,我们使用sharex=False,以便每个子图有独立的x轴范围。
plt.suptitle('Density Plot');
title:通过suptitle()函数在整个图表顶部添加一个总标题。在代码中,我们使用plt.suptitle(‘每个列的密度图’, y=1.02)添加一个总标题。
综上所述,这段代码创建了一个3x3的网格布局,其中每个子图代表DataFrame data 中的一个列的密度图。subplots=True 确保每个列都有自己的子图,layout=(3, 3)定义了子图的排列方式。sharex=False确保每个子图有自己的x轴范围,suptitle()函数添加了一个总标题在整个图表的顶部。
当然也可以对单个数据进行密度图分析,自己动手来试试!
箱线图
箱线图(Box
Plot),也称为盒须图或盒式图,是一种用于可视化数据分布和识别异常值的图表。它展示了数据的中位数、上下四分位数、最小值、最大值和可能的异常值。
箱线图的构成要素包括:
箱体(Box):在图表的中间部分,表示数据的上下四分位数(Q1和Q3)。箱体的长度是数据的四分位距(IQR = Q3 - Q1),箱体内部的线表示数据的中位数(或者称为Q2)。
须(Whiskers):从箱体延伸出来的线段,通常表示数据的范围。标准的箱线图会将须延伸至最小值和最大值,但也可以根据需要使用其他规则。
异常值(Outliers):超出须的范围的数据点,通常是异常值。
箱线图可以帮助我们快速了解数据的分布情况,以及数据中是否存在异常值或离群点。
在Python中,你可以使用seaborn或matplotlib库绘制箱线图。以下是使用seaborn库的示例代码:
import seaborn as sns
import matplotlib.pyplot as plt
# 示例数据:假设这是"Glucose"(血糖)的数据
glucose_values = [300,148, 85, 183, 80, 137, 116, 78, 115, 197, 125, 110, 168, 139, 189]
# 使用seaborn绘制箱线图
sns.boxplot(x=glucose_values)
# 添加标题和标签
plt.title('Glucose Box Plot')
plt.xlabel('Glucose')
plt.ylabel('YGlucose')
# 显示图表
plt.show()
运行效果:
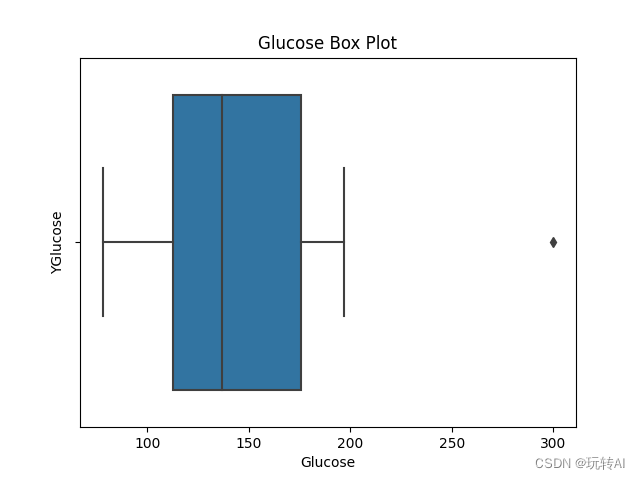
看图中得300 就是异常点或者可以说是数据得突出点.
基于Pima 数据集得箱线图
import pandas as pd
from matplotlib import pyplot as plt
#数据预处理
path = 'D:\down\\archive\\diabetes.csv'
data = pd.read_csv(path)
data.plot(kind='box', subplots=True, layout=(3, 3), sharex=False,)
plt.suptitle('Density Plot');
# 设置布局自适应
plt.tight_layout()
plt.show()
运行结果:
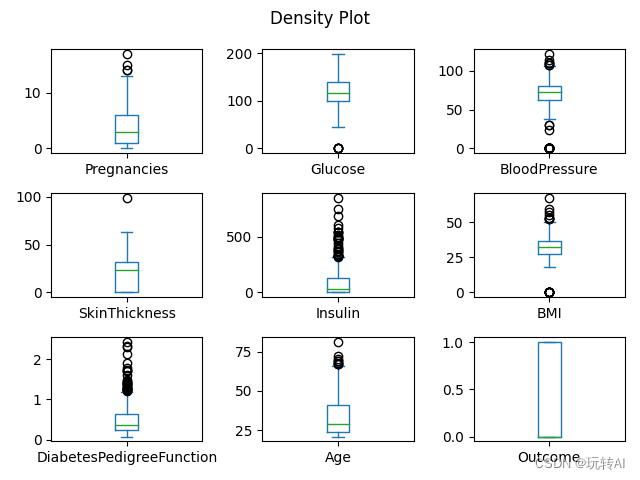
这里就简单介绍这几种吧,类似得图表还有很多,要熟悉图表 不能光看,动手实验看懂 对看懂各个图表 会事半功倍!