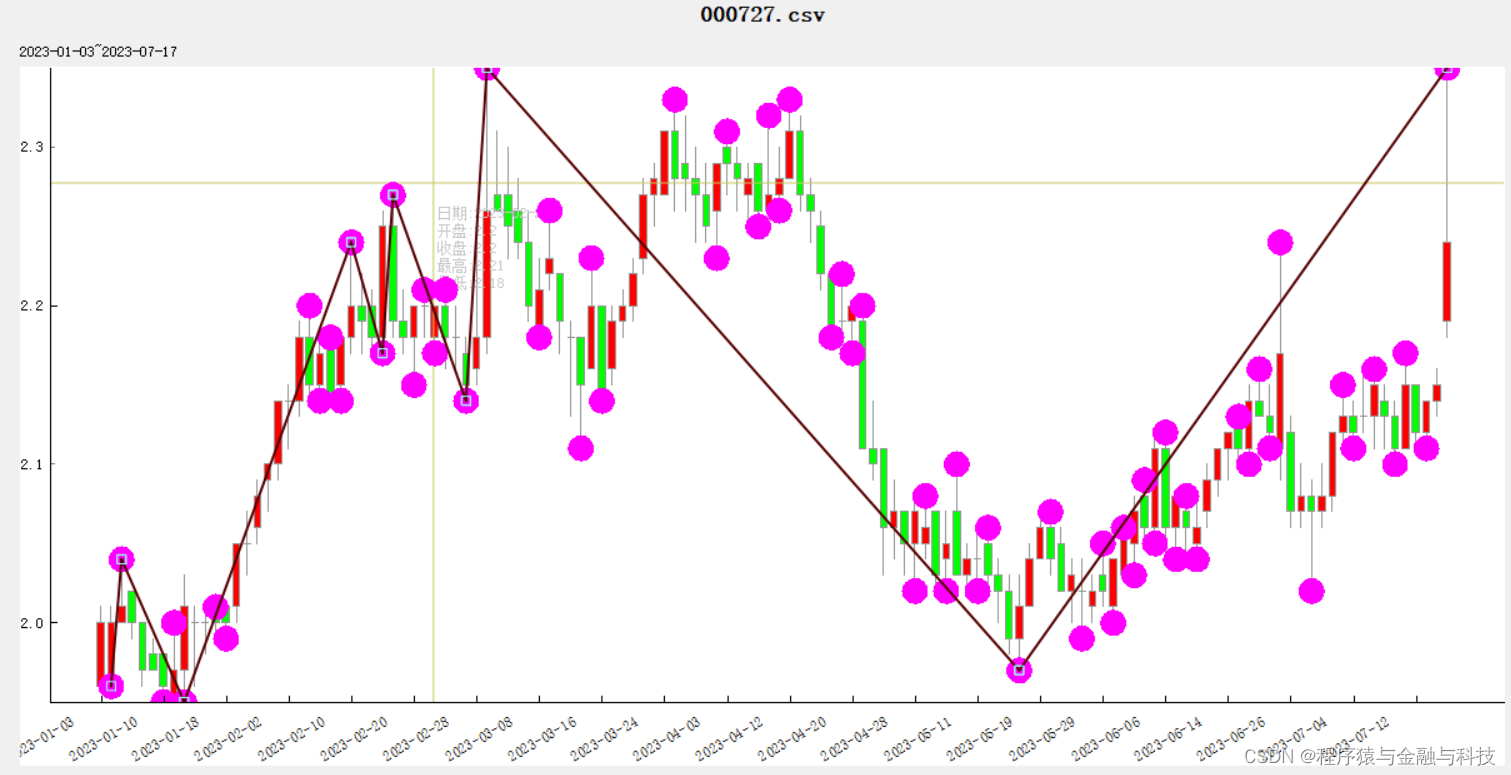
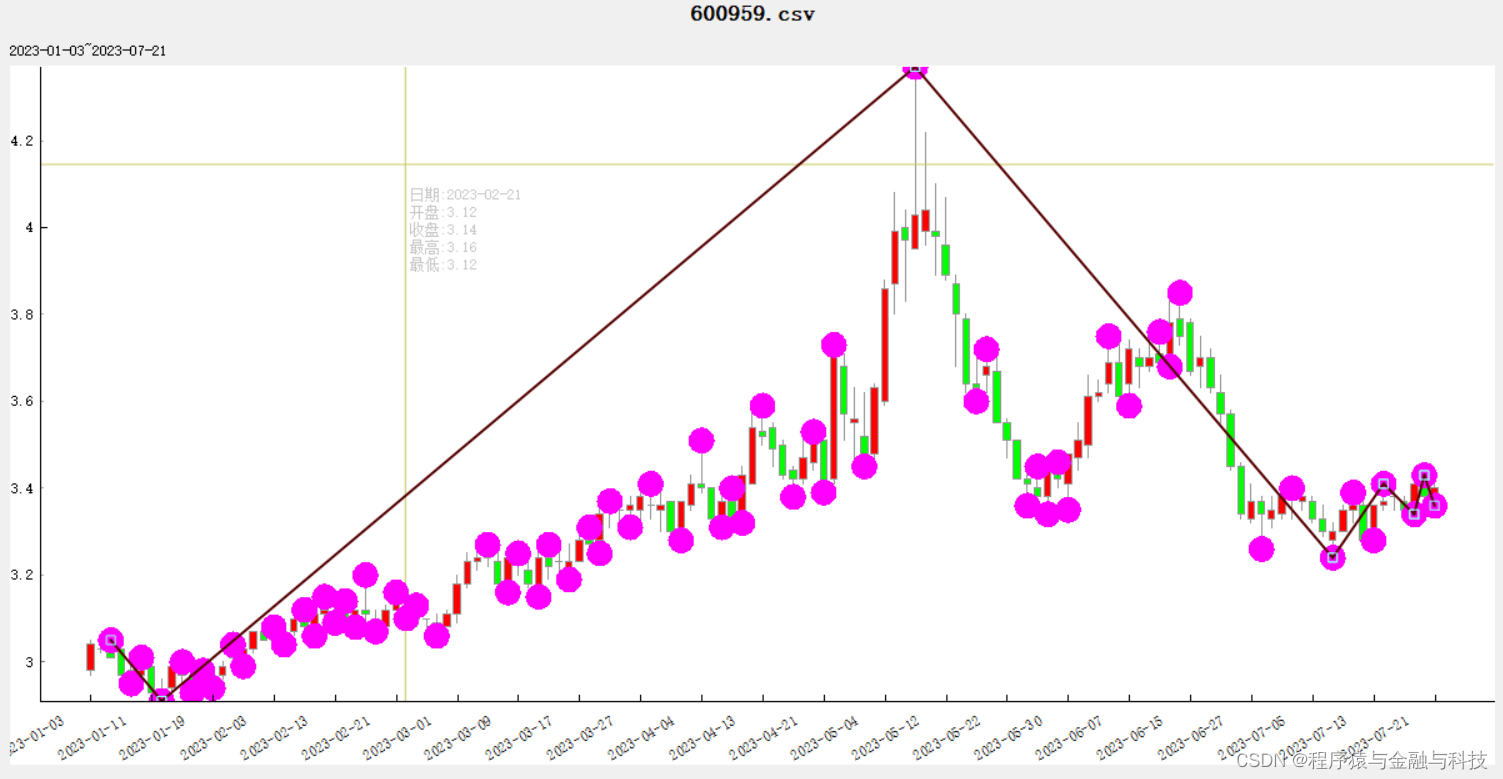
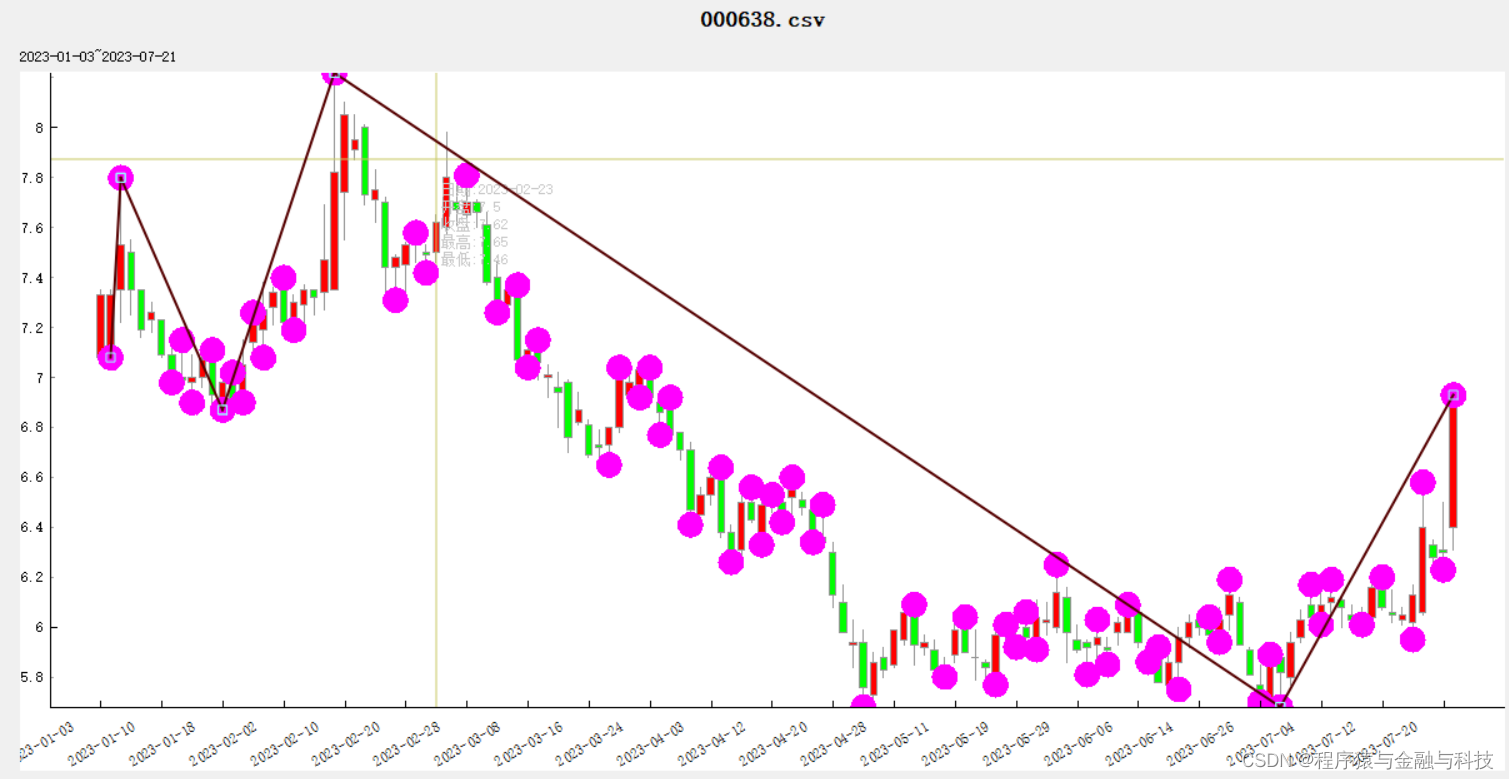
承接 【python_在K线找出波段_01_找出所有转折点】博文
地址:python_在K线找出波段_01_找出所有转折点_程序猿与金融与科技的博客-CSDN博客
目录
写在前面:
寻找波段的逻辑:
寻找方法
判断高低点连线是否有效
判断方法:
判断点相对连线位置的方法:
代码:
计算一元一次方程a b值方法
定位下一个转折点方法
判断点相对连线位置方法
向左右两个方向反复寻找方法
主方法
运用并验证结果
写在前面:
在K线找出波段分两大步骤
步骤一:找出所有转折点
步骤二:找出波段
步骤一已经在【python_在K线找出波段_01_找出所有转折点】博文中表述,步骤二要在步骤一的基础上画出波段,由于波段的确认有很强的主观性,本文找波段只是提供一种方法,大家可以根据自己对波段的理解对代码进行修改。
寻找波段的逻辑:
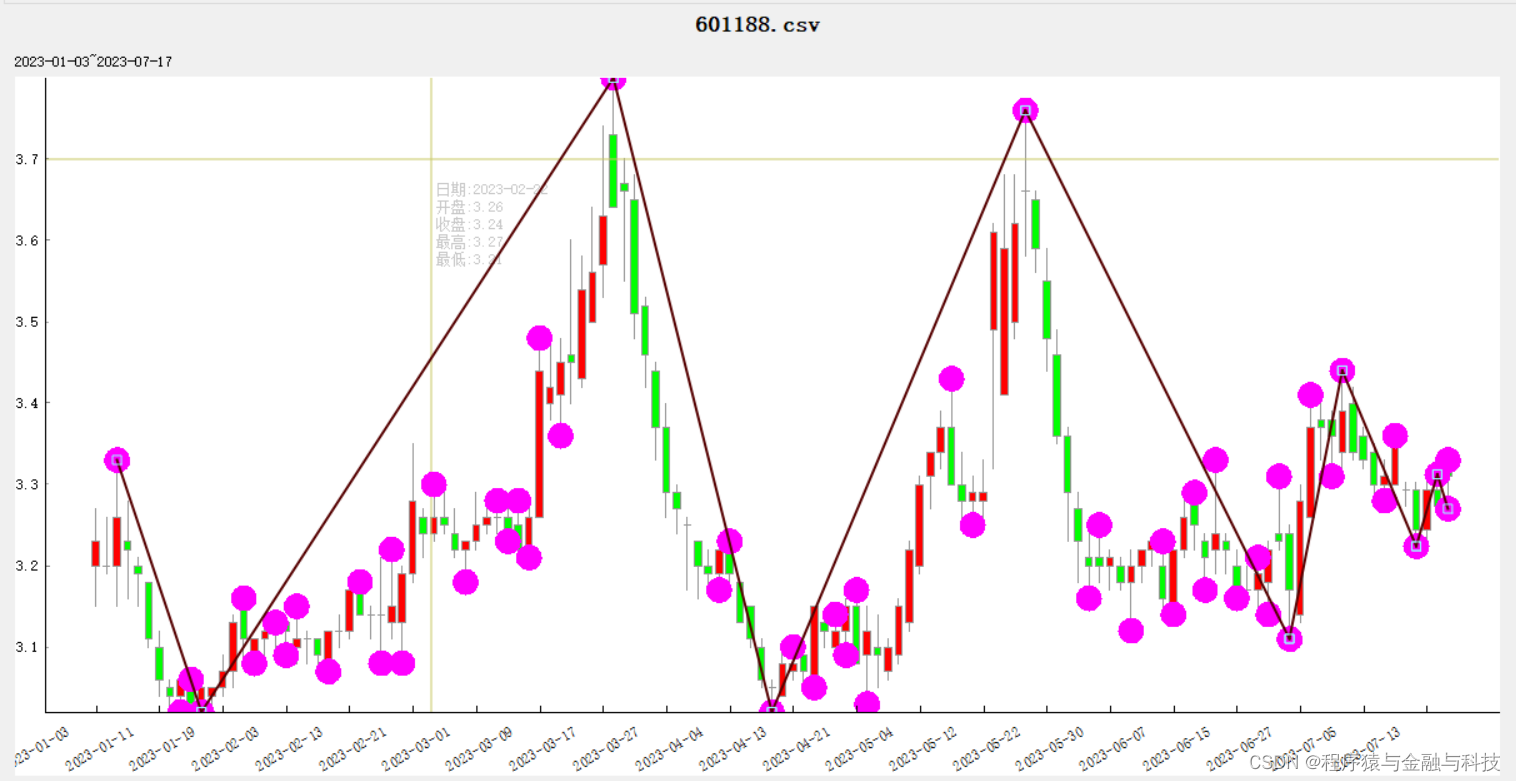
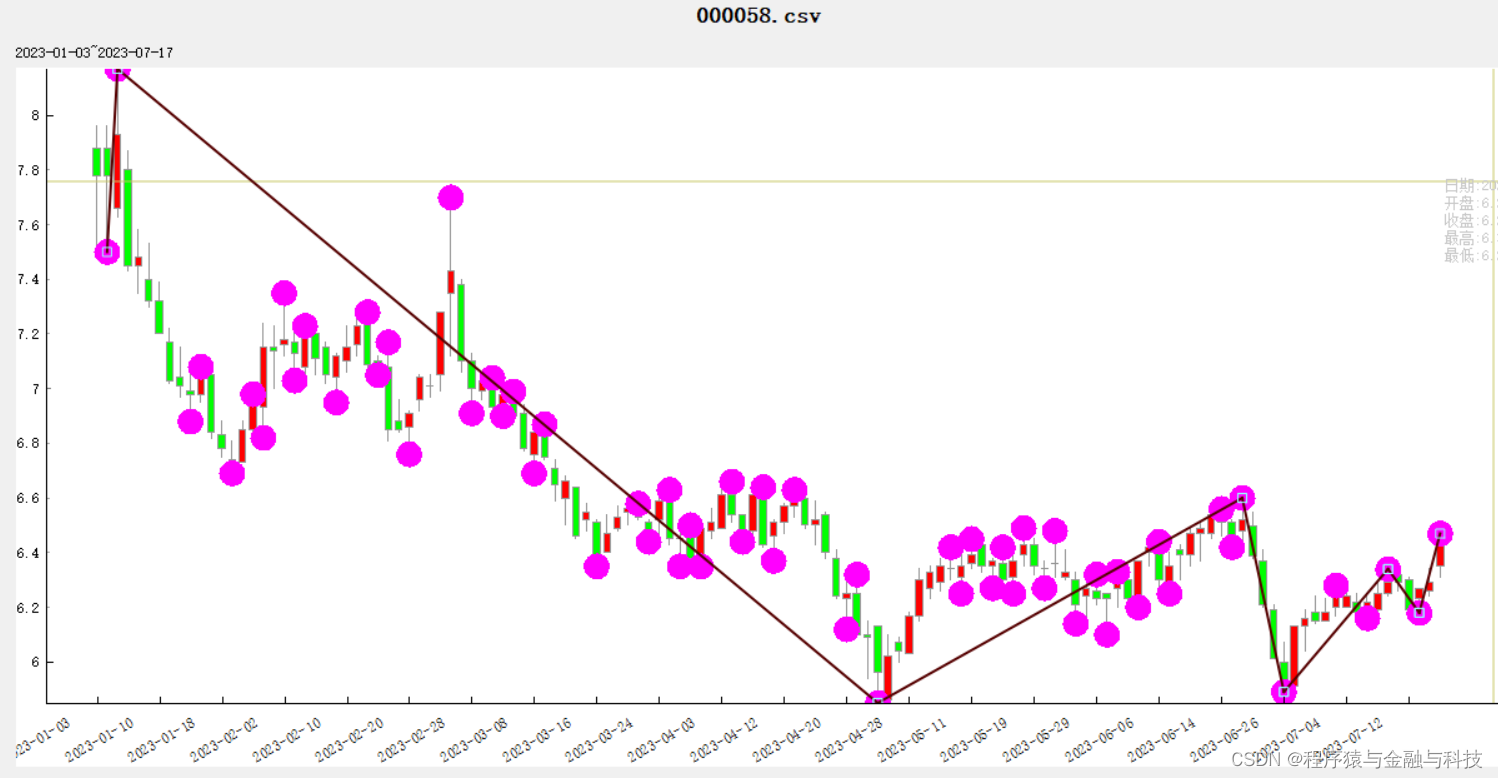
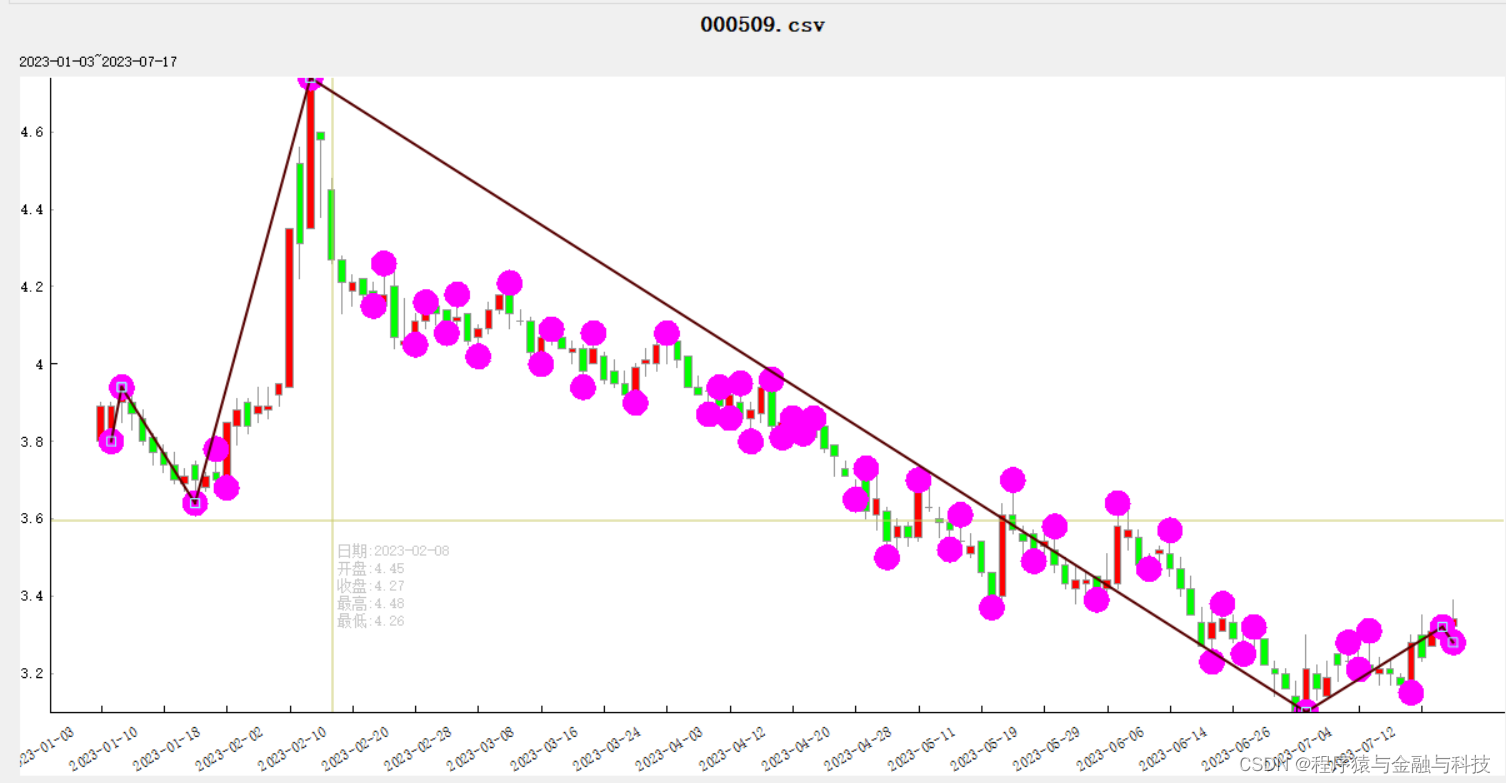
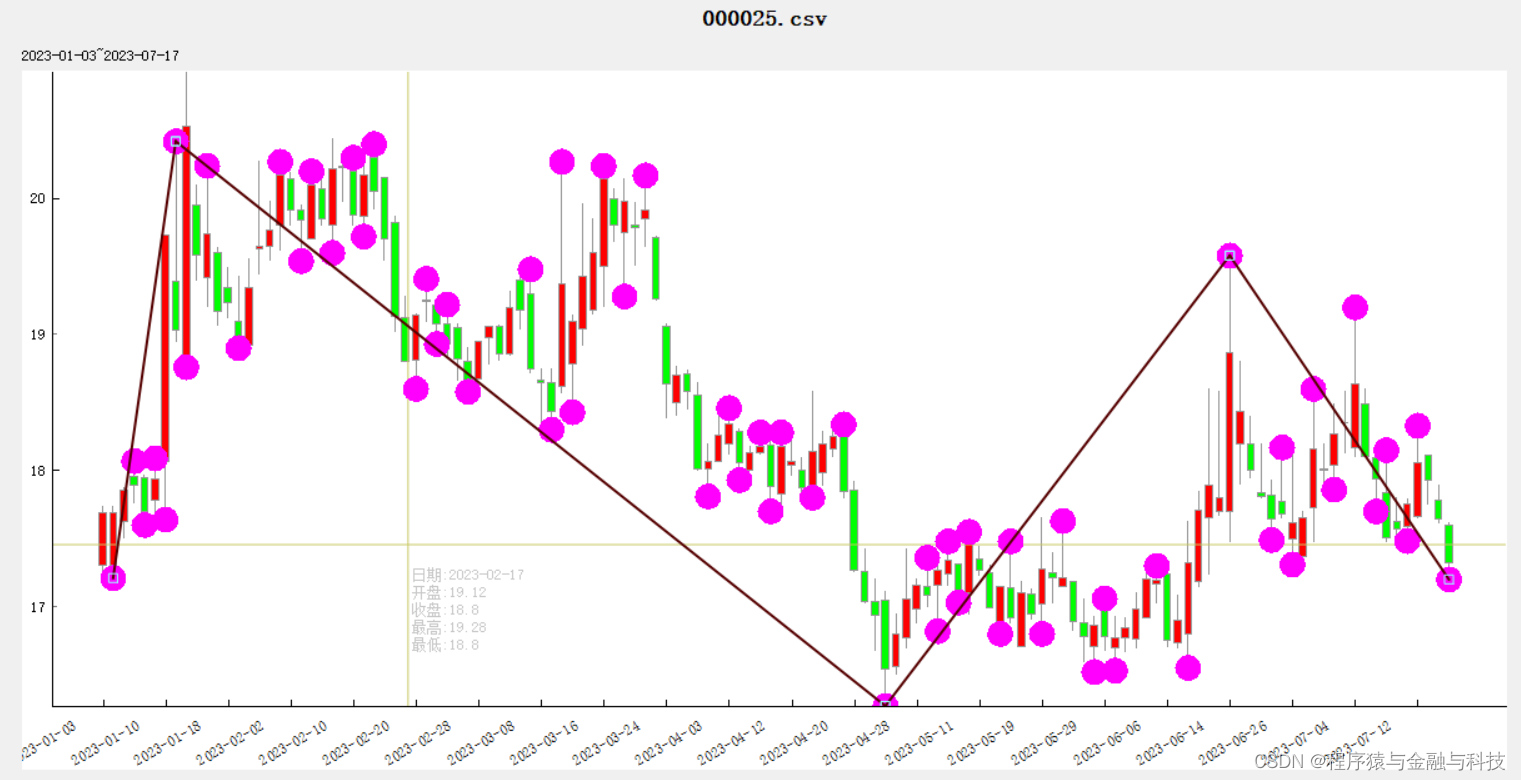
寻找方法
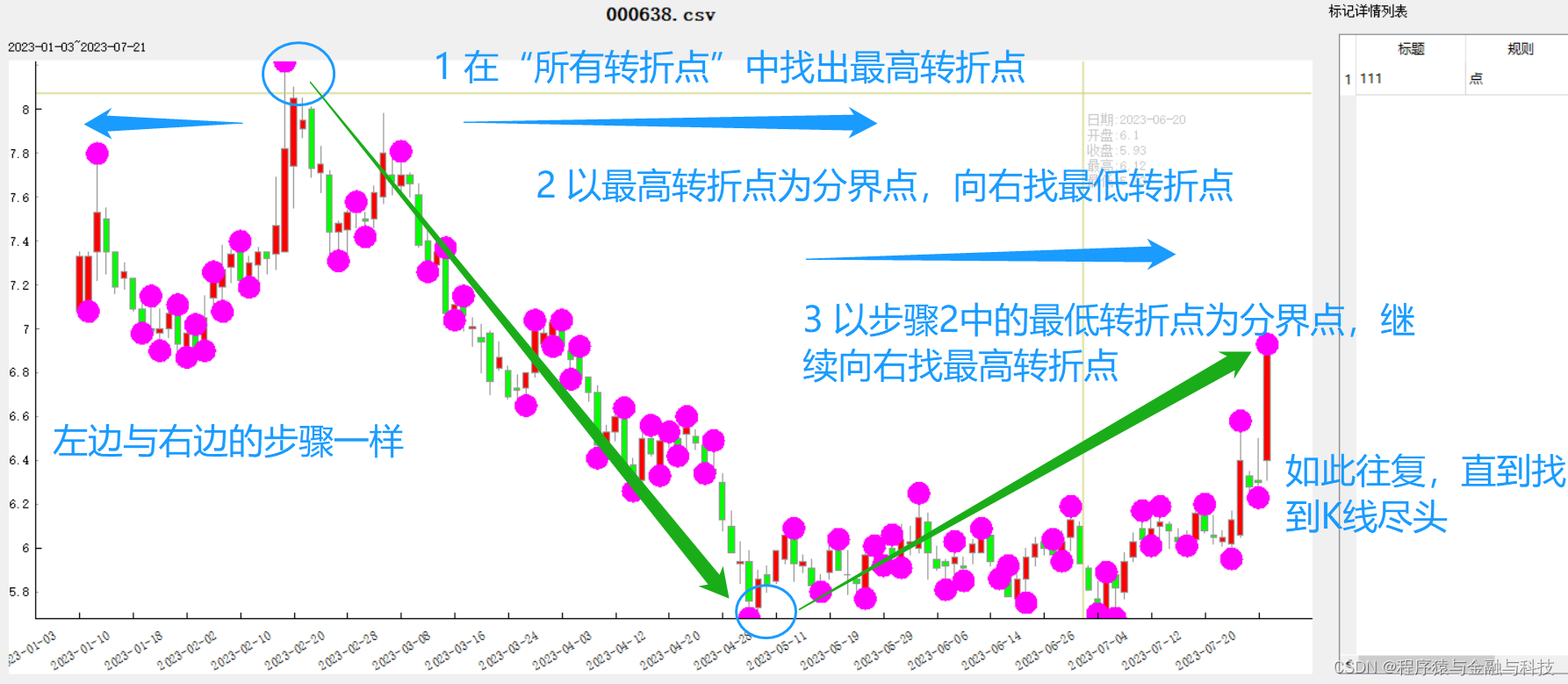
1 在所有转折点中找出最高转折点
2 以最高转折点为界线,向左向右寻找下一个转折点。向右寻找右边区域的最低转折点
3 以步骤2中找到的最低转折点为分界点,继续向右找最高转折点
4 。。。重复2、3步骤,直到寻找到K线的右边尽头
5 向左方向寻找与右边的逻辑一样
判断高低点连线是否有效
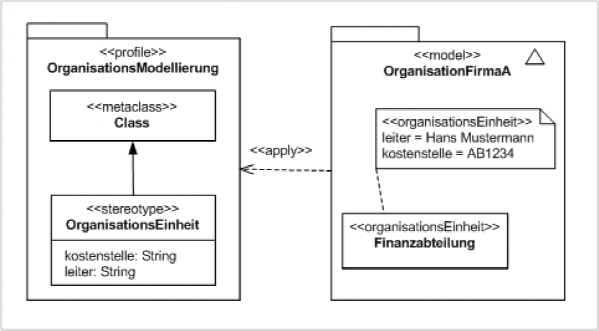
如果找到的高低点连线如下图,那么该高低点的连线就无效,需要再往里拆分高低点

所以,每次找到高低点,获得连线,需要有一个方法判断这个连线是否有效。
判断方法:
1 高低点连线,相当于一个一元一次方程 y=ax+b,得出这个方程的解
2 计算高低点区间所有转折点相对于高点低连线的分布,如果
1)大多数点都在线的附近,连线成立
2)大多数点都在线的一侧,连线成立
判断点相对连线位置的方法:
将点的x,y值代入一元一次方程
所有,ax+b-y > 0 的点在同一侧 ------------------------- (1)
所有,ax+b-y < 0 的点在同一侧 ------------------------- (2)
所有,|ax+b-y| 值很小的点,说明在连线附近 --------- (3)
分别计算 (1)(2)(3)占总体点数量的占比,从而得出所有点的分布情况
代码:
计算一元一次方程a b值方法
def caculate_a_b(x1,y1,x2,y2)->tuple:
a = (y2 - y1) / (x2 - x1)
b = y2 - a * x2
return a,b定位下一个转折点方法
def caculate_limit_point(pre_df,mark,contain_lr_yeah=True)->tuple:
if contain_lr_yeah:
df = pre_df.copy()
else:
df = pre_df.iloc[1:-1].copy()
# mark为True =>找最大值
if mark:
y = df['y'].max()
x = df.loc[df['y']==y].iloc[0]['x']
pass
else:
y = df['y'].min()
x = df.loc[df['y']==y].iloc[0]['x']
pass
return x,y
判断点相对连线位置方法
def check_point_location(pre_df,x0,y0,x1,y1):
# “大多数点”量化
one_size = 0.7
# “在线段附近”量化
near_line = 0.1
a,b = caculate_a_b(x0,y0,x1,y1)
if x0>x1:
df = pre_df.loc[(pre_df['x']>=x1) & (pre_df['x']<=x0)].copy()
else:
df = pre_df.loc[(pre_df['x']<=x1) & (pre_df['x']>=x0)].copy()
pass
df['ext'] = a*df['x']+b-df['y']
total_num = len(df)
bigger_num = len(df.loc[df['ext']>=0])
smaller_num = len(df.loc[df['ext']<=0])
if float(bigger_num/total_num)>=one_size or float(smaller_num/total_num)>=one_size:
return True
else:
# 是否大多数点都在线段附近
angle_line = math.fabs(df.iloc[0]['y']-df.iloc[-1]['y'])
df['ext00'] = df['ext'].abs()
df['ext01'] = df['ext00']/angle_line
ok_num = len(df.loc[df['ext01']<=near_line])
if float(ok_num/total_num)>=one_size:
return True
else:
# 刨除附件的点,远的点分布是否符合大多数在同一边
df['ext02'] = 0
df.loc[(df['ext01']>near_line) & (df['ext']>0),'ext02'] = 2
df.loc[(df['ext01']>near_line) & (df['ext']<0),'ext02'] = 3
bigger_num00 = len(df.loc[df['ext02']==2])
smaller_num00 = len(df.loc[df['ext02']==3])
total_num00 = bigger_num00 + smaller_num00
if float(bigger_num00 / total_num00) >= one_size or float(smaller_num00 / total_num00) >= one_size:
return True
else:
return False
pass
pass
向左右两个方向反复寻找方法
def find_band_by_max_min(pre_df,contain_lr_yeah=True):
final_list = []
waitting_list = []
df = pre_df.copy()
right_end_x = df.iloc[0]['x']
left_end_x = df.iloc[-1]['x']
# 找到最大值
first_x_max,first_y_max = caculate_limit_point(df,True,contain_lr_yeah)
# 向左开始找
left_x0 = first_x_max
left_y0 = first_y_max
left_mark = False
while True:
if left_x0 <= left_end_x:
break
pre_left_df = df.loc[df['x']<=left_x0].copy()
left_x1, left_y1 = caculate_limit_point(pre_left_df, left_mark)
# print('left',left_x0,left_y0,left_x1,left_y1)
res_left = check_point_location(pre_left_df,left_x0,left_y0,left_x1,left_y1)
if res_left:
final_list.append([[left_x0,left_y0],[left_x1,left_y1]])
left_x0 = left_x1
left_y0 = left_y1
left_mark = not left_mark
pass
else:
waitting_list.append([[left_x0, left_y0], [left_x1, left_y1]])
left_x0 = left_x1
left_y0 = left_y1
left_mark = not left_mark
pass
pass
# 向右开始找
right_x0 = first_x_max
right_y0 = first_y_max
right_mark = False
while True:
if right_x0 >= right_end_x:
break
pre_right_df = df.loc[df['x']>=right_x0].copy()
right_x1, right_y1 = caculate_limit_point(pre_right_df, right_mark)
# print('right',right_x0,right_y0,right_x1,right_y1)
res_right = check_point_location(pre_right_df, right_x0, right_y0, right_x1, right_y1)
if res_right:
final_list.append([[right_x0, right_y0], [right_x1, right_y1]])
right_x0 = right_x1
right_y0 = right_y1
right_mark = not right_mark
pass
else:
waitting_list.append([[right_x0, right_y0], [right_x1, right_y1]])
right_x0 = right_x1
right_y0 = right_y1
right_mark = not right_mark
pass
pass
return final_list,waitting_list主方法
def enter_main_two(pre_df):
df = pre_df.copy()
whole_final_list = []
whole_waitting_list = []
final_list,waiting_list = find_band_by_max_min(df)
whole_final_list.extend(final_list)
whole_waitting_list.extend(waiting_list)
if whole_waitting_list:
while True:
if not whole_waitting_list:
break
one_w = whole_waitting_list.pop()
x0 = one_w[0][0]
x1 = one_w[1][0]
if x0>x1:
w_df = df.loc[(df['x']>=x1) & (df['x']<=x0)].copy()
else:
w_df = df.loc[(df['x'] <= x1) & (df['x'] >= x0)].copy()
pass
one_final_list,one_waitting_list = find_band_by_max_min(w_df,False)
whole_final_list.extend(one_final_list)
whole_waitting_list.extend(one_waitting_list)
return whole_final_list运用并验证结果