文章目录
- 1. 二叉树的最近公共祖先
- 1.1 思路1(转换为链表相交问题)
- 1.2 链表相交问题讲解
- 1.3 思路2
- 1.4 思路2AC代码
- 2. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
- 2.1 思路分析
- 2.2 AC代码
- 3. 普通二叉树求最近公共祖先的优化-转化为路径相交的问题
- 3.1 思路分析
- 3.2 AC代码
1. 二叉树的最近公共祖先
题目链接: link
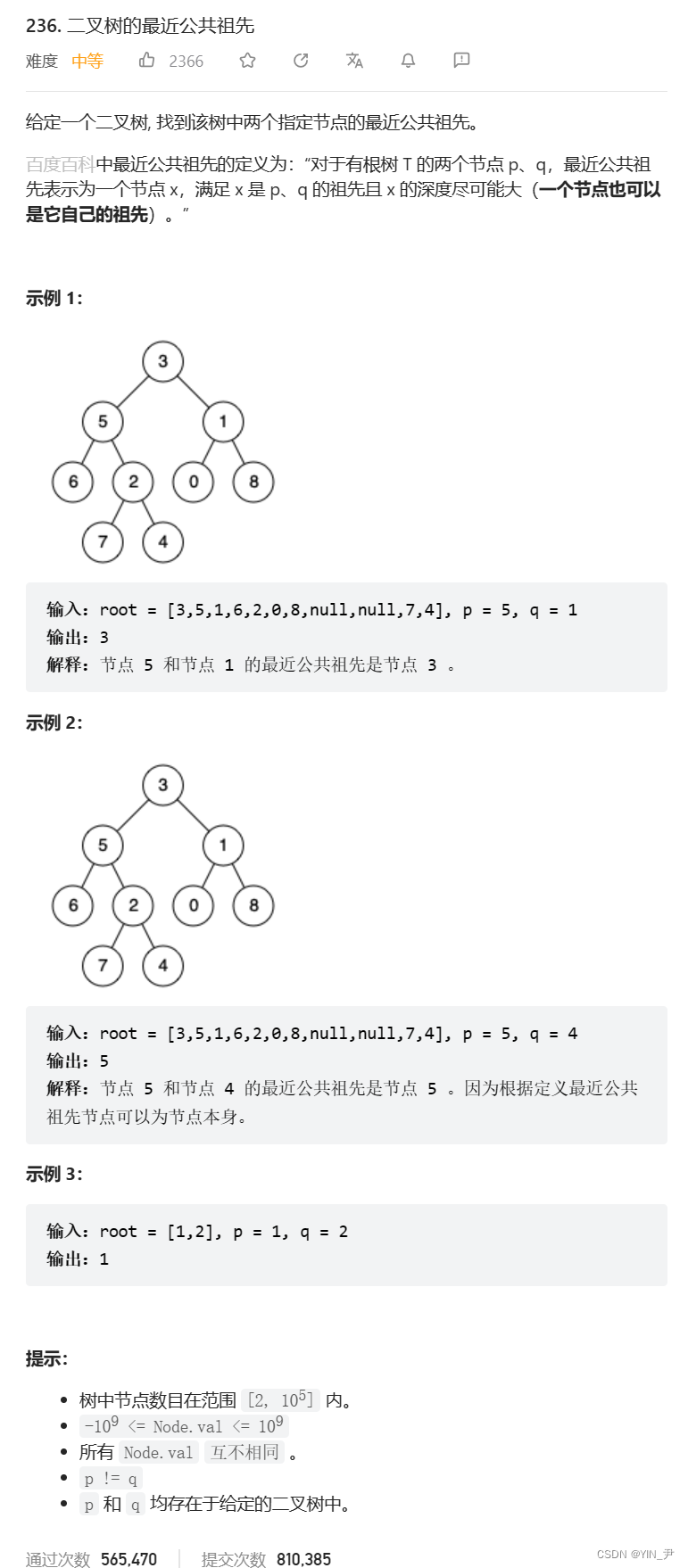
这道题呢,是给我们一棵二叉树,让我们找出两个指定结点的最近公共祖先。
首先我们来看一下,最近的公共祖先有哪几种情况:
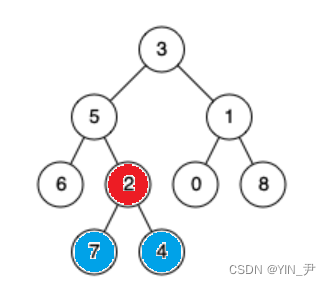
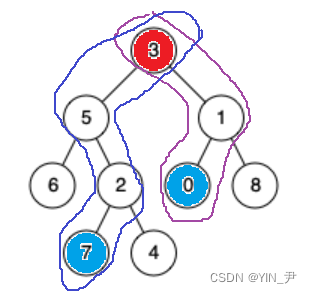
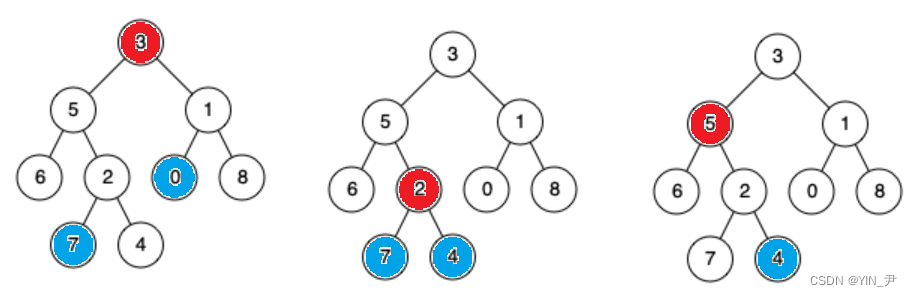
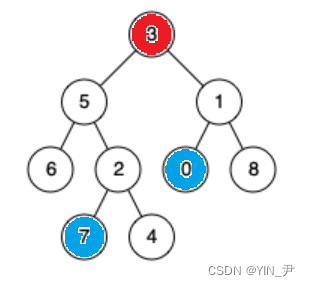
先来看这个,0和7的最近公共祖先是3,这个没什么问题
然后再看一个
7和4呢,2 、5 、3是不是都是它们两个的公共祖先啊,但是题目要求找最近的公共祖先,所以是2。
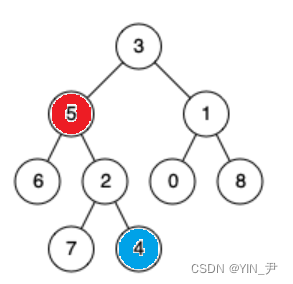
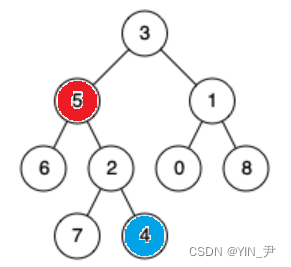
再看一种情况
5和4的公共祖先是谁啊?
我们可能会认为是3,但是题目说了,一个节点也可以是它自己的祖先,所以应该是5。
那了解了题目的意思,我们来分析一下解题思路。
ps:下面提供多种思路,但不会都实现出来代码,有些思路对于当前这道题目可能并不是特别可行,主要是帮助大家拓展思维。
1.1 思路1(转换为链表相交问题)
首先不知道大家有没有做过这样一道题:
就是链表那块有一个比较经典的题目——相交链表。
在leetcode上也有对应的题目
其实就是去找两个链表的第一个相交结点。
那大家看:
对于我们当前这道题,是找二叉树中两个结点的最近的公共祖先。
当前二叉树的结构只有左右孩子两个指针。
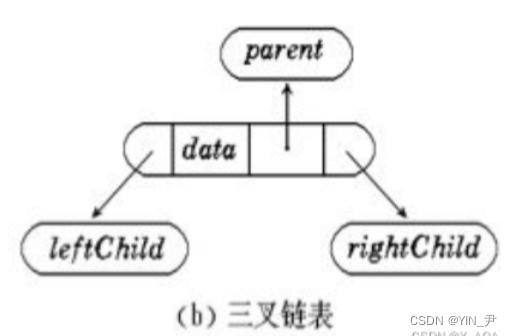
但如果它是一个三叉链的结构
即还有一个指向parent父结点的指针。
那这道题是不是就可以看作一个链表相交的问题了
因为有了parent指针我们就可以从孩子结点沿着parent往上走了,就像链表从前完后走一样。
1.2 链表相交问题讲解
那有做过链表相交问题的回顾一下,没做过的思考一下,链表相交问题,可以怎么去找第一个交点
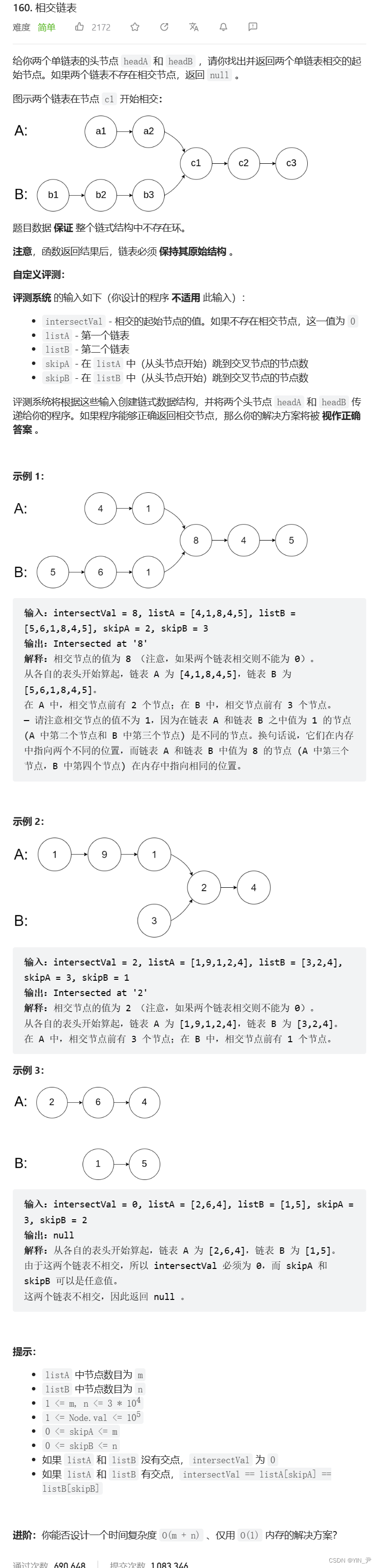
那在这里我提供两种思路。
第一种,暴力求解:
让A链表的中每个结点依次与B中所有结点逐个比较,第一个相同的结点就是第一个交点。
//暴力求解,让A链表的每个结点依次与B中所有结点逐个比较。O(N^2)
struct ListNode* getIntersectionNode(struct ListNode* headA, struct ListNode* headB)
{
struct ListNode* curA = headA;
struct ListNode* curB = headB;
while (curA)
{
curB=headB;
while (curB)
{
if (curA == curB)
return curA;
curB = curB->next;
}
curA = curA->next;
}
return NULL;
}
ps:我这里给的代码是之前用C语言写的。
那想要效率高一点,第二种解法:
首先遍历两个链表找尾,判断两个链表的尾结点是否相同,不相同,那就肯定不相交,直接返回false。
如果相交的话,去找相交点,怎么找呢?
计算出两个链表长度的差值gap,然后让长的那个链表先走gap步,然后两个链表一块走,每走一步,判断两个结点是否相同,第一个相同的结点就是第一个交点。
#include <math.h>
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
struct ListNode *curA=headA;
struct ListNode *curB=headB;
int lenA=0;
int lenB=0;
//找尾,先判断是否相交,不相交直接返回NULL,相交再找
while(curA->next)
{
lenA++;
curA=curA->next;
}
//计算准确长度应该这样写:while(curA)
//这样while(curA->next)比实际长度小1,但是两个都小1,不影响差值
//而这样写循环结束cur就是尾,可直接判断是否相交
while(curB->next)
{
lenB++;
curB=curB->next;
}
//尾不相等,则不相交
if(curA!=curB)
return NULL;
//计算差值
int gap=abs(lenA-lenB);
//找出长的那一个
struct ListNode *longlist=headA;
struct ListNode *shortlist=headB;
if(lenB>lenA)
{
longlist=headB;
shortlist=headA;
}
//长表先走差值步
while(gap--)
{
longlist=longlist->next;
}
//再一起走,比较两个链表的当前结点是否相同
//,第一个相同的就是第一个交点
while(longlist!=shortlist)
{
longlist=longlist->next;
shortlist=shortlist->next;
}
return longlist;
}
但是现在题目中的二叉树并不是三叉链结构,要想拷贝转换成三叉链也比较麻烦。
所以我们看第二种思路:
1.3 思路2
那我们要直接去找,怎么做呢?
其实还可以考虑用递归。
观察上面我们分析的这三种情况:
会发现
第一种情况,要查找的两个结点一个在整棵树根结点的左子树上,一个在右子树上,所以根结点就是它们最近的公共祖先。
第二种情况的话,两个结点都在根结点的左子树(如何判断在哪个子树上,就需要我们自己写一个类似find的函数判断),那首先根结点不会是最近的公共祖先了,其次,公共结点有可能在右子树吗?
是绝对不可能的,所以我们就可以递归去左子树查找。
那后续也是一样,到了左子树发现两个结点都在右子树上,所以再递归到右子树查找。
那此时就走到了2的位置
那一个结点在2的左,一个在2的右,所以2就是最近的公共祖先,就找到了。
那第三种情况呢?
那对于第三种情况首先还是会递归到左子树,然后走到5这个结点,会发现一个结点时5本身,另一个结点在5的右子树。
所以5就是最近公共祖先。
因此我们得出一个结论,如果两个结点里面有一个是某棵树的根结点,另一个在这棵树的子树上,那么这个根结点就是最近公共祖先。
1.4 思路2AC代码
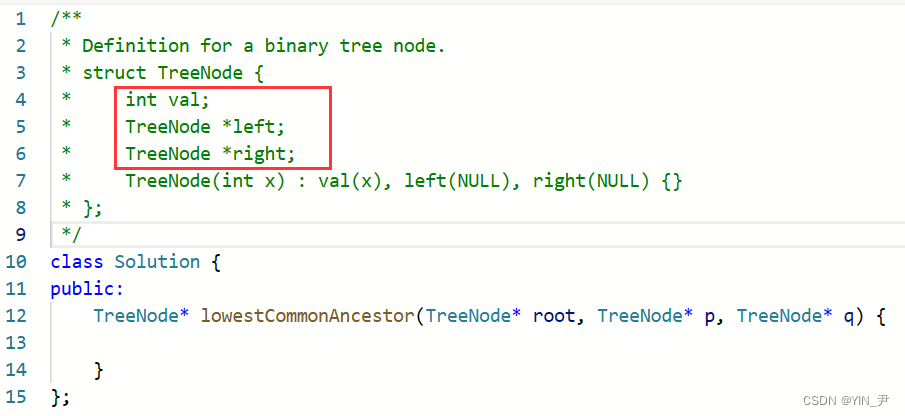
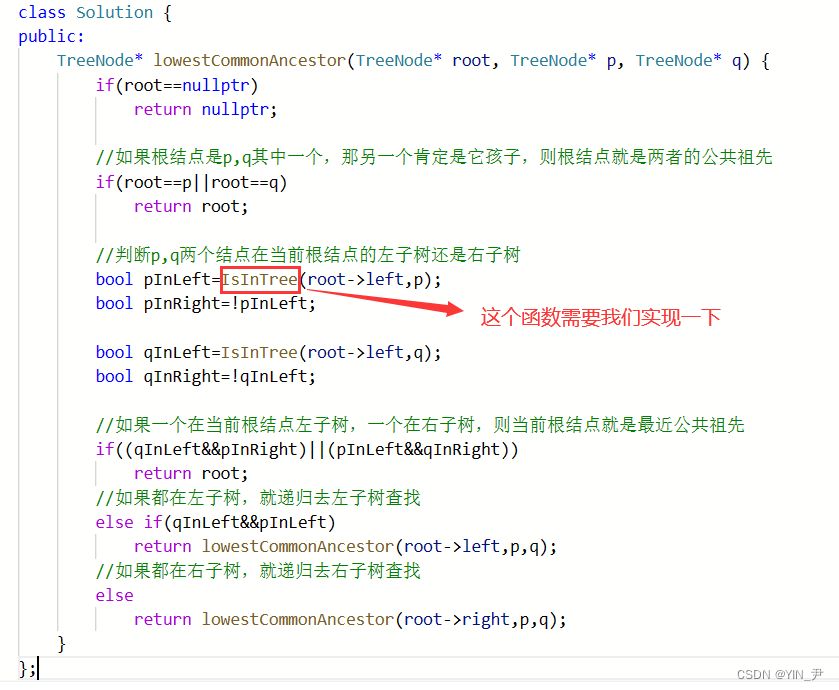
那我们来写一下代码:
那然后我们要来实现一下判断一个结点在左子树还是在右子树的这个IsInTree函数。
那我们就写完了
class Solution {
public:
bool IsInTree(TreeNode* root, TreeNode* x)
{
if(root==nullptr)
return false;
return root==x
|| IsInTree(root->left,x)
|| IsInTree(root->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr)
return nullptr;
//如果根结点是p,q其中一个,那另一个肯定是它孩子,则根结点就是两者的公共祖先
if(root==p||root==q)
return root;
//判断p,q两个结点在当前根结点的左子树还是右子树
bool pInLeft=IsInTree(root->left,p);
bool pInRight=!pInLeft;
bool qInLeft=IsInTree(root->left,q);
bool qInRight=!qInLeft;
//如果一个在当前根结点左子树,一个在右子树,则当前根结点就是最近公共祖先
if((qInLeft&&pInRight)||(pInLeft&&qInRight))
return root;
//如果都在左子树,就递归去左子树查找
else if(qInLeft&&pInLeft)
return lowestCommonAncestor(root->left,p,q);
//如果都在右子树,就递归去右子树查找
else
return lowestCommonAncestor(root->right,p,q);
}
};
测试一下
但是我们看到这种方法其实时间效率是比较低的,它的时间复杂度是一个O(N^2)
首先我们从根节点不断往左右子树去递归的过程是一个O(N),然后每一次递归去判断在不在的过程也是一个O(N),所以是O(N^2)
不过不用担心,后面我们会进行优化。
2. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
那我们上面讲的是普通二叉树寻找公共最近祖先的问题,那这道题其实也有搜索二叉树的版本
题目链接: link
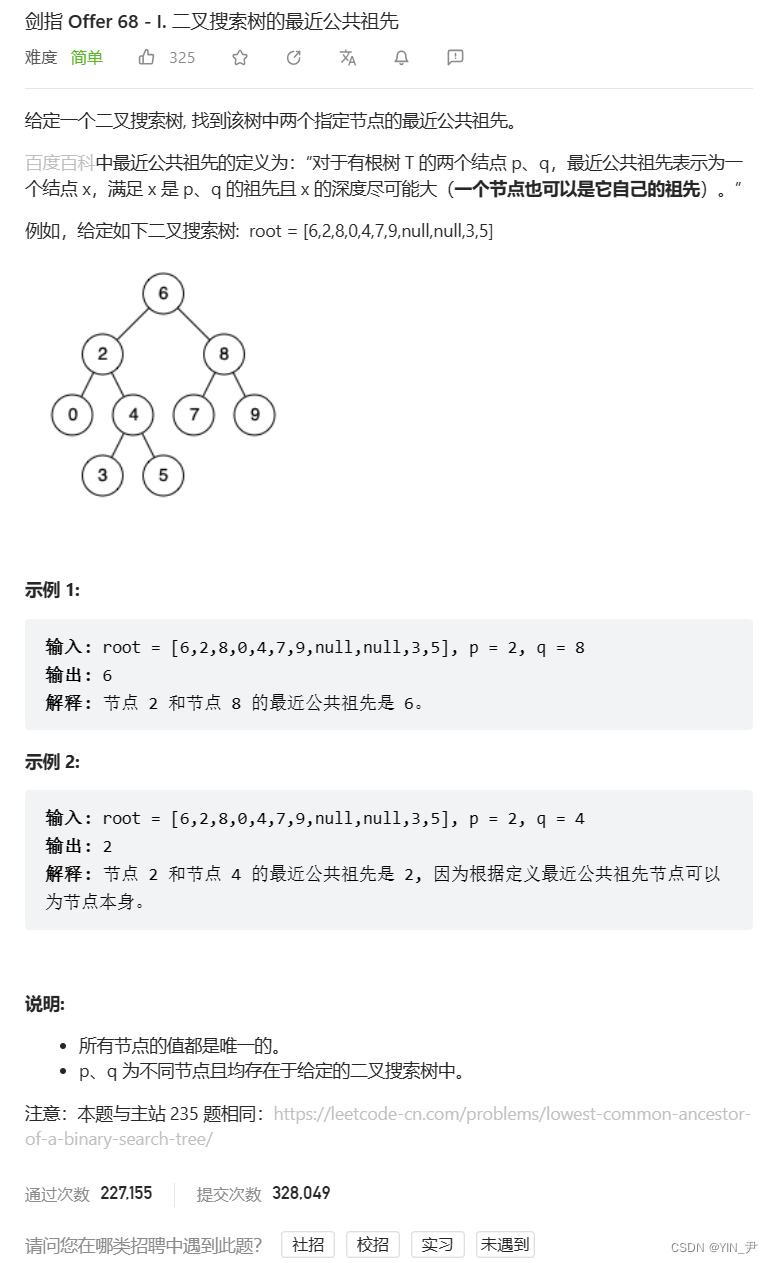
题目没什么变化,就是上一题是普通二叉树,这道题是搜索二叉树
2.1 思路分析
其实思路根上一题的思路还是一样的,但是,对于搜索二叉树来说,我们还需要手动写一个函数去判断结点在左子树还是在右子树吗?
🆗,不需要了,因为我们通过它们与根结点的大小关系就直接可以判断出来了。
那这样同样的思路,时间复杂度其实就变成O(N)了。
因为不再需要使用那个函数(O(N))去判断了
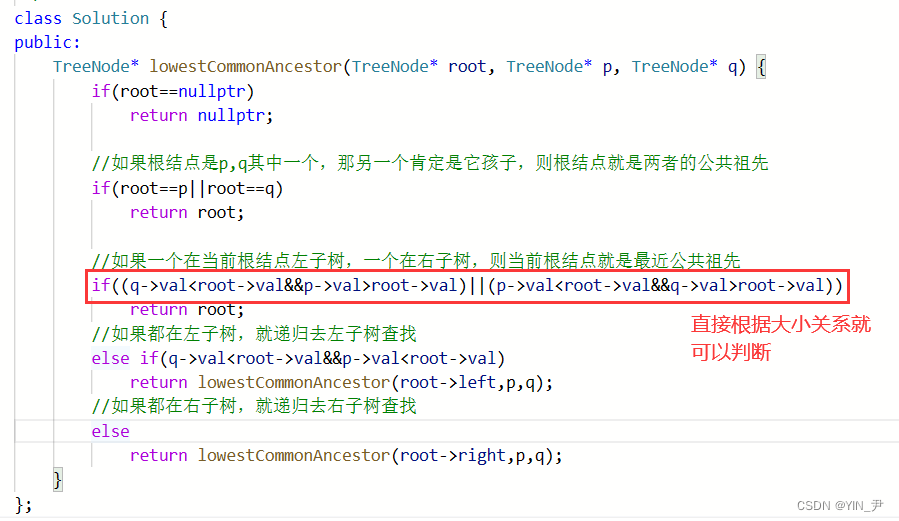
2.2 AC代码
那代码也很简单,把上一题那个拷贝过来,简单修改一下就行了
这次的效率明显就高了。
3. 普通二叉树求最近公共祖先的优化-转化为路径相交的问题
上面普通二叉树求最近公共祖先的问题
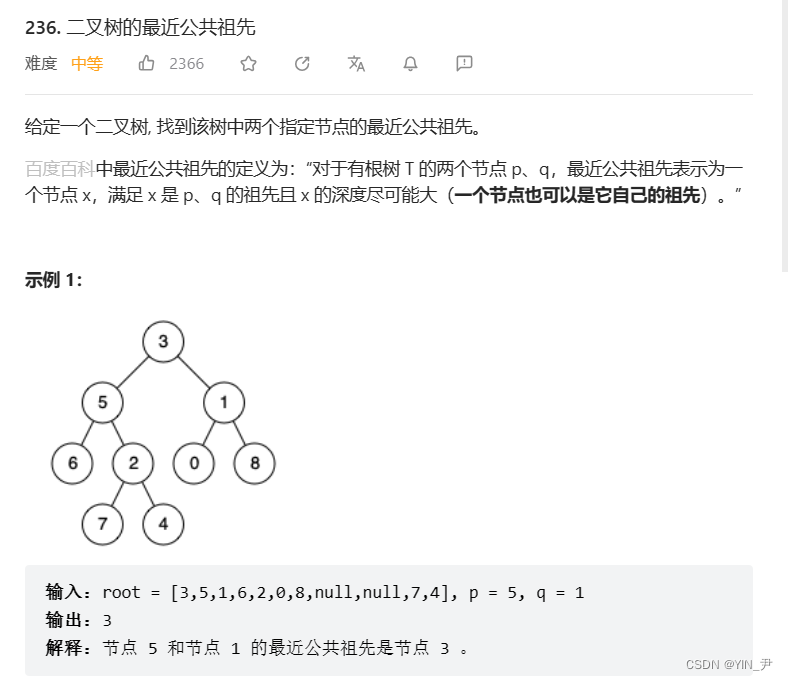
我们实现的算法效率比较低,是O(N^2)的。
那能不能进行一个优化呢?
我们可以将它转换成一个路径相交问题,转换之后的解法就类似上面提到的链表相交问题。
3.1 思路分析
那具体怎么做呢?
首先我们可以获取从根结点开始到两个结点的路径,然后保存到容器里面:
那选择什么容器保存路径呢?
这里用栈(stack)是比较合适的(先进后出),后面大家就会明白。
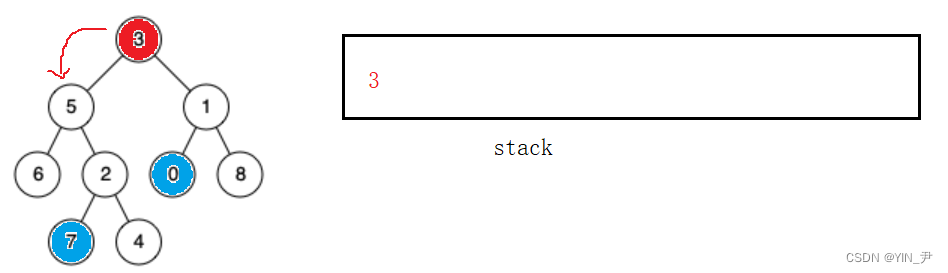
我们走一个前序的DFS来获取路径:
以这张图为例
从根结点开始,首先判断根结点不为空,为空直接返回false,不为空先把根结点入栈,然后判读根结点是不是目标结点,是的话,直接返回true,栈里面的根结点就是路径,不是的话,就去左子树找。
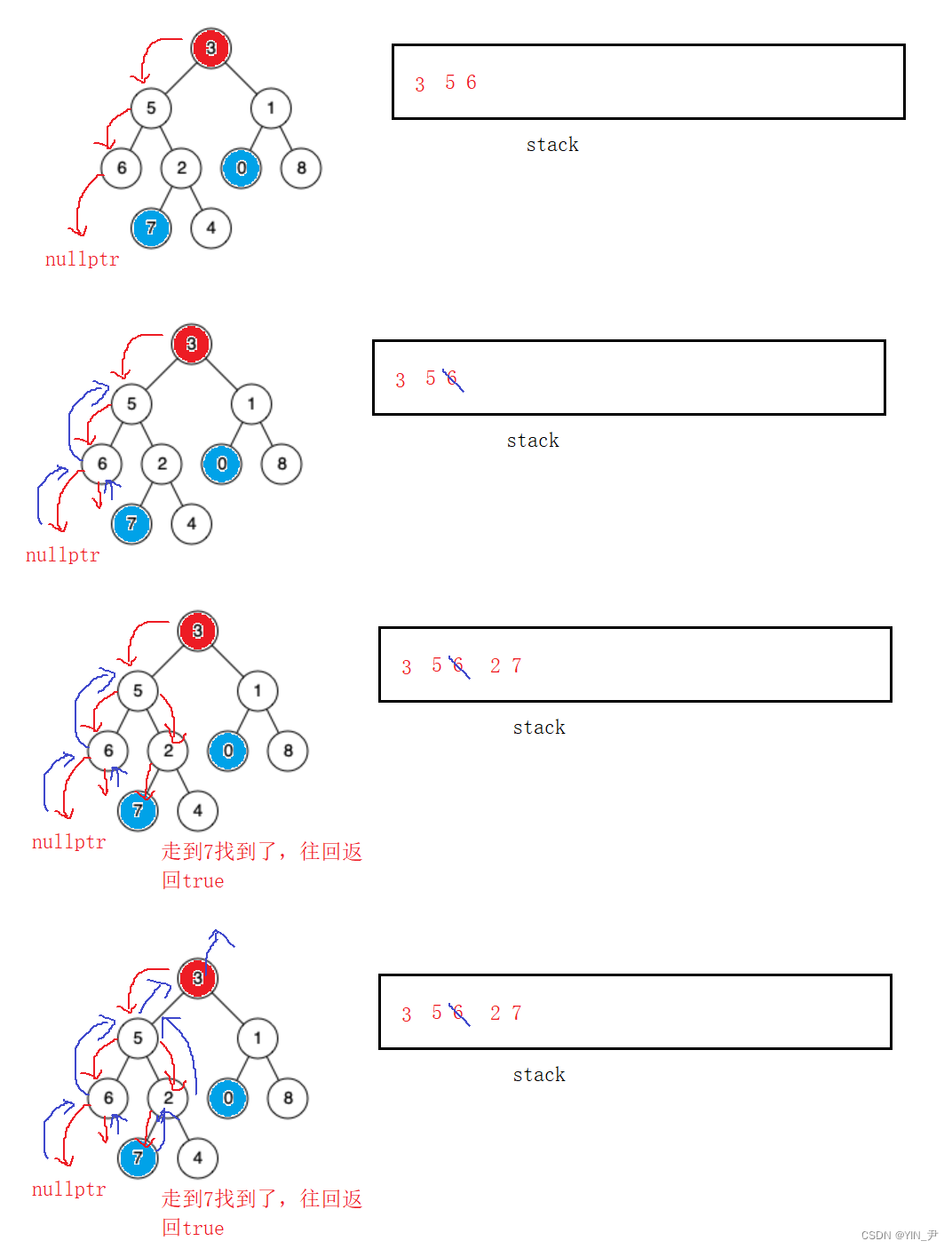
递归去左子树继续找(还是一样,先看根结点为不为空,不为空入栈,判断是否是目标结点,不是就去它的左右子树接着找),如果左子树找到了,就返回true,左子树没找到,再去右子树去找右子树找到了,就返回true。
如果左右子树都没找到,说明走当前这个结点时不正确的路径,那就需要把它从栈里面pop掉。
然后,返回flase,返回到上一层递归调用的地方,继续去上一层,没有找过的地方找。
那大家看这个找路径这个算法,时间复杂度是多少?
是不是O(N)啊。
那获取了路径,后的步骤就跟链表相交找交点类似:
先让元素多的那个栈出元素,出到两个栈元素个数一样的时候,同时出,然后遇到第一个相同的元素,就是最近的公共祖先。
那这也是一个O(N)
所以该算法整体就是一个O(N)的算法。
当然这种思路的代价是空间复杂度会高一点,因为我们额外开了两个栈。
3.2 AC代码
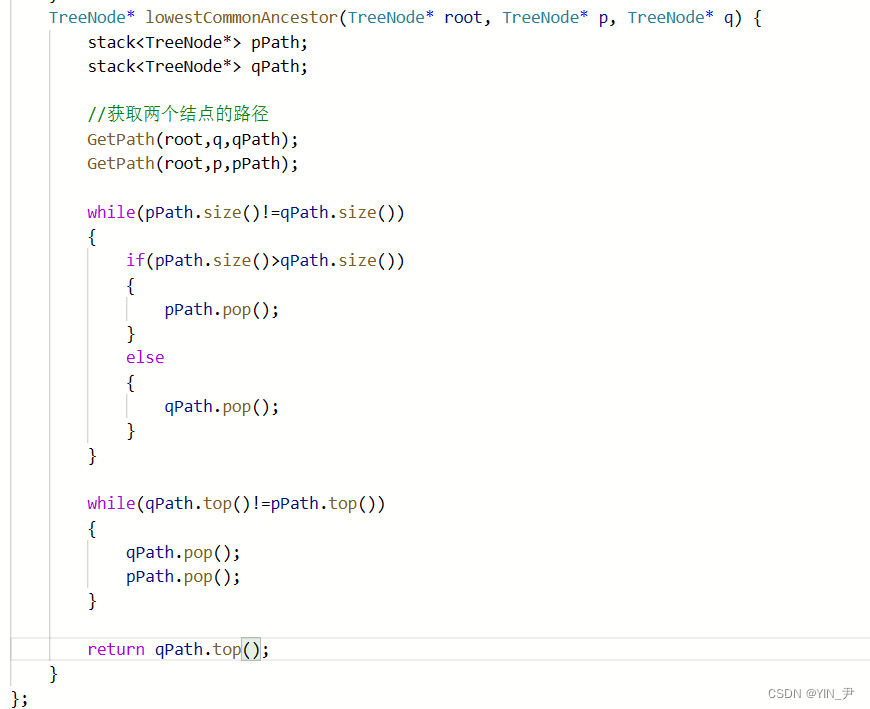
我们来写一下代码:
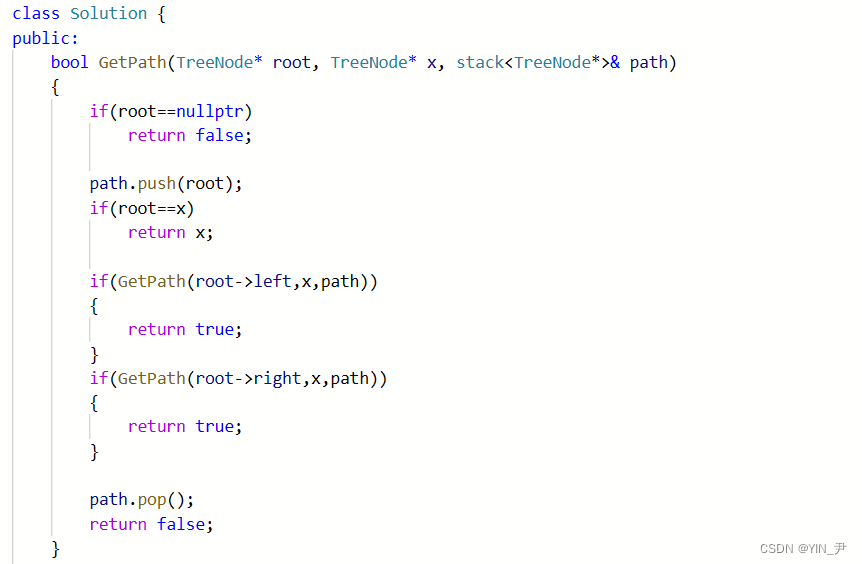
然后我们写一下获取路径的函数就行了。
提交一下:
比之前的还是快了挺多的。
class Solution {
public:
bool GetPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
{
if(root==nullptr)
return false;
path.push(root);
if(root==x)
return x;
if(GetPath(root->left,x,path))
{
return true;
}
if(GetPath(root->right,x,path))
{
return true;
}
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath;
stack<TreeNode*> qPath;
//获取两个结点的路径
GetPath(root,q,qPath);
GetPath(root,p,pPath);
while(pPath.size()!=qPath.size())
{
if(pPath.size()>qPath.size())
{
pPath.pop();
}
else
{
qPath.pop();
}
}
while(qPath.top()!=pPath.top())
{
qPath.pop();
pPath.pop();
}
return qPath.top();
}
};