目录
- 第四章:串
- 4.1串的定义和实现
- 4.1.1串的定义
- 4.1.2串的基本操作
- 字符集编码
- 4.1.3串的存储结构
- 1. 定长顺序存储表示
- 基本操作实现(基于方案四)
- 2. 堆分配存储表示
- 3. 串的链式存储
- 结合链表思考优缺点
- 知识回顾
- 4.2串的模式匹配
- 4.2.1朴素模式匹配算法
- 时间复杂度分析:
- 4.2.2改进的模式匹配算法——KMP算法
- 1. 求next数组
- 2. 利用next数组进行模式匹配
- 3. 时间复杂度分析
- 4.2.3 next数组的优化思路nextval,优化KMP
第四章:串
4.1串的定义和实现
4.1.1串的定义
-
串: 零个或多个字符组成的有限序列,如 S = ‘iPhone 11 Pro Max?’;
-

-
串名:S是串名;
-
串的长度:串中字符的个数n;
-
空串:n=0时的串;
-
子串:串中任意多个连续的字符组成的子序列称为该串的子串;
-
主串:包含子串的串;
-
字符在主串中的位置:某个字符在串中的序号(从1开始);
-
子串在主串中的位置:子串的第一个字符在主串中的位置;
空串 V.S 空格串:
- M = ‘’ 是空串;
- N = ’ ’ 是空格串;
串 V.S 线性表:
- 串是特殊的线性表,数据元素之间呈线性关系(逻辑结构相似);
- 串的数据对象限定为字符集:中文字符、英文字符、数字字符、标点字符…
- 串的基本操作,如增删改除通常以子串为操作对象
4.1.2串的基本操作

StrCompare(S, T) 串的比较操作,参照英文词典排序方式;若S > T,返回值>0; S = T,返回值=0 (需要两个串完全相同) ; S < T,返回值<0;
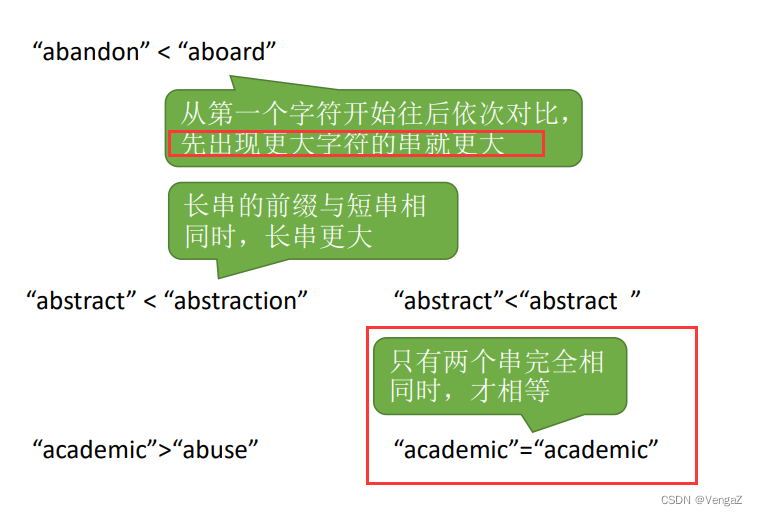
字符集编码
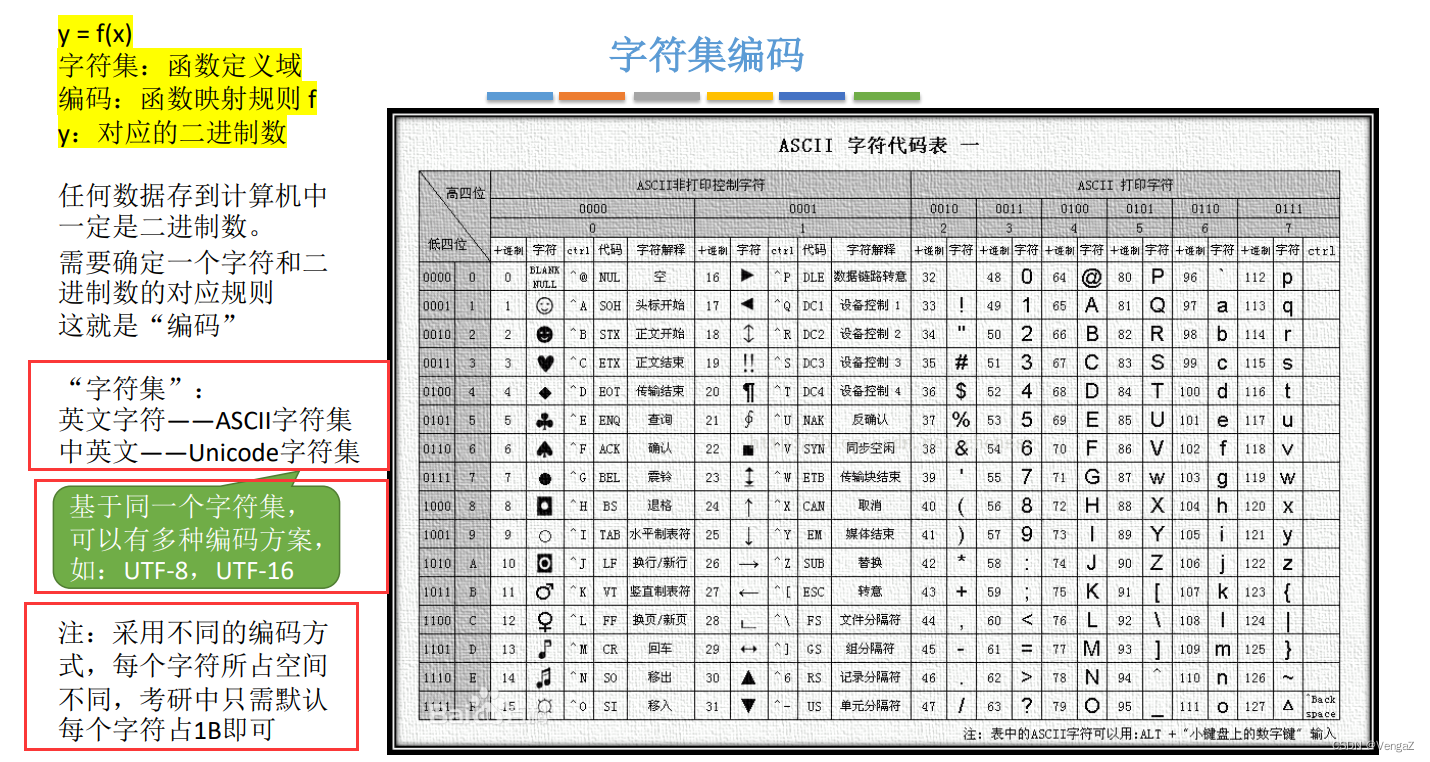
4.1.3串的存储结构
1. 定长顺序存储表示
#define MAXLEN 255 //预定义最大串长为255
typedef struct{
char ch[MAXLEN]; //静态数组实现(定长顺序存储)
//每个分量存储一个字符
//每个char字符占1B
int length; //串的实际长度
}SString;
串长的两种表示法:
-
方案一:用一个额外的变量length来存放串的长度(保留ch[0]);
-
方案二:用ch[0]充当length;
优点:字符的位序和数组下标相同;
缺点: 字符串长度0-2^8-1 -
方案三:没有length变量,以字符’\0’表示结尾(对应ASCII码的0);
缺点:需要从头到尾遍历; -
方案四——最终使用方案:ch[0]废弃不用,声明int型变量length来存放串的长度(方案一与方案二的结合)
基本操作实现(基于方案四)
#define MAXLEN 255
typedef struct{
char ch[MAXLEN];
int length;
}SString;
// 1. 求子串
bool SubString(SString &Sub, SString S, int pos, int len){
//子串范围越界
if (pos+len-1 > S.length) //pos+len-1是因为这样子是最后一个元素的位置
return false; //如下边的i<pos+len,就是i最大值是pos+len-1
for (int i=pos; i<pos+len; i++)
Sub.cn[i-pos+1] = S.ch[i];
Sub.length = len;
return true;
}
// 2. 比较两个串的大小
int StrCompare(SString S, SString T){
for (int i; i<S.length && i<T.length; i++){
if(S.ch[i] != T.ch[i])
return S.ch[i] - T.ch[i];
}
//扫描过的所有字符都相同,则长度长的串更大
return S.length - T.length;
}
// 3. 定位操作
int Index(SString S, SString T){
int i=1;
n = StrLength(S);
m = StrLength(T);
SString sub; //用于暂存子串
while(i<=n-m+1){ //n-m+1是最后一个能取到长m的字串的位置,所以可以等于
SubString(Sub,S,i,m);
if(StrCompare(Sub,T)!=0)
++i;
else
return i; // 返回子串在主串中的位置
}
return 0; //S中不存在与T相等的子串
}
2. 堆分配存储表示
堆存储结构的特点:仍以一组空间足够大的、地址连续的存储单元依次存放字符序列,但它们的存储空间是在程序执行过程种动态分配的 。
通常,C语言提供的串类型就是以这种存储方式实现的。由动态分配函数malloc()分配一块实际串长所需要的存储空间(“堆”),如果分配成功,则返回此空间的起始地址,作为串的基址。由free()释放串不再需要的空间
堆存储结构的优点:堆存储结构既有顺序存储结构的特点,处理(随机取子串)方便,操作中对串长又没有任何限制,更显灵活,因此在串处理的应用程序中常被采用。
//动态数组实现
typedef struct{
char *ch; //按串长分配存储区,ch指向串的基地址
int length; //串的长度
}HString;
HString S;
S.ch = (char *) malloc(MAXLINE * sizeof(char)); //基地址指针指向连续空间的起始位置
//malloc()需要手动free()
S.length;
3. 串的链式存储
typedef struct StringNode{
char ch; //每个结点存1个字符
struct StringNode *next;
}StringNode, * String;
问题:存储密度低,每个字符1B,每个指针4B(32位的机器上);
解决方案:每一个链表的结点存储多个字符——每个结点称为块——块链结构
typedef struct StringNode{
char ch[4]; //每个结点存多个个字符
struct StringNode *next;
}StringNode, * String;
结合链表思考优缺点
- 存储分配角度:链式存储的字符串无需占用连续空间,存储空间分配更灵活;
- 操作角度:若要在字符串中插入或删除某些字符,则顺序存储方式需要移动大量字符,而链式存储不用;
- 若要按位序查找字符,则顺序存储支持随机访问,而链式存储只支持顺序访;
知识回顾
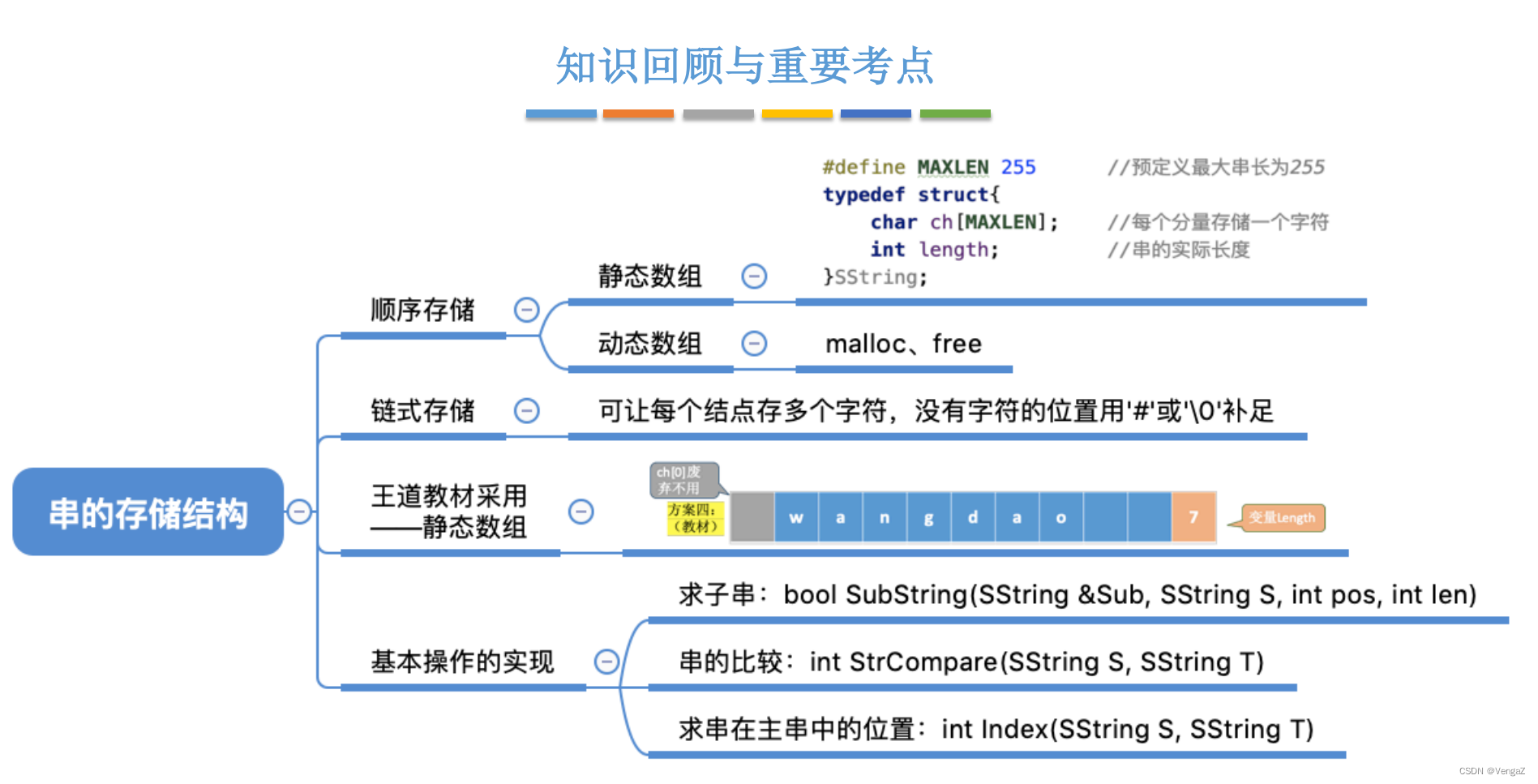
4.2串的模式匹配
模式匹配:子串的定位操作称为串的模式,它求的是子串(常称模式串)在主串中的位置。

4.2.1朴素模式匹配算法
n-m+1主串中能有的串个数
int Index(SString S, SString T){
int i=1; //扫描主串S
int j=1; //扫描模式串T
while(i<=S.length && j<=T.length){
if(S.ch[i] == T.ch[j]){
++i;
++j; //继续比较后继字符
}
else{
i = i-j+2; //回到这次匹配的第一个位置之前+1得到匹配的第一个位置
//再+1才能得到下一次匹配的第一个位置
j=1; //指针后退重新开始匹配
}
}
if(j>T.length) //匹配成功,返回第一个字符位置
return i-T.length;
else
return 0;
}
时间复杂度分析:
主串长度为n,模式串长度为m
最多比较n-m+1个子串
- 最坏时间复杂度 = O(nm)
每个子串都要对比m个字符(对比到最后一个字符才匹配不上),共要对比n-m+1个子串,复杂度 = O((n-m+1)m) = O(nm - m^2 + m) = O(nm)
PS:大多数时候,n>>m - 比较好时间复杂度 = O(n)
每个子串的第一个字符就匹配失败,共要对比n-m+1个子串,复杂度 = O(n-m+1) = O(n)
匹配一次就匹配成功:O(m)
4.2.2改进的模式匹配算法——KMP算法
不匹配的字符之前,一定是和模式串一致的;
根据模式串T,求出next数组(只与模式串有关,与主串无关),利用next数组进行匹配,当匹配失败时,主串的指针 i 不再回溯!
next数组是根据子串求出来的,当前面的字符串已知时如果有重复的,从当前的字符匹配即可。
1. 求next数组
- 作用:当模式串的第j个字符失配时,从模式串的第next[j]继续往后匹配;
- 对于任何模式串,当第1个字符不匹配时,只能匹配下一个子串,因此,next[1] = 0——表示模式串应右移一位,主串当前指针后移一位,再和模式串的第一字符进行比较;
- 对于任何模式串,当第2个字符不匹配时,应尝试匹配模式串的第一个字符,因此,next[2] = 1;

分界线后的第一个元素的位序就是next[j]的值
2. 利用next数组进行模式匹配
int Index_KMP(SString S, SString T, int next[]){
int i=1; //主串
int j=1; //模式串
while(i<S.length && j<=T.length){
if(j==0 || S.ch[i]==T.ch[j]){ //第一个元素匹配失败时
++j;
++i; //继续比较后继字符
}
else
j=next[j] //模式串向右移动
}
if(j>T.length)
return i-T.length; //匹配成功
}
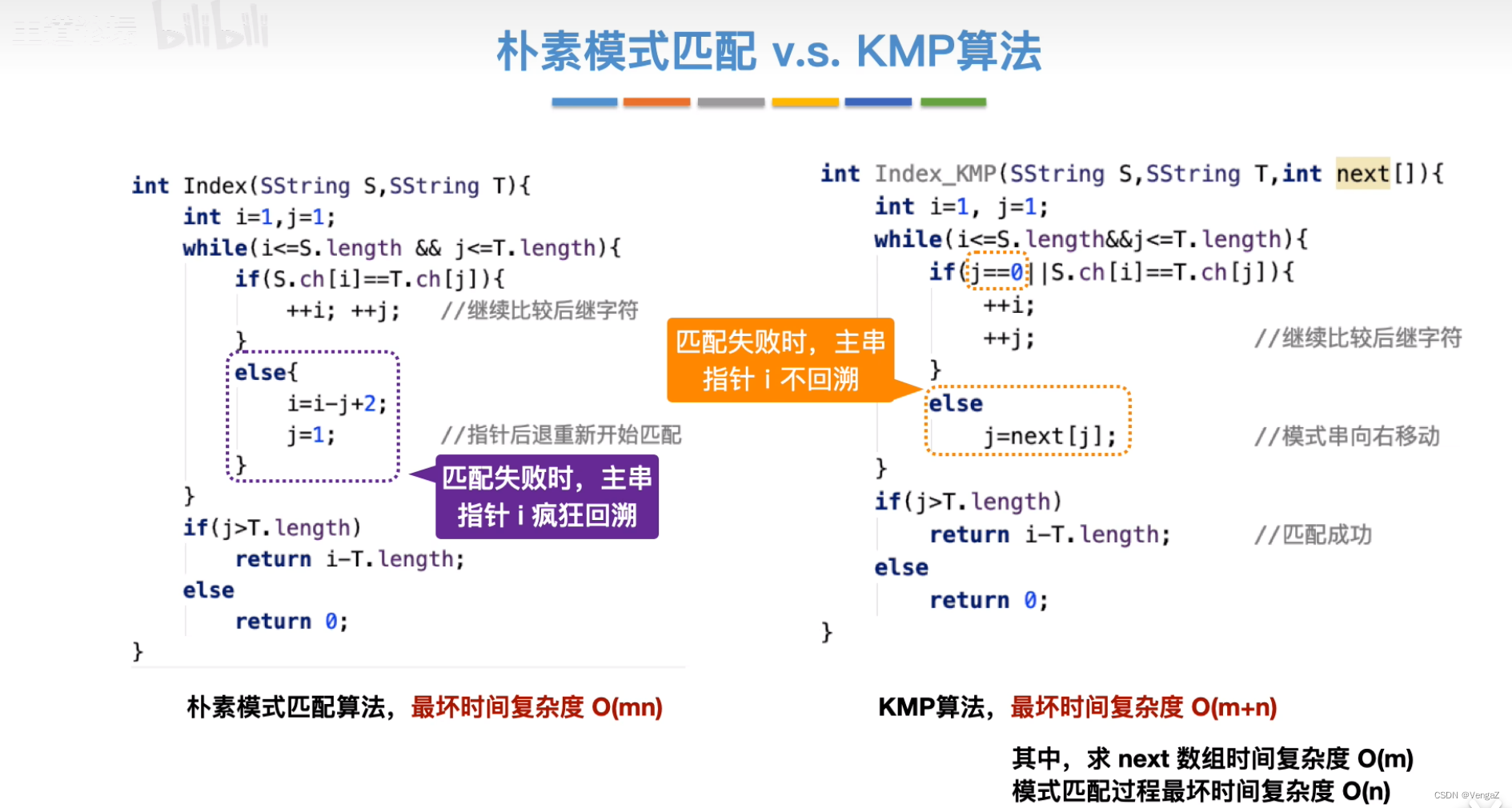
3. 时间复杂度分析
- 求next数组时间复杂度 = O(m)
- 模式匹配过程最坏时间复杂度 = O(n)
- KMP算法的最坏时间复杂度 = O(m+n)
4.2.3 next数组的优化思路nextval,优化KMP

如果next[j]的值对应的模式串的值相等,则说明就算跳转到这个位置也一样匹配失败,所以nextval[j]的值就是next[j]的值减一,再判断还会不会一样。