文章目录

聚类
- K-means 聚类
- - 1 准备数据
  - 2 给定聚类中心，计算每个点属于哪个聚类，定义函数实现
  - 3 根据已有的数据的标记，来重新更新聚类中心，定义相应的函数
  - 4 初始化聚类中心，定义相应的函数
  - 5 定义K-means算法
  - 6 绘制各个聚类的图
  - 7 定义评价函数--即任意一点所在聚类与聚类中心的距离平方和
  - 8 使用“肘部法则”选取k值
  - 9 画张图来可视化选择K
  - 10 对任意样本来预测其所属的聚类
- 试试Sklearn
- 实验1 K-means实现无监督聚类
- - 1 定义和调用更新每个样本所属聚类，聚类中心更新，初始化聚类中心的参数
  - 2 定义Kmeans算法获得最终的聚类中心和样本所属聚类索引
  - 3 绘制各个聚类的图
  - 4 定义评价函数--即任意一点所在聚类与聚类中心的距离平方和
  - 5 使用“肘部法则”选取k值
  - 6 对任意样本来预测其所属的聚类
  - 7 试试SKLERAN

聚类

在本练习中，我们将实现K-means聚类

K-means 聚类

我们将实施和应用K-means到一个简单的二维数据集，以获得一些直观的工作原理。 K-means是一个迭代的，无监督的聚类算法，将类似的实例组合成簇。该算法通过猜测每个簇的初始聚类中心开始，然后重复将实例分配给最近的簇，并重新计算该簇的聚类中心。我们要实现的第一部分是找到数据中每个实例最接近的聚类中心的函数。

1 准备数据

无监督学习中，数据是不带任何标签的

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import pandas as pd
import numpy as np
data=pd.read_csv("data/ex7data2.csv")
data.head()

	X1	X2
0	1.842080	4.607572
1	5.658583	4.799964
2	6.352579	3.290854
3	2.904017	4.612204
4	3.231979	4.939894

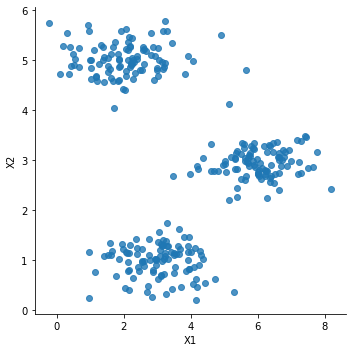
import seaborn as sb
plt.figure(figsize=(4,6))
sb.lmplot(x="X1",y="X2",data=data,fit_reg=False)
plt.show()

<Figure size 288x432 with 0 Axes>

1 初始化聚类中心
2 所有样本点聚类（计算每个样本点与聚类中心的距离，选择最小距离的聚类中心所在的聚类作为该样本所属聚类）
3 重新计算聚类中心（每个聚类中所有样本的均值）
4 迭代执行2-3直到聚类中心不再变化（iter_num）

2 给定聚类中心，计算每个点属于哪个聚类，定义函数实现

#给定聚类中心，如何求每个样本所属的聚类
def find_closest(X,centroids):
    #样本数量
    m=X.shape[0]
    idx=np.zeros(m)
    k=centroids.shape[0]
    #遍历所有样本
    for i in range(m):
        distance=10000
        #遍历所有聚类中心
        for j in range(k): 
            #计算样本与聚类中心的距离
            dist=np.sum(np.power(X[i,:]-centroids[j,:],2))
            if dist<distance:
                distance=dist
                idx[i]=j
    return idx

#测试一下
centorids=np.arange(1,5).reshape(2,2)
centorids

array([[1, 2],
       [3, 4]])

idx=find_closest(data.values,centorids)

idx

array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 0.,
       1., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 1., 0., 0.,
       0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 1., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 1., 0., 0., 0., 0., 0., 0.,
       0., 1., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

3 根据已有的数据的标记，来重新更新聚类中心，定义相应的函数

index=np.where(idx==0)[0]
index

array([ 56, 100, 101, 103, 104, 105, 106, 107, 108, 110, 111, 112, 114,
       115, 117, 118, 119, 120, 121, 122, 124, 125, 126, 127, 128, 129,
       130, 131, 132, 133, 134, 135, 136, 137, 138, 140, 142, 143, 144,
       145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157,
       158, 159, 162, 164, 165, 166, 167, 168, 169, 170, 172, 174, 175,
       176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 188, 189,
       190, 191, 192, 193, 194, 195, 197, 198, 199], dtype=int64)

def update_centorids(X,idx,k):
    centorids=np.zeros((k,X.shape[1]))
    for i in range(k):
        index=np.where(idx==i)[0]
        centorids[i]=np.sum(X[index,:],axis=0)/len(index)
    return centorids

#测试函数
update_centorids(data.values,idx,2)

array([[2.8195125 , 0.99467112],
       [4.03762952, 3.8009101 ]])

4 初始化聚类中心，定义相应的函数

def initialize_centroid(X,k):
    np.random.seed(30)
    index_initial=[np.random.randint(1,X.shape[0]) for i in range(k)]
    centorids=np.zeros((k,X.shape[1]))
    print(index_initial)
    for i,j in enumerate(index_initial):
        centorids[i]=X[j,:]
    return centorids

#测试一下该函数
initialize_centroid(data.values,3)

[294, 141, 252]

array([[6.48212628, 2.5508514 ],
       [3.7875723 , 1.45442904],
       [6.01017978, 2.72401338]])

data.values[294]

array([6.48212628, 2.5508514 ])

5 定义K-means算法

#设计K-means算法
def k_means(X,k,iter_num):
    centroids=np.zeros((k,X.shape[1]))
    #初始化聚类中心
    centroids=initialize_centroid(X,k)
    for i in range(iter_num):
        #每个样本找到所属聚类
        idx=find_closest(X,centroids)
        print(idx)
        #更新新的聚类中心
        centroids=update_centorids(X,idx,k)
        
        print(centroids)
    return centroids,idx

centroids,idx=k_means(data.values,3,10)

[294, 141, 252]
[1. 2. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 2.
 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 2.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 2. 2. 0. 2. 2. 2. 0. 2. 2. 2. 0. 0. 0. 0. 2. 2.
 2. 0. 0. 0. 2. 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 2. 0. 2. 0. 2. 2. 1.
 2. 1. 2. 0. 0. 0. 2. 2. 2. 2. 2. 0. 2. 0. 2. 2. 2. 0. 0. 0. 0. 2. 0. 2.
 0. 1. 0. 2. 2. 2. 0. 2. 0. 1. 2. 2. 2. 2. 2. 2. 0. 2. 0. 0. 2. 2. 2. 0.
 2. 2. 2. 2. 2. 2. 0. 0. 0. 2. 2. 1.]
[[6.89324886 2.94679018]
 [2.48934355 2.89564245]
 [5.42986227 3.25759288]]
[1. 2. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 2. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 1. 1. 1. 2. 2. 0. 2. 2. 2. 0. 2. 2. 2. 0. 0. 0. 0. 0. 2.
 2. 0. 0. 0. 2. 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 2. 0. 2. 2. 1.
 0. 2. 2. 0. 0. 0. 2. 2. 2. 2. 2. 0. 2. 0. 0. 0. 2. 0. 0. 0. 0. 2. 0. 2.
 0. 1. 0. 2. 2. 2. 0. 2. 0. 2. 2. 0. 2. 2. 0. 2. 0. 2. 0. 0. 0. 0. 2. 0.
 2. 2. 2. 2. 2. 2. 0. 0. 0. 2. 0. 1.]
[[6.73758256 2.94610993]
 [2.41318124 3.02894849]
 [5.28641575 2.89315506]]
[1. 2. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 2. 1. 2. 1. 1. 2. 1. 2. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1.
 1. 2. 1. 2. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 2. 2. 1. 1.
 1. 2. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 2. 1. 2. 1. 1. 1. 1.
 1. 2. 1. 2. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 2. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 1. 1. 1. 2. 0. 0. 2. 2. 0. 0. 2. 2. 2. 0. 0. 0. 0. 0. 2.
 2. 0. 0. 0. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 0. 0. 0. 2. 0. 2. 2. 2.
 0. 2. 2. 0. 0. 0. 2. 2. 2. 0. 2. 0. 2. 0. 0. 0. 2. 0. 0. 0. 0. 2. 0. 2.
 0. 1. 0. 2. 2. 2. 0. 2. 0. 2. 2. 0. 2. 2. 0. 2. 0. 2. 0. 0. 0. 0. 2. 0.
 2. 2. 2. 2. 2. 2. 0. 0. 0. 2. 0. 1.]
[[6.68390018 2.94499954]
 [2.28558411 3.23123345]
 [5.0071835  2.44170899]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 1. 2. 1. 2. 2. 2. 2. 1. 2. 1. 1. 1. 2. 1. 1. 1. 1. 2. 1.
 2. 2. 2. 2. 2. 1. 1. 2. 1. 1. 2. 2. 1. 2. 2. 1. 1. 1. 2. 2. 2. 2. 2. 1.
 1. 2. 2. 2. 1. 1. 1. 2. 1. 1. 1. 1. 1. 1. 2. 2. 2. 2. 1. 2. 1. 1. 1. 1.
 1. 2. 1. 2. 1. 2. 2. 1. 2. 2. 1. 1. 2. 1. 1. 2. 2. 2. 2. 2. 1. 1. 1. 1.
 1. 2. 1. 1. 2. 1. 1. 1. 0. 0. 0. 2. 2. 0. 0. 2. 2. 2. 0. 0. 0. 0. 0. 2.
 2. 0. 0. 0. 0. 0. 0. 0. 2. 2. 2. 2. 2. 0. 2. 2. 0. 0. 0. 0. 0. 2. 0. 2.
 0. 2. 2. 0. 0. 0. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 2. 0. 2.
 0. 1. 0. 2. 2. 2. 0. 2. 0. 2. 0. 0. 2. 2. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0.
 2. 0. 0. 2. 2. 2. 0. 0. 0. 2. 0. 1.]
[[6.49272845 2.9926145 ]
 [2.11716681 3.6129498 ]
 [4.38057974 1.85041121]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 2. 2. 1. 2. 2. 2. 2. 1. 2. 2. 1. 1. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 1. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 2.
 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 2. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2.
 0. 2. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0.
 0. 2. 0. 2. 2. 0. 0. 2. 0. 2. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 1.]
[[6.23121683 3.03625011]
 [1.90893972 4.6245583 ]
 [3.44146283 1.24700833]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.
 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 2. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[[6.07115453 3.00350207]
 [1.95399466 5.02557006]
 [3.06584667 1.05078048]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[[6.03366736 3.00052511]
 [1.95399466 5.02557006]
 [3.04367119 1.01541041]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[[6.03366736 3.00052511]
 [1.95399466 5.02557006]
 [3.04367119 1.01541041]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[[6.03366736 3.00052511]
 [1.95399466 5.02557006]
 [3.04367119 1.01541041]]
[1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[[6.03366736 3.00052511]
 [1.95399466 5.02557006]
 [3.04367119 1.01541041]]

centroids.shape[0]

6 绘制各个聚类的图

#画图
cluster1=data.values[np.where(idx==0)[0],:]
cluster1
cluster2=data.values[np.where(idx==1)[0],:]
cluster2
cluster3=data.values[np.where(idx==2)[0],:]
cluster3

array([[3.20360621, 0.7222149 ],
       [3.06192918, 1.5719211 ],
       [4.01714917, 1.16070647],
       [1.40260822, 1.08726536],
       [4.08164951, 0.87200343],
       [3.15273081, 0.98155871],
       [3.45186351, 0.42784083],
       [3.85384314, 0.7920479 ],
       [1.57449255, 1.34811126],
       [4.72372078, 0.62044136],
       [2.87961084, 0.75413741],
       [0.96791348, 1.16166819],
       [1.53178107, 1.10054852],
       [4.13835915, 1.24780979],
       [3.16109021, 1.29422893],
       [2.95177039, 0.89583143],
       [3.27844295, 1.75043926],
       [2.1270185 , 0.95672042],
       [3.32648885, 1.28019066],
       [2.54371489, 0.95732716],
       [3.233947  , 1.08202324],
       [4.43152976, 0.54041   ],
       [3.56478625, 1.11764714],
       [4.25588482, 0.90643957],
       [4.05386581, 0.53291862],
       [3.08970176, 1.08814448],
       [2.84734459, 0.26759253],
       [3.63586049, 1.12160194],
       [1.95538864, 1.32156857],
       [2.88384005, 0.80454506],
       [3.48444387, 1.13551448],
       [3.49798412, 1.10046402],
       [2.45575934, 0.78904654],
       [3.2038001 , 1.02728075],
       [3.00677254, 0.62519128],
       [1.96547974, 1.2173076 ],
       [2.17989333, 1.30879831],
       [2.61207029, 0.99076856],
       [3.95549912, 0.83269299],
       [3.64846482, 1.62849697],
       [4.18450011, 0.45356203],
       [3.7875723 , 1.45442904],
       [3.30063655, 1.28107588],
       [3.02836363, 1.35635189],
       [3.18412176, 1.41410799],
       [4.16911897, 0.20581038],
       [3.24024211, 1.14876237],
       [3.91596068, 1.01225774],
       [2.96979716, 1.01210306],
       [1.12993856, 0.77085284],
       [2.71730799, 0.48697555],
       [3.1189017 , 0.69438336],
       [2.4051802 , 1.11778123],
       [2.95818429, 1.01887096],
       [1.65456309, 1.18631175],
       [2.39775807, 1.24721387],
       [2.28409305, 0.64865469],
       [2.79588724, 0.99526664],
       [3.41156277, 1.1596363 ],
       [3.50663521, 0.73878104],
       [3.93616029, 1.46202934],
       [3.90206657, 1.27778751],
       [2.61036396, 0.88027602],
       [4.37271861, 1.02914092],
       [3.08349136, 1.19632644],
       [2.1159935 , 0.7930365 ],
       [2.15653404, 0.40358861],
       [2.14491101, 1.13582399],
       [1.84935524, 1.02232644],
       [4.1590816 , 0.61720733],
       [2.76494499, 1.43148951],
       [3.90561153, 1.16575315],
       [2.54071672, 0.98392516],
       [4.27783068, 1.1801368 ],
       [3.31058167, 1.03124461],
       [2.15520661, 0.80696562],
       [3.71363659, 0.45813208],
       [3.54010186, 0.86446135],
       [1.60519991, 1.1098053 ],
       [1.75164337, 0.68853536],
       [3.12405123, 0.67821757],
       [2.37198785, 1.42789607],
       [2.53446019, 1.21562081],
       [3.6834465 , 1.22834538],
       [3.2670134 , 0.32056676],
       [3.94159139, 0.82577438],
       [3.2645514 , 1.3836869 ],
       [4.30471138, 1.10725995],
       [2.68499376, 0.35344943],
       [3.12635184, 1.2806893 ],
       [2.94294356, 1.02825076],
       [3.11876541, 1.33285459],
       [2.02358978, 0.44771614],
       [3.62202931, 1.28643763],
       [2.42865879, 0.86499285],
       [2.09517296, 1.14010491],
       [5.29239452, 0.36873298],
       [2.07291709, 1.16763851],
       [0.94623208, 0.24522253],
       [2.73911908, 1.10072284],
       [3.96162465, 2.72025046],
       [3.45928006, 2.68478445]])

centroids

array([[6.03366736, 3.00052511],
       [1.95399466, 5.02557006],
       [3.04367119, 1.01541041]])

import matplotlib.pyplot as plt
fig,axe=plt.subplots(figsize=(6,9))
axe.scatter(cluster1[:,0],cluster1[:,1],s=10,color="red",label="cluster1")
axe.scatter(cluster2[:,0],cluster2[:,1],s=10,color="yellow",label="cluster2")
axe.scatter(cluster3[:,0],cluster3[:,1],s=10,color="green",label="cluster2")
axe.scatter(centroids[:,0],centroids[:,1],s=30,marker="+",c="k")
plt.show()

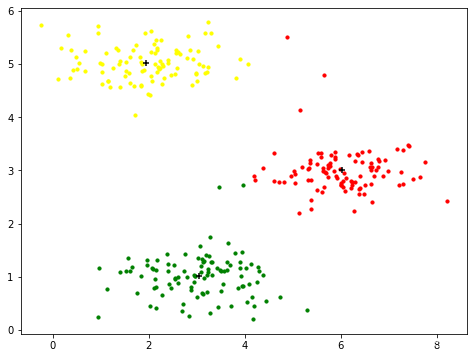
我们跳过的一个步骤是初始化聚类中心的过程。这可以影响算法的收敛。我们的任务是创建一个选择随机样本并将其用作初始聚类中心的函数。

7 定义评价函数–即任意一点所在聚类与聚类中心的距离平方和

#定义一个评价函数
def metric_square(X,idx,centroids,k):
    lst_dist=[]
    for i in range(k):
        cluster=X[np.where(idx==i)[0],:]
        dist=np.sum(np.power(cluster-centroids[i,:],2))
        lst_dist.append(dist)
    return sum(lst_dist)

cluster=data.values[np.where(idx==0)[0],:]

centroids[0,:]

array([6.03366736, 3.00052511])

np.sum(np.power(cluster-centroids[0,:],2))

82.48594291556887

#测试该函数
metric_square(data.values,idx,centroids,3)

266.65851965491936

8 使用“肘部法则”选取k值

def selecte_K(X,iter_num):
    dist_arry=[]
    for k in range(1,10):
        centroids,idx=k_means(data.values,k,iter_num)
        dist_arry.append((k,metric_square(X,idx,centroids,k)))
    best_k=sorted(dist_arry,key=lambda item:item[1])[0][0]
    return dist_arry,best_k

dist_arry,best_k=selecte_K(data.values,20)

[294]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
……
[8. 2. 0. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8.
 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8.
 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8.
 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 2. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8. 8.
 8. 8. 8. 8. 3. 7. 1. 6. 1. 3. 3. 1. 6. 1. 3. 6. 6. 1. 7. 3. 7. 4. 7. 4.
 7. 1. 7. 1. 1. 3. 3. 7. 4. 3. 7. 7. 4. 3. 3. 4. 4. 4. 1. 7. 1. 7. 7. 7.
 7. 1. 7. 1. 3. 6. 3. 3. 4. 3. 6. 4. 4. 3. 7. 3. 7. 1. 4. 1. 7. 4. 4. 4.
 6. 1. 7. 1. 4. 1. 7. 4. 1. 3. 6. 6. 3. 4. 4. 7. 3. 1. 7. 1. 3. 7. 3. 7.
 4. 7. 4. 4. 1. 4. 6. 4. 0. 0. 5. 0. 0. 0. 5. 2. 2. 2. 5. 5. 0. 5. 0. 2.
 0. 5. 5. 5. 0. 0. 0. 0. 2. 2. 2. 2. 2. 0. 2. 0. 5. 0. 0. 0. 0. 2. 0. 2.
 0. 2. 2. 5. 5. 5. 2. 2. 0. 0. 0. 5. 0. 5. 0. 0. 2. 0. 5. 5. 0. 2. 5. 0.
 5. 7. 5. 2. 2. 0. 0. 2. 5. 2. 0. 0. 0. 2. 0. 2. 5. 0. 5. 5. 0. 0. 0. 5.
 2. 0. 0. 0. 0. 2. 0. 5. 5. 2. 0. 8.]
[[6.03540601 2.90876959]
 [4.17384399 0.81938216]
 [5.05532292 3.11209335]
 [3.06175515 0.75169828]
 [2.30069511 0.99667369]
 [7.04212766 3.02764051]
 [1.44137276 0.97206476]
 [3.35444384 1.35441459]
 [1.95399466 5.02557006]]

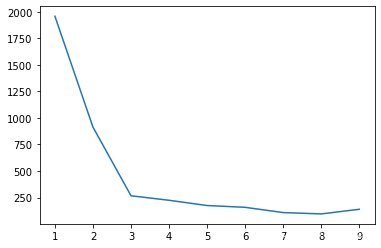
9 画张图来可视化选择K

dist_arry

[(1, 1957.654720625167),
 (2, 913.319271474709),
 (3, 266.65851965491936),
 (4, 224.19062208578683),
 (5, 174.7886069689041),
 (6, 157.8269861031051),
 (7, 108.35021878232398),
 (8, 95.72271918958536),
 (9, 139.32120386214484)]

y=[item[1] for item in dist_arry]
plt.plot(range(1,len(dist_arry)+1),y)

[<matplotlib.lines.Line2D at 0x1d875d6e1c0>]

10 对任意样本来预测其所属的聚类

### 10 对任意样本来预测其所属的聚类
def predict_cluster(x,centroids):
    lst_dist=[]
    for i in range(centroids.shape[0]):
        dist=np.sum(np.power(x-centroids[i],2))
        lst_dist.append((i,dist))
#     print(lst_dist)
    return sorted(lst_dist,key=lambda item:item[1])[0][0],lst_dist

centroids.shape[0]

x=np.array([[1.0,2.0],[1.5,2.5]])
for item in x:
    print(predict_cluster(item,centroids))

(2, [(0, 26.33885755045021), (1, 10.064180005080523), (2, 5.146008608810406)])
(2, [(0, 20.80466508259735), (1, 6.584615280794261), (2, 4.586927008121937)])

试试Sklearn

#导入包
from sklearn.cluster import KMeans
#实例化一个聚类对象
estimator = KMeans(n_clusters=3)
#用训练数据来拟合该模型
estimator.fit(data.values)
#对任意一个点进行预测
print(estimator.labels_)
estimator.predict(np.array(x))

[0 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 0]

array([1, 1])

#查看每个聚类元素到中心点的距离和
estimator.inertia_

266.6585196549193

estimator.cluster_centers_

array([[1.95399466, 5.02557006],
       [3.04367119, 1.01541041],
       [6.03366736, 3.00052511]])

from sklearn.cluster import KMeans

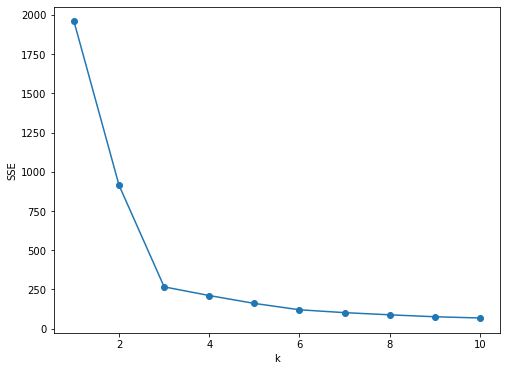
# '利用SSE选择k'
SSE = []  # 存放每次结果的误差平方和
for k in range(1, 11):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(data.values)
    SSE.append(estimator.inertia_)
X = range(1, 11)
plt.figure(figsize=(8, 6))
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X, SSE, 'o-')
plt.show()

d:\Users\DELL\anaconda3\lib\site-packages\sklearn\cluster\_kmeans.py:1036: UserWarning: KMeans is known to have a memory leak on Windows with MKL, when there are less chunks than available threads. You can avoid it by setting the environment variable OMP_NUM_THREADS=2.
  warnings.warn(

实验1 K-means实现无监督聚类

重新利用鸢尾花数据集来实现无监督的聚类，只读取鸢尾花数据集的前两列数据

from sklearn.datasets import load_iris
iris=load_iris()
data=iris.data[:,:2]
data

array([[5.1, 3.5],
       [4.9, 3. ],
       [4.7, 3.2],
       [4.6, 3.1],
       [5. , 3.6],
       [5.4, 3.9],
       [4.6, 3.4],
       [5. , 3.4],
       [4.4, 2.9],
       [4.9, 3.1],
       [5.4, 3.7],
       [4.8, 3.4],
       [4.8, 3. ],
       [4.3, 3. ],
       [5.8, 4. ],
       [5.7, 4.4],
       [5.4, 3.9],
       [5.1, 3.5],
       [5.7, 3.8],
       [5.1, 3.8],
       [5.4, 3.4],
       [5.1, 3.7],
       [4.6, 3.6],
       [5.1, 3.3],
       [4.8, 3.4],
       [5. , 3. ],
       [5. , 3.4],
       [5.2, 3.5],
       [5.2, 3.4],
       [4.7, 3.2],
       [4.8, 3.1],
       [5.4, 3.4],
       [5.2, 4.1],
       [5.5, 4.2],
       [4.9, 3.1],
       [5. , 3.2],
       [5.5, 3.5],
       [4.9, 3.6],
       [4.4, 3. ],
       [5.1, 3.4],
       [5. , 3.5],
       [4.5, 2.3],
       [4.4, 3.2],
       [5. , 3.5],
       [5.1, 3.8],
       [4.8, 3. ],
       [5.1, 3.8],
       [4.6, 3.2],
       [5.3, 3.7],
       [5. , 3.3],
       [7. , 3.2],
       [6.4, 3.2],
       [6.9, 3.1],
       [5.5, 2.3],
       [6.5, 2.8],
       [5.7, 2.8],
       [6.3, 3.3],
       [4.9, 2.4],
       [6.6, 2.9],
       [5.2, 2.7],
       [5. , 2. ],
       [5.9, 3. ],
       [6. , 2.2],
       [6.1, 2.9],
       [5.6, 2.9],
       [6.7, 3.1],
       [5.6, 3. ],
       [5.8, 2.7],
       [6.2, 2.2],
       [5.6, 2.5],
       [5.9, 3.2],
       [6.1, 2.8],
       [6.3, 2.5],
       [6.1, 2.8],
       [6.4, 2.9],
       [6.6, 3. ],
       [6.8, 2.8],
       [6.7, 3. ],
       [6. , 2.9],
       [5.7, 2.6],
       [5.5, 2.4],
       [5.5, 2.4],
       [5.8, 2.7],
       [6. , 2.7],
       [5.4, 3. ],
       [6. , 3.4],
       [6.7, 3.1],
       [6.3, 2.3],
       [5.6, 3. ],
       [5.5, 2.5],
       [5.5, 2.6],
       [6.1, 3. ],
       [5.8, 2.6],
       [5. , 2.3],
       [5.6, 2.7],
       [5.7, 3. ],
       [5.7, 2.9],
       [6.2, 2.9],
       [5.1, 2.5],
       [5.7, 2.8],
       [6.3, 3.3],
       [5.8, 2.7],
       [7.1, 3. ],
       [6.3, 2.9],
       [6.5, 3. ],
       [7.6, 3. ],
       [4.9, 2.5],
       [7.3, 2.9],
       [6.7, 2.5],
       [7.2, 3.6],
       [6.5, 3.2],
       [6.4, 2.7],
       [6.8, 3. ],
       [5.7, 2.5],
       [5.8, 2.8],
       [6.4, 3.2],
       [6.5, 3. ],
       [7.7, 3.8],
       [7.7, 2.6],
       [6. , 2.2],
       [6.9, 3.2],
       [5.6, 2.8],
       [7.7, 2.8],
       [6.3, 2.7],
       [6.7, 3.3],
       [7.2, 3.2],
       [6.2, 2.8],
       [6.1, 3. ],
       [6.4, 2.8],
       [7.2, 3. ],
       [7.4, 2.8],
       [7.9, 3.8],
       [6.4, 2.8],
       [6.3, 2.8],
       [6.1, 2.6],
       [7.7, 3. ],
       [6.3, 3.4],
       [6.4, 3.1],
       [6. , 3. ],
       [6.9, 3.1],
       [6.7, 3.1],
       [6.9, 3.1],
       [5.8, 2.7],
       [6.8, 3.2],
       [6.7, 3.3],
       [6.7, 3. ],
       [6.3, 2.5],
       [6.5, 3. ],
       [6.2, 3.4],
       [5.9, 3. ]])

iris.target

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

plt.scatter(data[:,0],data[:,1],color="blue")
plt.show()

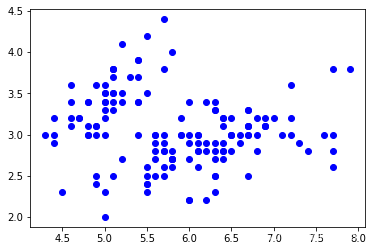
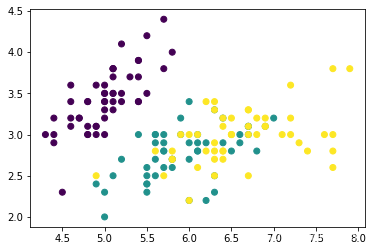
#真实的类别长成这样
plt.scatter(data[:,0],data[:,1],c=iris.target)
plt.show()

1 定义和调用更新每个样本所属聚类，聚类中心更新，初始化聚类中心的参数

def update_centorids(X,idx,k):
    centorids=np.zeros((k,X.shape[1]))
    for i in range(k):
        index=np.where(idx==i)[0]
        centorids[i]=np.sum(X[index,:],axis=0)/len(index)
    return centorids
def initialize_centroid(X,k):
    np.random.seed(30)
    index_initial=[np.random.randint(1,X.shape[0]) for i in range(k)]
    centorids=np.zeros((k,X.shape[1]))
    print(index_initial)
    for i,j in enumerate(index_initial):
        centorids[i]=X[j,:]
    return centorids

2 定义Kmeans算法获得最终的聚类中心和样本所属聚类索引

def k_means(X,k,iter_num):
    centroids=np.zeros((k,X.shape[1]))
    #初始化聚类中心
    centroids=initialize_centroid(X,k)
    for i in range(iter_num):
        #每个样本找到所属聚类
        idx=find_closest(X,centroids)
        print(idx)
        #更新新的聚类中心
        centroids=update_centorids(X,idx,k)
        print(centroids)
    return centroids,idx

centroids,idx=k_means(data,3,30)

[38, 46, 141]
[1. 0. 0. 0. 1. 1. 0. 1. 0. 0. 1. 1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 0. 1. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 0. 0. 1. 1. 0. 1. 0.
 1. 1. 2. 2. 2. 0. 2. 1. 2. 0. 2. 0. 0. 2. 2. 2. 1. 2. 1. 2. 2. 0. 1. 2.
 2. 2. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 1. 2. 2. 2. 1. 0. 0. 2. 2. 0. 1. 1.
 1. 2. 0. 1. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2.]
[[4.9137931  2.78965517]
 [5.29772727 3.44772727]
 [6.50519481 2.93506494]]
[1. 0. 0. 0. 1. 1. 0. 1. 0. 0. 1. 1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 0. 1. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 0. 0. 1. 1. 0. 1. 0.
 1. 1. 2. 2. 2. 0. 2. 1. 2. 0. 2. 0. 0. 2. 2. 2. 1. 2. 1. 2. 2. 0. 1. 2.
 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 2. 2. 1. 2. 2. 2. 1. 0. 0. 2. 2. 0. 0. 1.
 1. 2. 0. 1. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2.]
[[5.0030303  2.77272727]
 [5.28333333 3.48095238]
 [6.52666667 2.94533333]]
[1. 0. 0. 0. 1. 1. 1. 1. 0. 0. 1. 1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 0. 1. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 0. 0. 1. 1. 0. 1. 0.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 2. 2. 2. 0. 2. 1. 2. 2. 0. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 2. 2. 0. 2. 2. 2. 1. 0. 0. 2. 2. 0. 0. 1.
 0. 2. 0. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2.]
[[5.0972973  2.77027027]
 [5.2027027  3.56756757]
 [6.51842105 2.94868421]]
[1. 0. 0. 0. 1. 1. 1. 1. 0. 0. 1. 1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 0. 1. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 0. 0. 1. 1. 0. 1. 0.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 2. 2. 2. 0. 2. 0. 0. 2. 0. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 2. 0. 2. 2. 2. 0. 0. 0. 2. 0. 0. 0. 0.
 0. 2. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 2.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 2.
 2. 2. 2. 2. 2. 2.]
[[5.22391304 2.77608696]
 [5.16470588 3.61764706]
 [6.58       2.97      ]]
[1. 0. 1. 0. 1. 1. 1. 1. 0. 0. 1. 1. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 0. 1. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 0. 1. 1. 1. 0. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 2. 2. 2. 0. 2. 0. 0. 2. 0. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 2. 0. 2. 2. 2. 0. 0. 0. 2. 0. 0. 0. 0.
 0. 2. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 2.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 2.
 2. 2. 2. 2. 2. 2.]
[[5.28333333 2.73571429]
 [5.10526316 3.57368421]
 [6.58       2.97      ]]
[1. 0. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 0. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 2. 0. 2. 0. 0. 2. 0. 2. 2.
 2. 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 2. 0. 2. 2. 2. 0. 0. 0. 2. 0. 0. 0. 0.
 0. 2. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 2.
 2. 2. 2. 2. 2. 0.]
[[5.445      2.6725    ]
 [5.04318182 3.50454545]
 [6.61818182 2.99242424]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 2. 0. 2. 0. 0. 0. 0. 0. 2.
 2. 2. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 2. 2. 2. 0. 0. 0. 2. 0. 0. 0. 0.
 0. 2. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 2.
 2. 2. 2. 2. 2. 0.]
[[5.58974359 2.64102564]
 [5.01632653 3.45102041]
 [6.65645161 3.00806452]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0.
 2. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 2. 2. 0. 0. 0. 0. 2. 0. 0. 0. 0.
 0. 2. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 2. 2. 2. 0.]
[[5.65       2.64772727]
 [5.01632653 3.45102041]
 [6.70350877 3.03508772]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 2. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.70408163 2.66122449]
 [5.01632653 3.45102041]
 [6.75384615 3.05961538]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.72884615 2.68269231]
 [5.01632653 3.45102041]
 [6.79183673 3.06122449]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 2. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.76346154 2.69038462]
 [5.006      3.428     ]
 [6.80208333 3.06875   ]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 2. 2. 2. 0. 2. 0. 2. 0. 2. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0.
 0. 0. 2. 2. 2. 2. 0. 0. 0. 0. 0. 0. 0. 0. 2. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 2. 0. 2. 2. 2. 2. 0. 2. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 2. 0.
 2. 0. 2. 0. 2. 2. 0. 0. 2. 2. 2. 2. 2. 0. 0. 2. 2. 2. 0. 2. 2. 2. 0. 2.
 2. 2. 0. 2. 2. 0.]
[[5.77358491 2.69245283]
 [5.006      3.428     ]
 [6.81276596 3.07446809]]

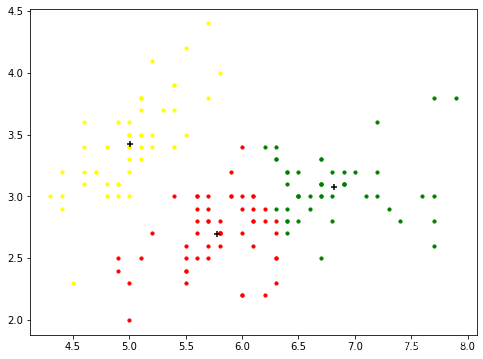
3 绘制各个聚类的图

#画图
import matplotlib.pyplot as plt
cluster1=data[np.where(idx==0)[0],:]
cluster2=data[np.where(idx==1)[0],:]
cluster3=data[np.where(idx==2)[0],:]
fig,axe=plt.subplots(figsize=(8,6))
axe.scatter(cluster1[:,0],cluster1[:,1],s=10,color="red",label="cluster1")
axe.scatter(cluster2[:,0],cluster2[:,1],s=10,color="yellow",label="cluster2")
axe.scatter(cluster3[:,0],cluster3[:,1],s=10,color="green",label="cluster2")
axe.scatter(centroids[:,0],centroids[:,1],s=30,marker="+",c="k")
plt.show()

4 定义评价函数–即任意一点所在聚类与聚类中心的距离平方和

定义一个评价函数

def metric_square(X,idx,centroids,k):
    lst_dist=[]
    for i in range(k):
        cluster=X[np.where(idx==i)[0],:]
        dist=np.sum(np.power(cluster-centroids[i,:],2))
        lst_dist.append(dist)
    return sum(lst_dist)

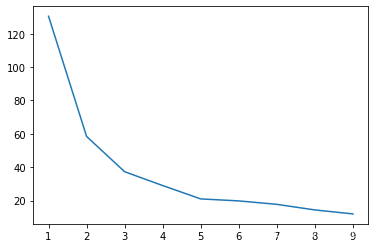
5 使用“肘部法则”选取k值

def selecte_K(X,iter_num):
    dist_arry=[]
    for k in range(1,10):
        centroids,idx=k_means(data,k,iter_num)
        dist_arry.append((k,metric_square(X,idx,centroids,k)))
    best_k=sorted(dist_arry,key=lambda item:item[1])[0][0]
    return dist_arry,best_k  
dist_arry,best_k=selecte_K(data,10)
y=[item[1] for item in dist_arry]
plt.plot(range(1,len(dist_arry)+1),y)

[38]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0.]
 ……   
[1. 0. 0. 0. 1. 1. 0. 1. 0. 0. 1. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1.
 0. 0. 1. 1. 1. 0. 0. 1. 1. 1. 0. 0. 1. 1. 0. 1. 1. 7. 0. 1. 1. 0. 1. 0.
 1. 0. 8. 6. 8. 5. 4. 5. 6. 7. 4. 7. 7. 6. 5. 6. 5. 8. 5. 5. 4. 5. 6. 4.
 4. 4. 4. 8. 8. 8. 6. 5. 5. 5. 5. 5. 5. 6. 8. 4. 5. 5. 5. 6. 5. 7. 5. 5.
 5. 4. 7. 5. 6. 5. 8. 4. 4. 2. 7. 2. 4. 8. 8. 4. 8. 5. 5. 6. 4. 3. 2. 5.
 8. 5. 2. 4. 8. 8. 4. 6. 4. 2. 2. 3. 4. 4. 4. 2. 6. 6. 6. 8. 8. 8. 5. 8.
 8. 8. 4. 4. 6. 6.]
[[4.71428571 3.16190476]
 [5.24285714 3.66785714]
 [7.51428571 2.87142857]
 [7.8        3.8       ]
 [6.34545455 2.73636364]
 [5.68518519 2.66666667]
 [6.14375    3.14375   ]
 [4.94285714 2.38571429]
 [6.825      3.13      ]]

6 对任意样本来预测其所属的聚类

def predict_cluster(x,centroids):
    lst_dist=[]
    for i in range(centroids.shape[0]):
        dist=np.sum(np.power(x-centroids[i],2))
        lst_dist.append((i,dist))
    return sorted(lst_dist,key=lambda item:item[1])[0][0],lst_dist

for item in np.array([[1.0,2.0],[2.4,1.6]]):
    print(predict_cluster(item,centroids))

(1, [(0, 23.266603773584908), (1, 18.08722), (2, 34.94272974196466)])
(1, [(0, 12.574528301886792), (1, 10.132819999999999), (2, 21.646559529198715)])

7 试试SKLERAN

#导入包
from sklearn.cluster import KMeans
estimator = KMeans(n_clusters=3)
estimator.fit(data)
print(estimator.labels_)
print(estimator.predict(np.array([[1.0,2.0],[2.4,1.6]])))
estimator.inertia_
estimator.cluster_centers_

[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 0 2 0 2 0 2 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0
 2 2 2 2 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2
 2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 0 2 2 2 0 2 2 2 0 2 2 2 0 2
 2 0]
[1 1]
array([[5.77358491, 2.69245283],
   [5.006     , 3.428     ],
   [6.81276596, 3.07446809]])