所周知，PDF文件是不能够像word/excel/ppt等文件一样，可以被随意编辑的，PDF文件往往只能够被查看，我们无法对它进行编辑，或者对上面的文字进行复制，也不能任意删除上面的页面。但是很多时候，我们可能需要对PDF文件的内容进行编辑，现在市面上有很多款可以编辑PDF文件的PDF编辑器，今天小编来给大家推荐一款好用的PDF编辑工具

推荐一：Mental AI
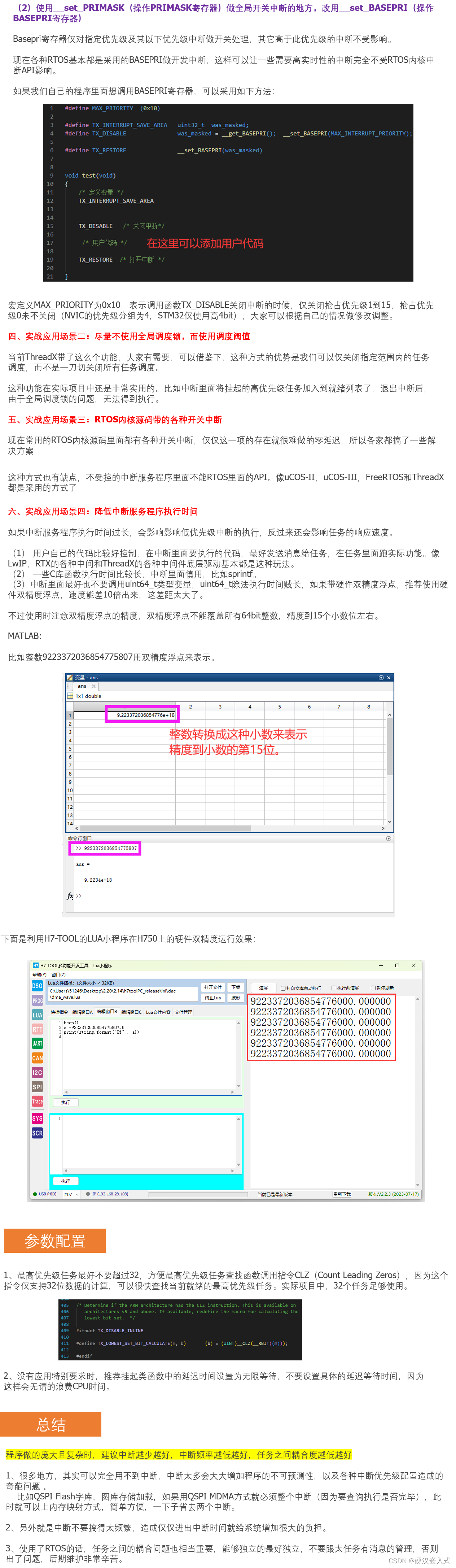
使用Mental AI的PDF解析工具
，用户可以轻松地在线或通过桌面程序编辑PDF，桌面程序比Web应用程序更有效，因为它允许编辑现有的PDF文件和扫描纸质文档。
在线版本是完全免费使用的。Mental AI的PDF解析工具在线提供许多PDF编辑功能，包括记录墨迹笔记的功能以及用于将可单击的URL附加到文件的工具。

优势：
删除编辑文本
轻松旋转和注释页面
允许从头开始创建 PDF文件

https://ai.ciyundata.com/pdf_generate
以上就是小编推荐的一款2023年受欢迎的适用于全网的PDF编辑器，大家可以根据自己的需求来选择！总的来讲，小编更偏向于推荐大家使用Mental AI的PDF编辑器，这款软件界面简洁，用户操作起来很简单，对于新手来讲也是很容易的，同时，它具备的功能也相对齐全，能够帮助你完成对于PDF的大部分需求，如果非要小编推荐一款的话，小编肯定会更倾向于推荐Mental AI的PDF编辑器的。