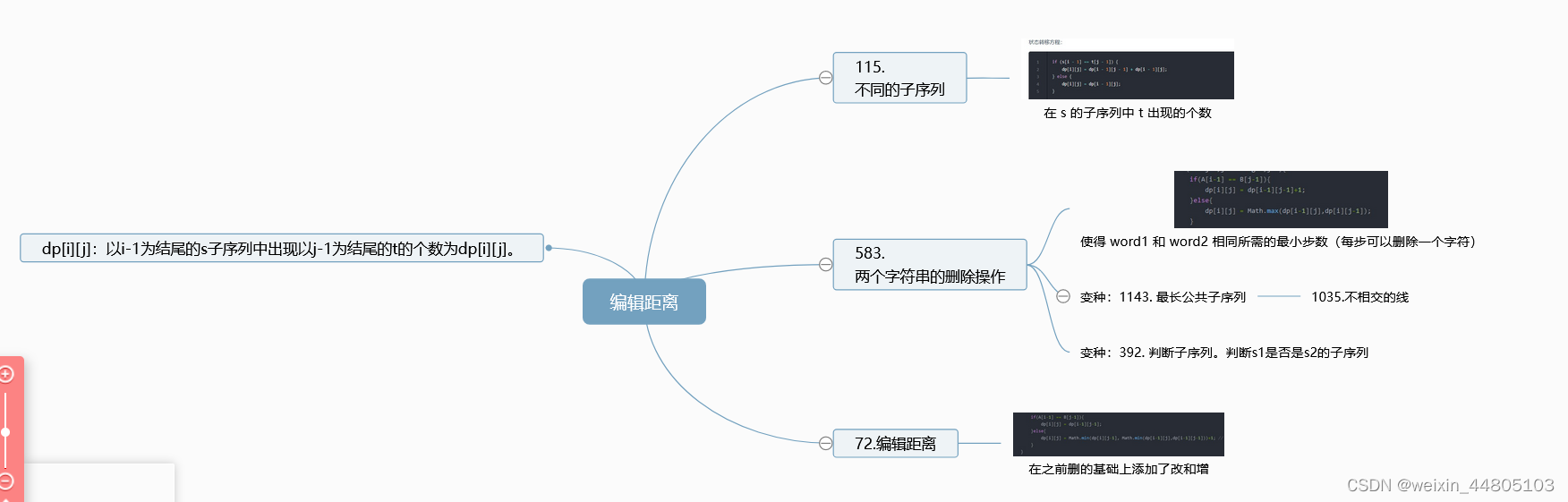
583. 两个字符串的删除操作

这道题求得的最小步数，是这道题的变种
$M in (步数） = s t r 1. l e n g t h + s t r 2. l e n g t h - 2 * (M a x (公共字符串长度）)$

class Solution {
    public int minDistance(String word1, String word2) {
    char[] A = word1.toCharArray();
    char[] B = word2.toCharArray();

    int[][] dp = new int[A.length+1][B.length+1];
    for(int i=1;i<=A.length;i++){
        for(int j=1;j<=B.length;j++){
            if(A[i-1] == B[j-1]){
                dp[i][j] = dp[i-1][j-1]+1;
            }else{
                dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
    }

    int res = A.length+B.length -2 *dp[A.length][B.length];
    return res;
    }
}

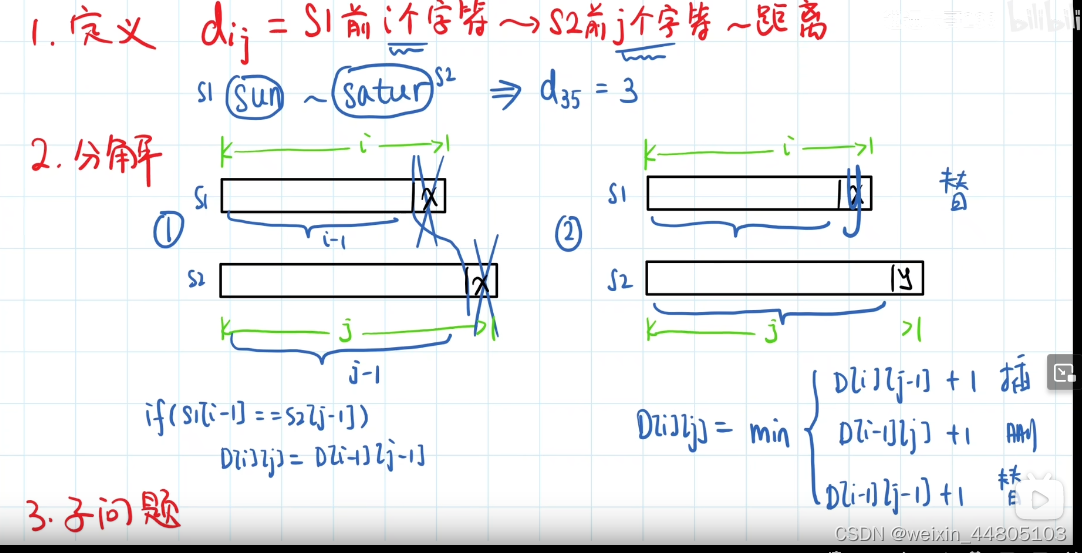
72. 编辑距离

讲的超级好，推荐！！！

$d p [i] [j]$ 表示s1的前 $i$ 个字符和说的前 $j$ 个字符相同所需要的最小的步数

在这里插入图片描述 ``

class Solution {
    public int minDistance(String word1, String word2) {
   char[] A = word1.toCharArray();
   char[] B = word2.toCharArray();

   int m = A.length;
   int n = B.length;

   int[][] dp = new int[m+1][n+1];

   for(int i=1;i<=m;i++){
       dp[i][0] = i;
   }

   for(int j =1;j<=n;j++){
       dp[0][j] = j;
   }

   for(int i =1;i<=m;i++){
        for(int j =1;j<=n;j++){
            if(A[i-1] == B[j-1]){
                dp[i][j] = dp[i-1][j-1];
            }else{
                dp[i][j] = Math.min(dp[i][j-1], Math.min(dp[i-1][j],dp[i-1][j-1]))+1; // 增-删-改
            }
        }
   }
   return dp[m][n];
    }
}