这是 LeetCode 上的「1162. 地图分析」 ，难度为「中等」。

与「单源最短路」不同，「多源最短路」问题是求从「多个源点」到达「一个/多个汇点」的最短路径。

在实现上，最核心的搜索部分，「多源 BFS」与「单源 BFS」并无区别。

并且通过建立「虚拟源点」的方式，我们可以「多源 BFS」转换回「单源 BFS」问题。

我们可以将「源点/起点」和「汇点/终点」进行反转：从每个「陆地」区域出发，多个「陆地」区域每次同时向往扩散一圈，每个「海洋」区域被首次覆盖时所对应的圈数，就是「海洋」区域距离最近的「陆地」区域的距离。

 

不过，这是如何与「单源 BFS」联系起来的呢？

我们可以想象存在一个「虚拟源点」，其与所有「真实源点」（陆地）存在等权的边，那么任意「海洋」区域与「最近的陆地」区域的最短路等价于与「虚拟源点」的最短路：

 

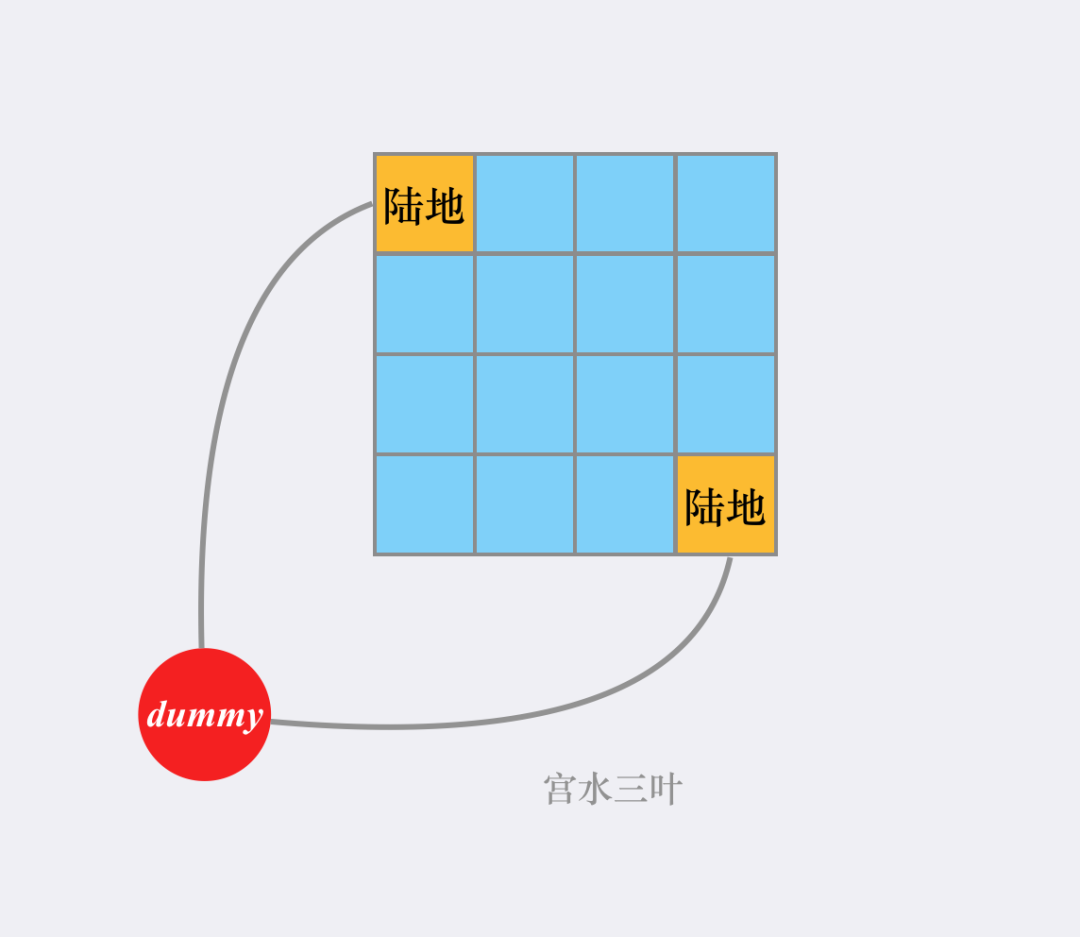
实现上，我们并不需要真的将这个虚拟源点建立出来，只需要在 BFS 前将所有的「真实源点」进行入队即可。

这个过程相当于从队列中弹出「虚拟源点」，并把它所能到点（真实源点）进行入队，然后再进行常规的 BFS 。

一些细节：实现上为了方便，在进行常规 BFS 时，如果一个「海洋」区域被访问到，说明其被离它「最近的陆地」覆盖到了，修改值为最小距离。这样我们只需要考虑那些值仍然为0 的「海洋」区域即可（代表尚未被更新）。

class Solution {
    public int maxDistance(int[][] grid) {
        int n = grid.length;
        Deque<int[]> d = new ArrayDeque<>();
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    d.add(new int[]{i, j});
                    map.put(i * n + j, 0);
                }
            }
        }
        int ans = -1;
        int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
        while (!d.isEmpty()) {
            int[] poll = d.poll();
            int dx = poll[0], dy = poll[1];
            int step = map.get(dx * n + dy);
            for (int[] di : dirs) {
                int nx = dx + di[0], ny = dy + di[1];
                if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
                if (grid[nx][ny] != 0) continue;
                grid[nx][ny] = step + 1;
                d.add(new int[]{nx, ny});
                map.put(nx * n + ny, step + 1);
                ans = Math.max(ans, step + 1);
            }
        }
        return ans;
    }
}