标准正态分布是一种均值为0、标准差为1的特殊连续概率分布。它的概率密度函数是对称的钟形曲线。
中位数绝对偏差(Median Absolute Deviation,MAD)是一种用于衡量数据集的离散程度的统计量。它衡量了观测值相对于数据集的中位数的平均偏离程度。MAD 的计算过程首先找到数据集的中位数,然后计算每个观测值与中位数的绝对差,并求这些绝对差的中位数。
标准正态分布和 MAD 的关系约为 0.6745 是基于统计推断的结果。具体为沙呢:
-
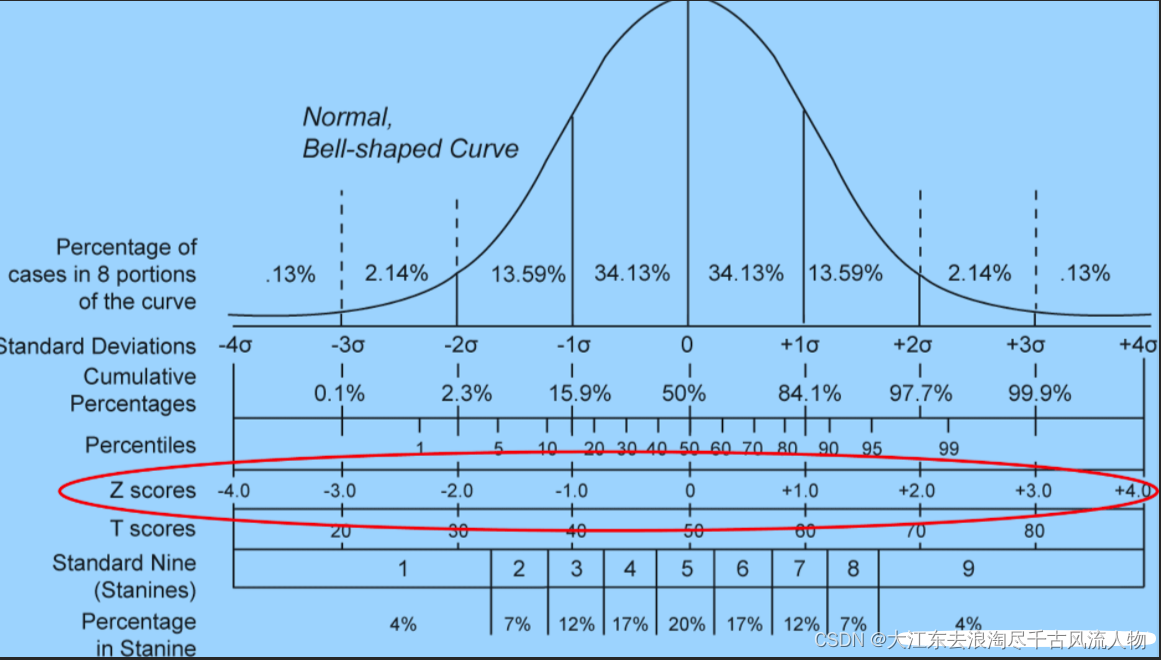
对于标准正态分布,约68% 的数据落在均值加减一个标准差的范围内,常见的3sigma原则,约95% 的数据落在均值加减两个标准差的范围内,约99.7% 的数据落在均值加减三个标准差的范围内。这是根据正态分布的性质推导出来的。
-
中位数绝对偏差(MAD)的特性是,在标准正态分布中,数据集的中位数绝对偏差大约等于标准差乘以一个常数。这个常数约为0.6745。
对于标准正态分布的观测值,约50% 的数据落在中位数加减一个中位数绝对偏差的范围内。而对于标准正态分布,中位数绝对偏差的均值是标准差的某个倍数,经过计算得到约为0.6745。因此,我们可以使用这个常数来近似地将 MAD 转换为标准差的估计值。
需要注意的是,这个关系只在标准正态分布下成立。对于其他分布,该关系可能不准确。但在实际应用中,由于 MAD 具有鲁棒性(对异常值不敏感)和简单计算等优点,因此常常用作统计中的一种离散程度衡量指标。
float MADScaleEstimator::compute(std::vector<float>& errors) const
{
CHECK(!errors.empty()) << "Error vector is empty.";
auto it = errors.begin()+std::floor(errors.size()/2);
std::nth_element(errors.begin(), it, errors.end()); // compute median
return 1.48f * (*it); // 1.48f / 0.6745
}
这段代码是一个名为 MADScaleEstimator 的函数的实现,它计算给定浮点数向量 errors 的中位数绝对偏差(Median Absolute Deviation,MAD)的估计值。
具体功能如下:
-
首先,代码使用
CHECK(!errors.empty())来确保输入的错误向量errors不为空,如果为空,则抛出异常并输出错误信息 “Error vector is empty.”。 -
然后,代码通过使用标准库函数
std::nth_element来找到errors向量的中位数。std::nth_element函数在errors.begin()和errors.end()之间找到第(errors.size()/2)个元素,并将其放置在it迭代器位置上,从而将errors向量分成两部分,左边小于中位数,右边大于等于中位数。 -
最后,代码返回
1.48f * (*it),这里使用了常量1.48f乘以中位数值(*it)来估计中位数绝对偏差(MAD)。这个系数(1.48)是一个经验值,用于将中位数绝对偏差转换成标准差估计的近似值。由于标准正态分布的标准差与 MAD 的关系约为 0.6745,因此1.48f / 0.6745用于进行该转换。
提供了一种通过计算浮点数向量的中位数和应用常量倍数来估计中位数绝对偏差的功能。