💖作者：小树苗渴望变成参天大树🎈
🎉作者宣言：认真写好每一篇博客💤
🎊作者gitee:gitee✨
💞作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法🎄
如果你喜欢作者的文章，就给作者点点关注吧！

文章目录

前言
第二十七题：[300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/)
第二十八题：[376. 摆动序列](https://leetcode.cn/problems/wiggle-subsequence/)
第二十九题：[673. 最长递增子序列的个数](https://leetcode.cn/problems/number-of-longest-increasing-subsequence/)
第三十题：[646. 最长数对链](https://leetcode.cn/problems/maximum-length-of-pair-chain/)
第三十一题：[1218. 最长定差子序列](https://leetcode.cn/problems/longest-arithmetic-subsequence-of-given-difference/)
第三十二题：[873. 最长的斐波那契子序列的长度](https://leetcode.cn/problems/length-of-longest-fibonacci-subsequence/)
第三十三题：[1027. 最长等差数列](https://leetcode.cn/problems/longest-arithmetic-subsequence/)
第三十四题：[446. 等差数列划分 II - 子序列](https://leetcode.cn/problems/arithmetic-slices-ii-subsequence/)

前言

今天我们开始讲解关于子序列数组的动态规划算法相关的题型，这个题型和子数组题型的分析有点相似，都是以什么位置为结尾然后分开讨论，但是每题的条件又是不同的，所以也是有分析难度的，博主媒体会详细的给大家介绍，大家不用担心。

第二十七题：300. 最长递增子序列

这题是我们子序列的最经典题型，后面讲的题目都是按照这题的思路来解题，所以这题是非常关键的，我会详细的给大家讲解一下。

动态规划算法：

1. 状态表示：经验+题目要求

dp[i]表示：以i位置为结尾的所有子序列中，最长子序列的长度

2. 状态转移方程：

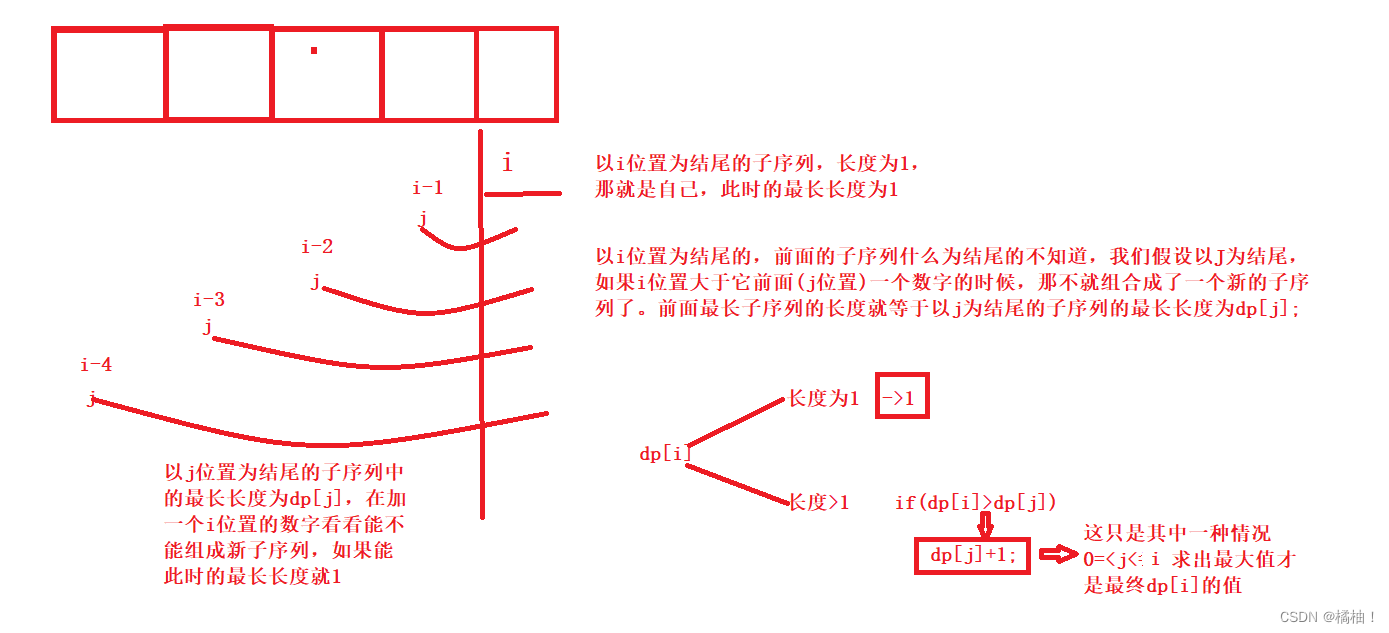
if(nums[i]>nums[j])

    dp[i]=dp[j]+1;

3. 初始化：保证数组不越界
我们发现不管怎么样自身都是一个子序列，所以长度最少都为1，所以我们dp表的第一种单独作为一个子序列的情况就不用考虑了，所以我们一开始就都初始化为1
4. 填表顺序：
从左往右
5. 返回值:
通过状态表示来看，我们以任意位置都有可能是最长子序列数组，所以应该返回dp表中的最大值

代码实现：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        //1.创建dp表+初始化
        vector<int> dp(n,1);
        int ret=1;
        //填表
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[j]<nums[i])
                {
                    dp[i]=max(dp[j]+1,dp[i]);
                }
            }
            ret=max(ret,dp[i]);
        }
        //返回值
        return ret;
    }
};

运行结果：

第二十八题：376. 摆动序列

题目解析：

动态规划算法：
1. 状态表示：经验+题目要求
这题和子数组系列中的乘积为最大正数的最长数组那题非常像，因为他要考虑前面的子数组到底最后的乘积是多少，可能为正也可能为负，所以我们需要定义两个状态表示，这题也是一样的，前面的摆动子序列最后一个是“上升”，还是“下降”状态，这样就没办法知道最后一个元素和前面是上升状态对，还是下降状态对，所以我们也定义两个状态表示：

f[i]表示：以i位置为结尾，所有子序列数组中，最后是“上升”趋势的最长子序列的长度

g[i]表示：以i位置为结尾，所有子序列数组中，最后是“下降”趋势的最长子序列的长度

2. 状态转移方程：
我们的分析还是和上题的分析是一样的，子序列的问题因为不是连续的，最后一个和前面一个位置不是连续的，前面的任何位置都有可能，所以此时需要一个变量j来控制前面的一部分的结尾部分，所有子序列问题一半都比子数组问题多一个循环条件，我们来看这题的状态转移方程的分析：

if(nums[j]<nums[i])

                f[i]=max(f[i],g[j]+1);

if(nums[j]>nums[i])

                g[i]=max(g[i],f[j]+1);

3. 初始化：保证数组不越界
和上题一样，我们不管以什么位置为结尾，序列长度最少都为1，所哟我们都初始化为1就可以了，那我们两个状态转移方程的的第一种情况都不用考虑了。

两个表都初始化为1

4. 填表顺序：
从左往右，两个表一起填写
5. 返回值:
因为不知道那个位置结尾的摆动序列最长，也不知道最后是什么趋势，最后返回值是两边当中的最大值

return max(Max,max(f[i],g[i]));

代码实现：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        //创建dp表和初始化
        vector<int> f(n,1);
        auto g=f;
        int Max=1;
        //填表
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=i;j++)
            {
                if(nums[i]>nums[j])
                {
                    f[i]=max(f[i],g[j]+1);
                }
                if(nums[i]<nums[j])
                {
                    g[i]=max(g[i],f[j]+1);
                }

            }
            Max=max(Max,max(f[i],g[i]));//一边填表一边找出最大值
        }
        //返回值
        return Max;
    }
};

运行结果：

第二十九题：673. 最长递增子序列的个数

题目解析：

先讲解一个小算法：求最大值出现的次数（只能比遍历一次数组）

来看代码：

int main()
{
	int nums[] = { 2,2,3,1,3,2,1,0 };
	int maxval = nums[0];
	int count = 1;
	for (int i = 0; i < 8; i++)
	{
		if (nums[i] == maxval)count++;
		else if (nums[i] > maxval)maxval = nums[i], count=1;
	}
	cout << maxval << " " << count << endl;
	return 0;
}

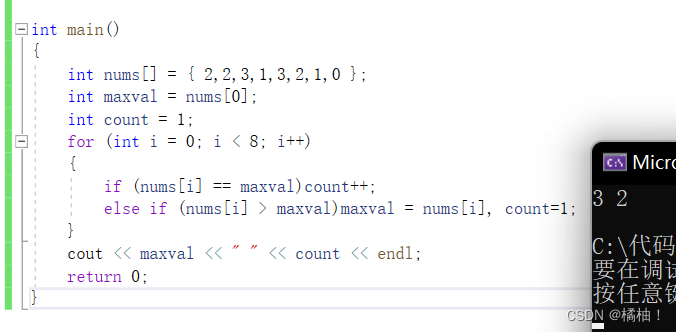
知道这个算法以后我们再来做这个题目就简单了。

动态规划算法：

1. 状态表示：经验+题目要求
通过题目要求我们要定义两个状态表示：

len[i]表示：以i位置为结尾，所有递增子序列中的最长子序列的长度
count[i]表示：以i位置为结尾，所有递增子序列中的最长子序列的个数

2. 状态转移方程：
我们的len[i]应该为
if(nums[i]>nums[j])

    len[i]=max(len[j]+1,len[i]);

为了和count[i]一起，我们修改成下面的场景

if(nums[j] < nums[i]) 这个前提下才能构成递增子序列

            if(len[j] + 1 == len[i])
                count[i] += count[j];
            else if(len[j] + 1 > len[i]) // 重新计数
                len[i] = len[j] + 1, count[i] = count[j];

3. 初始化：保证数组不越界
不管怎样自身都可以构成递增子序列，所以两个表都初始化为1
4. 填表顺序：
从左往右，两表同时填
5. 返回值:
因为不知道那个位置的子序列最长，所以也要找出最长长度，看出现的次数
还是按照之前那的小算法

代码实现：

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
    int n = nums.size();
    vector<int> len(n, 1), count(n, 1); // 1. 创建 dp 表 + 初始化
    int retlen = 1, retcount = 1; // 记录最终结果
    for(int i = 1; i < n; i++) // 2. 填表
    {
        for(int j = 0; j < i; j++)
        {
            if(nums[j] < nums[i])
            {
                if(len[j] + 1 == len[i])
                    count[i] += count[j];
                else if(len[j] + 1 > len[i]) // 重新计数
                    len[i] = len[j] + 1, count[i] = count[j];
            }
        }
        if(retlen == len[i])
            retcount += count[i];
        else if(retlen < len[i]) // 重新计数
            retlen = len[i], retcount = count[i];
    }
    // 3. 返回结果
    return retcount;
    }   
};

运行结果：

第三十题：646. 最长数对链

题目解析：

预处理：排序

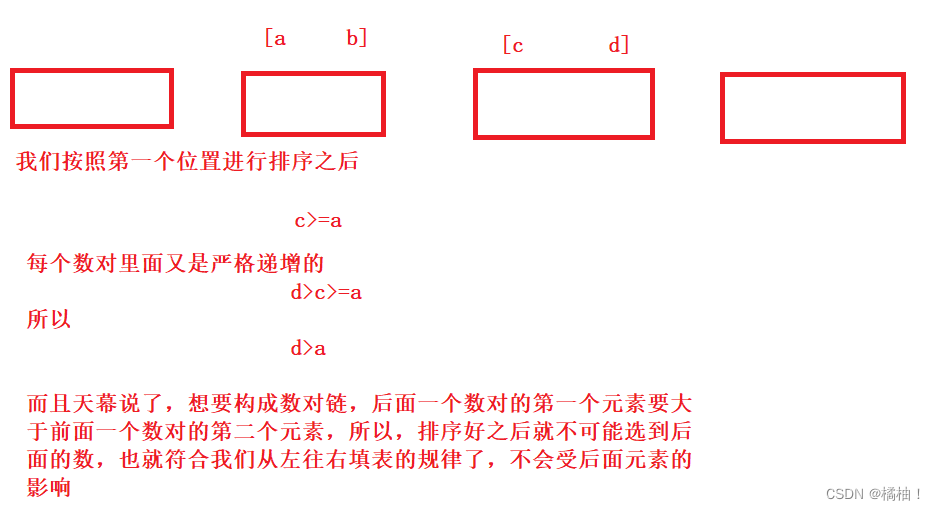
动态规划算法：
1. 状态表示：经验+题目要求

dp[i]表示：以第i行位置为结尾的最长数对链的长度

2. 状态转移方程：
分析方法时前面时一样的，把一个数对堪称一个整体
在这里插入图片描述

if(nums[i][0]>nums[j][1])

                dp[i]=dp[j]+1;

3. 初始化：保证数组不越界
按照最坏的情况去初始化，最少的数对链长度都为1，所以全部初始化为1
4. 填表顺序：
从左往右
5. 返回值:
不知道以哪个位置结尾的数对链最长，所以是返回dp表里面的最大值，这个可以一边填表一个找出来最大值
代码实现：

class Solution {
public:
    int findLongestChain(vector<vector<int>>& nums) {

        sort(nums.begin(),nums.end());
        int n=nums.size();
        vector<int> dp(n,1);
        int ret=1;
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[i][0]>nums[j][1])
                {
                    dp[i]=max(dp[j]+1,dp[i]);
                }
            }
            ret=max(ret,dp[i]);
        }
        return ret;
    }
};

运行结果：

第三十一题：1218. 最长定差子序列

题目解析：

动态规划算法：

1. 状态表示：经验+题目要求

dp[i]表示：以i位置的元素为结尾构成的定差子序列中最长定差子序列的长度

2. 状态转移方程：

hash[arr[i]]=hash[arr[i]-difference]+1;

3. 初始化：保证数组不越界
这题是通过元素当成下标，也没有负数，所以不需要初始化hash的第一个元素
4. 填表顺序：
从左往右
5. 返回值:
返回hash表里面的最大值

代码实现：

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
       unordered_map<int,int> hash;//第一个int是下标，表示第i个元素
       int ret=1;
       for(int i=0;i<arr.size();i++)
       {
           hash[arr[i]]=hash[arr[i]-difference]+1;
           //dp[i]=dp[j]+1;判断条件为arr[i]-difference

           ret=max(hash[arr[i]],ret);
       }
     return ret;
    }
};

运行结果：

第三十二题：873. 最长的斐波那契子序列的长度

题目解析：

动态规划算法：

1. 状态表示：经验+题目要求

dp[i][j]表示：以i位置以及j位置的元素为结尾的斐波那契子序列种最长的斐波那契子序列的长度，i位置在j位置前面，这样就保证i不等于j,方便初始化

2. 状态转移方程：

3. 初始化：保证数组不越界

因为我们dp[i][j]里面存放的是长度而且不会只有一个元素的情况，所以把dp[i][j]都初始化为2，只会使用到i<j位置的值，其余的值初始化什么都无所谓，使用不到的，所以索性都初始化为2.

4. 填表顺序：
从上往下
我们的j是最后一个位置，所以从第2个位置开始算才有意义
我们的i是最后一个位置的前一个位置，所以从第1个位置开始算才有意义
5. 返回值:
我们不知道以那两个位置为结尾时候的长度最长，所以返回dp表里面的最大值，但是我们的最短长度都应该是3，如果找到就返回0，此时dp表里面的值最小都为2，所以要判断一下ret<3?0:ret

代码实现：

class Solution {
public:
    int lenLongestFibSubseq(vector<int>& arr) {
        int n=arr.size();
        unordered_map<int,int> hash;
        for(int i=0;i<n;i++)
        {
            hash[arr[i]]=i;//将arr中的下标和元素绑定
        }

        //创建一个二维dp表，并初始化为2
        vector<vector<int>> dp(n,vector<int>(n,2));

        //填表，注意i，j起始位置
        int ret=2;
        for(int j=2;j<n;j++)
        {
            for(int i=1;i<j;i++)
            {
                int a=arr[j]-arr[i];
                if(a<arr[i]&&hash.count(a))
                {
                    dp[i][j]=dp[hash[a]][i]+1;
                    //dp[i][j]=dp[k][i]+1;
                }
                ret=max(ret,dp[i][j]);//确定一个dp[i][j]就判断是不是最大值
            }
        }
        return ret<3?0:ret;
    }
};

运行结果：

第三十三题：1027. 最长等差数列

题目解析：

动态规划算法：

1. 状态表示：经验+题目要求
这个和上面的题目有点类似，以i位置为结尾的元素的能否和前面构成等差数列，是需要前面两个位置的值，不像子数组问题，是连续的，前面两个元素的位置就是i-1和I-2位置的值，但是子序列问题不是的，所以不行，斐波那契和等差数列都是需要前面两个位置的值才能办证后面的值能否推出来，也就是有了后两个元素的值，就能推出来倒数第三个元素的值，所以此题的状态表示为：

dp[i][j]表示：以i位置的元素及j位置的元素为结尾的所有子序列中，最长等差子序列的长度

2. 状态转移方程：

3. 初始化：保证数组不越界
初始化使得将dp表里面的值都初始化为2，hash的第一个位置初始化0；
4. 填表顺序：
有两种：

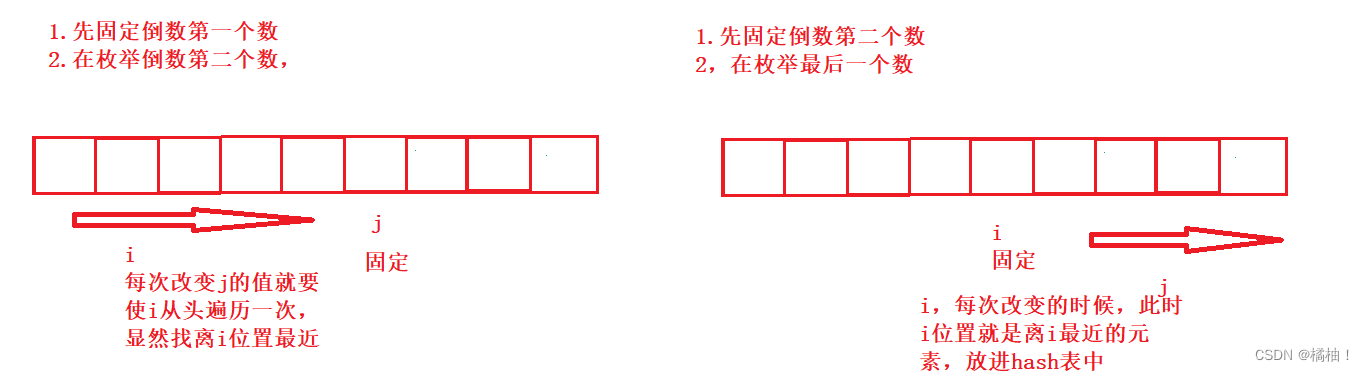
5. 返回值:
返回值dp表中的最大值

代码实现：

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) {
        int n=nums.size();
        unordered_map<int,int> hash;
        hash[nums[0]]=0;

        vector<vector<int>> dp(n,vector<int>(n,2));

        int ret=2;
        for(int i=1;i<n;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                int a=2*nums[i]-nums[j];
                if(hash.count(a))
                {
                    dp[i][j]=dp[hash[a]][i]+1;
                }
                ret=max(ret,dp[i][j]);
            }
            hash[nums[i]]=i;
        }
        return ret;
    }
};

运行结果：

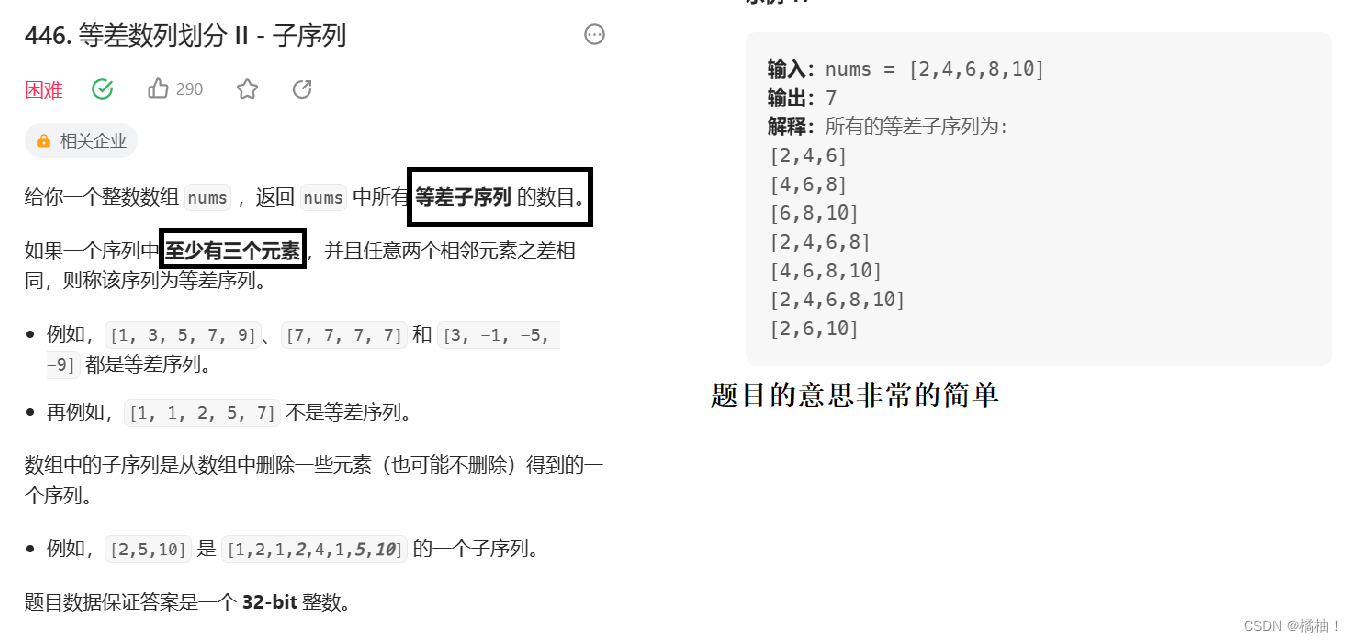
第三十四题：446. 等差数列划分 II - 子序列

题目解析：

动态规划算法：

1. 状态表示：经验+题目要求
这个题目第29题还有33题很像，将他们的思想结合起来了，我们的等差数列，将状态表示定位dp[i]是不行的，原因是你要求的dp[i]肯定是需要使用到dp[i-1],dp[i-2]等位置的值，显然没有办法知道公差是多少，最少需要三个数，所以我们要将状态表示定义为dp[i][j]表示最后两个位置的值，往前面推导

dp[i][j]表示：以i位置以及j位置为结尾的所有等差数列的个数（i<j）

2. 状态转移方程：
这种状态转移方程为了少一个循环，通常会将值放在hash表里面，直接通过元素定位到对应的下标，元素过多就把hash表里面的值定义成一个数组类型，是存放原数组下标的数组，顶多遍历这个下标数组就可以了。

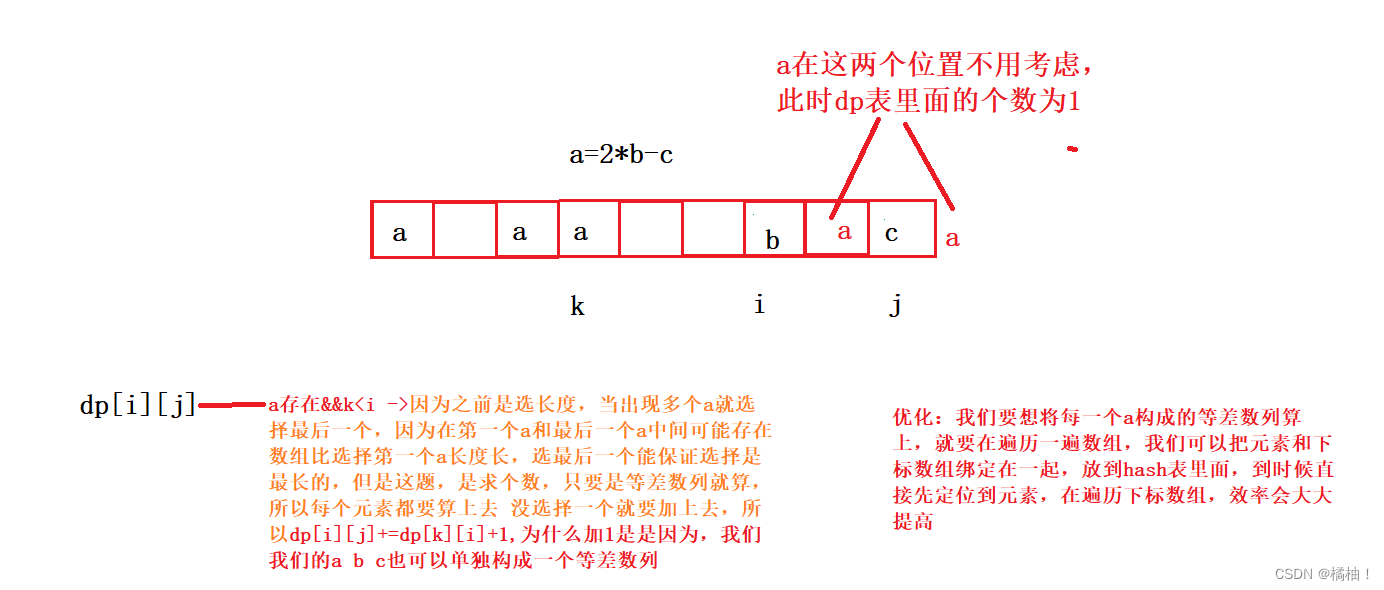
3. 初始化：保证数组不越界

我们单独的两个元素不构成等差数列，所以将dp表全部初始化为0

4. 填表顺序：

我们先固定倒数第一个数j，从下标为2的地方开始遍历才有意义
在枚举倒数第二个数i，从下标为1的地方开始遍历才有意义

5. 返回值:
返回dp表里面所有值的和

代码实现：

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n=nums.size();
        unordered_map<long long,vector<int>> hash;
        for(int i=0;i<n;i++)//将原数组元素和下标数组绑定
        {
            hash[nums[i]].push_back(i);
        }
        int sum=0;
        vector<vector<int>> dp(n,vector<int>(n));//创建dp表
        for(int j=2;j<n;j++)
        {
            for(int i=1;i<j;i++)
            {
                long long a=(long long)2*nums[i]-nums[j];//防止溢出
                if(hash.count(a))//判断a存不存在
                {
                    for(auto k:hash[a])//遍历下标数组，为a的元素不止一个
                    {
                        if(k<i)
                        {
                            dp[i][j]+=dp[k][i]+1;
                        }
                    }
                }
                sum+=dp[i][j];//求和
            }
        }
        //返回值
        return sum;
    }
};