文章目录
- 1. 前言
- 1.1 EM的介绍
- 1.2 EM的应用场景
- 2. 高斯混合模型估计
- 2.1 导入函数
- 2.2 创建数据
- 2.3 初始化
- 2.4 Expectation Step
- 2.5 Maximization step
- 2.6 循环迭代可视化
- 3. 多维情况
- 4. 讨论
1. 前言
1.1 EM的介绍
(Expectation-Maximization,EM)是一种迭代式的优化算法,主要用于解决含有隐变量的概率模型的参数估计问题。它的目标是在给定观测数据和未观测数据(隐变量)的情况下,估计概率模型的参数,使得模型能够最好地拟合观测数据。
EM算法的基本思想是通过交替进行两个步骤来优化模型参数:E步骤(Expectation)和M步骤(Maximization)。
-
E步骤(
Expectation):
在E步骤中,我们根据当前的参数估计值,计算出每个观测数据属于每个隐变量状态的概率,即计算出每个观测数据的后验概率。这些后验概率称为期望,因为它们代表了在当前参数下观测数据所“期望”的隐变量状态。 -
M步骤(
Maximization):
在M步骤中,我们根据E步骤得到的后验概率,最大化对数似然函数(或者叫Q函数)来更新模型参数。这一步骤可以看作是在给定观测数据和当前隐变量的情况下,对模型参数进行最大似然估计。
通过反复迭代E步骤和M步骤,EM算法不断优化模型参数,直到达到收敛条件。最终得到的模型参数能够使得模型对观测数据的拟合效果达到最优。
优点:
-
强大的参数估计能力:EM算法在含有隐变量的概率模型中具有较强的参数估计能力,尤其对于复杂模型和大规模数据集表现出色。
-
高效的迭代优化:EM算法采用迭代的方式优化参数,通常能够在有限的迭代次数内收敛到局部最优解,相比其他优化方法更高效。
-
灵活性:EM算法可以用于广泛的机器学习任务,包括聚类、混合高斯模型、隐马尔可夫模型等,使其在不同领域中得到广泛应用。
-
统计性解释:EM算法基于最大似然估计,提供了对模型参数的统计性解释,能够在一定程度上量化参数估计的不确定性。
缺点:
-
收敛性不稳定:EM算法对于参数的初始值敏感,可能会陷入局部最优解,导致收敛性不稳定。
-
需要选择合适的迭代次数:EM算法的收敛速度取决于迭代次数的选择,过多或过少的迭代次数都可能影响参数估计的精度。
-
对高维数据敏感:在高维数据上,EM算法可能会面临维度灾难和过拟合问题,导致模型性能下降。
-
可能陷入局部最优解:EM算法是一种局部优化方法,可能会陷入局部最优解,而无法得到全局最优解。
1.2 EM的应用场景
EM算法主要是用于参数估计,特别是在一些含有隐变量的概率模型,因此应用领域相对广泛:
-
计算机视觉:在图像处理和计算机视觉中,EM算法可以用于图像分割、目标识别和人脸识别等任务,特别是在混合高斯模型和高斯混合模型中的应用较为广泛。
-
自然语言处理:在自然语言处理领域,EM算法常用于文本聚类、主题模型和情感分析等任务,例如隐含狄利克雷分布模型(Latent Dirichlet Allocation,LDA)就是一种常见的应用。
-
生物信息学:在基因组学和蛋白质结构预测中,EM算法可以用于基因表达聚类、DNA序列分析和蛋白质折叠等问题。
-
金融领域:在金融风险评估、投资组合优化和市场预测中,EM算法可以用于建模和预测复杂的金融数据。
-
推荐系统:在个性化推荐和协同过滤任务中,EM算法可以用于学习用户和物品的隐含因子,从而实现更准确的推荐。
-
医学图像分析:在医学影像处理和分析中,EM算法可以用于图像分割、病灶检测和医学图像重建等任务。
-
无线通信:在无线信号处理和通信中,EM算法可以用于信号检测、通信信道估计和信号解调等问题。
2. 高斯混合模型估计
EM算法通常用于无监督学习问题,这里就用简单的高斯混合模型(
GMM)作实战演示,此外还有隐马尔可夫模型(HMM)也是挺常见的。
2.1 导入函数
import random
import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
2.2 创建数据
m1 = [1, 1]
m2 = [7, 7]
cov1 = [[3, 2], [2, 3]]
cov2 = [[2, -1], [-1, 2]]
x = np.random.multivariate_normal(m1, cov1, size=(200,))
y = np.random.multivariate_normal(m2, cov2, size=(200,))
d = np.concatenate((x, y), axis=0)
查看分布情况
plt.figure(figsize=(10,10))
plt.scatter(d[:,0], d[:,1], marker='o')
plt.axis('equal')
plt.xlabel('X-Axis', fontsize=16)
plt.ylabel('Y-Axis', fontsize=16)
plt.title('Ground Truth', fontsize=22)
plt.grid()
plt.show()

2.3 初始化
这里是在进行EM算法前对两个高斯分布的均值和协方差矩阵初始,其中参数pi初始化为 0.5,表示两个高斯分布的先验概率相等
m1 = random.choice(d)
m2 = random.choice(d)
cov1 = np.cov(np.transpose(d))
cov2 = np.cov(np.transpose(d))
pi = 0.5
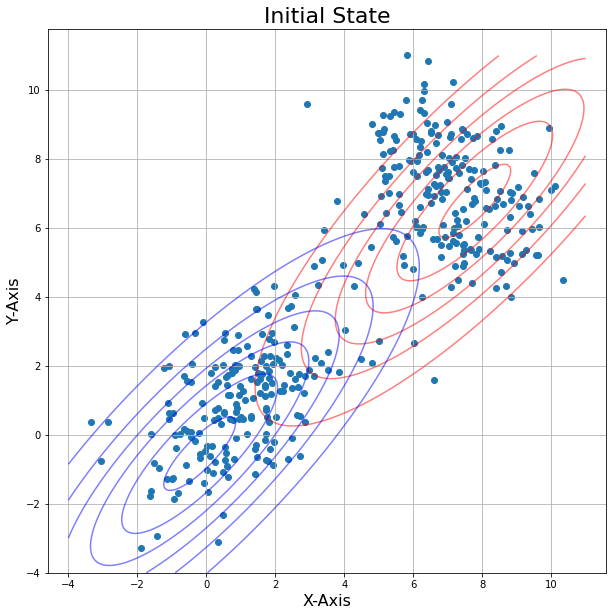
可视化高斯分布情况(等高线)
x1 = np.linspace(-4, 11, 200)
x2 = np.linspace(-4, 11, 200)
X, Y = np.meshgrid(x1, x2)
Z1 = multivariate_normal(m1, cov1)
Z2 = multivariate_normal(m2, cov2)
pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X
pos[:, :, 1] = Y
plt.figure(figsize=(10, 10))
plt.scatter(d[:, 0], d[:, 1], marker='o')
plt.contour(X, Y, Z1.pdf(pos), colors="r", alpha=0.5)
plt.contour(X, Y, Z2.pdf(pos), colors="b", alpha=0.5)
plt.axis('equal')
plt.xlabel('X-Axis', fontsize=16)
plt.ylabel('Y-Axis', fontsize=16)
plt.title('Initial State', fontsize=22)
plt.grid()
plt.show()
2.4 Expectation Step
计算数据点对应于每个类别的"期望"
def Estep(lis1):
m1=lis1[0]
m2=lis1[1]
cov1=lis1[2]
cov2=lis1[3]
pi=lis1[4]
pt2 = multivariate_normal.pdf(d, mean=m2, cov=cov2)
pt1 = multivariate_normal.pdf(d, mean=m1, cov=cov1)
w1 = pi * pt2
w2 = (1-pi) * pt1
eval1 = w1/(w1+w2)
return(eval1)
2.5 Maximization step
使用E步骤中得到的隐含变量的估计值,来最大化(最优化)模型的对数似然函数
def Mstep(eval1):
num_mu1,din_mu1,num_mu2,din_mu2=0,0,0,0
for i in range(0,len(d)):
num_mu1 += (1-eval1[i]) * d[i]
din_mu1 += (1-eval1[i])
num_mu2 += eval1[i] * d[i]
din_mu2 += eval1[i]
mu1 = num_mu1/din_mu1
mu2 = num_mu2/din_mu2
num_s1,din_s1,num_s2,din_s2=0,0,0,0
for i in range(0,len(d)):
q1 = np.matrix(d[i]-mu1)
num_s1 += (1-eval1[i]) * np.dot(q1.T, q1)
din_s1 += (1-eval1[i])
q2 = np.matrix(d[i]-mu2)
num_s2 += eval1[i] * np.dot(q2.T, q2)
din_s2 += eval1[i]
s1 = num_s1/din_s1
s2 = num_s2/din_s2
pi = sum(eval1)/len(d)
lis2=[mu1,mu2,s1,s2,pi]
return(lis2)
2.6 循环迭代可视化
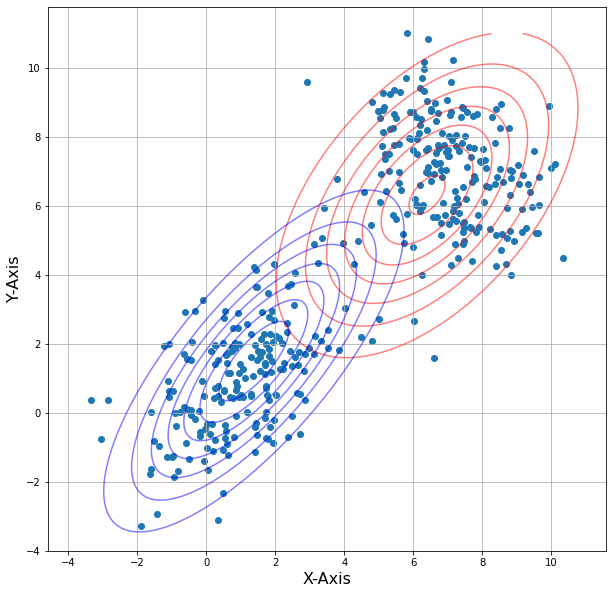
这里修改迭代次数(i)分别为1,2,3,4,结果:
iterations = 20
lis1=[m1,m2,cov1,cov2,pi]
for i in range(0,iterations):
lis2 = Mstep(Estep(lis1))
lis1=lis2
if(i==0 or i == 4 or i == 9 or i == 14 or i == 19):
plot(lis1)
i = 0:
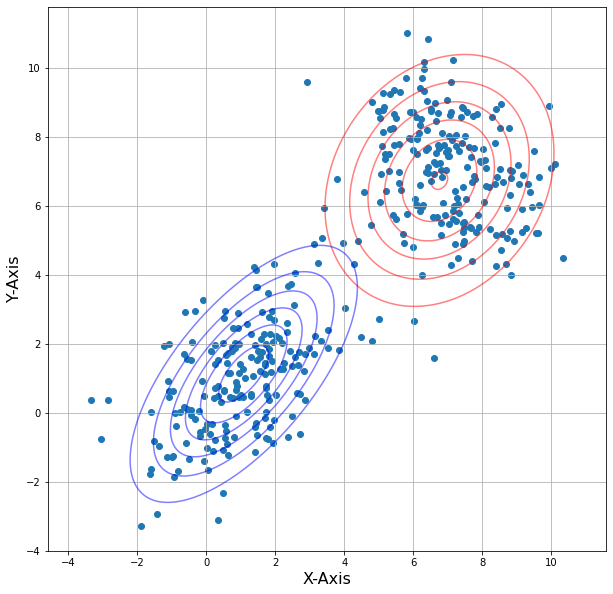
i = 1:
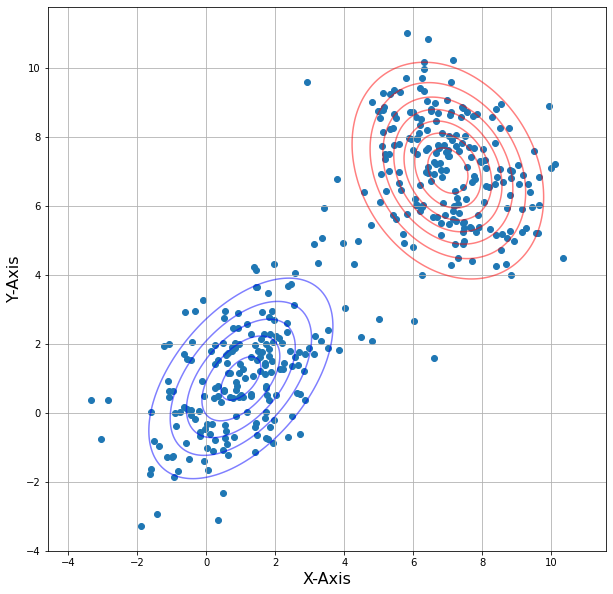
i = 2:
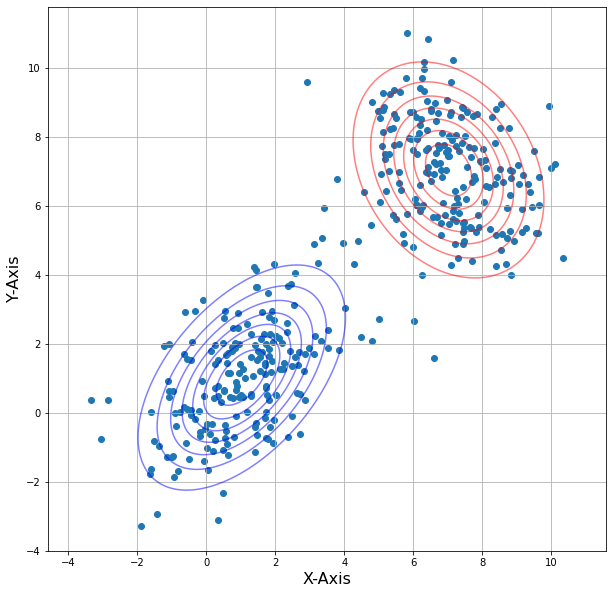
i = 3:
i = 4:
当i越大,等高线的重叠程度越小,说明经过更多的迭代,高斯混合模型的参数估计越接近真实值,模型的拟合效果越好。根据结果可以看到在第二次迭代后两个模型等高线几乎没有变化,这表示模型已经收敛到一个稳定状态。在EM算法中,迭代会持续更新参数,直到收敛到一个局部最优解或全局最优解为止。
当模型达到收敛状态后,后续的迭代可能不会有显著的变化,因为模型已经找到了最优解或接近最优解。此时,进一步迭代可能只会导致细微的调整,不会对整体结果产生重大影响。
3. 多维情况
有小伙伴会问如果我一个数据集有多个分组,直接上:GMM的建模代码和刚刚一样
import matplotlib.pyplot as plt
from matplotlib import style
style.use('fivethirtyeight')
from sklearn.datasets import make_blobs
import numpy as np
from scipy.stats import multivariate_normal
# 0. Create dataset
X, Y = make_blobs(cluster_std=1.5, random_state=20, n_samples=500, centers=3)
# Stratch dataset to get ellipsoid data
X = np.dot(X, np.random.RandomState(0).randn(2, 2))
class GMM:
def __init__(self,X,number_of_sources,iterations):
self.iterations = iterations
self.number_of_sources = number_of_sources
self.X = X
self.mu = None
self.pi = None
self.cov = None
self.XY = None
def run(self):
self.reg_cov = 1e-6*np.identity(len(self.X[0]))
x,y = np.meshgrid(np.sort(self.X[:,0]),np.sort(self.X[:,1]))
self.XY = np.array([x.flatten(),y.flatten()]).T
self.mu = np.random.randint(min(self.X[:,0]),max(self.X[:,0]),size=(self.number_of_sources,len(self.X[0])))
self.cov = np.zeros((self.number_of_sources,len(X[0]),len(X[0])))
for dim in range(len(self.cov)):
np.fill_diagonal(self.cov[dim],5)
self.pi = np.ones(self.number_of_sources)/self.number_of_sources
log_likelihoods = []
fig = plt.figure(figsize=(10,10))
ax0 = fig.add_subplot(111)
ax0.scatter(self.X[:,0],self.X[:,1])
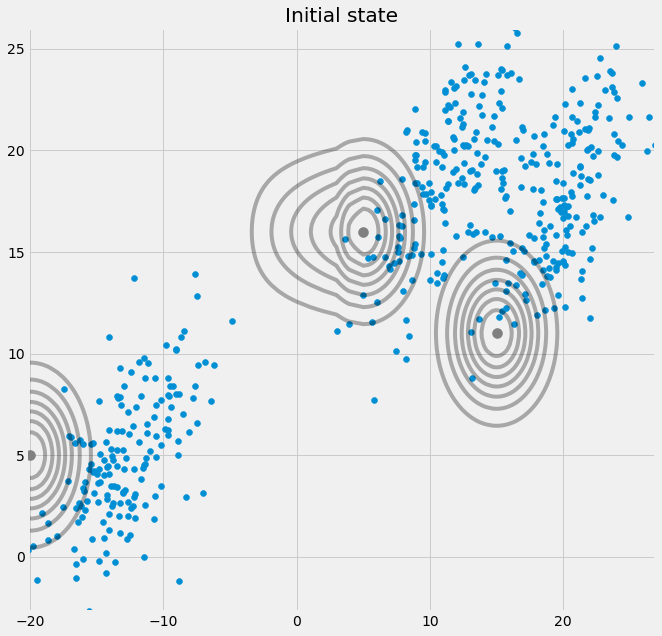
ax0.set_title('Initial state')
for m,c in zip(self.mu,self.cov):
c += self.reg_cov
multi_normal = multivariate_normal(mean=m,cov=c)
ax0.contour(np.sort(self.X[:,0]),np.sort(self.X[:,1]),multi_normal.pdf(self.XY).reshape(len(self.X),len(self.X)),colors='black',alpha=0.3)
ax0.scatter(m[0],m[1],c='grey',zorder=10,s=100)
for i in range(self.iterations):
r_ic = np.zeros((len(self.X),len(self.cov)))
for m,co,p,r in zip(self.mu,self.cov,self.pi,range(len(r_ic[0]))):
co+=self.reg_cov
mn = multivariate_normal(mean=m,cov=co)
r_ic[:,r] = p*mn.pdf(self.X)/np.sum([pi_c*multivariate_normal(mean=mu_c,cov=cov_c).pdf(X) for pi_c,mu_c,cov_c in zip(self.pi,self.mu,self.cov+self.reg_cov)],axis=0)
self.mu = []
self.cov = []
self.pi = []
log_likelihood = []
for c in range(len(r_ic[0])):
m_c = np.sum(r_ic[:,c],axis=0)
mu_c = (1/m_c)*np.sum(self.X*r_ic[:,c].reshape(len(self.X),1),axis=0)
self.mu.append(mu_c)
self.cov.append(((1/m_c)*np.dot((np.array(r_ic[:,c]).reshape(len(self.X),1)*(self.X-mu_c)).T,(self.X-mu_c)))+self.reg_cov)
self.pi.append(m_c/np.sum(r_ic))
log_likelihoods.append(np.log(np.sum([k*multivariate_normal(self.mu[i],self.cov[j]).pdf(X) for k,i,j in zip(self.pi,range(len(self.mu)),range(len(self.cov)))])))
fig2 = plt.figure(figsize=(10,10))
ax1 = fig2.add_subplot(111)
ax1.set_title('Log-Likelihood')
ax1.plot(range(0,self.iterations,1),log_likelihoods)
def predict(self,Y):
fig3 = plt.figure(figsize=(10,10))
ax2 = fig3.add_subplot(111)
ax2.scatter(self.X[:,0],self.X[:,1])
for m,c in zip(self.mu,self.cov):
multi_normal = multivariate_normal(mean=m,cov=c)
ax2.contour(np.sort(self.X[:,0]),np.sort(self.X[:,1]),multi_normal.pdf(self.XY).reshape(len(self.X),len(self.X)),colors='black',alpha=0.3)
ax2.scatter(m[0],m[1],c='grey',zorder=10,s=100)
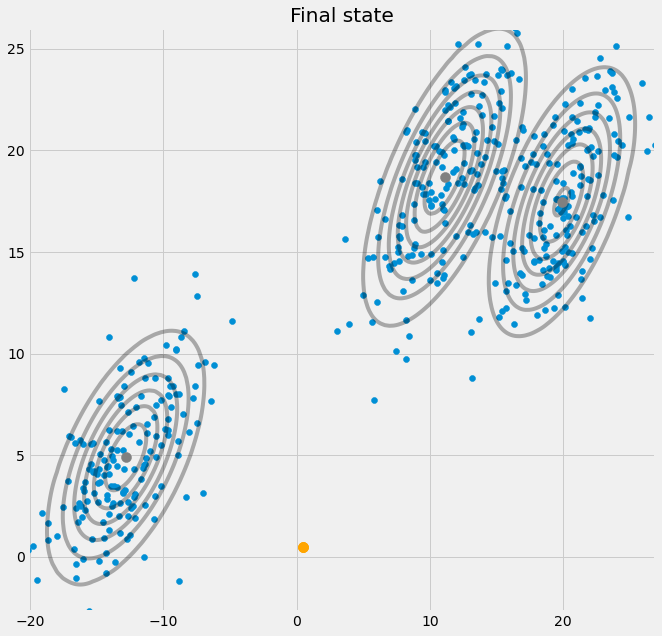
ax2.set_title('Final state')
for y in Y:
ax2.scatter(y[0],y[1],c='orange',zorder=10,s=100)
prediction = []
for m,c in zip(self.mu,self.cov):
prediction.append(multivariate_normal(mean=m,cov=c).pdf(Y)/np.sum([multivariate_normal(mean=mean,cov=cov).pdf(Y) for mean,cov in zip(self.mu,self.cov)]))
return prediction
GMM = GMM(X, 3, 50)
GMM.run()
GMM.predict([[0.5, 0.5]])
原始状态:
EM优化后:
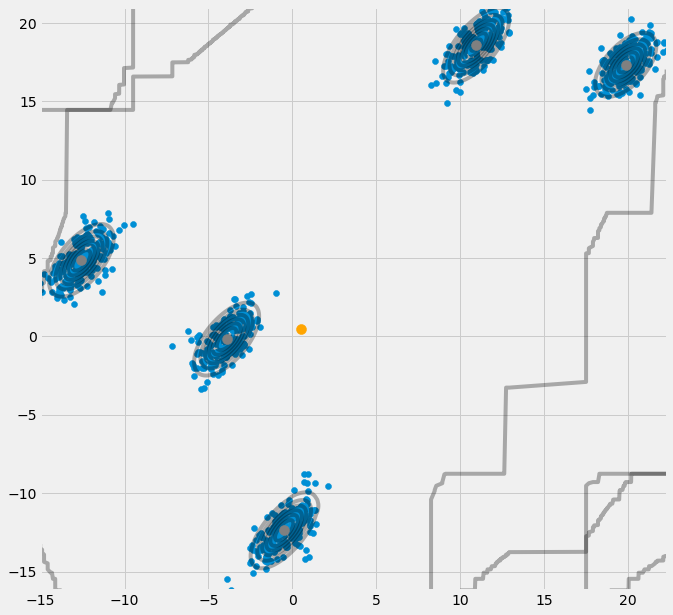
五个组别的也一样可以收敛的很到位:
4. 讨论
EM算法广泛应用于许多领域,尤其在统计学、机器学习和数据挖掘中,用于处理包含缺失数据或未观测变量的复杂模型,如高斯混合模型(GMM)、隐马尔可夫模型(HMM)等。通过EM算法,我们可以估计模型参数,对数据进行聚类、密度估计等任务,从而更好地理解和分析数据。
常见的机器学习算法实战演示基本上都在前10节归纳到位了,从本节起也会陆续把重心放到优化算法上。