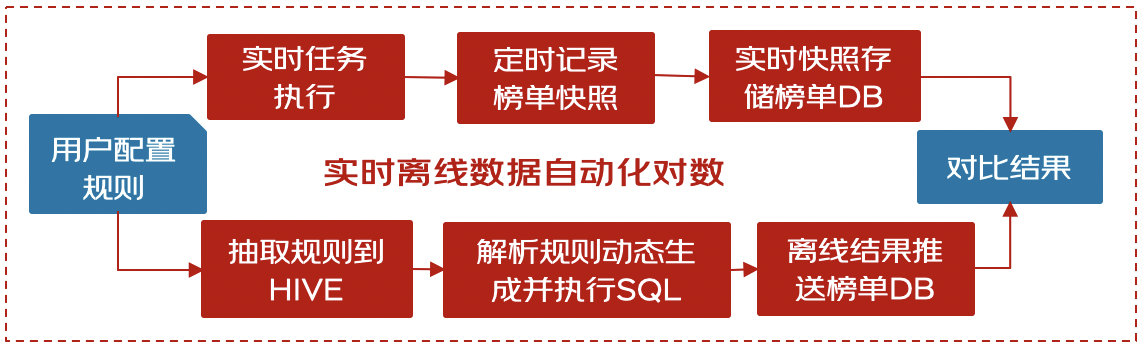
总结

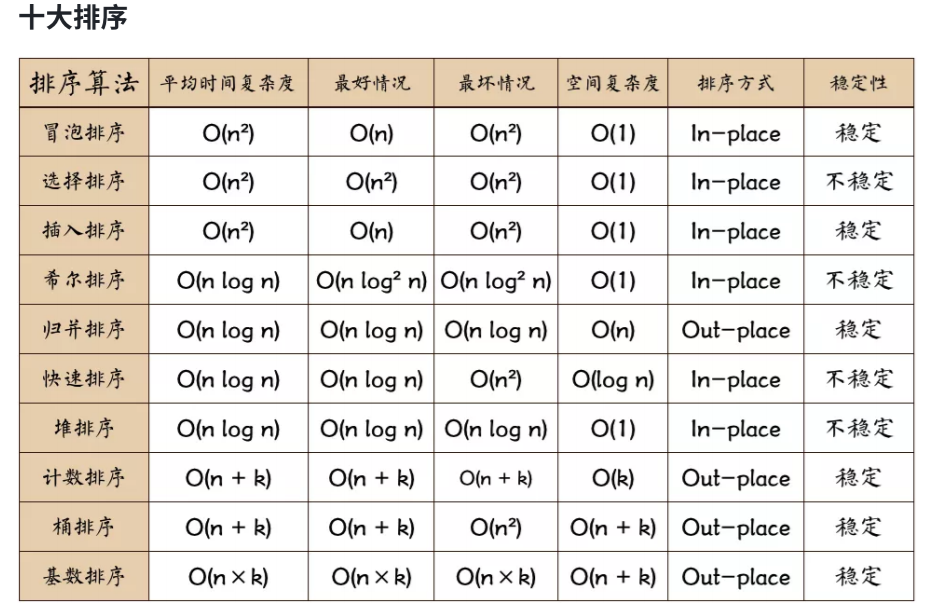
为什么需要稳定排序？

▪ 让第⼀个关键字的排序结果服务于第⼆个关键字排序中数值相同的那些数

▪ 主要是为了第⼀次考试分数相同时候，可以按照第⼆次分数的⾼低进行排序 

 一、冒泡排序

从最简单的冒泡排序开始

思想：交换相邻的元素，每次把最大的放在最后

vector<int> bubble_sort(vector<int>& arr) {
    for (int i = 0; i < arr.size(); ++i) {
        bool flag = false;
        for (int j = 0; j < n - i -1; ++j) {
            if (arr[j] > arr[j+1]) {
                swap(arr[j], arr[j+1]);
                flag = true;
            }             
        }
        if (flag == false) break;
    }
    return arr;
}

• 稳定排序、原地排序

• 最好O(n)、最差O(n^2)

• 拓展

        a. 优化：代码中的flag，如果数组整个已经有序，数组有序就退出

        b. 再优化：后半部分可能已经有序，每次可以更新j循环的右边界        

        c. 使用递归实现冒泡排序

        d. 使用两个栈实现冒泡排序

        e. 对链表进行冒泡排序（交换值or交换节点）  

        拓展可看冒泡排序

二、选择排序

思想：选⼀个最小的和前面的交换

vector<int> insertionSort(vector<int> arr) {
    if(arr.size() == 0) return arr;
    for (int i = 0; i < arr.size(); i++){
        int min = i;
        for (int j = i + 1; j < arr.size(); j++) {
            if(arr[j] < arr[min]) min = j;
        }
        swap(arr[i], arr[min]);
    }
    return arr;
}

 

三、快速排序

void quick_sort(int q[], int l, int r)  //stl源码剖析中快速排序差不多就是用的这种双指针
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j) {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i < j) {
            swap(q[i], q[j]);
        }
    }
    quick_sort(q, l, j);
    quick_sort(q, j+1, r);
}

 

 

四、归并排序

void merge_sort(int q[],int l, int r) //用到分治的思想。
{      
    if(l >= r) return;
    int mid = l + r >> 1;
    vector<int> tmp(r - l + 1, 0);
    merge_sort(q, l, mid);
    merge_sort(q, mid+1, r);
    int i = l, j = mid + 1, k=0;
    while (i <= mid && j <= r) {
        if (q[i]<=q[j]) tmp[k++] = q[i++];
        else  tmp[k++] = q[j++];   //tmp数组在全局定义；
    }
    while(i <= mid)  tmp[k++] = q[i++];
    while(j <= r)  tmp[k++] = q[j++];  
    for (int i = l, j = 0; i <= r; i++,j++)
    {
        q[i] = tmp[j];
    }
}