第四章 No.2单点线段树的介绍与使用

文章目录

- 基本操作
- 练习题
- - 1275. 最大数
  - 245. 你能回答这些问题吗
  - 246. 区间最大公约数

基本操作

单点线段树一共4个常用操作，pushup, build, modify, query
相比区间线段树少了pushdown，懒标记，由于pushdown的实现极容易SF，所以能用单点线段树就不用用区间线段树

单点线段树和区间线段树是我自己的叫法，当线段树只支持修改任意点的操作时，我称它为单点线段树。当线段树支持修改整个区间时，我称它为区间线段树

线段树的空间问题，要开多少空间？若线段长度为 $n$ ，一般开 $4 n$ 的空间

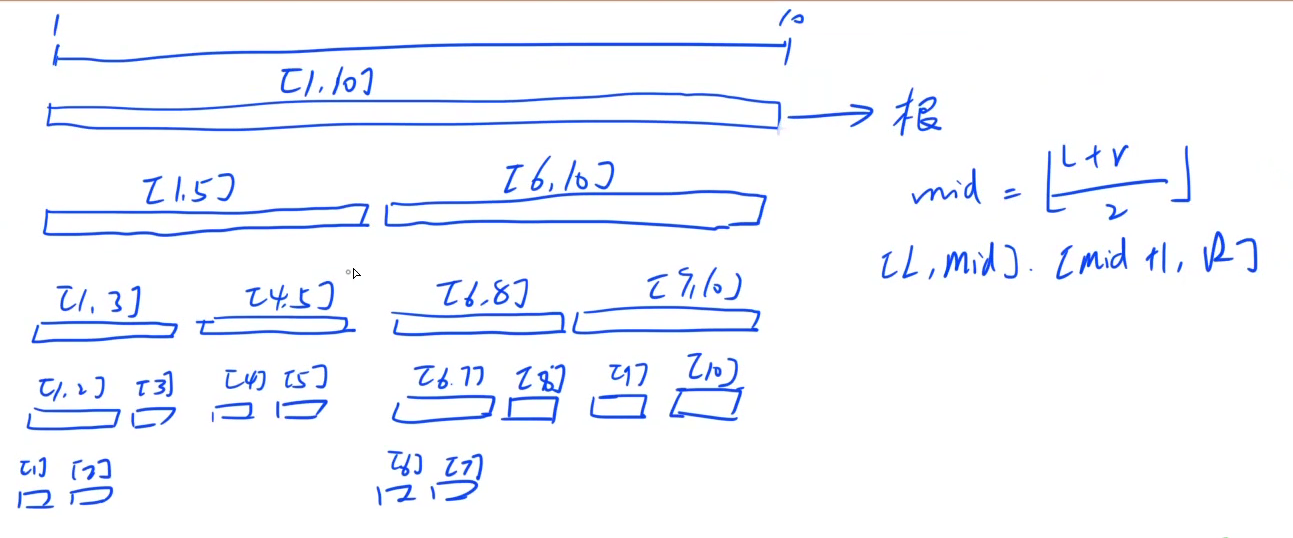
除了最后一层，剩下的是一个满二叉树

四个操作介绍：
void pushup(int u)：合并线段的操作，根据子节点的信息，维护更新父节点的信息
void build(int u, int l, int r)：建立一个 $[l, r]$ 区间，u是区间在树中对应的唯一下标
void modify(int u, int x, int v)：修改区间 $[x, x]$ 的属性为v，其中u是当前区间在树中对应的唯一下标
void query(int u, int l, int r)：查询区间 $[l, r]$ 在树中的信息
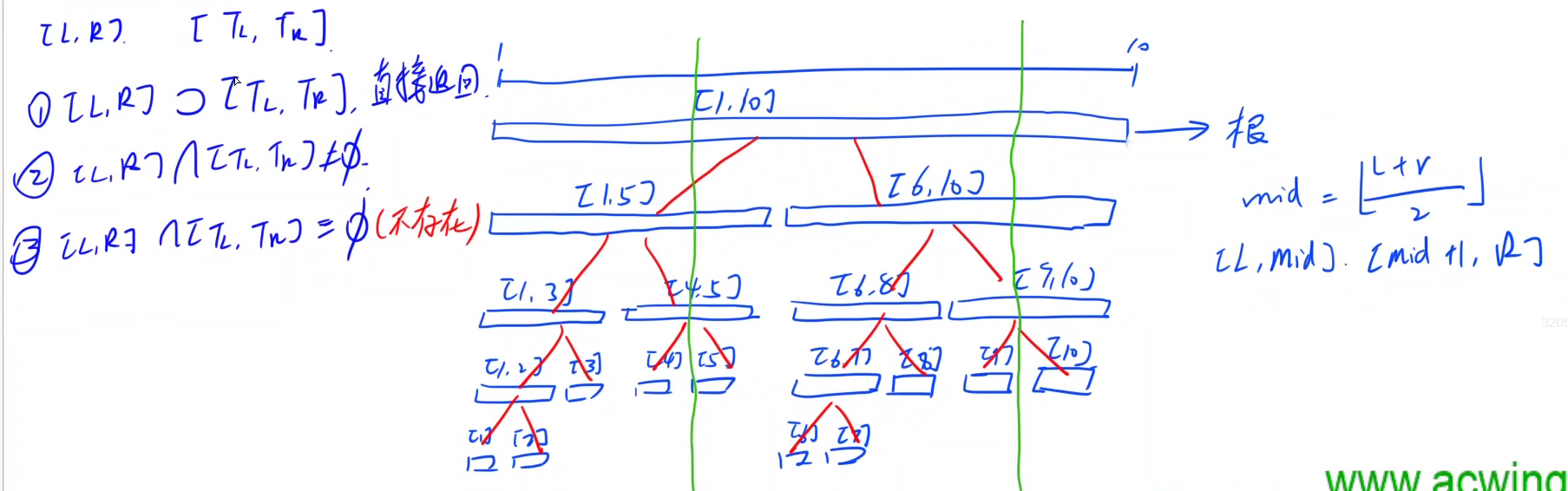
分三种情况：

当前节点u表示的线段 $[tl, t r]$ 是查询区间 $[l, r]$ 的子集，此时直接返回当前区间的信息
当前节点u表示的线段 $[tl, t r]$ 不是查询区间 $[l, r]$ 的子集，但是两者有交集，根据 $[tl, t r]$ 的中点 $mi d$ 可以分成两种情况

$l <= mi d$ ，说明查询区间与当前区间的左半段有交集，需要查询 $[tl, mi d]$ ，也就是当前节点的左孩子
$r > mi d$ ，说明查询区间与当前区间的右半段有交集，需要查询 $[mi d + 1, t r]$ ，也就是当前节点的右孩子

至于说会存在当前区间与查询区间完全没有交集的情况吗？
只要保证查询区间与根节点表示的区间有交集，由于我们每次递归查询的时候，只会选择有交集的区间进行递归，没有交集的区间就不会选择，所以每次判断的时候不会遇到当前区间与查询区间没有交集的情况

当前节点的下标用u表示，那么左孩子的下标为 $u << 1$ ，右孩子的下标为 $1\ |\ 1$

其中需要说明的是build操作，build建立的线段树是静态的，也就是说我们要提前知道线段的长度才能用build开出线段树
build将所有节点的信息初始化为空，再根据题目给定的信息调用modify修改空节点，以此做为线段树的初始化

build操作的实现：

void bulid(int u, int l, int r)
{
	tr[i] = { l, r };
	if (l == r) return;
	int mid = l + r >> 1;
	build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

递归实现bulid，第一个参数 $u$ 作为递归参数，表示节点的编号， $l$ 和 $r$ 表示当前区间的左右端点
build将在树中建立一个 $[l, r]$ 区间，若l != r说明当前建立的区间不是树的叶子节点，需要二分 $l$ 和 $r$ ，然后继续往下建立区间。直到l == r停止，当前节点为叶节点，无法继续建立区间

modify操作的实现：

void modify(int u, int x, int v)
{
	if (tr[u].l == x && tr[u].r == x) tr[u].v = v;
	else
	{
		int mid = tr[u].l + tr[u].r >> 1;
		if (x <= mid) modify(u << 1, x, v);
		else modify(u << 1 | 1, x, v);
		pushup(u); // 节点信息的维护
	}
}

同样，u是递归参数，x为需要修改的区间。由于是单点线段树，所以只支持修改“一个点”的操作，即l == r == x
若当前节点u表示的区间不是 $[x, x]$ ，那么二分区间向下递归查找目标区间。注意，修改完节点信息后，需要进行pushup维护，向上修改所有包含x的区间信息

query操作的实现：

int query(int u, int l, int r)
{
	if (l <= tr[u].l && tr[u].r <= r) return tr[u].v;
	int mid = trr[u].l + tr[u].r >> 1;
	int v = 0;
	if (l <= mid) v = query(u << 1, l, r);
	if (r > mid) v = max(v, query(u << 1 | 1, l, r));
	return v;
}

同样，u是递归参数，query将查找区间 $[l, r]$ 的信息，之前已经介绍过query的三种情况，这里不再赘述

pushup操作需要结合题目具体实现

练习题

1275. 最大数

1275. 最大数 - AcWing题库

板子题，题意很直白，需要实现两个操作：1. 在任意位置（序列最后）添加一个数，对应modify操作 2. 询问某段区间的最大值，对应query操作
思考节点需要维护什么信息才能支持query（区间最大值）操作？很显然，当前区间 $[l, r]$ 的最大值一定要维护。那么 $[l, r]$ 的最大值是否能通过子区间的信息推导出来，显然一个max就能搞定

所以一顿分析后，我们知道节点只需要存储 $[l, r]$ 与最大值即可，pushup将基于两子区间推导当前区间的最大值

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 2e5 + 10;
struct Node
{
    int l, r;
    int v; // 表示当前区间的最大值
}tr[4 * N];

void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

void build(int u, int l, int r)
{
    tr[u] = { l, r };
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

int query(int u, int l, int r)
{
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].v;
    int mid = (tr[u].l + tr[u].r) >> 1;
    int v = 0;
    if (l <= mid) v = query(u << 1, l, r);
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

int main()
{
    int m, p;
    scanf("%d%d", &m, &p);
    int n = 0; // 表示线段的数量
    build(1, 1, m);
    int a = 0, x;
    char op[2];
    while (m -- )
    {
        scanf("%s%d", op, &x);
        if (op[0] == 'A')
            modify(1, ++ n, ((LL)a + x) % p);
        else
        {
            a = query(1, n - x + 1, n);
            printf("%d\n", a);
        }
    }
    return 0;
}

debug：query的int v = 0必须初始化
因为第一个if不一定进去，v的值不一定能被该if初始化
所以在第二个if时，v的随机值可能影响最后的max取值

245. 你能回答这些问题吗

245. 你能回答这些问题吗 - AcWing题库

裸题，实现两个操作：1. 单点修改 2. 区间的最大连续子段和
一般问题的最大连续子段和可以用dp与类似归并排序的递归解，显然这题不能用dp，所以这里借用归并的思想
将当前区间 $[l, r]$ 分成两个子区间，当前区间的最大连续子段和有三种情况

左子区间的最大连续子段和
右子区间的最大连续子段和
左子区间的最大后缀和加上右子区间的最大前缀和

在三者中取max即可。所以线段树的节点需要维护三个信息：1. 最大连续子段和 2. 最大前缀和 3. 最大后缀和
当前区间的前缀和要如何维护？有两种情况：1. 左子区间的最大前缀和 2. 左子区间和加上右子区间的最大前缀和，当前区间的最大后缀和也是同理，所以节点还需要维护当前区间和这一信息

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 5e5 + 10;
int a[N];
struct Node
{
    int l, r;
    LL sum, lm, rm, tm;
}tr[4 * N];

void pushup(Node &u, Node &l, Node &r)
{
    u.sum = l.sum + r.sum;
    u.lm = max(l.lm, l.sum + r.lm);
    u.rm = max(r.rm, r.sum + l.rm);
    u.tm = max(max(l.tm, r.tm), l.rm + r.lm);
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = { l, r, a[l], a[l], a[l], a[l] };
    else
    {
        tr[u] = { l, r };
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
    }
}

void modify(int u, int x, LL v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u] = { x, x, v, v, v, v };
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

Node query(int u, int l, int r)
{
    if (l <= tr[u].l && tr[u].r <= r) return tr[u];
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return query(u << 1, l, r);
        else if (l > mid) return query(u << 1 | 1, l, r);
        else
        {
            Node res;
            Node left = query(u << 1, l, r);
            Node right = query(u << 1 | 1, l, r);
            pushup(res, left, right);
            return res;
        }
    }
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]);
    build(1, 1, n);
    int t, x, y;
    while (m -- )
    {
        scanf("%d%d%d", &t, &x, &y);
        if (t == 1)
        {
            if (x > y) swap(x, y);
            printf("%lld\n", query(1, x, y).tm);
        }
        else
        {
            modify(1, x, y);
        }
    }
    return 0;
}

其中，pushup被设置为重载，这是因为有些函数会使用pushup(int u)，有些函数会使用pushup(Node &u, Node &l, Node &r)
与第一题的板子不同，这一题的板子中。build函数使用了pushup的第一个重载，因为题目已经给定了指定的数用来初始化线段树，而第一题没有给定数据，所以只能先建空树

query也使用了pushup，并且else部分与第一题不同
由于第一题查询的是区间最大值，所以二分当前区间后，查出左子区间的最大值与右子区间的最大值再取个max即可
但是这题要查询的是最大连续子段和，不能从左右子区间的最大连续子段和推出当前区间的最大连续字段和，因为还有一种情况存在：左子区间的最大后缀+右子区间的最大前缀
所以这里要判断三种情况：

r <= mid，查询区间 $[l, r]$ 完全在当前区间的左子区间
l > mid，查询区间 $[l, r]$ 完全在当前区间的右子区间
查询区间 $[l, r]$ 不仅在当前区间的左子区间还在当前区间的右子区间，此时要调用pushup，整合两个子区间的信息，将这些信息保存到Node中

246. 区间最大公约数

246. 区间最大公约数 - AcWing题库

整个区间加上或者减去一个数，不涉及“修改整个区间的值”，自然想到差分数组，可以用节点维护差分信息，即 $a [i] - a [i - 1]$
由于要求区间的最大公约数，所以至少要维护”区间的最大公约数“的信息
接着思考区间 $[l, r]$ 的最大公约数是否能通过子区间的最大公约数得到？若是不能则需要维护其他信息
假设当前区间被分为左右两个区间，左区间最大公约数为 $a$ ，右区间最大公约数为 $b$
显然，由于求当前区间的最大公约数只会用到 $a$ 和 $b$ ，所以节点就不用额外维护其他信息

当区间维护着差分信息，如何求其的最大公约数？

由性质d | a && d | b -> d | ax + by，所以
求 $a_1, a_2, ..., a_n$ 的最大公约数，等同于求 $a_1, a_2-a_1, ..., a_n-a_{n-1}$ 的最大公约数
后n-1个数是节点保存的差分信息，求这些数： $a_2-a_1, ..., a_n-a_{n-1}$ 的最大公约数，可以直接用节点维护的差分信息
但是第1个数是个前缀和信息，节点只保存差分信息不够，还要维护sum信息以求前缀和得到区间的第一个数 $a_l$

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 5e5 + 10;

LL w[N];

struct Node
{
    int l, r;
    LL d, sum;
}tr[N * 4];

LL gcd(LL a, LL b)
{
    return b ? gcd(b, a % b) : a;
}

void pushup(Node &u, Node &l, Node &r)
{
    u.d = gcd(l.d, r.d);
    u.sum = l.sum + r.sum;
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r)
{
    if (l== r) 
    {
        LL t = w[l] - w[l - 1];
        tr[u] = { l, r, t, t };
    }
    else
    {
        tr[u] = { l, r };
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int x, LL v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u].sum += v, tr[u].d += v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

Node query(int u, int l, int r)
{
    if (l <= tr[u].l && tr[u].r <= r) return tr[u];
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return query(u << 1, l, r);
        else if (l > mid) return query(u << 1 | 1, l, r);
        else
        {
            auto left = query(u << 1, l, r);
            auto right = query(u << 1 | 1, l, r);
            Node res;
            pushup(res, left, right);
            return res;
        }
    }
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i ) scanf("%lld", &w[i]);
    build(1, 1, n);
    
    char op[2]; int l, r;
    LL t;
    while (m -- )
    {
        scanf("%s%d%d", op, &l, &r);
        if (op[0] == 'Q')
        {
            if (l == r) printf("%lld\n", query(1, 1, l).sum);
            else
            {
                LL a = query(1, 1, l).sum;
                printf("%lld\n", abs(gcd(a, query(1, l + 1, r).d)));
            }
        }
        else
        {
            scanf("%lld", &t);
            modify(1, l, t);
            if (r + 1 <= n) modify(1, r + 1, -t);
        }
    }
    return 0;
}

debug：if (l == r) printf("%lld\n", query(1, 1, l).sum)当查询单点最大公约数时，需要返回这个点上的数，由于保存的时差分信息所以需要求一个前缀和
之前写成if (l == r) printf("%lld\n", query(1, l, r).d)，乐
题目没想清楚就写题，真的会debug到死