0.知识回顾

描述旋转本身的矩阵叫做旋转矩阵，旋转矩阵是一个行列式为1的正交矩阵 ，反之，行列式为1的正交矩阵也是一个旋转矩阵。将n维旋转矩阵的集合定义如下：
S O ( n ) = { R ∈ R n ∗ n ∣ R R T = I ， d e t ( R ) = 1 } SO(n)=\{R\in \mathbb{R}^{n*n}|RR^T=I，det(R)=1\} SO(n)={R∈Rn∗n∣RRT=I，det(R)=1}
SO(n)是特殊正交群。

我们把旋转和平移写在一个矩阵T里，将其变成四维向量，成为齐次坐标，矩阵T称为变换矩阵。对于变换矩阵，它具有比较特别的结构，左上角为旋转矩阵，右侧为平移向量，左下角为0向量，右下角为1。这种矩阵为特殊欧式群。
S E ( 3 ) = { T = [ R t 0 1 ] ∈ R 4 ∗ 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } SE(3)=\{T=\left[ \begin{matrix} R & t\\ 0& 1 \end{matrix} \right]\in \mathbb{R}^{4*4} |R\in SO(3),t\in \mathbb{R}^{3}\} SE(3)={T=[R0​t1​]∈R4∗4∣R∈SO(3),t∈R3}
在旋转矩阵或者变换矩阵中，它们是对加法不封闭的，就是说，对于任意两个旋转矩阵$R_1$、$R_2$，按照矩阵加法的定义，和不再是一个旋转矩阵。但是乘法对应着旋转或者变换的复合，两个旋转矩阵相乘表示做了两次旋转。对于这种只有一个运算的集合，我们称之为群。

1.群

群是一种集合加上一种运算的代数结构，我们把集合记作A，运算记作 · ，那么群可以记作G=（A,·）。

1.1 李群

李群是指具有连续（光滑）性质的群，SO(n)和SE(n)在实数空间上是连续的，我们可以直观地想象一个刚体能够连续地在空间中运动，所以它们是李群。

1.2 李代数引出

考虑任意旋转矩阵R，我们知道它满足：
$$R{R}^T=I$$
现在，R是某个相机的旋转，他会随时间连续地变化，即为时间的函数:R(t)。由于他仍是旋转矩阵，有：
$$R(t)R(t{)}^T=I$$
在等式两边对时间求导，得到：
$$\dot{R}(t)R(t{)}^T+R(t)\dot{R}(t{)}^T=0$$
整理得：
$$\dot{R}(t)R(t{)}^T=-(R(t)\dot{R}(t{)}^T{)}^T$$
可以看出$\dot{R}(t)R(t{)}^T$是一个反对称矩阵，即满足$A^T=-A$。

这里引入一个^符号，将一个向量变成了反对称矩阵，同理，对于任意反对称矩阵，我们也能找到唯一与之对应的向量，用符号v表示。
$$a^{\wedge }=A=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right],A^{\vee }=a$$
于是，由于$\dot{R}(t)R(t{)}^T$是个反对称矩阵，我们可以找到一个三维向量$\varphi (t)\in {\mathbb{R}}^3$与之对应：
$$\dot{R}(t)R(t{)}^T=\varphi (t{)}^{\wedge }$$
等式两边右乘R(t)，由于R为正交矩阵，有：
$$\dot{R}(t)R(t)=\varphi (t{)}^{\wedge }R(t)=\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ {\varphi }_3& 0& -{\varphi }_1\\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]R(t)$$
可以看到，每对旋转矩阵求一次导数，只需左乘一个$\varphi (t)$矩阵即可，考虑$t_0=0$时，设此时旋转矩阵为$R(0)=I$。按照导数定义，可以把$R(t)$在t=0附近进行一阶泰勒展开：
$$\begin{gathered} R(t)=R(t_0)+\dot{R}(t_0)(t-t_0) \\ =I+\varphi (t{)}^{\wedge }(t) \end{gathered}$$
我们看到$\varphi$反应了R的导数性质，故称他在SO(3)原点附近的正切空间上，同时在$t_0$附近，设$\varphi (t_0)={\varphi }_0$。那么有：
$$\dot{R}(t)=\varphi (t{)}^{\wedge }R(t)={\varphi }_0^{\wedge }R(t)$$
上式是一个关于R的微分方程，而且有初始值$R(0)=I$，解得：
$$R(t)=exp({\varphi }_{0}t)$$
以上式子说明在t=0附近，旋转矩阵可以由$exp({\varphi }_{0}t)$计算出来。

可以说明下面两个关系：

1.给定某时刻的R，我们能求得一个$\varphi$，它描述了R在局部的导数关系，$\varphi$正是对应到SO(3)上的李代数so(3)。

2.给定某个向量$\varphi$，矩阵指数$exp({\varphi }_{0}t)$的计算就是李群和李代数间的指数/对数映射。

1.3 李代数的意义

1.应用意义

在视觉slam中，我们需要不断计算相机的位姿和构建地图，相机的位姿表现在其变换矩阵T，由于干扰的存在，我们无法准确获得所需要的信息，所以我们转而求其最小误差。

假设我们有N个三维点p和对应的观测值z，我们的目标就是寻找一个最佳位姿T，使得整体误差最小化，如下式：
$$\underset{T}{\min }J(T)=\sum _{i=1}^N||z_i-T{p}_i|{|}_2^2$$
要求解上面的方程，就是要求目标函数J对T的导数，但是由于T所在的变换矩阵群（SO(3)）对加法不封闭，无法直接求取，所以我们需要引入一个新的量，通过对该量的计算间接获得对T的求导，这个引入的量就是李代数

2.数学意义

每个李群都有与之对应的李代数。李代数描述了李群的局部性质（局部导数），准确的说是单位元附近的正切空间。

1.4 李代数定义

李代数有一个集合$\mathbb{V}$、一个数域$\mathbb{F}$和一个二元运算[，]组成，如果满足以下几条性质，则称（$\mathbb{V}$，$\mathbb{F}$，[，]）为一个李代数，记作g。

1.封闭性 $\forall X,Y\in \mathbb{V},[X,Y]\in \mathbb{V}$

2.双线性 $\forall X,Y,Z\in \mathbb{V},a,b\in \mathbb{F}$ 有 [aX+bY,Z]=a[X,Z]+b[Y,Z]，[Z,aX+bY]=a[Z,X]+b[Z,Y]

3.自反性 $\forall X\in \mathbb{V},[X,X]=0$

4.雅克比等价 $\forall X,Y,Z\in \mathbb{V}$ [X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0

相比于群中较为简单为二元运算，李括号[,]表达了两个元素的差异。

1.5 李代数so(3)

之前提到的$\varphi$，事实上就是一种李代数。SO(3)对应的李代数就是定义在${\mathbb{R}}^3$上的向量，我们记作$\Phi$
s o ( 3 ) = { ϕ ∈ R 3 , Φ = ϕ 0 ∧ ∈ R 3 ∗ 3 } so(3)=\{\phi\in \mathbb{R}^{3},\Phi=\phi_0^ \wedge \in \mathbb{R}^{3*3}\} so(3)={ϕ∈R3,Φ=ϕ0∧​∈R3∗3}
so(3)是由三维向量组成的集合，每个向量对应一个反对称矩阵，可以用于表达旋转矩阵的导数。他与SO(3)的关系有指数映射给定:
$$R(t)=exp({\varphi }_{0}t)$$

1.6 SO(3)上的指数映射

这个问题就是如何计算$exp({\varphi }_{0}t)$

任意矩阵的指数映射可以写成一个泰勒展开，但是之后只有在收敛的情况下才会有结果，其结果仍是一个矩阵：
$$exp(A)=\sum _{n=0}^{\infty }\frac{1}{n!}{A}^n$$
带入${\varphi }^{\wedge }$，得到:
$$exp({\varphi }^{\wedge })=\sum _{n=0}^{\infty }\frac{1}{n!}{{\varphi }_0^{\wedge }}^n$$
但是上式无法直接计算，因为需要计算矩阵的无穷次幂。下面进行一种简单的方法。

由于$\varphi$是三维向量，可以定义他的模长和方向，分别记作$\theta$和a。这里$\varphi =\theta a$，a为一个长度为1的方向向量。对于$a^{\wedge }$有以下性质：
$$a^{\wedge }{a}^{\wedge }=\left[\begin{array}{ccc}-a_2^2-a_3^2& a_1{a}_2& a_1{a}_3\\ a_1{a}_2& -a_1^2-a_3^2& a_2{a}_3\\ a_1{a}_3& a_2{a}_3& -a_1^2-a_2^2\end{array}\right]=a{a}^T-I$$

$$a^{\wedge }{a}^{\wedge }{a}^{\wedge }=a^{\wedge }(a{a}^T-I)=-a^{\wedge }$$

上面两个式子提供了处理$a^{\wedge }$高阶项的方法，这样可以把指数映射写成：
$$\begin{gathered} exp({\varphi }^{\wedge })=exp(\theta a^{\wedge })=\sum _{n=0}^{\infty }\frac{1}{n!}(\theta a^{\wedge }{)}^n \\ =I+\theta a^{\wedge }+\frac{1}{2!}{\theta }^2{a}^{\wedge }{a}^{\wedge }+\frac{1}{3!}{\theta }^3{a}^{\wedge }{a}^{\wedge }{a}^{\wedge }\cdots \\ =a{a}^T-a^{\wedge }{a}^{\wedge }+\theta a^{\wedge }+\frac{1}{2!}{\theta }^2{a}^{\wedge }{a}^{\wedge }-\frac{1}{3!}{\theta }^3{a}^{\wedge }\cdots \\ =a{a}^T+(\theta -\frac{1}{3!}{\theta }^3+\frac{1}{5!}{\theta }^5-\cdots )a^{\wedge }-(1-\frac{1}{2!}{\theta }^2+\frac{1}{4!}{\theta }^4-\cdots )a^{\wedge }{a}^{\wedge } \\ =a^{\wedge }{a}^{\wedge }+I+sin\theta a^{\wedge }-cos\theta a^{\wedge }{a}^{\wedge } \\ =(1-cos\theta )a^{\wedge }{a}^{\wedge }+I+sin\theta a^{\wedge } \\ =cos\theta I+(1-cos\theta )a{a}^T+sin\theta a^{\wedge } \end{gathered}$$

经过以上计算，得到：
$$exp({\varphi }^{\wedge })=cos\theta I+(1-cos\theta )a{a}^T+sin\theta a^{\wedge }$$
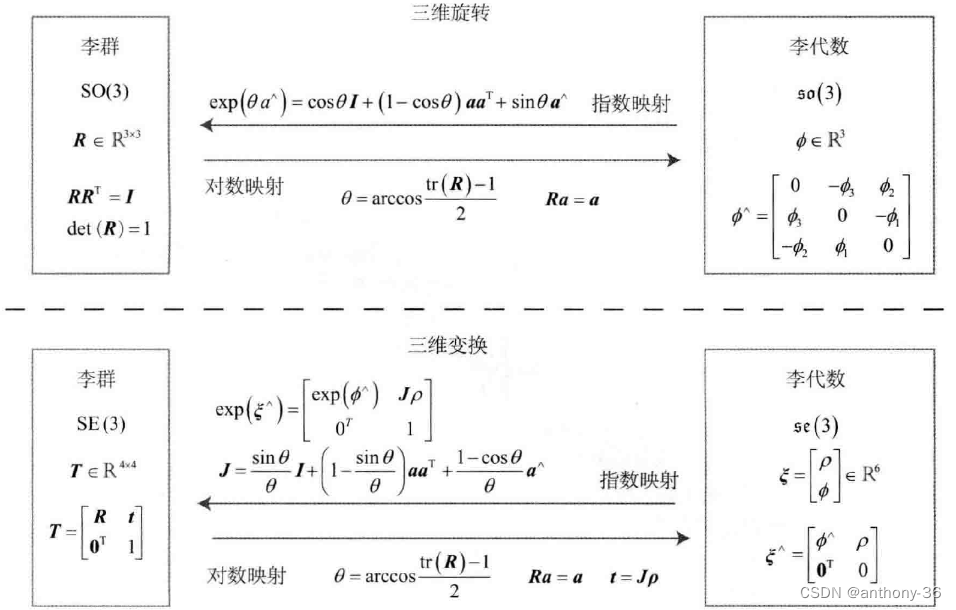
可以发现上式就是罗德里格斯公式，so(3)就是由所谓的旋转向量组成的空间，指数映射即罗德里格斯公式，通过这个公式，我们把任意一个向量对应到一个位于SO(3)中的旋转矩阵。

罗德里格斯公式就是表明旋转向量到旋转矩阵的转换过程。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6dVI3FiO-1690698811035)(C:\Users\13611\AppData\Roaming\Typora\typora-user-images\image-20230730143034186.png)]

本文主要参考《视觉SLAM十四讲》
以发现上式就是罗德里格斯公式，so(3)就是由所谓的旋转向量组成的空间，指数映射即罗德里格斯公式，通过这个公式，我们把任意一个向量对应到一个位于SO(3)中的旋转矩阵。

罗德里格斯公式就是表明旋转向量到旋转矩阵的转换过程。

本文主要参考《视觉SLAM十四讲》