原文链接:https://mp.weixin.qq.com/s?__biz=Mzg4MjgxMjgyMg==&mid=2247486540&idx=1&sn=6ebd9f58e9f08a369904f9c48e12d136&chksm=cf51beb5f82637a3c65cf6fa53e8aa136021e35f63a58fdd7154fc486a285ecde8b8521fa499#rd
ICASSP 2023 | Cough Detection Using Millimeter-Wave FMCW Radar
毫米波感知论文阅读 | ICASSP 2023, Cough Detection Using Millimeter-Wave FMCW Radar

Abstract
-
研究内容
-
提出了一种使用毫米波FMCW雷达检测人体咳嗽信号的信号处理方法
✅ 利用FMCW雷达的相位解调技术可以提取咳嗽引起的微小振动
✅ 采用身体运动伪像消除(BMAC)技术可以抑制运动伪像 ⇒ \Rightarrow ⇒ (运动伪像可以轻易掩盖小振动)
✅ 即使存在大规模身体运动也可以测量咳嗽信号的振动频率
-
-
实验验证
-
进行了 仿真 来评估所提出方法检测咳嗽信号的概率和准确性
✅ 包括分析了FMCW线性调频非线性的影响
-
提出的技术还通过 60 GHz FMCW雷达进行了验证实验
-
-
贡献总结
-
首次使用FMCW雷达实现了咳嗽信号的检测
✅ 提出了身体运动伪像消除(BMAC)技术, 在存在身体运动的情况下检测咳嗽
-
通过仿真验证结果,分析了FMCW非线性性的影响
-
60GHz真实实验验证了所提出方法的有效性
-
1 Introduction
研究的背景和意义
- 传染病蔓延,对健康监测需求增长
- 毫米波雷达受关注,能远程监测生命体征
- 仅监测生命体征不足以判断呼吸状况
- 咳嗽是判断呼吸系统疾病的关键症状
毫米波咳嗽检测的挑战和问题
-
声音方法可侵犯隐私,受声学噪声影响
-
毫米波不受声学噪声影响,但研究很少
🚩 挑战:咳嗽带来大规模身体运动,运动伪像可压倒小振动
🚩 已有方法的不足 :仅检测咳嗽行为,不提取特征 + 未充分解决运动伪像问题
本文创新和贡献
- 检测包含大规模运动的咳嗽
- 提出身体运动伪像消除(BMAC)技术
- 通过仿真和实验进行了验证
2 Signal Model and Methodology
- 咳嗽信号的信号模型
- 使用FMCW雷达的检测方法
- 运动伪像消除技术
- 数值仿真
2.1. FMCW radar signal model
-
FMCW雷达的信号模型
- 在相干处理时间内发射M次脉冲
- 每个脉冲为FMCW线性调频信号
-
发射信号
- s T X ( t , m ) = 1 N c p ( t − m T p ) s_{TX}(t,m) = \frac{1}{\sqrt{N_c}}p(t-mT_p) sTX(t,m)=Nc1p(t−mTp)
- p ( t ) = e j ( 2 π f 0 t + π γ t 2 ) p(t)=e^{j(2\pi f_0t+\pi\gamma t^2)} p(t)=ej(2πf0t+πγt2)
- N c N_c Nc - 脉冲数, T p T_p Tp - 脉冲重复间隔
- γ \gamma γ - 频率斜率, f 0 f_0 f0 - 载波频率
-
接收信号
- s R X ( t , m ) = α s T X ( t − 2 ( d 0 + x [ m ] ) c , m ) + w c ( t , m ) s_{RX}(t,m) = \alpha s_{TX}(t-\frac{2(d_0+x[m])}{c},m) + w_c(t,m) sRX(t,m)=αsTX(t−c2(d0+x[m]),m)+wc(t,m)
- α \alpha α - 衰减系数, d 0 d_0 d0 - 初始距离
- x [ m ] x[m] x[m] - 目标运动, w c w_c wc - 噪声
-
离散后基带信号
- s b [ k , m ] = α e j 4 π c ( d 0 + x [ m ] ) ( f 0 + γ k ) + w c [ k , m ] s_b[k,m] = \alpha e^{j\frac{4\pi}{c}(d_0+x[m])(f_0+\gamma k)} + w_c[k,m] sb[k,m]=αejc4π(d0+x[m])(f0+γk)+wc[k,m]
- 用于后续检测分析
-
总结:建立了FMCW雷达的精确信号模型
- 包含线性调频发射信号
- 考虑了目标运动、距离、噪声等参数
2.2. Cough vibration and body motion artifacts
-
分析:目标运动的两种组成成分
- 咳嗽振动 v [ m ] v[m] v[m]
- 身体运动伪像 y [ m ] y[m] y[m]
-
咳嗽振动:
-
使用谐波模型表示
✅ v [ m ] = ∑ l = 1 L A v , l sin ( 2 π l f v m ) v[m] = \sum\limits_{l=1}^{L}A_{v,l}\sin(2\pi l f_vm) v[m]=l=1∑LAv,lsin(2πlfvm)
✅ L L L - 谐波数, A v , l A_{v,l} Av,l - 振幅, f v f_v fv - 基频
-
咳嗽振动特点
🚩 幅值较小(小于0.5mm)
🚩 频率范围80-240Hz
-
-
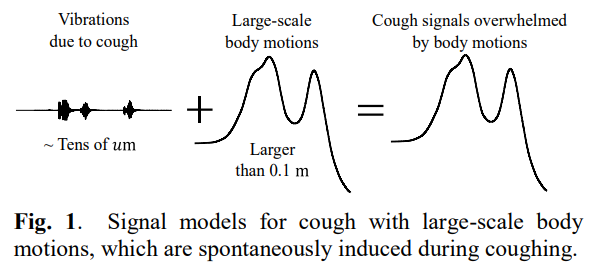
身体运动伪像: (特点)
- 幅值较大(大于0.1 m)
- 频谱从直流分量开始
-
两者的区别
- 幅值大小不同
- 频率范围不同
-
分析得到问题的关键
- 运动伪像会覆盖咳嗽振动
- 需要对两者进行区分
2.3. Signal processing method
-
目标 :
- 从接收信号中提取咳嗽振动 v [ m ] v[m] v[m]
-
挑战 :存在身体运动伪像
-
步骤1:估计身体运动的相位
- ϕ [ k , m ] = ∠ s b [ k , m ] = tan − 1 ( I m ( s b [ k , m ] ) R e ( s b [ k , m ] ) ) \phi[k,m] = \angle s_b[k,m] = \tan^{-1}\left(\frac{Im(s_b[k,m])}{Re(s_b[k,m])}\right) ϕ[k,m]=∠sb[k,m]=tan−1(Re(sb[k,m])Im(sb[k,m]))
-
步骤2:相位补偿消除身体运动
- ϕ ^ [ k , m ] = moving average of ϕ [ k , m ] \hat{\phi}[k,m] = \text{moving average of } \phi[k,m] ϕ^[k,m]=moving average of ϕ[k,m]
- h c = e − j ϕ ^ [ k , m ] h_c = e^{-j\hat{\phi}[k,m]} hc=e−jϕ^[k,m]
- s ^ b = s b ⊙ h c \hat{s}_b = s_b \odot h_c s^b=sb⊙hc
-
步骤3:FFT距离压缩
- s c [ m ] = F F T ( s ^ b [ ∗ , m ] ) s_c[m] = FFT(\hat{s}_b[*,m]) sc[m]=FFT(s^b[∗,m])
-
步骤4:FFT提取咳嗽频率
- S c [ l ] = F F T ( s c [ m ] ) S_c[l] = FFT(s_c[m]) Sc[l]=FFT(sc[m])
- f ^ v = arg max ∣ S c [ l ] ∣ \hat{f}_v = \arg\max |S_c[l]| f^v=argmax∣Sc[l]∣
总结:
关键技术 :
- 相位信息提取
- 相位补偿
- FFT范围压缩
处理流程 :
- 估计相位->补偿消除运动->FFT范围压缩->FFT提取频率
2.4. Effect of FMCW chirp non-linearity
-
FMCW线性调频信号可能存在非线性
-
非线性成分 :
- 周期性偏差: Δ f p = 2 π A p sin ( 2 π f p t ) \Delta f_p = 2\pi A_p\sin(2\pi f_pt) Δfp=2πApsin(2πfpt)
- 随机偏差: w f [ k ] ∼ N ( 0 , σ f 2 ) w_f[k] \sim \mathcal{N}(0,\sigma_f^2) wf[k]∼N(0,σf2)
-
线性调频带非线性 :
- f c h i r p [ k ] = γ k + f 0 + Δ f p + w f [ k ] f_{chirp}[k] = \gamma k + f_0 + \Delta f_p + w_f[k] fchirp[k]=γk+f0+Δfp+wf[k]
-
周期性偏差影响:
- 可通过相位补偿消除
- 不影响最终咳嗽检测
-
随机偏差影响:
- 导致相位估计错误
- 影响运动消除效果
- 降低咳嗽检测性能
3 Numerical Simulations
- 进行了数值模拟来评估和验证所提出的雷达系统检测咳嗽信号
- 使用了具有2 GHz带宽的FMCW线性调频脉冲
- 脉冲重复间隔(PRI)为2.5 kHz,相干积累间隔(CPI)为2秒
- 使用了0.25米位移的随机身体运动
- 为噪声模拟,进行了1000个样本的蒙特卡罗模拟
进行了3项仿真:
-
1 评估了根据振动幅度的检测概率随信噪比的变化
-
检测频率峰值的判据设定为5 dB
-
在没有身体运动的情况下,所需的SNR随振动检测线性减小:
S N R r e q ∝ A v SNR_{req} \propto A_{v} SNRreq∝Av
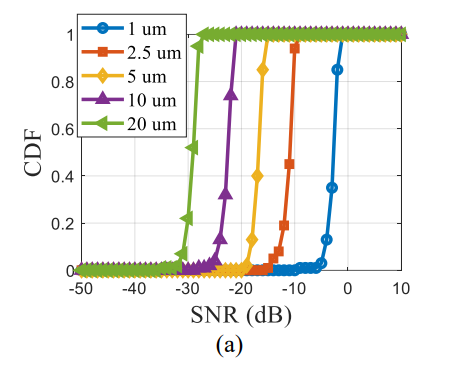
- 在存在身体运动的情况下,需要大于约-13 dB的较大SNR来检测20 um的振动幅度
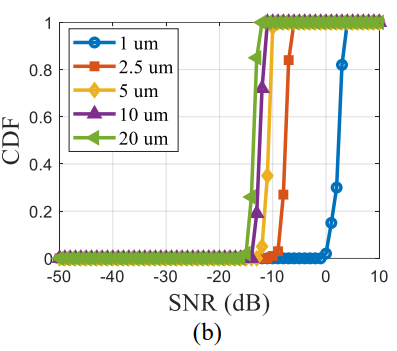
- 当振动幅度减小时,需要更大的信号功率来增加检测概率
- 作用:从模拟结果可以设计雷达系统规格及其覆盖范围以进行咳嗽检测
-
-
2 评估了检测10 um振动的振动频率的均方根误差(RMSE)随SNR的变化
- 如下图,没有使用BMAC时的RMSE远大于使用BMAC时的RMSE
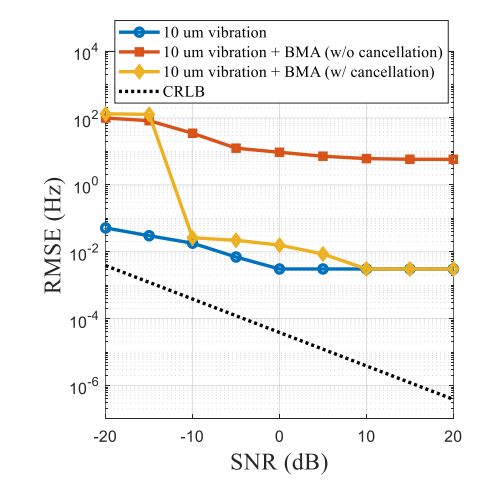
- 当SNR大于10 dB时,所提出的BMAC技术可以提供与没有身体运动情况下相同的检测精度
- 这里,周期性振动的Cramer-Rao下界简单计算为 C R L B ≈ 6 σ 2 π 2 E A v , 1 2 CRLB \approx \frac{6\sigma^2}{\pi^2E{A_{v,1}}^2} CRLB≈π2EAv,126σ2
-
3 分析了FMCW线性调频脉冲非线性的影响
- 周期性偏差不会影响检测精度,因为BMAC算法具有非线性缓解作用
- 随机频率偏差会影响身体运动抑制的性能, 如下图
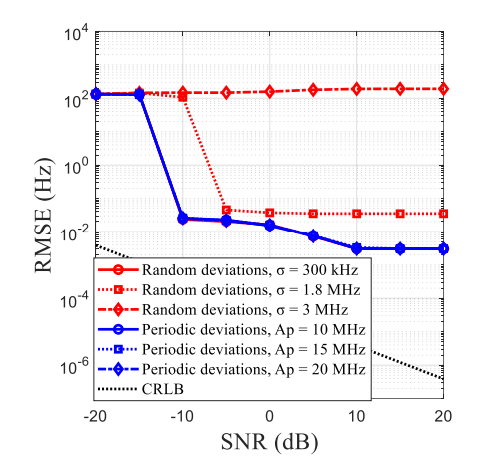
- 当 σ f \sigma_f σf=3 MHz时,很难估计振动,因为所提出的BMAC算法未能准确提取身体运动
4 Experiment Result
-
使用60 GHz FMCW雷达进行了咳嗽检测实验
-
人体目标位于0.8米处
-
受测时自愿咳嗽
-
雷达参数:
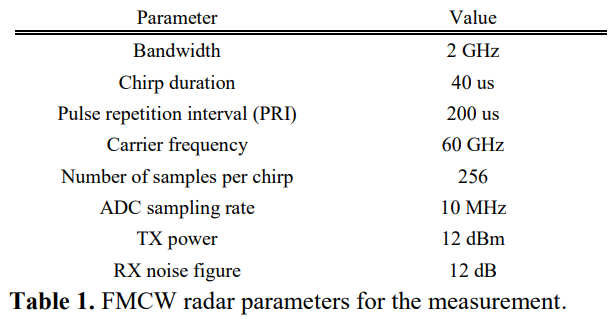
-
-
为了比较检测到的咳嗽频率峰值,对处理后的信号执行短时傅里叶变换(STFT)
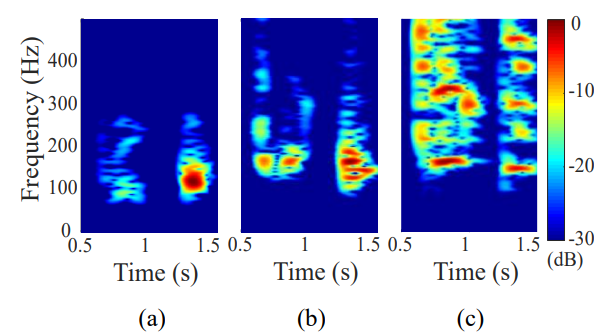
-
由于CPI内咳嗽的基本频率不是常数 ⇒ \Rightarrow ⇒ 用RMSE和RMSPE评估精度
-
测量结果:
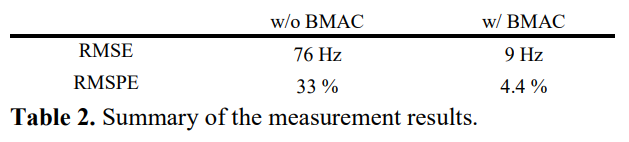
-
使用所提出的雷达系统检测咳嗽信号的RMSE降低到9Hz,相对应频率误差4.4%
-
不使用BMAC算法时检测咳嗽频率的RMSE为76Hz,对应误差33%
-
-
实验结论:方法有效
5 Conclusion
- This paper:
- a signal model
- a processing procedure
- numerical simulations
- experimental validation




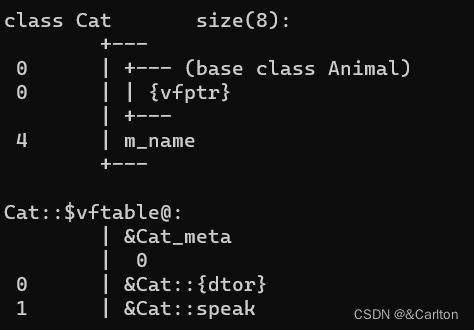



![#P1000. [NOIP2008普及组] 立体图](https://img-blog.csdnimg.cn/img_convert/ec417b4616d72e04a3d2094dd0de1cda.png)

![C++复刻:[流光按钮]+[悬浮波纹按钮]](https://img-blog.csdnimg.cn/cff138cb7b884dd3bc510dbeaea2559e.gif)