介绍
下面以物种多样性为例子展示了如何在R语言中进行相关分析和线性回归分析。
怎么做测试
相关和线性回归示例
Data = read.table(textConnection(Input),header=TRUE)数据简单图
plot(Species ~ Latitude,
data=Data,
pch=16,
xlab = "Latitude",
ylab = "Species") 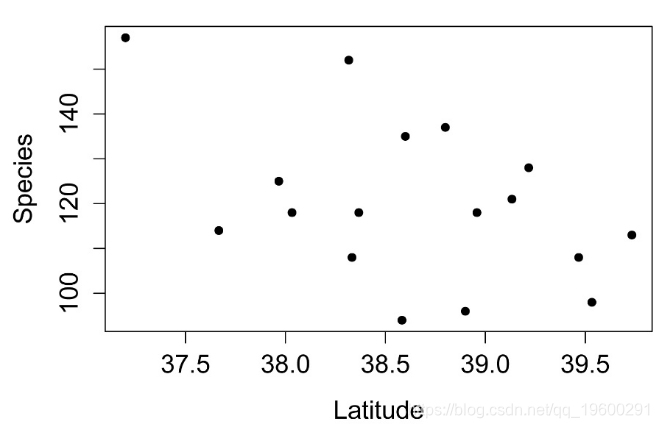
相关性
可以使用 cor.test函数。它可以执行Pearson,Kendall和Spearman相关。
皮尔逊相关
皮尔逊相关是最常见的相关形式。假设数据是线性相关的,并且残差呈正态分布。
cor.test( ~ Species + Latitude,
data=Data,
method = "pearson",
conf.level = 0.95)
Pearson's product-moment correlation
t = -2.0225, df = 15, p-value = 0.06134
cor
-0.4628844肯德尔相关
肯德尔秩相关是一种非参数检验,它不假设数据的分布或数据是线性相关的。它对数据进行排名以确定相关程度。
cor.test( ~ Species + Latitude,
data=Data,
method = "kendall",
continuity = FALSE,
conf.level = 0.95)
Kendall's rank correlation tau
z = -1.3234, p-value = 0.1857
tau
-0.2388326斯皮尔曼相关
Spearman等级相关性是一种非参数检验,它不假设数据的分布或数据是线性相关的。它对数据进行排序以确定相关程度,并且适合于顺序测量。
线性回归
线性回归可以使用 lm函数执行。可以使用lmrob函数执行稳健回归。
summary(model) # shows parameter estimates,
# p-value for model, r-square
Estimate Std. Error t value Pr(>|t|)
(Intercept) 585.145 230.024 2.544 0.0225 *
Latitude -12.039 5.953 -2.022 0.0613 .
Multiple R-squared: 0.2143, Adjusted R-squared: 0.1619
F-statistic: 4.09 on 1 and 15 DF, p-value: 0.06134
Response: Species
Sum Sq Df F value Pr(>F)
Latitude 1096.6 1 4.0903 0.06134 .
Residuals 4021.4 15绘制线性回归
plot(Species ~ Latitude,
data = Data,
pch=16,
xlab = "Latitude",
ylab = "Species")
abline(int, slope,
lty=1, lwd=2, col="blue") # style and color of line 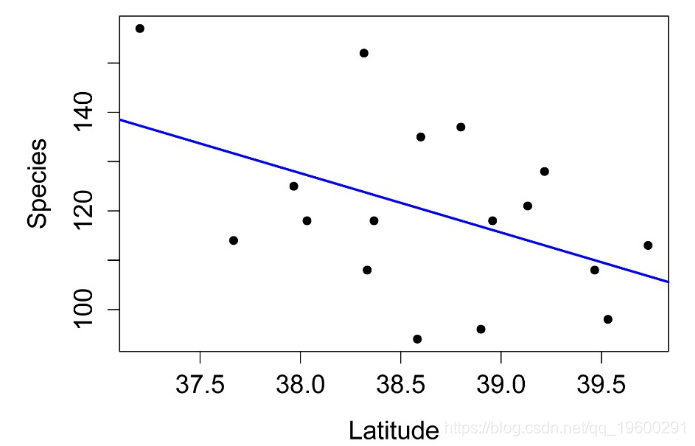
检查模型的假设
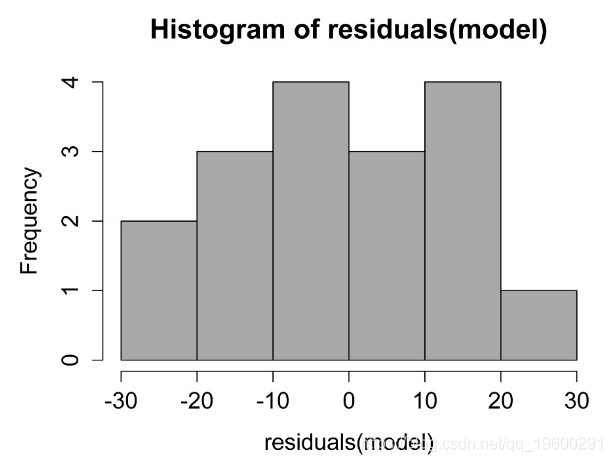
线性模型中残差的直方图。这些残差的分布应近似正态。
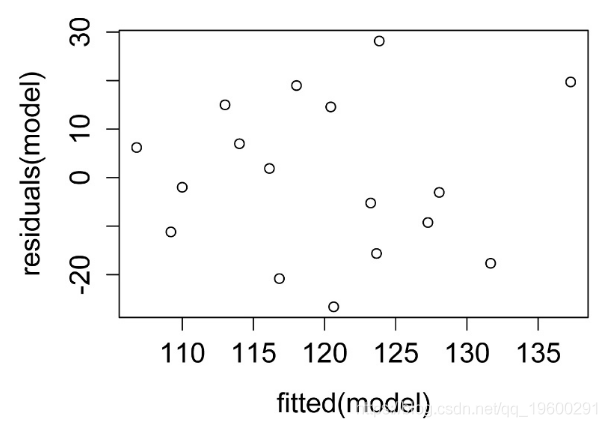
残差与预测值的关系图。残差应无偏且均等。
稳健回归
该线性回归对响应变量中的异常值不敏感。
summary(model) # shows parameter estimates, r-square
Estimate Std. Error t value Pr(>|t|)
(Intercept) 568.830 230.203 2.471 0.0259 *
Latitude -11.619 5.912 -1.966 0.0681 .
Multiple R-squared: 0.1846, Adjusted R-squared: 0.1302
anova(model, model.null) # shows p-value for model
pseudoDf Test.Stat Df Pr(>chisq)
1 15
2 16 3.8634 1 0.04935 *绘制模型
线性回归示例
summary(model) # shows parameter estimates,
# p-value for model, r-square
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.6890 4.2009 3.021 0.0056 **
Weight 1.6017 0.6176 2.593 0.0154 *
Multiple R-squared: 0.2055, Adjusted R-squared: 0.175
F-statistic: 6.726 on 1 and 26 DF, p-value: 0.0154
### Neither the r-squared nor the p-value agrees with what is reported
### in the Handbook.
library(car)
Anova(model, type="II") # shows p-value for effects in model
Sum Sq Df F value Pr(>F)
Weight 93.89 1 6.7258 0.0154 *
Residuals 362.96 26
# # #功率分析
功率分析的相关性
### --------------------------------------------------------------
### Power analysis, correlation
### --------------------------------------------------------------
pwr.r.test()
approximate correlation power calculation (arctangh transformation)
n = 28.87376