文章目录
- 前言
- 一、调制简介
- 1、调制定义
- 2、调制目的
- 3、调制的分类
- 二、幅度调制(线性调制)
- 1、幅度调制的一般模型
- 2、常规双边带调幅 AM
- ①、AM 信号的产生
- ②、AM 调制器的模型
- ③、AM 波形和频谱
- ④、AM 信号的特点
- ⑤、AM 包络检波
- ⑥、调幅系数
- 3、抑制载波双边带 DSB
- ①、如何提高调制效率?
- ②、DSB 波形与频谱
- ③、DSB 信号的特点
- ④、相干解调(同步检波)
- 4、单边带调制 SSB
- ①、SSB 信号的产生
- (1)滤波法
- (2)相移法
- ②、SSB 信号的特点
- 5、残留边带调制 VSB
- ①、VSB 滤波器特性 H ( ω ) H(\omega) H(ω) 应满足什么条件
- ②、VSB 滤波器的几何解释
- ③、VSB 信号的特点
- 6、AM/DSB/SSB/VSB 关系
- 三、角度调制(非线性调制)
- 1、调频和调相的基本概念
- 2、两者关系
- 3、FM 和带宽
- ①、调频参数和最大频偏
- ②、FM 频谱
- ③、FM 带宽
- 4、FM 信号的产生与解调
- ①、FM 信号的产生
- ②、FM 信号的解调(鉴频)
- 5、FM 特点与应用
- ①、FM 特点
- ②、FM 应用
前言
记录通信原理中调制和解调相关学习笔记。
一、调制简介
1、调制定义
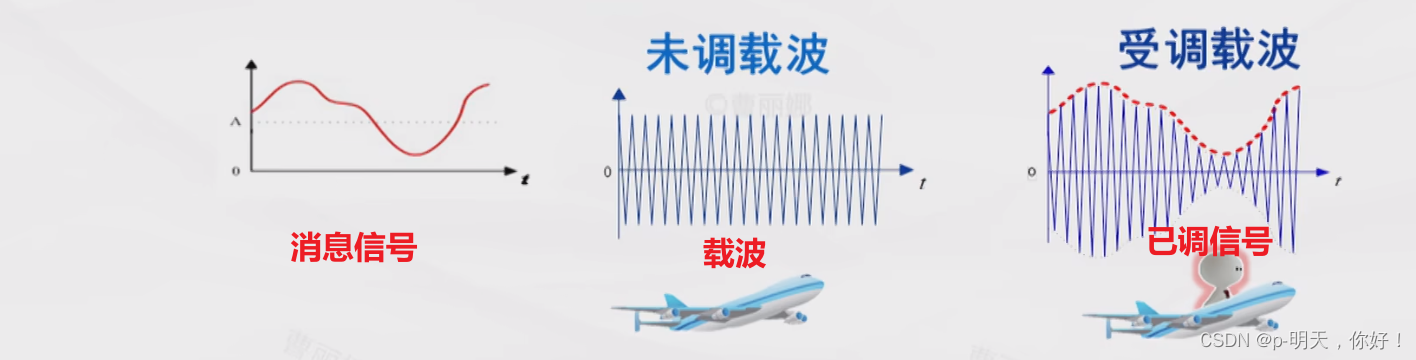
比喻——货物运输:将货物装载到飞机/轮船的某个仓位上
调制:把消息信号搭载到载波的某个参数上,形成已调信号。
载波:某种高频周期性振荡信号,如正弦波。
受调载波称为已调信号,含有消息信号特征。
解调:调制的逆过程,从已调信号中恢复信息信号。
2、调制目的
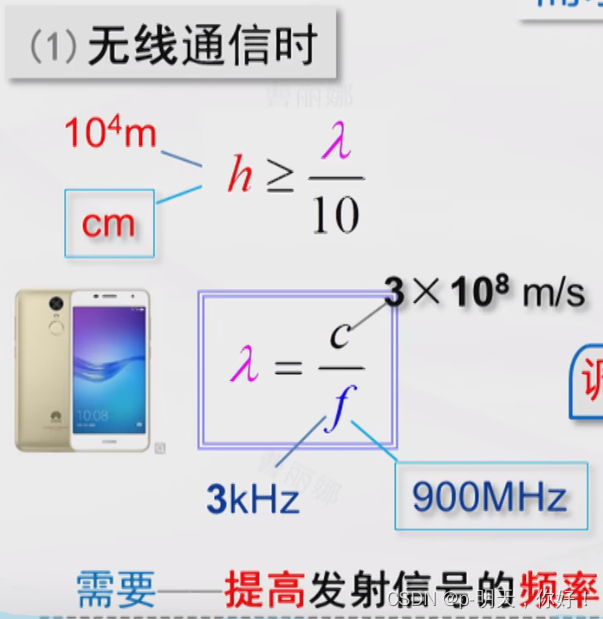
- 匹配信道特性,减小天线尺寸,提高辐射效率
- 频谱搬移,实现信道的多路复用,提高信道利用率
- 扩展信号带宽,提高系统抗干扰能力
- 实现带宽与信噪比的互换(有效性和可靠性)
通过提高发射信号的频率进而减小制作天线的尺寸长度。
3、调制的分类
①、调制的过程
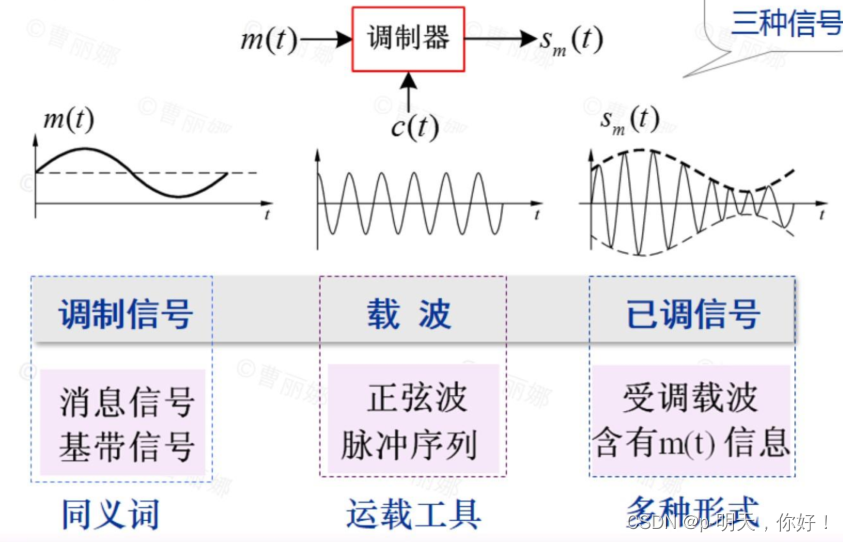
②、下图展示了都有哪些调制方式:
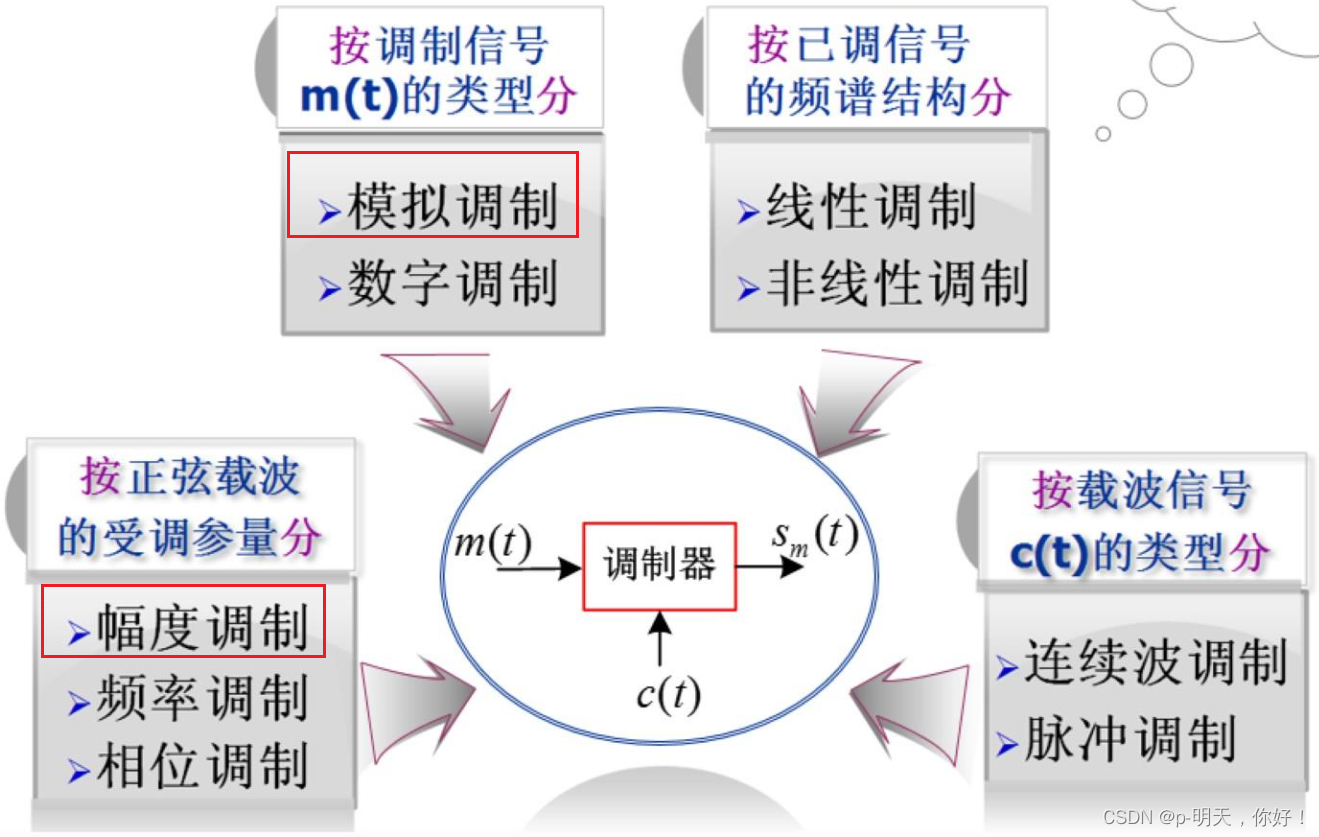
二、幅度调制(线性调制)
1、幅度调制的一般模型
幅度调制——消息信号控制正弦载波的幅度
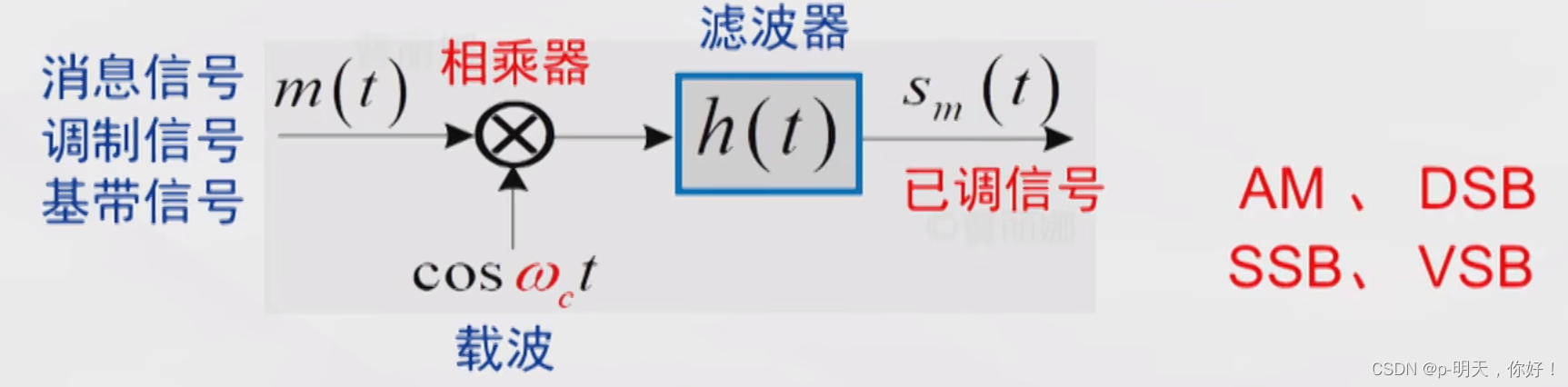
时域:
S
m
(
t
)
=
[
m
(
t
)
cos
ω
c
t
]
∗
h
(
t
)
S_m(t)=[m(t)\cos\omega_ct]*h(t)
Sm(t)=[m(t)cosωct]∗h(t)
频域:
S
m
(
t
)
=
1
2
[
M
(
ω
+
ω
c
)
+
M
(
ω
−
ω
c
)
]
H
(
ω
)
S_m(t)=\frac{1}{2}[M(\omega+\omega_c)+M(\omega-\omega_c)]H(\omega)
Sm(t)=21[M(ω+ωc)+M(ω−ωc)]H(ω)
m
(
t
)
↔
M
(
ω
)
m(t) \leftrightarrow M(\omega)
m(t)↔M(ω);
h
(
t
)
↔
H
(
ω
)
h(t) \leftrightarrow H(\omega)
h(t)↔H(ω)
2、常规双边带调幅 AM
①、AM 信号的产生
条件:设消息信号
m
(
t
)
m(t)
m(t) 的均值为 0,即
m
(
t
)
‾
=
0
\overline{m(t)}=0
m(t)=0,且
∣
m
(
t
)
∣
m
a
x
≤
A
0
\mid m(t) \mid_{max}\leq A_0
∣m(t)∣max≤A0,外加直流偏执
A
0
A_0
A0,然后与载波进行相乘,即可得到 AM 信号。
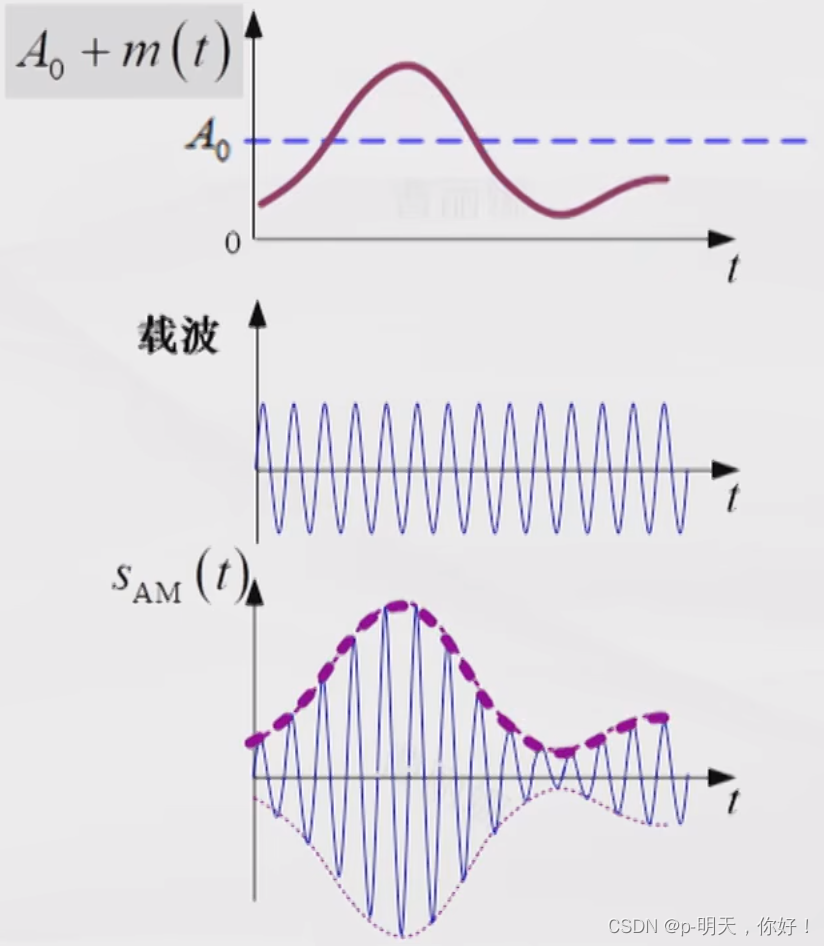
②、AM 调制器的模型
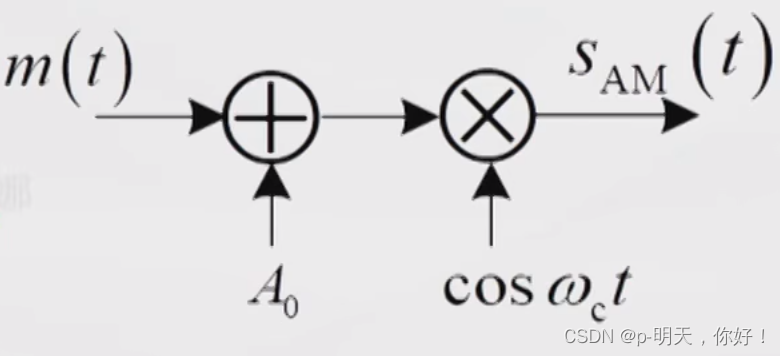
③、AM 波形和频谱
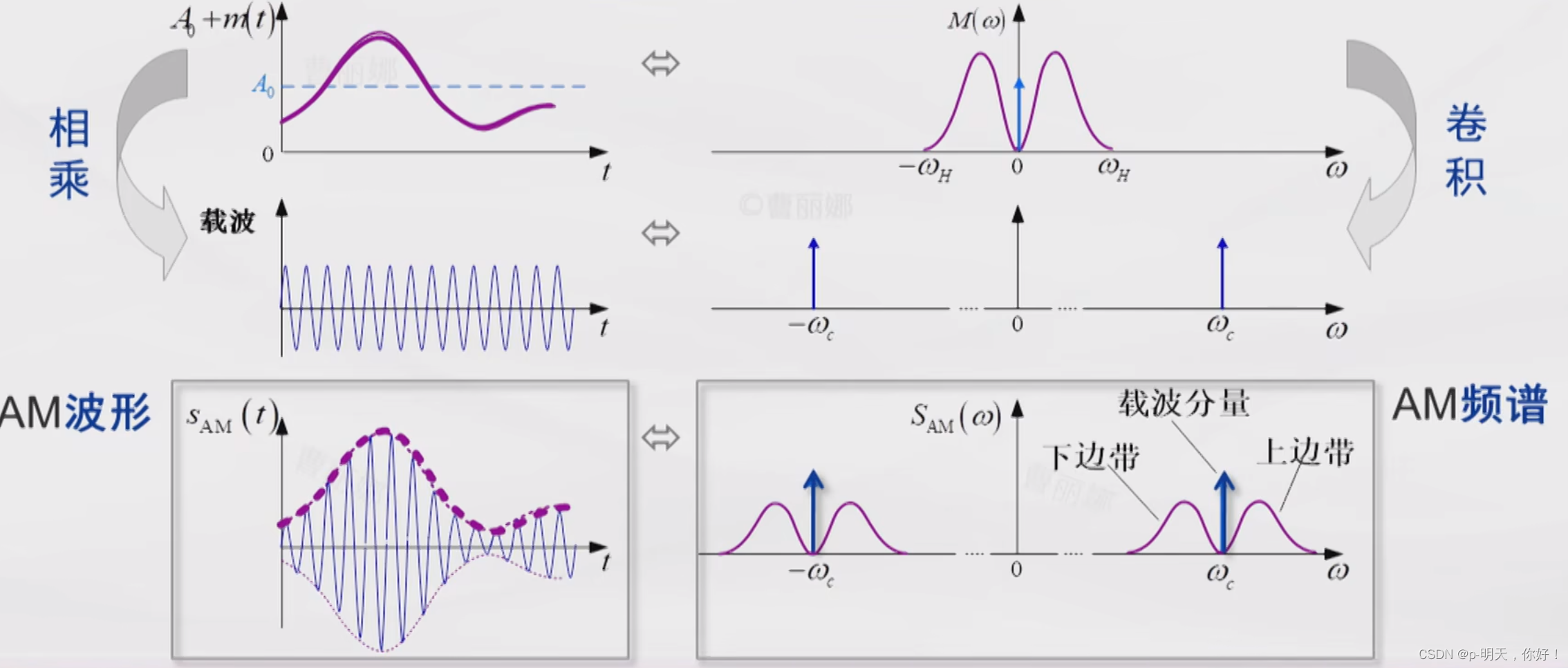
④、AM 信号的特点
- ∣ m ( t ) ∣ m a x ≤ A 0 \mid m(t) \mid_{max}\leq A_0 ∣m(t)∣max≤A0 时,AM 波的包络正比于调频信号 m ( t ) m(t) m(t),故可采用包络检波。
- AM 的频谱由载频分量、上边带和下边带组成。
- AM 传输带宽是调制信号带宽的两倍, B A M = 2 f H B_{AM}=2f_H BAM=2fH。
- AM 的优势在于接收机简单,广泛用于中短调幅广播。
- AM 的缺点主要是调制效率(功率利用率)低。( η A M ≤ 50 \eta_{AM}\leq50% ηAM≤50%)
⑤、AM 包络检波
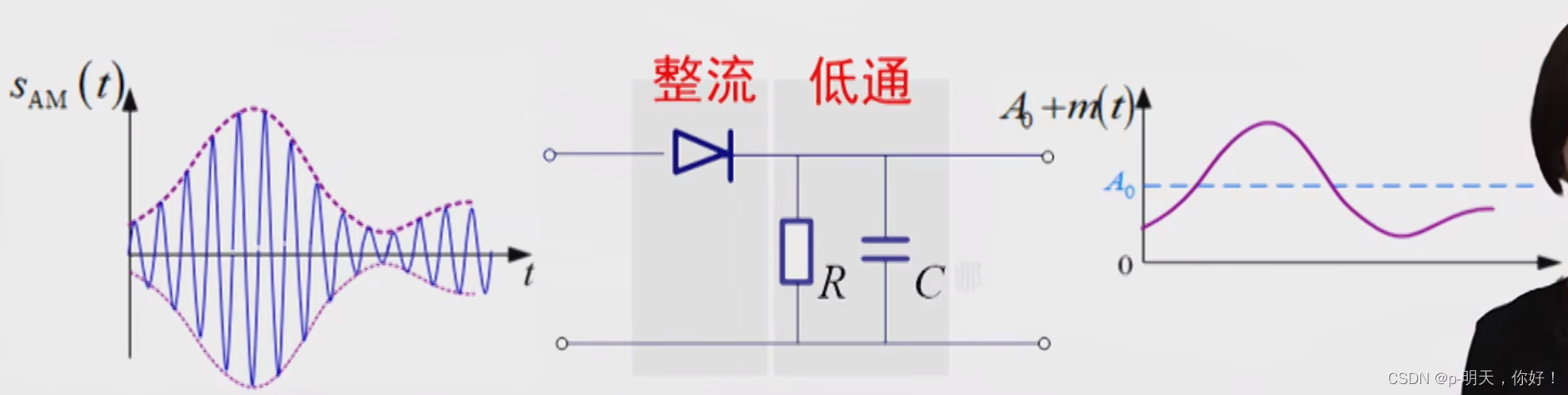
条件:
∣
m
(
t
)
∣
m
a
x
≤
A
0
\mid m(t) \mid_{max}\leq A_0
∣m(t)∣max≤A0
特点:简单;不需要相干载波(非相干解调);但是,小信噪比时有门限效应。
⑥、调幅系数
——反映调幅信号
m
(
t
)
m(t)
m(t) 改变载波幅度的程度
——涉及 AM 的功率分配和调制效率
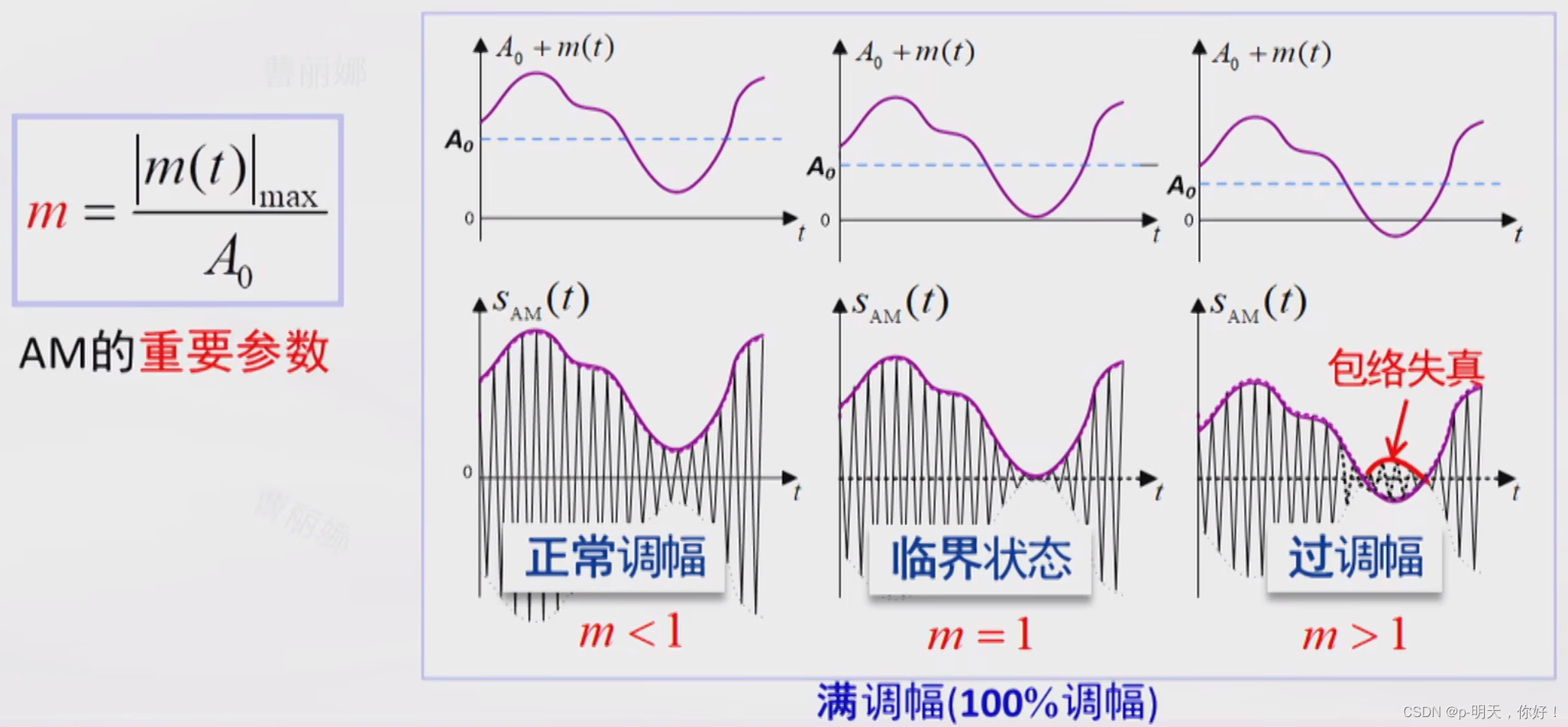
3、抑制载波双边带 DSB
①、如何提高调制效率?
—— 抑制已调信号中的载波分量(等效于去掉基带信号中的直流偏执 A 0 A_0 A0),这种方式称为抑制载波的双边带调制,简称双边带调制 DSB
②、DSB 波形与频谱
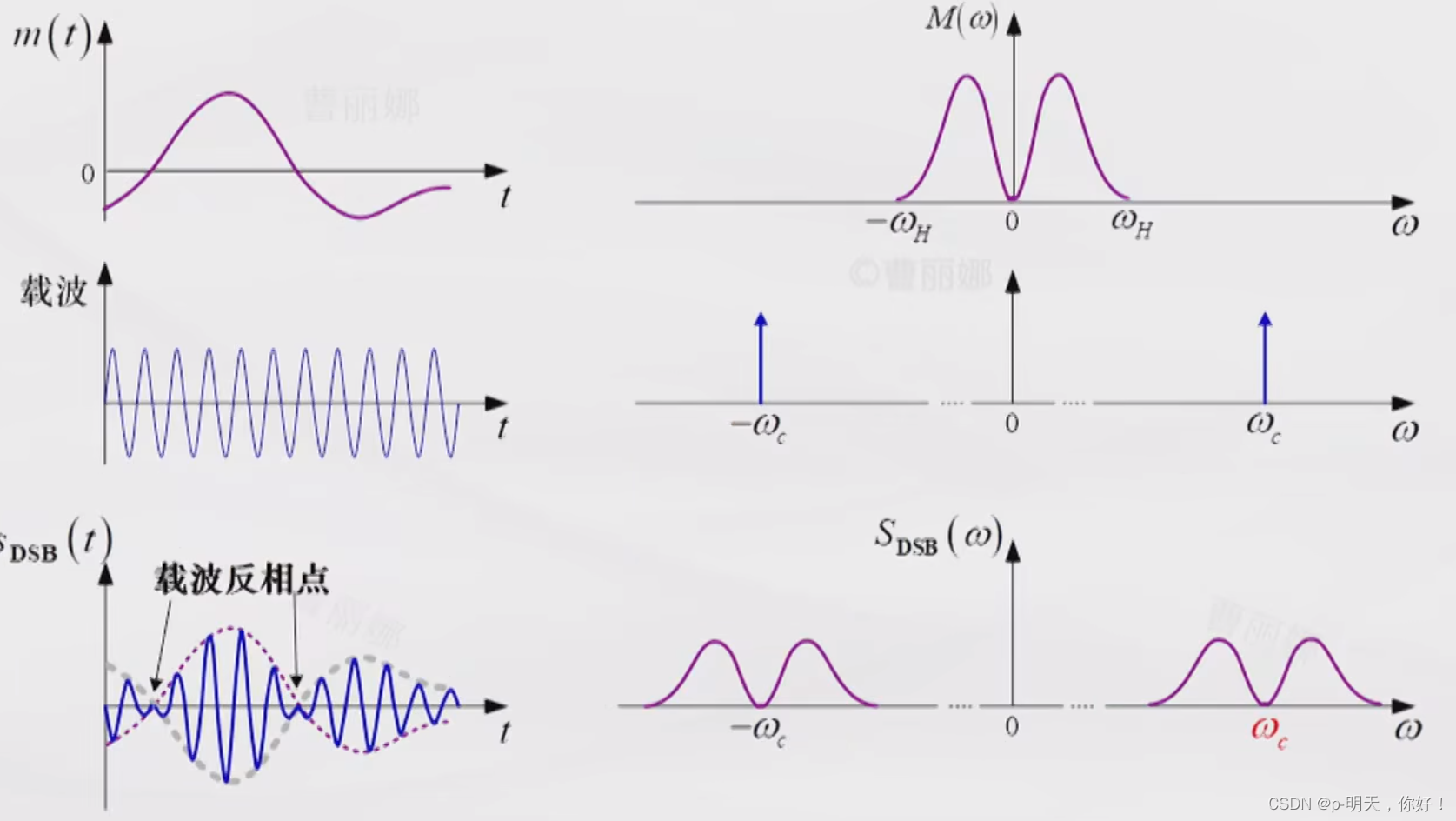
③、DSB 信号的特点
- 包络不再与 m ( t ) m(t) m(t) 成正比;当 m ( t ) m(t) m(t) 改变符号时载波相位反转,故不能用包络检波,需要相干解调。
- 五载频分量,只有上、下边带。
- 带宽与 AM 的相同: B D S B = B A M = 2 f H B_{DSB}=B_{AM}=2f_H BDSB=BAM=2fH。
- 调制效率 100%,即功率利用率高。
- 主要用作 SSB、VSB 的技术基础,调频立体声中的差信号调制等。
④、相干解调(同步检波)
采用相干解调的方式解调 DSB 信号
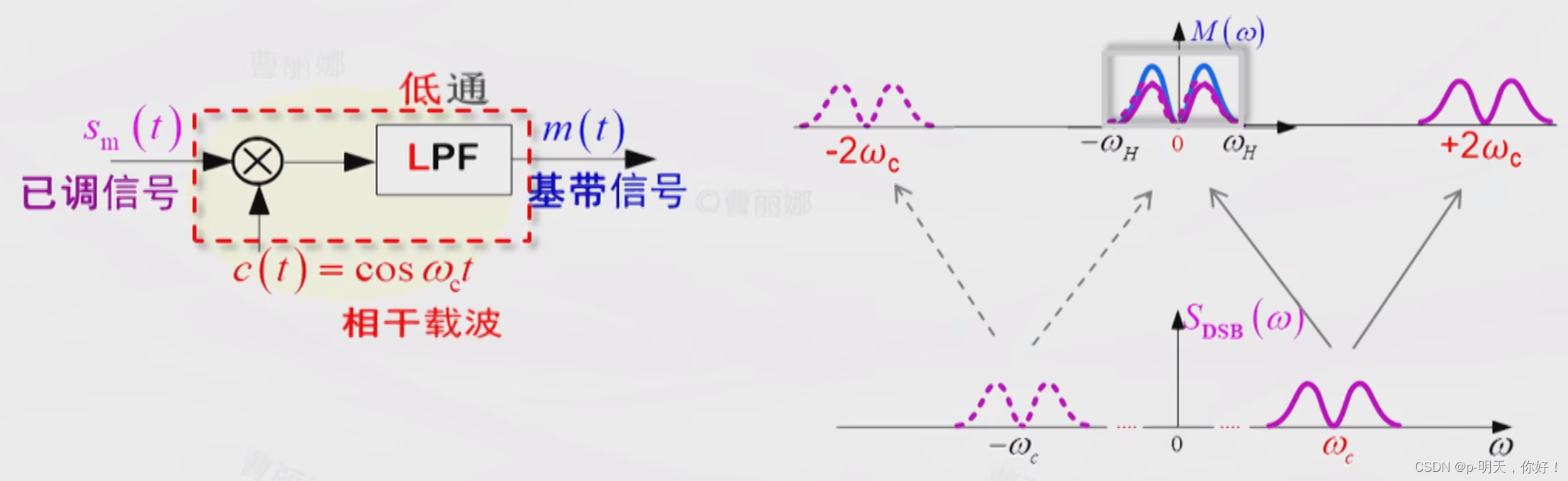
适用:AM、DSB、SSB、VSB
要求:载波同步
c
(
t
)
=
cos
ω
c
t
c(t)=\cos\omega_ct
c(t)=cosωct ——本地载波(相干载波-----与调制载波同频同向)
若接收端提供的本地载波不相干(如同频不同向),那么对解调带来衰减甚至失真问题
4、单边带调制 SSB
①、SSB 信号的产生
(1)滤波法
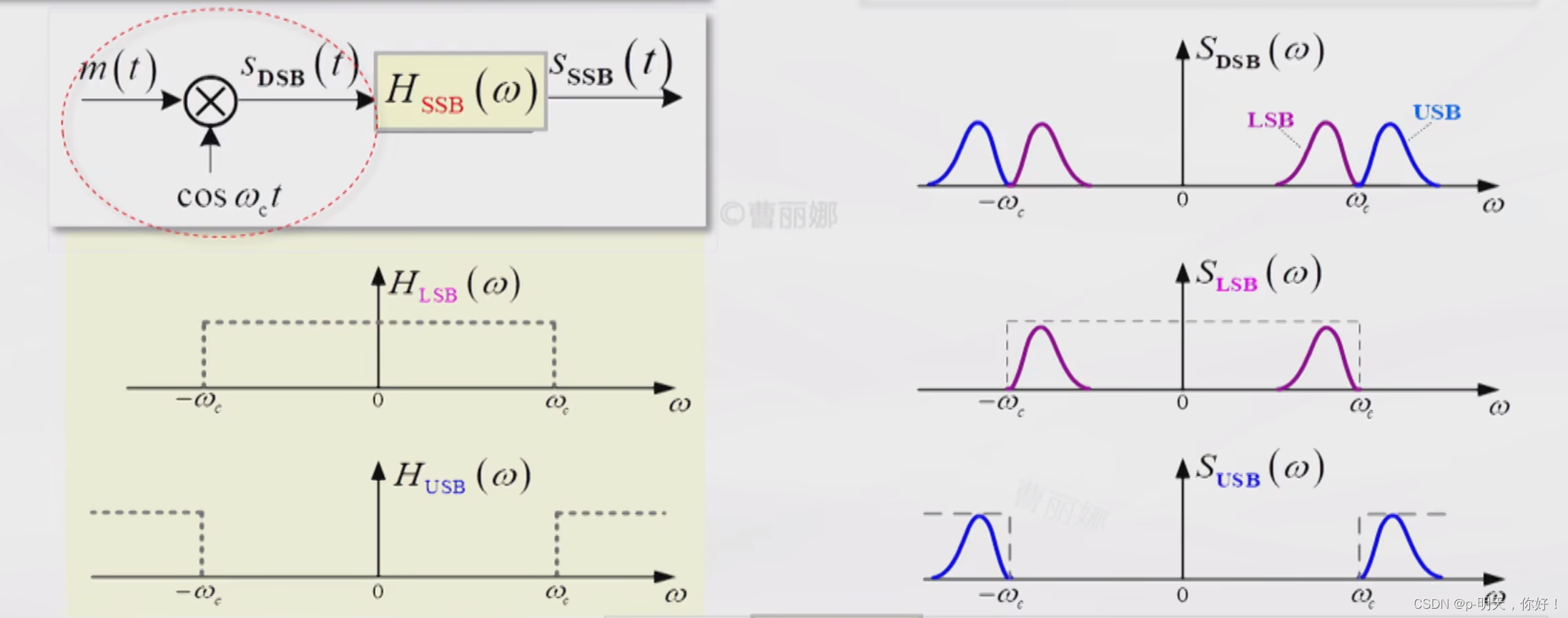
原理:先形成 DSB 信号,边带滤波即得上或下边带信号
要求:滤波器
H
S
S
B
(
ω
)
H_{SSB}(\omega)
HSSB(ω) 在载频处具有陡峭的截止特性。—— 技术难点之一
(2)相移法
S
S
S
B
(
t
)
=
1
2
m
(
t
)
cos
ω
c
t
±
1
2
m
(
t
)
^
sin
ω
c
t
——
S
S
B
表达式
S_{SSB}(t)=\frac{1}{2}m(t)\cos\omega_ct\pm\frac{1}{2}\hat{m(t)}\sin\omega_ct——SSB表达式
SSSB(t)=21m(t)cosωct±21m(t)^sinωct——SSB表达式
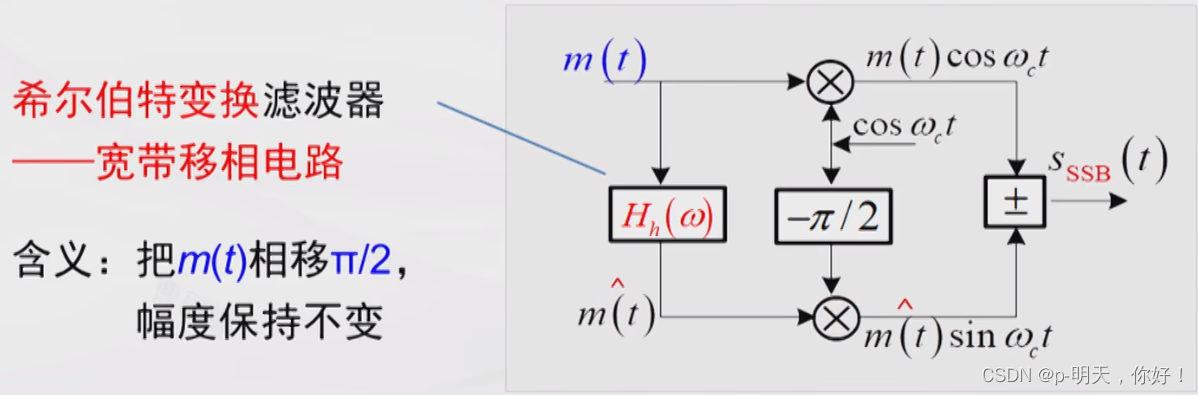
②、SSB 信号的特点
- 优点之一是频带利用率高。其传输带宽仅为 AM/DSB 的一半: B S S B = B A M / 2 = f H B_{SSB}=B_{AM}/2=f_H BSSB=BAM/2=fH,因此,在频谱拥挤的通信场合获得了广泛应用,尤其在短波通信和多路载波电话中占有重要的地位。
- 优点之二是低功耗特性,因为不需传送载波和另一个边带而节省了功率。这一点对于移动通信系统尤为重要。
- 缺点是设备较复杂,存在技术难点。也需相干解调。
5、残留边带调制 VSB
—— 介于 SSB 和 DSB 之间的折中方案
**单边带存在的问题是难以实现陡峭的边带滤波特性。解决办法是逐步切割,圆滑滚将。
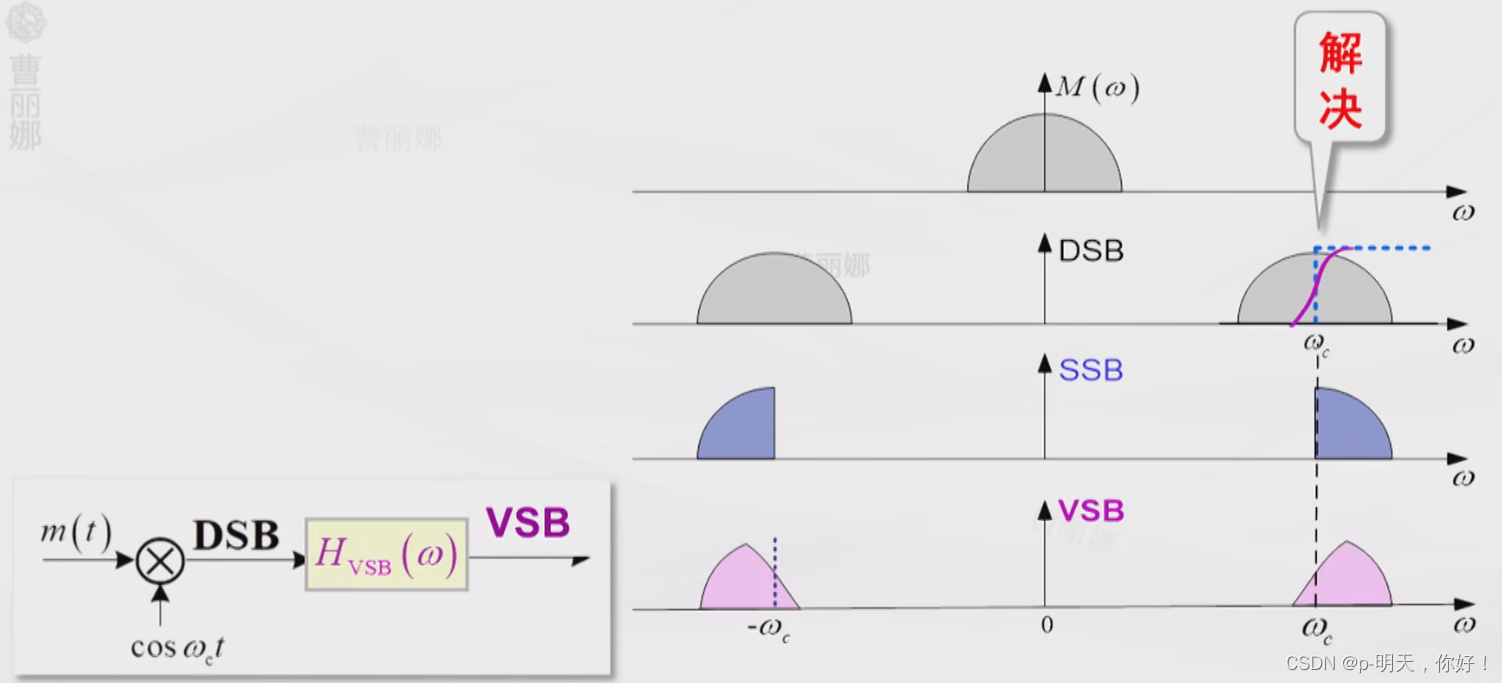
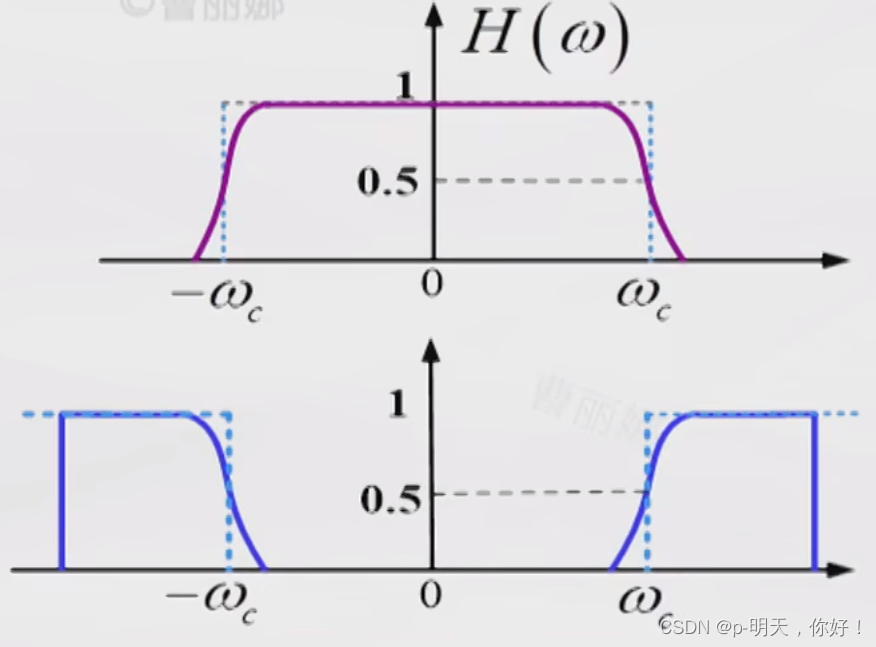
①、VSB 滤波器特性 H ( ω ) H(\omega) H(ω) 应满足什么条件
若要无失真恢复
m
(
t
)
m(t)
m(t),
H
(
ω
)
H(\omega)
H(ω) 应满足如下条件:
[
H
(
ω
+
ω
c
)
+
H
(
ω
−
ω
c
)
]
=
常数,
∣
ω
∣
≤
ω
H
[H(\omega+\omega_c)+H(\omega-\omega_c)]=常数,|\omega|\leq\omega_H
[H(ω+ωc)+H(ω−ωc)]=常数,∣ω∣≤ωH
含义:
H
(
ω
)
H(\omega)
H(ω) 必须满足:在载频处具有互补对称特性
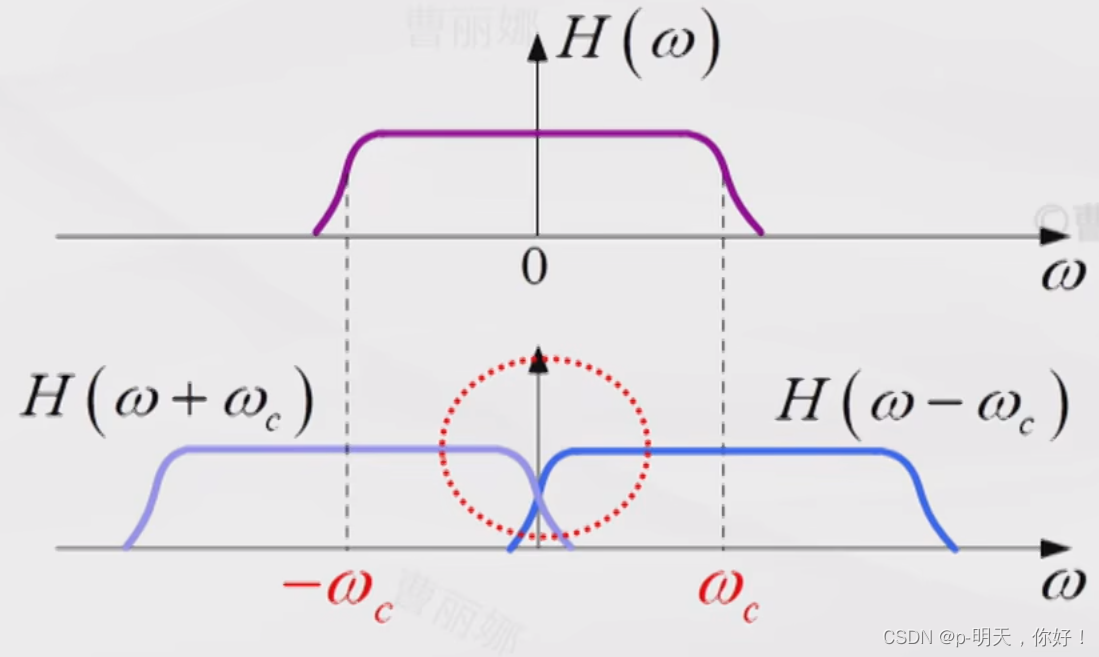
②、VSB 滤波器的几何解释
是将具有互补对称的特性左右平移
ω
c
\omega_c
ωc 叠加的结果,等于常数
[
H
(
ω
+
ω
c
)
+
H
(
ω
−
ω
c
)
]
=
常数,
∣
ω
∣
≤
ω
H
[H(\omega+\omega_c)+H(\omega-\omega_c)]=常数,|\omega|\leq\omega_H
[H(ω+ωc)+H(ω−ωc)]=常数,∣ω∣≤ωH
③、VSB 信号的特点
- 仅比 SSB 所需带宽有很小的增加,却换来了电路的简单。 f H < B V S B < 2 f H f_H<B_{VSB}<2f_H fH<BVSB<2fH。
- 应用:商业电视广播中的视频信号传输等。
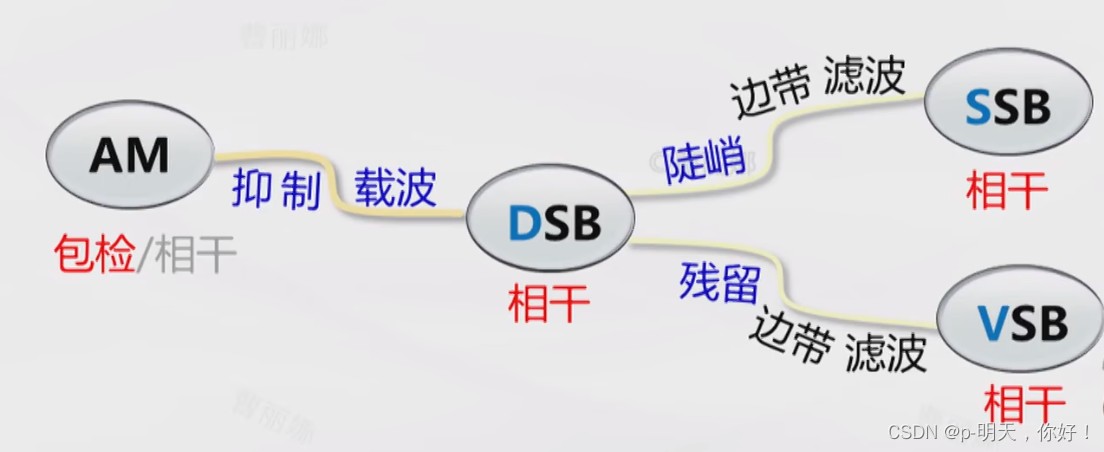
6、AM/DSB/SSB/VSB 关系
三、角度调制(非线性调制)
由于频率和相位是微积分的关系,所以无论调频还是调相,都会使载波的角度发生变化,所以调频和调相统称为角度调制。
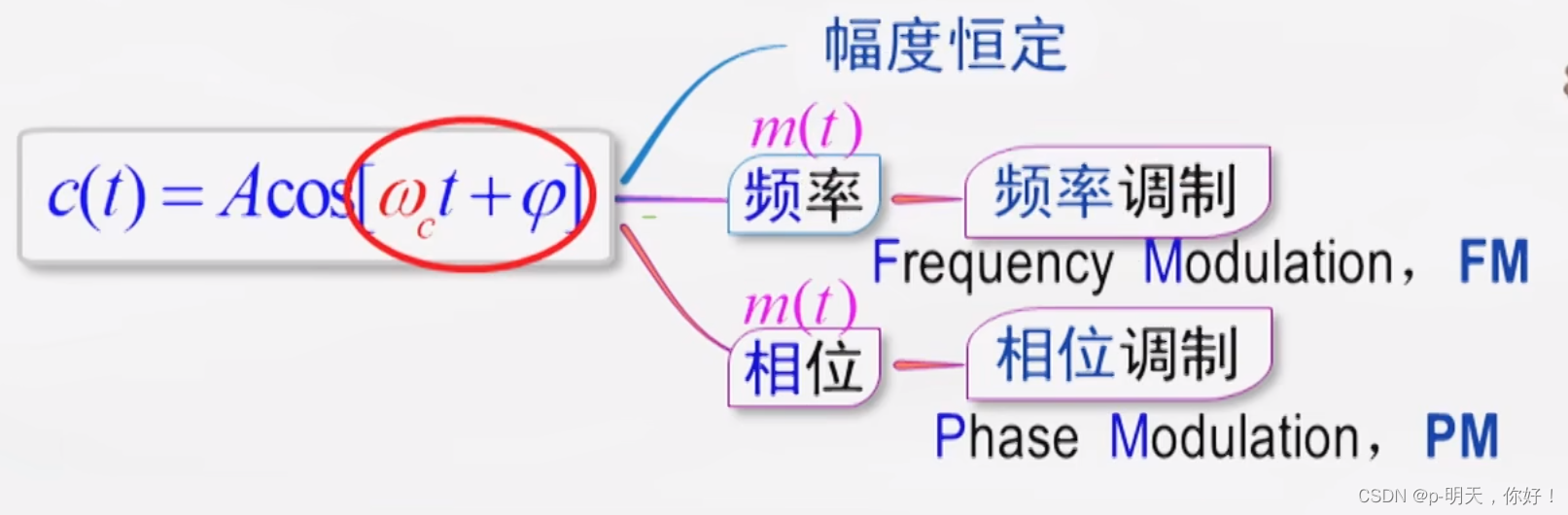
1、调频和调相的基本概念
角调信号: S m ( t ) = A cos [ ω c t + ϕ ( t ) ] S_m(t)=A\cos[\omega_ct+\phi(t)] Sm(t)=Acos[ωct+ϕ(t)],其中幅度 A A A 恒定, ϕ ( t ) \phi(t) ϕ(t) 随 m ( t ) m(t) m(t) 变化
<1>、调相(PM):相位偏移
若相位偏移
ϕ
(
t
)
\phi(t)
ϕ(t) 正比于消息信号
m
(
t
)
m(t)
m(t) 的变化规律,则已调信号为调相信号,其中
K
p
K_p
Kp 是相移常数(rad/V)。
ϕ ( t ) = K p m ( t ) \phi(t)=K_pm(t) ϕ(t)=Kpm(t)
S P M = A cos [ ω c ( t ) + K p m ( t ) ] S_{PM}=A\cos[\omega_c(t)+K_pm(t)] SPM=Acos[ωc(t)+Kpm(t)]
<2>、调频(FM):角频偏
若角频偏
d
ϕ
(
t
)
d
t
\frac{d\phi(t)}{dt}
dtdϕ(t) 正比于消息信号
m
(
t
)
m(t)
m(t),而相位偏移
ϕ
(
t
)
\phi(t)
ϕ(t) 正比于消息信号
m
(
t
)
m(t)
m(t) 的积分,则已调信号为调频信号,其中
K
f
K_f
Kf 为频偏常数(Hz/V),表示单位调制电压产生的频偏量,也称调频灵敏度。
d ϕ ( t ) d t = 2 π K f m ( t ) \frac{d\phi(t)}{dt}=2\pi K_fm(t) dtdϕ(t)=2πKfm(t)
ϕ ( t ) = 2 π K f ∫ m ( τ ) d τ \phi(t)=2\pi K_f\int m(\tau)d\tau ϕ(t)=2πKf∫m(τ)dτ
S F M = A cos [ ω c ( t ) + 2 π K f ∫ m ( τ ) d τ ] S_{FM}=A\cos[\omega_c(t)+2\pi K_f\int m(\tau)d\tau] SFM=Acos[ωc(t)+2πKf∫m(τ)dτ]
2、两者关系
由于频率和相位是微分积分关系:
频率 ~ 相位:微分积分
调相 ~ 调频:相互转化
①、若把调制信号
m
(
t
)
m(t)
m(t) 先微分再调频,则可得到调相信号
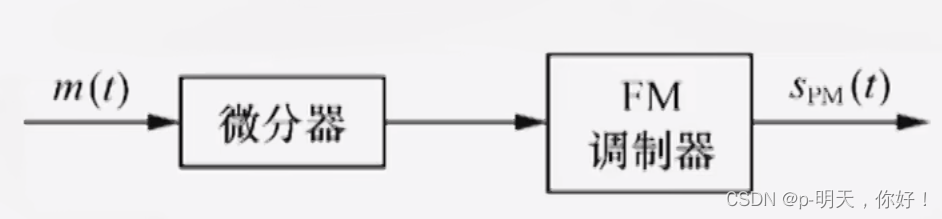
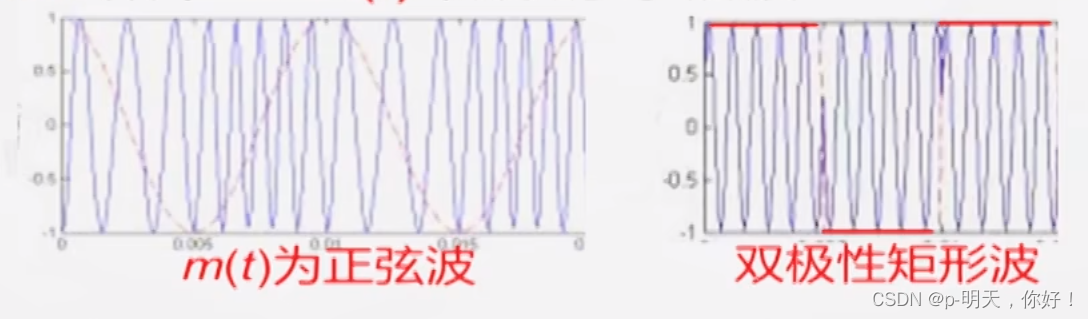
调相波 PM 是频率正比于调制信号
m
(
t
)
m(t)
m(t) 微分的等幅波,下面给出了消息信号是正弦波和矩形脉冲的两种情况
②、若把调制信号
m
(
t
)
m(t)
m(t) 先积分再调相,则可得到调频信号

调频波 FM 是频率正比于调制信号
m
(
t
)
m(t)
m(t) 的等幅波,它的波形的疏密随着消息信号
m
(
t
)
m(t)
m(t) 的大小变化,即
m
(
t
)
m(t)
m(t) 越大 -> 频率越高 -> 波形越密

3、FM 和带宽
①、调频参数和最大频偏
从单音信号入手,单音 m ( t ) = A m ( t ) cos ω m t m(t)=A_m(t)\cos\omega_mt m(t)=Am(t)cosωmt, ω m = 2 π f m \omega_m=2\pi f_m ωm=2πfm
最大频偏: Δ f = K f A m \Delta f=K_fA_m Δf=KfAm
调频指数(最大相位偏移): m f = Δ f f m = K f A m f m m_f=\frac{\Delta f}{f_m}=\frac{K_fA_m}{f_m} mf=fmΔf=fmKfAm,注: f m f_m fm 为调制频率
调频指数是调频波的一个重要参量,涉及到 FM 的传输带宽、功率分配以及抗噪性能
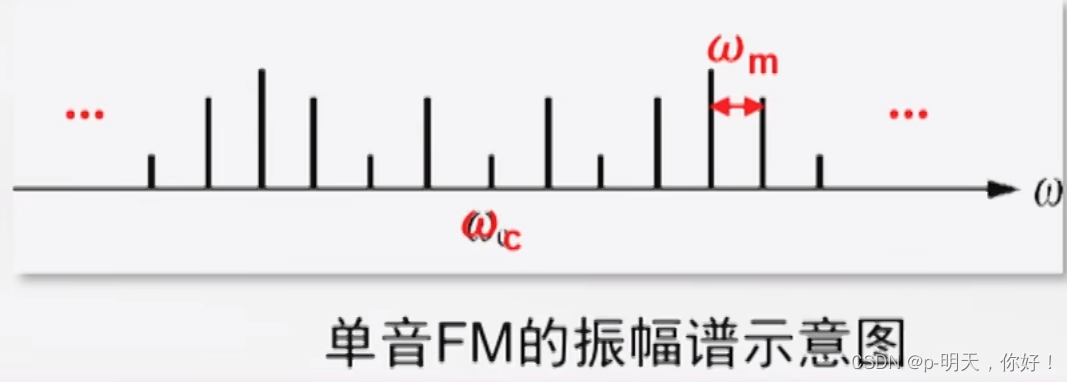
②、FM 频谱
调频信号的频谱是由分布在载频分量
ω
c
\omega_c
ωc 两侧的无数多对边频
ω
c
±
n
ω
m
\omega_c \pm n\omega_m
ωc±nωm 组成,其幅度取决于
m
f
m_f
mf(调频指数)
③、FM 带宽
从理论上讲, FM 信号的带宽为无穷大,但是从工程应用的角度来讲,在下面频带内,集中了98%的信号功率
常用卡森公式计算调频波的带宽:
B
F
M
=
2
(
m
f
+
1
)
f
m
=
2
Δ
f
+
2
f
m
B_{FM}=2(m_f+1)f_m=2\Delta f+2f_m
BFM=2(mf+1)fm=2Δf+2fm
- B F M ≈ 2 f m , m f < < 1 B_{FM}\approx2f_m,m_f<<1 BFM≈2fm,mf<<1 时 —— 窄带调频(NBFM),这个时候带宽取决于调制频率 f m f_m fm
-
B
F
M
≈
2
Δ
f
,
m
f
>
>
1
B_{FM}\approx2\Delta f,m_f>>1
BFM≈2Δf,mf>>1 时 —— 宽带调频(WBFM),这个时候带宽取决于最大频偏
Δ
f
\Delta f
Δf
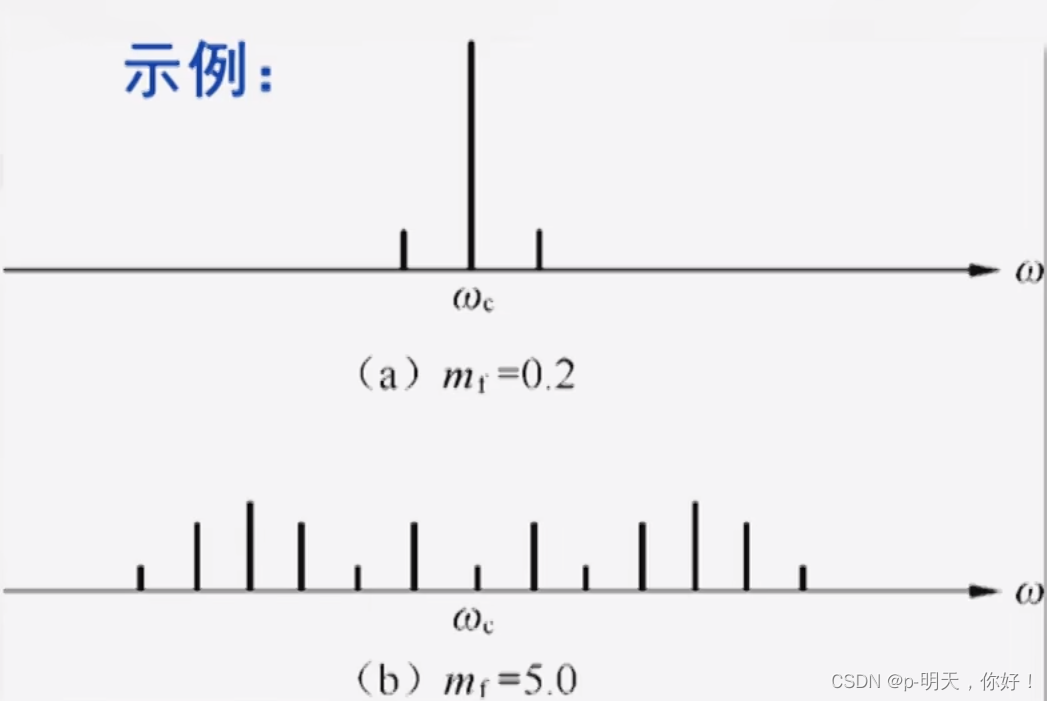
推广:对于多音或任意带限调制信号,FM 带宽:
B F M = 2 ( m f + 1 ) f m B_{FM}=2(m_f+1)f_m BFM=2(mf+1)fm, m f = Δ f f m = K f A m f m m_f=\frac{\Delta f}{f_m}=\frac{K_fA_m}{f_m} mf=fmΔf=fmKfAm, f m f_m fm 为调制信号 m ( t ) m(t) m(t)的最高频率——带宽
4、FM 信号的产生与解调
①、FM 信号的产生
1)直接法
- 原理:调制电压 m ( t ) m(t) m(t) 直接控制振荡器的频率, ω i ( t ) = ω 0 + K f m ( t ) \omega_i(t)=\omega_0+K_fm(t) ωi(t)=ω0+Kfm(t)
- 优点:电路简单,可获得较大频偏
- 缺点:频率稳定度不高
- 改进:采用 PLL 调频器

2)间接法
- 原理:积分 -> 调相 -> n次倍频 ->WBFM
- 优点:频率稳定度好
- 缺点:需要多次倍频和混频,电路较为复杂
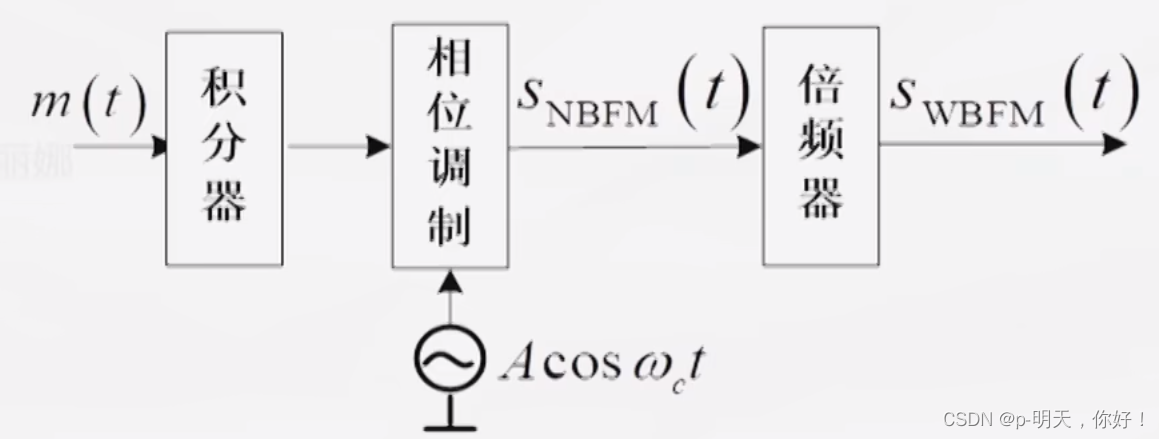
②、FM 信号的解调(鉴频)
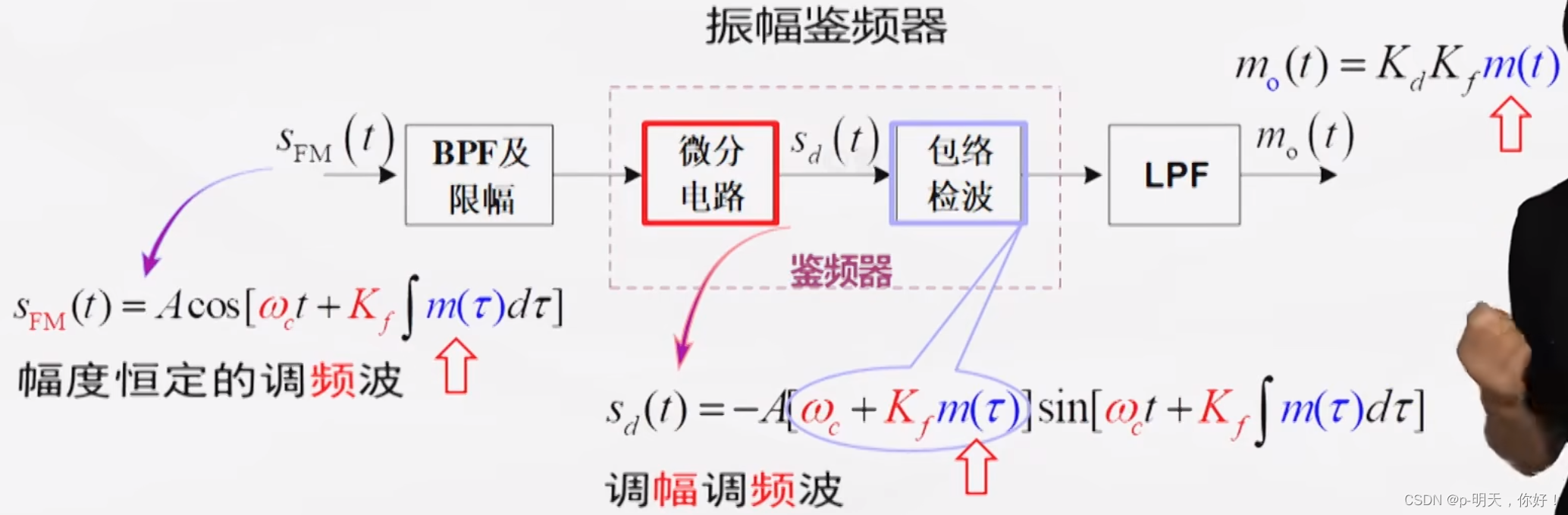
5、FM 特点与应用
①、FM 特点
- 包络恒定(幅度恒定)
- 非线性调制(频偏正比于 m ( t ) m(t) m(t),相偏正比于 m ( t ) m(t) m(t) 的积分)
- 带宽比 AM 大 ( m f + 1 ) (m_f+1) (mf+1) 倍: B F M = 2 ( m f + 1 ) f m B_{FM}=2(m_f+1)f_m BFM=2(mf+1)fm
- 优势:抗噪能力强
- 代价:占用较大信道带宽,频谱利用率低
②、FM 应用
高质量或信道噪声大的场合,如调频广播,电视伴音、卫星通信、移动通信、微波通信和蜂窝电话…。
我的qq:2442391036,欢迎交流!