1005 Out of Control
先将序列a升序,然后离散化
比如说序列a为1000 1000 500 200 10,然后升序后为10 200 500 1000 1000,映射到从1开始的数,为1 2 3 4 4,此即为前缀最大值序列,比如说5 3 4 6 7的前缀最大值序列为5 5 5 6 7
动态规划
f[i][j]表示长度为i的前缀最大值序列中,j为最大元素值的最大方案数
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=3010,mod=1e9+7;
int a[N],b[N];
int f[N][N];
int n;
void solve()
{
cin>>n;
memset(f,0,sizeof f);
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
sort(b+1,b+1+n);
int m=0;
for(int i=1;i<=n;i++){
if(i==1||b[i]>b[i-1]) b[++m]=b[i];//去重
}
sort(a+1,a+1+n);
for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+1+m,a[i])-b;//离散化
for(int i=1;i<=m;i++){
f[1][i]=1;
}
cout<<m<<endl;
for(int i=2;i<=n;i++){
int sum=0,ans=0;
if(a[i-1]<a[i]) (sum+=f[i-1][a[i-1]])%=mod;
for(int j=a[i];j<=m;j++){
(sum+=f[i-1][j])%=mod;
f[i][j]=sum;
(ans+=sum)%=mod;
}
cout<<ans<<endl;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}1011 8-bit Zoom
参考JorbanS
可以先单独考虑z等于100和200的情况
然后判断n*z/100是不是一个整数,可以先令m=n*z/100(下取整),然后再判断m*100是否等于n*z
n*n代表原矩阵的大小,m*m代表放大后的矩阵大小
先求n和m的最大公约数d,表示横着最少分成d块,竖着最少分成d块,也就是说将整个矩阵最少d*d块,每一小块中的字母必须完全相同,否则是放大不了的
nn为每一小块的边长
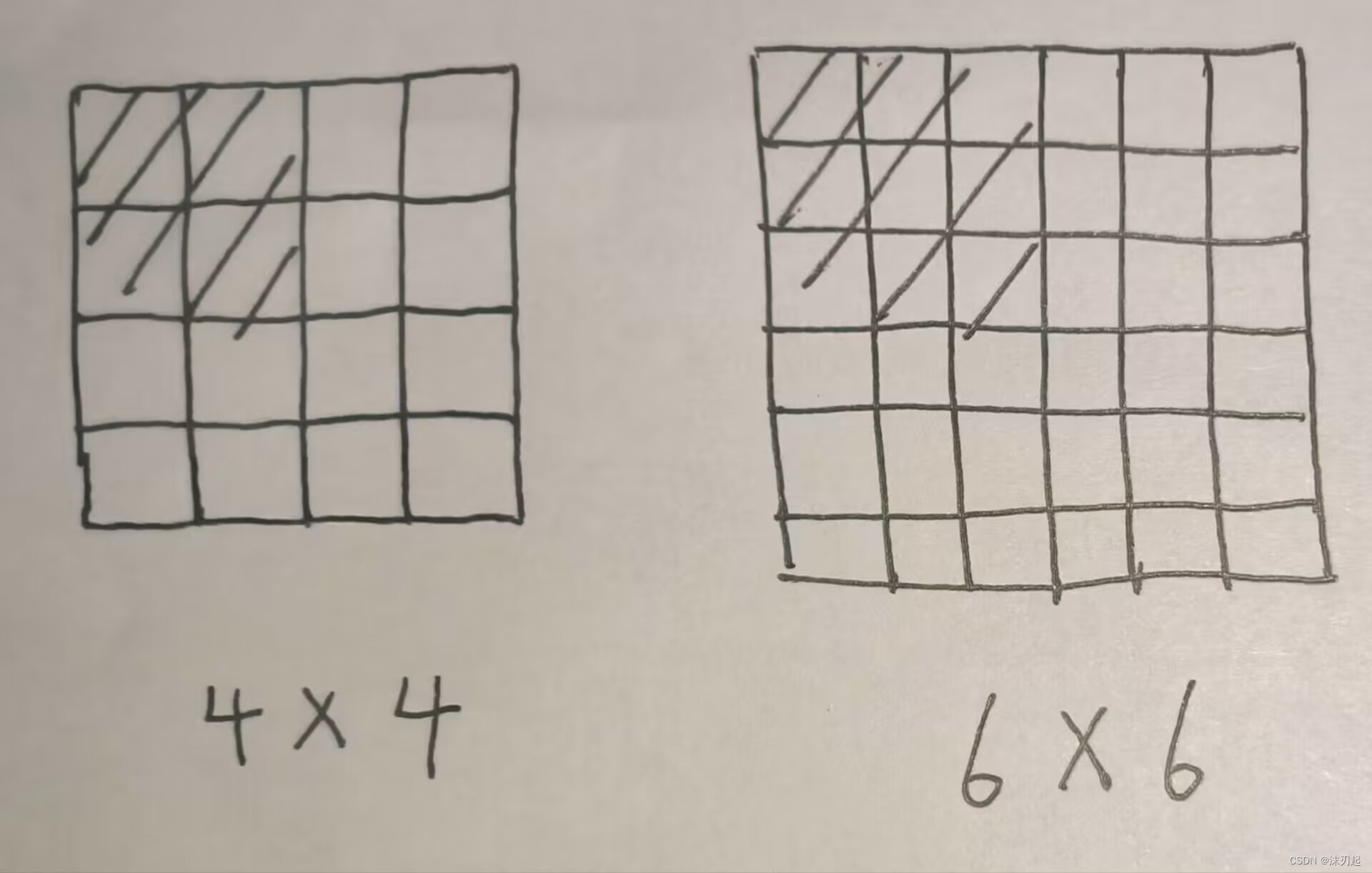
如上图,n为4,m为6,它们的最大公约数为2,所以将其分成2*2即4块,每一小块上的字母都得完全相同
所以开一个ans二维数组,将每一小块的最左上角的字母作为其值,将行数是第几个块,以及列数是第几个块作为ans的第一维和第二维,如果每一小块上的字母不完全相同,那么直接输出error
最后需要输出,输出m行,列需要d块,每一个块有mm个字母
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
//typedef pair<int,int>PII;
typedef long long ll;
const int N=110;
char s[N][N];
char ans[N][N];
int n,z;
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
void solve()
{
cin>>n>>z;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>s[i][j];
}
}
if(z==100){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<s[i][j];
}
cout<<endl;
}
return;
}
if(z==200){
for(int i=0;i<2*n;i++){
for(int j=0;j<n;j++){
cout<<s[i/2][j]<<s[i/2][j];
}
cout<<endl;
}
return;
}
int m=n*z/100;
if(m*100!=n*z){
cout<<"error"<<endl;
return;
}
int d=gcd(n,m);
int nn=n/d;
int mm=m/d;
for(int i=0;i<n;i+=nn){
for(int j=0;j<n;j+=nn){
ans[i/nn][j/nn]=s[i][j];
for(int p=0;p<nn;p++){
for(int q=0;q<nn;q++){
if(s[i+p][j+q]!=ans[i/nn][j/nn]){
cout<<"error"<<endl;
return;
}
}
}
}
}
for(int i=0;i<m;i++){
for(int j=0;j<d;j++){
for(int k=0;k<mm;k++){
cout<<ans[i/mm][j];
}
}
cout<<endl;
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}