目录
🎈LeetCode 300.最长递增子序列
🎈LeetCode 674. 最长连续递增序列
🎈LeetCode 718. 最长重复子数组
🎈LeetCode 300.最长递增子序列
链接:300.最长递增子序列
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。

public int lengthOfLIS(int[] nums) {
// dp[i]表示0~i下标的最长递增子序列的长度
int[] dp=new int[nums.length];
//
for(int i=0;i<dp.length;i++){
dp[i]=1;
}
int result=1;
for(int i=1;i<nums.length;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j]){
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
result=result>dp[i]?result:dp[i];
}
return result;
}🎈LeetCode 674. 最长连续递增序列
链接:674.最长连续递增序列
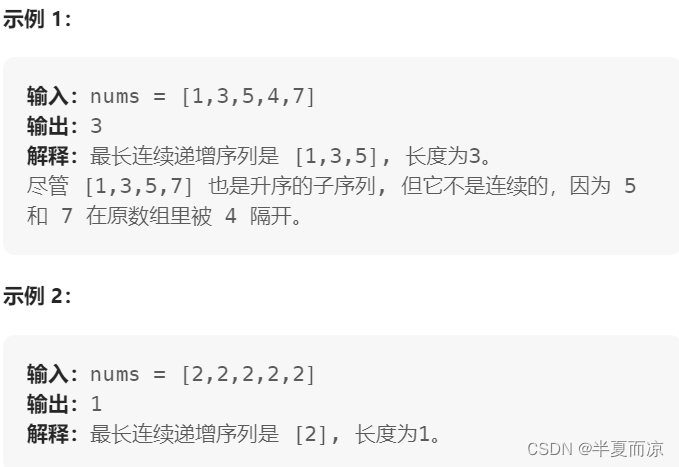
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标
l和r(l < r)确定,如果对于每个l <= i < r,都有nums[i] < nums[i + 1],那么子序列[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]就是连续递增子序列。
迭代法:比较直观
public int findLengthOfLCIS(int[] nums) {
int result=0;
int temp=1;
for(int i=1;i<nums.length;i++){
if(nums[i]>nums[i-1]){
temp++;
}else{
result=result>temp?result:temp;
temp=1;
}
}
result=result>temp?result:temp;
return result;
}动态规划法
public int findLengthOfLCIS(int[] nums) {
int[] dp=new int[nums.length];
for(int i=0;i<nums.length;i++){
dp[i]=1;
}
int result=1;
for(int i=1;i<nums.length;i++){
if(nums[i]>nums[i-1]){
dp[i]=dp[i-1]+1;
}
if(dp[i]>result){
result=dp[i];
}
}
return result;
}🎈LeetCode 718. 最长重复子数组
链接:718.最长重复子数组
给两个整数数组
nums1和nums2,返回 两个数组中 公共的 、长度最长的子数组的长度 。

public int findLength(int[] nums1, int[] nums2) {
// dp[i][j]表示0~i下标nums1和0~j下标的nums2的最长重复子数组长度
int[][] dp=new int[nums1.length+1][nums2.length+1];
int result=0;
dp[0][0]=0;
for(int i=1;i<=nums1.length;i++){
for(int j=1;j<=nums2.length;j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}
if(dp[i][j]>result){
result=dp[i][j];
}
}
}
return result;
}

![[CrackMe]Cruehead.1.exe的逆向及注册机编写](https://img-blog.csdnimg.cn/4764eed52f69487ba009f911e869420a.png)