机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索]
- 引言
- 回顾:精确搜索步长及其弊端
- 非精确搜索近似求解最优步长的条件
- 反例论述
引言
上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜索方法。
回顾:精确搜索步长及其弊端
关于线搜索方法的迭代过程表示如下:
x
k
+
1
=
x
k
+
α
k
⋅
P
k
x_{k+1} = x_k + \alpha_k \cdot \mathcal P_k
xk+1=xk+αk⋅Pk
其中:
- 变量 x k , x k + 1 ∈ { x k } k = 0 ∞ x_k,x_{k+1} \in \{x_{k}\}_{k=0}^{\infty} xk,xk+1∈{xk}k=0∞表示先搜索处理优化问题时,迭代过程中产生的数值解;
- α k \alpha_{k} αk是一个标量,表示步长信息;
-
P
k
\mathcal P_k
Pk可视作一个单位向量,描述当前迭代步骤下数值解更新的方向信息。
如果P k \mathcal P_k Pk是一个描述方向的常规向量,依然可以将其表示为”系数× \times ×单位向量“的形式,最后将系数与α k \alpha_k αk合并即可。
而基于精确搜索线搜索方法寻找最优步长的基本逻辑是:
- 固定住单位向量
P
k
\mathcal P_k
Pk,此时关于当前时刻数值解对应的目标函数
f
(
x
k
+
1
)
f(x_{k+1})
f(xk+1)可看作是仅与步长变量
α
\alpha
α相关的一个函数
ϕ
(
α
)
\phi(\alpha)
ϕ(α):
f ( x k + 1 ) = f ( x k + α ⋅ P k ) ≜ ϕ ( α ) \begin{aligned} f(x_{k+1}) = f(x_k + \alpha \cdot \mathcal P_k) \triangleq \phi(\alpha) \end{aligned} f(xk+1)=f(xk+α⋅Pk)≜ϕ(α) - 通过选择合适步长
α
k
\alpha_k
αk,使得目标函数
f
(
x
k
+
1
)
f(x_{k+1})
f(xk+1)达到最小,从而达到当前迭代步骤优化程度最大的目的:
α k = arg min α > 0 f ( x k + 1 ) \alpha_k = \mathop{\arg\min}\limits_{\alpha > 0} f(x_{k+1}) αk=α>0argminf(xk+1)
具体步骤表示如下:
对每个迭代步骤
k
=
1
,
2
,
⋯
,
∞
k=1,2,\cdots,\infty
k=1,2,⋯,∞执行如下操作:
由于此时
f
(
x
k
+
1
)
=
ϕ
(
α
)
f(x_{k+1}) = \phi(\alpha)
f(xk+1)=ϕ(α)仅包含
α
\alpha
α一个变量,因而仅需要对
ϕ
(
α
)
\phi(\alpha)
ϕ(α)求导,然后从极值中选出最小值即可。
- 关于
ϕ
(
α
)
\phi(\alpha)
ϕ(α)对
α
\alpha
α进行求导操作:
∂ ϕ ( α ) ∂ α = [ ∇ f ( x k + α ⋅ P k ) ] T ⋅ P k \frac{\partial \phi(\alpha)}{\partial \alpha} = \left[\nabla f(x_k + \alpha \cdot \mathcal P_k)\right]^T \cdot \mathcal P_k ∂α∂ϕ(α)=[∇f(xk+α⋅Pk)]T⋅Pk - 令
∂
ϕ
(
α
)
∂
α
≜
0
\begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha} \triangleq 0\end{aligned}
∂α∂ϕ(α)≜0,从而求解位于极值点的
α
\alpha
α信息,再选择使
f
(
x
k
+
1
)
f(x_{k+1})
f(xk+1)最小对应的
α
\alpha
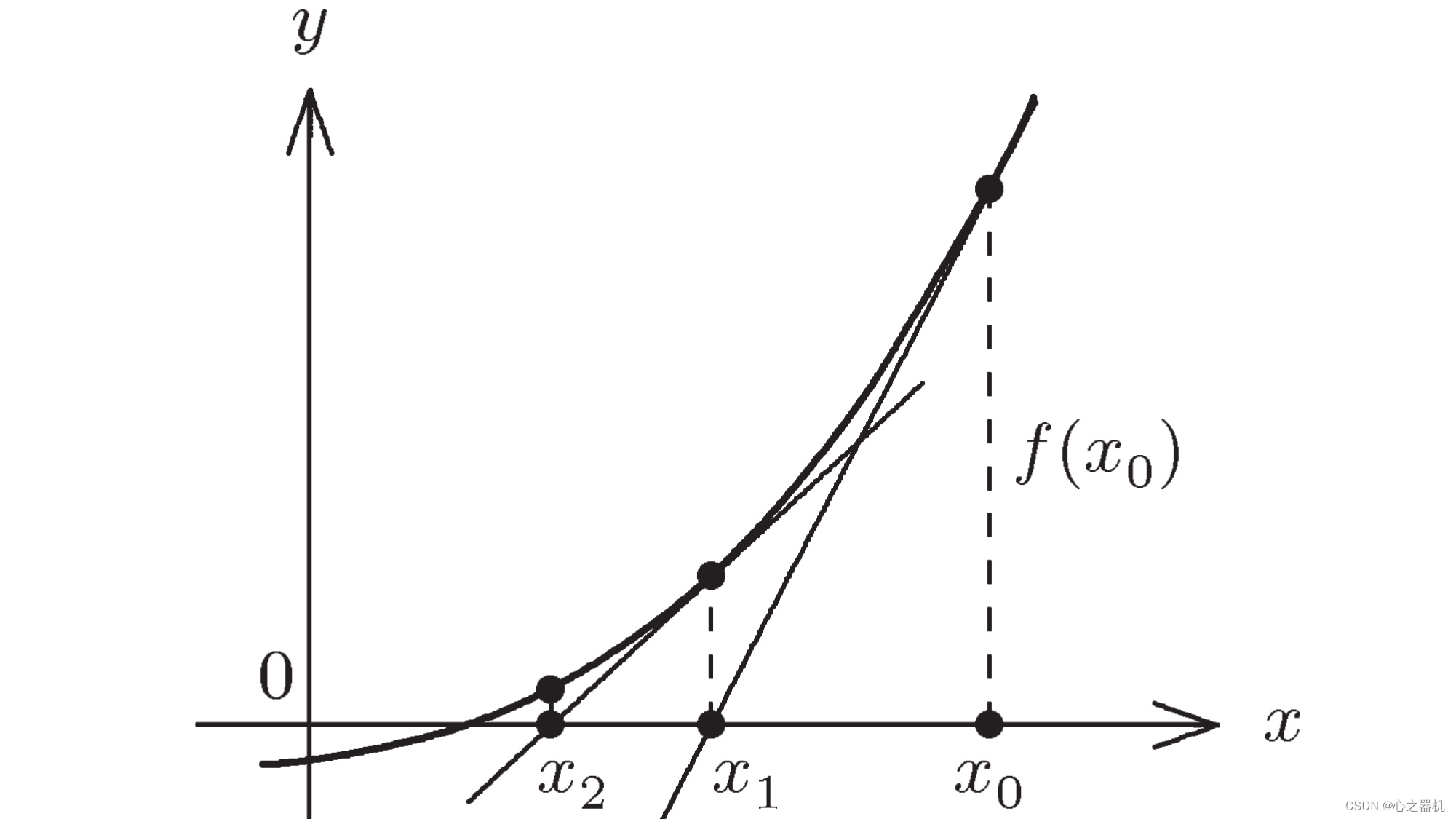
α即可,示例图像表示如下:
这仅仅是关于ϕ ( α ) \phi(\alpha) ϕ(α)的一种描述。由于我们对目标函数f ( ⋅ ) f(\cdot) f(⋅)未知,我们不能得到ϕ ( α ) \phi(\alpha) ϕ(α)精确的函数图像。唯一知道ϕ ( 0 ) = f ( x k ) \phi(0) = f(x_k) ϕ(0)=f(xk)(无法取到)且∂ ϕ ( α ) ∂ α ∣ α = 0 < 0 \begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha} |_{\alpha=0} < 0\end{aligned} ∂α∂ϕ(α)∣α=0<0,详细过程见上一节。

貌似上述流程看起来并不复杂,但在真实环境下,精确搜索参与的迭代过程可能是麻烦的:
- 首先,对于目标函数 f ( ⋅ ) f(\cdot) f(⋅)的复杂程度我们一无所知。真实环境中, f ( ⋅ ) f(\cdot) f(⋅)可能是极复杂的。这意味着: ∂ ϕ ( α ) ∂ α \begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha}\end{aligned} ∂α∂ϕ(α)可能极难表达甚至是无法表达;
- 其中求导以及获取极值的操作仅仅是一次迭代过程中的操作。若每一次迭代过程都要执行上述操作,对应的计算代价有可能极高;
- 实际上,精确求解当前迭代步骤的最优步长不是我们关注的重点,我们希望每次迭代过程中,使用较小的计算代价得到一个比较不错的步长结果,从而降低整体计算代价。
很明显,精确搜索的求解过程是一个求解析解的过程。下面我们观察如何通过求解数值解的方式对最优步长的获取过程进行优化。
非精确搜索近似求解最优步长的条件
首先思考:步长变量
α
\alpha
α需要满足什么条件,才能够使
{
f
(
x
k
)
}
k
=
0
∞
\{f(x_k)\}_{k=0}^{\infty}
{f(xk)}k=0∞收敛,并最终得到目标函数的最优解
f
∗
f^*
f∗:
{
f
(
x
k
)
}
k
=
0
∞
⇒
f
∗
\{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^*
{f(xk)}k=0∞⇒f∗
根据我们关于线搜索方法的假设,首先必然需要使
{
f
(
x
k
)
}
k
=
0
∞
\{f(x_k)\}_{k=0}^{\infty}
{f(xk)}k=0∞服从严格的单调性:
ϕ
(
α
)
=
f
(
x
k
+
1
)
<
f
(
x
k
)
=
ϕ
(
0
)
k
=
0
,
1
,
2
,
⋯
\phi(\alpha) = f(x_{k+1}) < f(x_k) = \phi(0) \quad k=0,1,2,\cdots
ϕ(α)=f(xk+1)<f(xk)=ϕ(0)k=0,1,2,⋯
新的思考:如果步长变量
α
\alpha
α仅仅满足上述条件,是否能够保证
{
f
(
x
k
)
}
k
=
0
∞
\{f(x_k)\}_{k=0}^{\infty}
{f(xk)}k=0∞最终收敛至最优解
?
?
?
答案是否定的,并且关于两个事件:
- 事件 1 1 1: ϕ ( α ) = f ( x k + 1 ) < f ( x k ) = ϕ ( 0 ) k = 0 , 1 , 2 , ⋯ \phi(\alpha) = f(x_{k+1}) < f(x_k) = \phi(0) \quad k=0,1,2,\cdots ϕ(α)=f(xk+1)<f(xk)=ϕ(0)k=0,1,2,⋯;
- 事件 2 2 2: { f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗
事件 1 1 1是事件 2 2 2的必要不充分条件。也就是说:事件 1 1 1推不出事件 2 2 2,相反,事件 2 2 2能够推出事件 1 1 1。
反例论述
这里描述一个反例:
- 假设真正的目标函数
f
(
⋅
)
f(\cdot)
f(⋅)表示如下:

可以看出,该目标函数存在最小值 − 1 -1 −1。而我们的目标是通过求数值解的方式取到 − 1 -1 −1。
- 而这个数值解仅仅受到事件
1
1
1的约束。也就是说:在迭代过程中仅满足
f
(
x
k
+
1
)
<
f
(
x
k
)
f(x_{k+1}) < f(x_k)
f(xk+1)<f(xk)即可。至此,假设:数值解
{
x
k
}
k
=
1
∞
\{x_k\}_{k=1}^{\infty}
{xk}k=1∞对应的目标函数结果
{
f
(
x
k
)
}
k
=
1
∞
\{f(x_k)\}_{k=1}^{\infty}
{f(xk)}k=1∞满足如下函数:
f ( x k ) = 5 k f(x_{k}) = \frac{5}{k} f(xk)=k5
解释:
函数 f ( x k ) = 5 k \begin{aligned} f(x_k) = \frac{5}{k}\end{aligned} f(xk)=k5是我们假设的,隐藏在背后的逻辑。而真正被我们看到的是下面由表格组成的关于 { f ( x k ) } k = 1 ∞ \{f(x_k)\}_{k=1}^{\infty} {f(xk)}k=1∞的序列信息:
其中x 0 x_0 x0是初始化的,不在函数内。这里假设x 0 = 10 x_0 = 10 x0=10,但在本示例中假设的值要> 5 = f ( x 1 ) >5 = f(x_1) >5=f(x1)。之所以要将函数设置成这种格式,是因为基于该函数产生的序列满足事件1:f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)。
| k k k | 0 ( init ) 0(\text{init}) 0(init) | 1 1 1 | 2 2 2 | 3 3 3 | ⋯ \cdots ⋯ |
|---|---|---|---|---|---|
| f ( x k ) f(x_k) f(xk) | 10 10 10 | 5 5 5 | 5 2 \begin{aligned}\frac{5}{2}\end{aligned} 25 | 5 3 \begin{aligned}\frac{5}{3}\end{aligned} 35 | ⋯ \cdots ⋯ |
至此,我们找到了一组满足事件 1 1 1的由数值解的目标函数结果构成的序列 { f ( x k ) } k = 0 ∞ = { 10 , 5 , 5 2 , 5 3 , ⋯ } \{f(x_k)\}_{k=0}^{\infty} = \left\{10,5,\begin{aligned}\frac{5}{2},\frac{5}{3},\cdots\end{aligned} \right\} {f(xk)}k=0∞={10,5,25,35,⋯},我们观察:这组序列是否能够找到目标函数最优解。
- 初始状态下,
[
x
0
,
f
(
x
0
)
=
10
]
[x_0,f(x_0) = 10]
[x0,f(x0)=10]在图中表示如下。
由于此时的梯度仅仅是一个1 1 1维向量,在函数图像中对应函数在该点上的斜率。而在横坐标上,梯度的方向仅有两个:正向(右侧;顺着坐标轴的方向);反向(逆着坐标轴的方向)。因此,图中所说的下降方向必然是最速下降方向(因为只有两个方向)。由于( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))在图中对应位置的斜率是正值,因此下一时刻更新的方向必然是负梯度方向(反向),见红色箭头。

- 观察第二个点:
[
x
1
,
f
(
x
1
)
=
5
]
[x_1,f(x_1) = 5]
[x1,f(x1)=5],对应图像表示如下:
在该目标函数中,函数值为5 5 5存在两个对应的横坐标。实际上取哪个点都不影响梯度的观察。这里为方便观察,取左侧的横坐标,后续类似情况同理。左侧点斜率是负值,因而它的负梯度方向是正向,见红色箭头。

- 同理,可以将
[
x
2
,
f
(
x
2
)
=
5
2
]
,
[
x
3
,
f
(
x
3
)
=
5
3
]
\begin{aligned} \left[x_2,f(x_2) = \frac{5}{2}\right],\left[x_3,f(x_3) = \frac{5}{3}\right]\end{aligned}
[x2,f(x2)=25],[x3,f(x3)=35]及其对应梯度方向表示在图像上:

- 以此类推。我们可以按照
{
f
(
x
k
)
}
k
=
0
∞
\{f(x_k)\}_{k=0}^{\infty}
{f(xk)}k=0∞的顺序,将梯度变化路径用红色箭头描述出来:
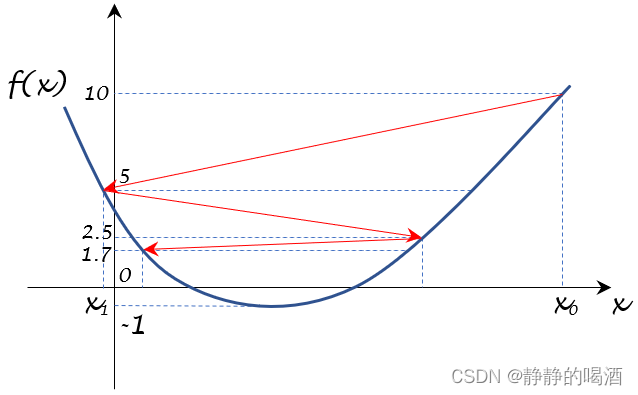
- 从上图可以看出,随着迭代次数
k
k
k的增加,我们都会产生新的点并震荡下去。但是否能够震荡到最小值呢
?
?
?这取决于:
k
→
∞
k \to \infty
k→∞时,
f
(
x
k
)
f(x_k)
f(xk)的取值结果。
lim k → ∞ f ( x k ) = 5 ∞ ≈ 0 \mathop{\lim}\limits_{k \to \infty} f(x_k) = \frac{5}{\infty} \approx 0 k→∞limf(xk)=∞5≈0
最终,它只会在 x x x轴的上方,无限地朝向 0 0 0的方向震荡,而不会越过 x x x轴,向最优值 − 1 -1 −1进行震荡。
综上,上述反例满足事件
1
1
1的条件,但它可能不会一定收敛到最优解。也就是说:仅使用
f
(
x
k
+
1
)
<
f
(
x
k
)
f(x_{k+1}) < f(x_k)
f(xk+1)<f(xk)对步长
α
\alpha
α进行判别是不可行的。
上述反例描述的是:
{
f
(
x
k
)
}
k
=
0
∞
\{f(x_k)\}_{k=0}^{\infty}
{f(xk)}k=0∞能够收敛,但没有收敛到最优解。
相关参考:
【优化算法】线搜索方法-步长-非确定性搜索