非线性优化的数值方法小结——梯度下降法，牛顿法，高斯牛顿法，LM法

在非线性优化领域中，我们常采用一系列数值方法对构造的问题进行求解，各方法彼此联系，本文将对这些数值处理方法进行梳理构造。

问题描述

非线性优化问题有很多种，本文将用最常见的非线性优化问题——也是高斯牛顿法和LM法能处理的唯一问题——最小二乘问题展开分析：
最小二乘问题，即让误差函数的绝对值最小，我们设误差函数为f(x),则我们的目标是：
$$\min F(x)=\frac{1}{2}\Vert f(x){\Vert }_2^2$$
使得F(x)最小化。如何解决这个问题呢？

梯度下降法

梯度下降法的思路是给定一个函数，在每次迭代让自变量x沿着负梯度方向前进一步，就可以让函数F(x)减小。最终函数将收敛至无法减小，也就是梯度为0的地方，也就是局部最小值。
$$F(x)=\frac{1}{2}\Vert f(x){\Vert }_2^2=\frac{1}{2}f(x{)}^{T}f(x)$$
$$F(x{)}^{\prime }=f(x{)}^{T\prime }f(x)$$
我们令$J=f(x{)}^{T\prime }$，梯度下降法的假设是让x沿着负梯度的方向运动：
$$x_{k+1}=x_k-\alpha J$$
$\alpha$是步长，常取0到1之间的值，这就是梯度下降法。另一种常用的方法最速下降法与梯度下降法形式相同，区别在于，梯度下降法中$\alpha$是人工设定的经验值，最速下降法中，$\alpha$是求解优化问题：
$${\alpha }_k={\mathrm{argmin}}_{{\alpha }_k}f\left(x_i-{\alpha }_{k}J\right)$$
计算得到的。这个优化问题怎么求呢？最直观的方法，通过二分法不断搜索${\alpha }_k$的值取最优。
性质分析
1、梯度下降法是线性收敛的，由于没有用到函数本身的信息，收敛较慢。
2、对于强凸函数，具有全局收敛性。
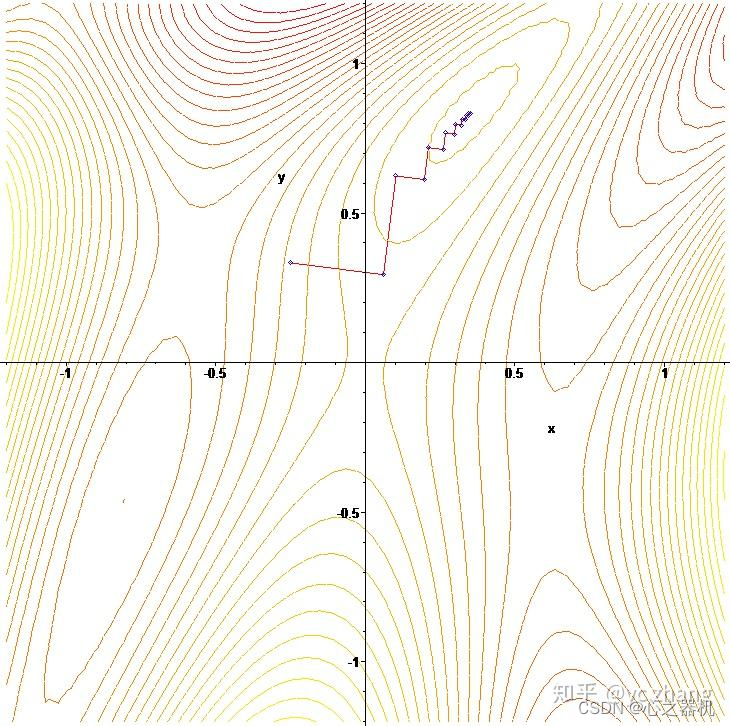
3、由于每次都朝梯度方向运动，因此轨迹常呈锯齿状：

牛顿法

牛顿法是一种用于求解方程：
$$f(x)=0$$
的方法。其思路是，对于迭代过程中的值$x_k$，过该点，沿着该点的梯度方向做直线，与横轴的交点即为$x_{k+1}$

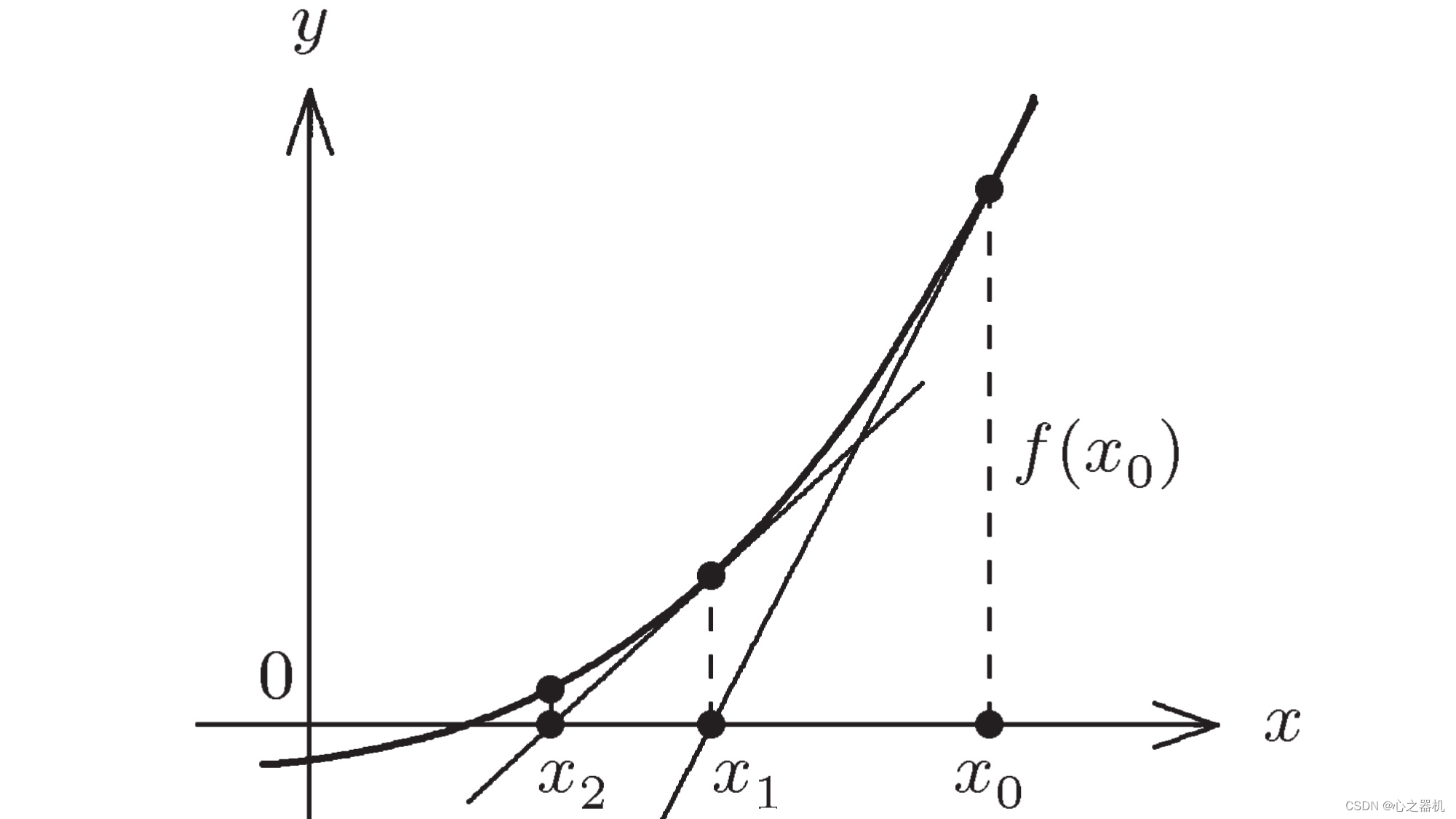
因此我们可以得到$x_k$与$x_{k+1}的关系：
$$f(x_{k+1})-f(x_k)=f(x_k{)}^{\prime }(x_{k+1}-x_k)$$
我们希望$f(x_{k+1})=0$,因此,我们对$x_{k+1}$这样取值：
$$x_{k+1}=x_k-\frac{f(x_k)}{f(x_k{)}^{\prime }}$$
牛顿法可以求解任意f(x) = 0的问题，在最小二乘问题中，我们希望得到F(x)的最小值，也就是F(x)'=0，因此，实际的迭代过程是：
$$x_{k+1}=x_k-\frac{F(x_k{)}^{\prime }}{F(x_k{)}^{\prime \prime }}=x_k-\frac{Jf(x_k)}{f(x_k{)}^{\prime \prime }+J{J}^T}$$
在多维情况下，我们一般称$f(x_k{)}^{\prime \prime }$为海森矩阵H，也就是：
$$x_{k+1}=x_k-\frac{Jf(x_k)}{H+J{J}^T}$$
要注意，很多博主这块自己没弄清楚，海森矩阵和$J{J}^T$分不清，F(x)和f(x)分不清，导致一些模棱两可的推导。
性质分析
1、牛顿法需要求海森矩阵，在高维和规模较大的情况下计算量大，一般避免求海森矩阵。
2、牛顿法在最优点附近具有二次收敛性，比梯度法有快的多。但是，其代价是只具有局部收敛性，当初值远离最优点时，即便函数是凸的，依然有可能无解。

高斯牛顿法

从方法的名字也可以看出高斯牛顿法是高斯在牛顿法的基础上改进的，高斯发现，除了能对F(x)直接展开优化，还可以对f(x)做文章，于是他先将f(x)展开：

$$f(x+\Delta x)=f(x)+J\Delta x+o(\Delta x)$$
我们可以求变量$\Delta x$的最优值来让F(x)最小：
$$G(\Delta x)=F(x+\Delta x)=\frac{1}{2}\Vert f(x+\Delta x){\Vert }_2^2=\frac{1}{2}f(x+\Delta x{)}^{T}f(x+\Delta x)$$
$$=\frac{1}{2}(f(x)+J\Delta x{)}^T(f(x)+J\Delta x)=\frac{1}{2}f(x{)}^{T}f(x)+f(x)J\Delta x+\Delta x^T{J}^{T}J\Delta x$$
该函数对\Delta x求导，得：
$$G(\Delta x{)}^{\prime }=Jf(x)+J^{T}J\Delta x$$
当$G(\Delta )x^{\prime }=0$时，F(x+\Delta x) 取值达到了最小。因此，我们令：
$$\Delta x=-\frac{Jf(x)}{J^{T}J}$$

有人也把$J^{T}J$写作$H$，要注意这里的H并非海森矩阵。
性质分析
1、高斯牛顿法最大的改进在于不需要求海森矩阵，减少了计算量。
2、$J^{T}J$只能保证半正定，而其作为分母时需要是正定的。这导致算法可能出现奇异或接近奇异时稳定性差
3、和牛顿法的收敛性一样，高斯牛顿法也有局部二阶收敛性。
4、当求解出的步长$\Delta x$太大时，会导致局部近似不精确，甚至不收敛。牛顿法也有类似问题。

LM（列文伯格-马夸特）法

为了解决高斯牛顿法的不收敛性问题（顺便解决了歧义性问题），又诞生了LM方法。LM方法的核心思路是，引入一个迭代步长的信赖域$\mu$，认为当$\Delta x<\mu$时，这次迭代才是可以信赖的。即：
$$\min F(x)=min\frac{1}{2}\Vert f(x)+J\Delta x\Vert \text{ s.t }\Vert D\Delta x<\mu {\Vert }_2$$
用拉格朗日法，将有约束问题转化为无约束问题：
$$L(\Delta x,\lambda )=\frac{1}{2}{\Vert f(x)+J\Delta x\Vert }^2+\frac{\lambda }{2}\left(\Vert D\Delta x{\Vert }^2-\mu \right)$$
求导并让导数为0，有：
$$\left(J{J}^T+\lambda D^{T}D\right)\Delta x=-Jf(x)$$
我们把$J^{T}J$写作$H$，令D取单位矩阵I得：

$$\Delta x=-\frac{Jf(x)}{H+\lambda I}$$
在实际使用中\lambda 是通过迭代计算得到的值。我们发现，当\lambda较小时，该方法和高斯牛顿法相同，当lambda较大时，$\Delta x=-\frac{Jf(x)}{\lambda }$，和梯度下降法形式i相同。可以认为LM方法是梯度方法和高斯牛顿法的结合，那么$\lambda$如何计算呢？
一般，我们取一个较小的处置${\lambda }_0$,之后进行迭代，我们需要计算这次迭代的近似效果（也就是信赖程度）：
$$\rho =\frac{f(x+\Delta x)-f(x)}{J^T\Delta x}$$
当$\rho$较大时，表示这次拟合程度较好，可以适当扩大信赖域，当$\rho$较小时，表示拟合程度较差，需要缩小信赖域。
性质分析
1、LM法通过添加阻尼项（信赖域项），控制了$\Delta x$的大小，解决了高斯牛顿法收敛性差的问题。
2、阻尼项也解决了奇异的问题，保证了分母的正定性。