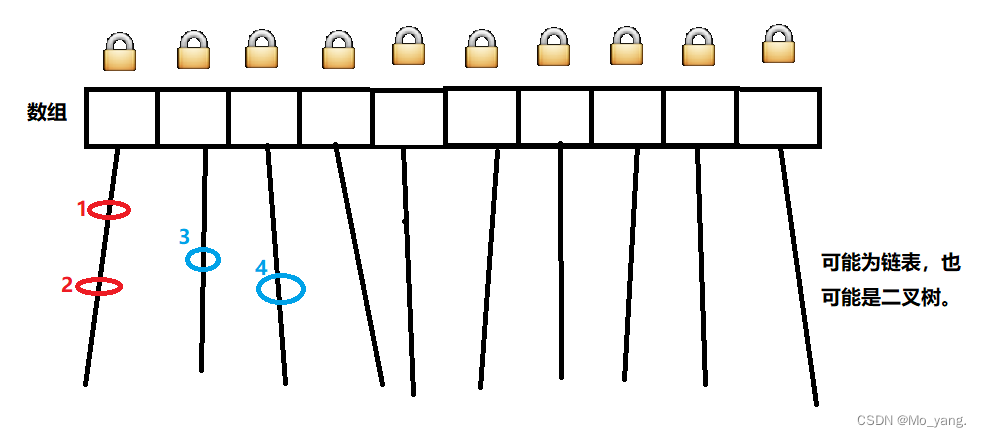
二叉树的最大深度：

 

class Solution {
public:
    int maxDepth(TreeNode* root) {
        //DFS 深度优先搜索
        if(root==NULL) return 0;
        //深度等于max（左子树的深度，右子树的深度）+1；
        return max(maxDepth(root->left),maxDepth(root->right))+1;



        //BFS 广度优先搜索  借助队列来实现
        queue<TreeNode*> qq;
        qq.push(root);//先将根节点入队
        while(!qq.empty())
        {
            TreeNode* node=qq.front();//保存队头元素
            qq.pop();//删除队头元素
            if(node->left||node->right)//左右子树不同时为空
            {
                len++;//深度+1
                if(node->left==NULL)//左节点为空，说明右节点不为空
                    qq.push(node->right);//右节点入队
                if(node->right==NULL)//同理
                    qq.push(node->left);
            }
        }
        return len;//返回深度
    }
};

二叉树的最小深度：

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

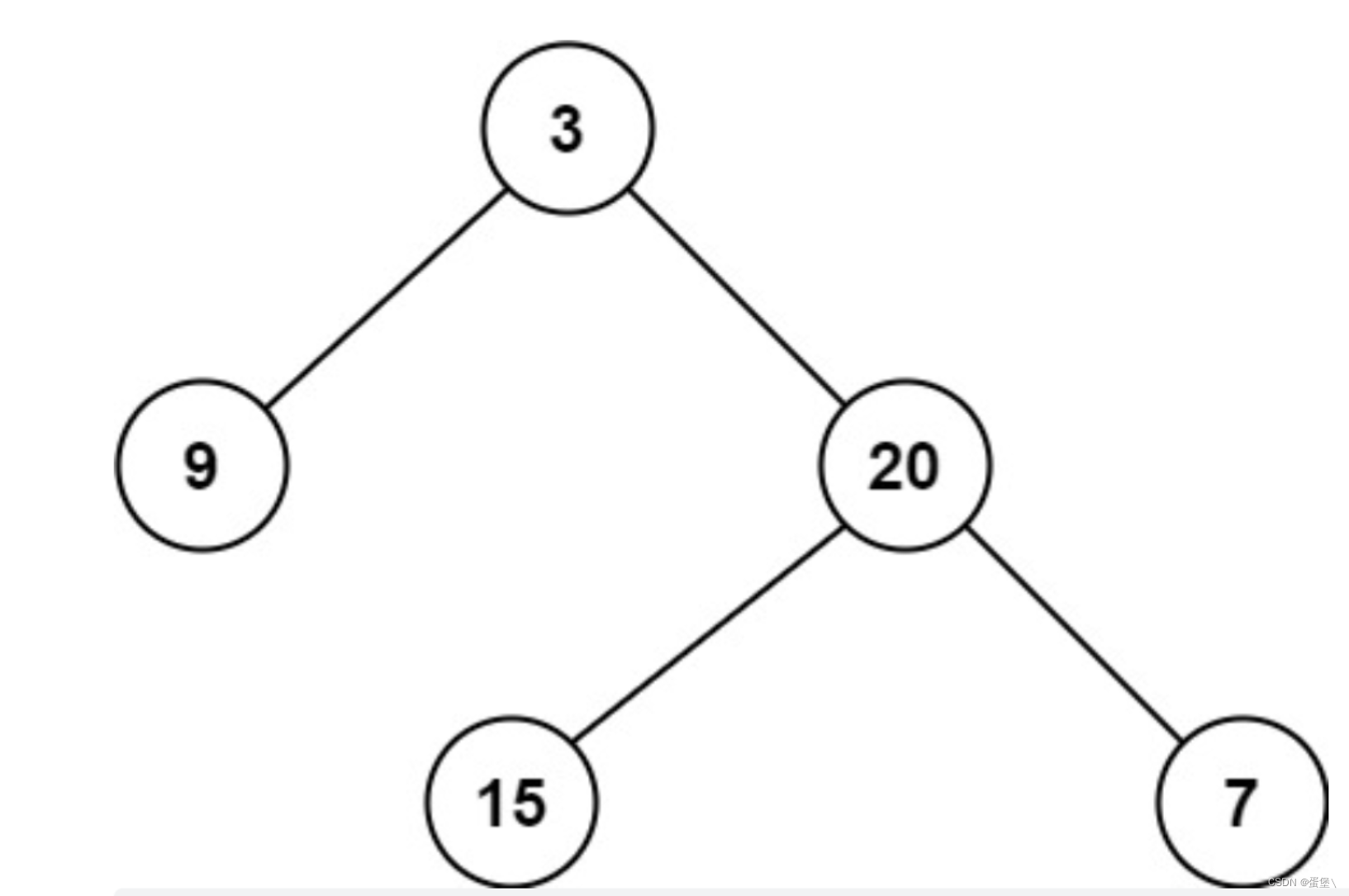
 输入：root = [3,9,20,null,null,15,7]
输出：2

 

//递归
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==nullptr) return 0;//根节点为空，直接返回深度为0
        //根节点的左右节点同时为空，深度为1
        if(root->left==nullptr&&root->right==nullptr) return 1;
        int min_depth=INT_MAX;//定义一个最小深度，初始值为最大值
        //递归的找左子树的最小深度
        if(root->left!=nullptr)
        {
            min_depth=min(minDepth(root->left),min_depth);
        }
        //递归的找右子树的最小深度  
        if(root->right!=nullptr)
        {
            min_depth=min(minDepth(root->right),min_depth);
        }
        //返回最小深度，+1是因为一开始没算根节点
        return min_depth+1;
    }
};


//迭代法
//在计算深度的基础上，找最小深度，只需加一个条件：当左右子节点同时为空时，循环结束
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==nullptr) return 0;
        queue<TreeNode*> qq;
        qq.push(root);
        int len=1;//根节点已经算上了，最后返回结果就不用再+1了
        while(!qq.empty())
        {
            int size=qq.size();
            while(size)
            {
                TreeNode* node=qq.front();
                qq.pop();
                if(node->left==nullptr && node->right==nullptr)
                {
                    break;
                }
                else
                {
                    if(node->left!=nullptr)
                        qq.push(node->left);
                    if(node->right!=nullptr)
                        qq.push(node->right);
                }   
                size--;
            }
            //判断上面的循环是正常结束，还是非正常结束
            //如果是正常结束size=0，非正常结束说明遇到了左右子节点同时为空的情况，那么就已经找到了最小深度，继续跳出当前的while循环即可。
            if(size!=0)
            {
                break;
            }
            //每遍历完一层，深度+1
            len++;
        }
        return len;
    }
};