- 使用混合高斯模型 GMM,计算如下数据点的聚类过程:
Data=np.array([1,2,6,7])
均值初值为:
μ1,μ2=1,5
权重初值为:
w1,w2=0.5,0.5
方差:
std1,std2=1,1
K=2
10 次迭代后数据的聚类标签是多少?
采用python代码实现: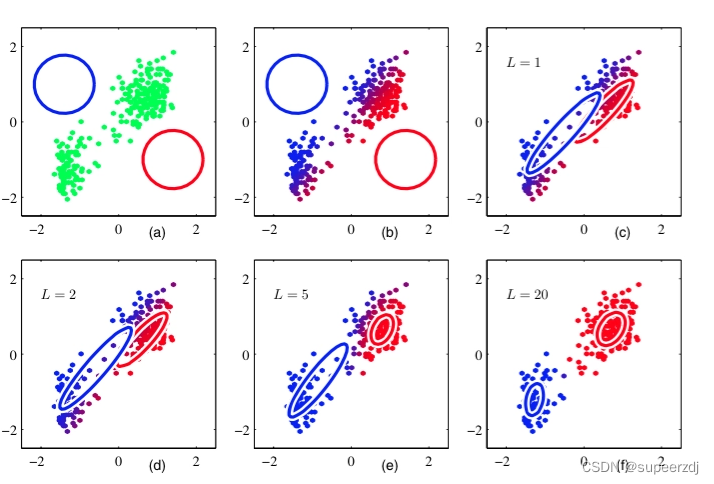
from scipy import stats
import numpy as np
#初始化数据
Data = np.array([1,2,6,7])
w1 , w2 = 0.5, 0.5
mu1 , mu2 = 1, 5
std1 , std2 = 1, 1
n = len(Data) # 样本长度
zij=np.zeros([n,2])
for t in range(10):
# E-step 依据当前参数,计算每个数据点属于每个子分布的概率
z1_up = w1 * stats.norm(mu1 ,std1).pdf(Data)
z2_up = w2*stats.norm(mu2 , std2).pdf(Data)
z_all = (w1*stats.norm(mu1 ,std1).pdf(Data)+w2*stats.norm(mu2 ,std2).pdf(Data))+0.001
rz1 = z1_up/z_all # 为甲分布的概率
rz2 = z2_up/z_all # 为乙分布的概率
# M-step 依据 E-step 的结果,更新每个子分布的参数。
mu1 = np.sum(rz1*Data)/np.sum(rz1)
mu2 = np.sum(rz2*Data)/np.sum(rz2)
std1 = np.sum(rz1*np.square(Data-mu1))/np.sum(rz1)
std2 = np.sum(rz2*np.square(Data-mu2))/np.sum(rz2)
w1 = np.sum(rz1)/n
w2 = np.sum(rz2)/n
for i in range(n):
zij[i][0] = rz1[i]/(rz1[i]+rz2[i])
zij[i][1] = rz2[i]/(rz1[i]+rz2[i])
labels = np.argmax(zij, axis=1)#输出每一行的最大值,0或1 axis表示返回每一行中最大值所在列的索引
print(labels)
聚类标签输出结果:[0 0 1 1]
也就是说,10 次迭代后数据的聚类标签是1,2归为0类6,7归为1类
附注:
如果 axis 为 None,那么 np.argmax 会将数组展平为一维,然后返回最大值的索引。例如:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.argmax(a) 3如果 axis 为 0,那么 np.argmax 会沿着第一个维度(行)进行最大值的查找,返回每一列中最大值所在的行索引。例如:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.argmax(a, axis=0) array([1, 1])如果 axis 为 1,那么 np.argmax 会沿着第二个维度(列)进行最大值的查找,返回每一行中最大值所在的列索引。例如:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.argmax(a, axis=1) array([1, 1])在之前问题中,np.argmax([gamma1, gamma2], axis=0) 的意思是沿着第一个维度(gamma1 和 gamma2)进行最大值的查找,返回每个数据点属于哪个子分布的概率更大。
-
假设我们的数据集有 10 个 3 维数据, 需要用 PCA 降到 2 维特征。
array([ [ 3.25, 1.85, -1.29], [ 3.06, 1.25, -0.18], [ 3.46, 2.68, 0.64], [ 0.3 , -0.1 , -0.79], [ 0.83, -0.21, -0.88], [ 1.82, 0.99, 0.16], [ 2.78, 1.75, 0.51], [ 2.08, 1.5 , -1.06], [ 2.62, 1.23, 0.04], [ 0.83, -0.69, -0.61]])给出求解过程
解:
- 对所有的样本进行中心化:
x(i)=x(i)−1m∑j=1mx(j)
得到:
X=np.array([
[ 1.147 0.825 -0.944]
[ 0.957 0.225 0.166]
[ 1.357 1.655 0.986]
[-1.803 -1.125 -0.444]
[-1.273 -1.235 -0.534]
[-0.283 -0.035 0.506]
[ 0.677 0.725 0.856]
[-0.023 0.475 -0.714]
[ 0.517 0.205 0.386]
[-1.273 -1.715 -0.264]])
- 计算样本的协方差矩阵 XXT
covM2=np.array([[1.26344556 1.08743889 0.32030889],
[1.08743889 1.11076111 0.31611111],
[0.32030889 0.31611111 0.45449333]])
- 对矩阵 XXT 进行特征值分解
取出最大的 n′ 个特征值对应的特征向量 (w1,…,wn′), 将所有的特征向量标准化后,组成特征向量矩阵 W。
3.1求出特征值:
eigval=np.array([2.38219729 0.09637041 0.35013229])
3.2特征向量标准化:
eigvec=np.array([
[ 0.71144 0.67380165 -0.19961077],
[ 0.66498574 -0.73733944 -0.11884665],
[ 0.22725997 0.04818606 0.97264126]])
3.3取出特征值最大的2个特征值索引,也就是[2.38,0.35]对应的第1列和第3列:
indexes=[2 0]
3.4特征向量矩阵W:(对eigvec取了第3列和第1列)
W=np.array([
[-0.19961077 0.71144 ],
[-0.11884665 0.66498574],
[ 0.97264126 0.22725997]])
- 对样本集中的每一个样本 x(i) , 转化为新的样本 z(i)=WTx(i) ,得到输出样本集 D=(z(1),…z(m))
X:3×10 W:3×2 x⋅W=10×33×2 因为输入行列转置,结果是一致的
D=np.array([
[-1.24517539 1.15010151]
[-0.05630956 0.86819503]
[ 0.49146125 2.29005381]
[ 0.06174799 -2.1317387 ]
[-0.1185103 -1.84827733]
[ 0.55280596 -0.10961848]
[ 0.6112806 1.15829407]
[-0.74632697 0.13724149]
[ 0.24787719 0.5918589 ]
[ 0.20114923 -2.10611029]])
代码:
import numpy as np
X=np.array([
[ 3.25, 1.85, -1.29],
[ 3.06, 1.25, -0.18],
[ 3.46, 2.68, 0.64],
[ 0.3 , -0.1 , -0.79],
[ 0.83, -0.21, -0.88],
[ 1.82, 0.99, 0.16],
[ 2.78, 1.75, 0.51],
[ 2.08, 1.5 , -1.06],
[ 2.62, 1.23, 0.04],
[ 0.83, -0.69, -0.61]])
def pca(X, d):
# Centralization中心化
means = np.mean(X, 0)
X = X - means
print(X)
# Covariance Matrix 计算样本协方差矩阵
M=len(X)
X=np.mat(X)
covM2=np.cov(X.T)
# 求出特征值,特征值分解
eigval , eigvec = np.linalg.eig(covM2)
indexes = np.argsort(eigval)[-d:]
W = eigvec[:, indexes]
return X*W
print(pca(X, 2))
附注:
np.cov()是一个用于计算协方差矩阵的函数,它可以接受一个或两个数组作为参数,返回一个二维数组,表示协方差矩阵。
协方差矩阵是一个对称矩阵,它的对角线元素表示各个变量的方差,非对角线元素表示两个变量之间的协方差。协方差反映了两个变量的线性相关程度,如果协方差为正,说明两个变量正相关;如果协方差为负,说明两个变量负相关;如果协方差为零,说明两个变量无相关性。
np.cov()的用法如下:
np.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None)参数说明:
- m: 一个一维或二维的数组,表示多个变量和观测值。如果是一维数组,表示一个变量的观测值;如果是二维数组,每一行表示一个变量,每一列表示一个观测值。
- y: 可选参数,另一个一维或二维的数组,表示另一组变量和观测值,必须和m具有相同的形状。
- rowvar: 可选参数,布尔值,默认为True。如果为True,表示每一行代表一个变量;如果为False,表示每一列代表一个变量。
- bias: 可选参数,布尔值,默认为False。如果为False,表示计算无偏协方差(除以n-1);如果为True,表示计算有偏协方差(除以n)。
- ddof: 可选参数,整数,默认为None。如果不为None,则覆盖由bias隐含的默认值。ddof=0表示计算有偏协方差;ddof=1表示计算无偏协方差。
- fweights: 可选参数,一维数组或整数,默认为None。表示每次观测的频率权重。
- aweights: 可选参数,一维数组,默认为None。表示每个变量的可靠性权重。
返回值:
- 一个二维数组,表示协方差矩阵。
举例说明:
import numpy as np # 生成两组随机数据 x = np.random.randn(10) y = np.random.randn(10) # 计算x和y的协方差矩阵 cov_xy = np.cov(x,y) print(cov_xy) # 输出: [[ 0.8136679 -0.01594772] [-0.01594772 0.84955963]] # 计算x和y的相关系数矩阵 corr_xy = np.corrcoef(x,y) print(corr_xy) # 输出: [[ 1. -0.01904402] [-0.01904402 1. ]]