前置内容
课程内容
- 一、由一道算法题引发的思考
- - 1.算法题
  - 2.什么是归并排序法
- 二、什么是Fork/Join框架
- - 1.基本介绍
  - 2.ForkJoinPool
  - 2.ForkJoinPool构造函数及参数解读
  - 3.任务提交方式
  - 4.工作原理图
  - 5.工作窃取
  - 6.和普通线程池之间的区别
  - 7.ForkJoinTask
学习总结

前置内容

Q1：在并发编程里面，通常我们遇到的任务类型都有哪些？
答：通常有：计算密集型（CPU密集型）、IO密集型

Q2：它们有什么区别？
答：计算密集型任务的特点是要进行大量的计算，消耗CPU资源，比如计算圆周率、对视频进行高清解码等等，全靠CPU的运算能力。这种计算密集型任务虽然也可以用多任务完成，但是任务越多，花在任务切换的时间就越多，CPU执行任务的效率就越低，所以，要最高效地利用CPU，计算密集型任务同时进行的数量应当等于CPU的核心数。
计算密集型任务由于主要消耗CPU资源，因此，代码运行效率至关重要。Python这样的脚本语言运行效率很低，完全不适合计算密集型任务。对于计算密集型任务，最好用C语言编写。
IO密集型，涉及到网络、磁盘IO的任务都是IO密集型任务，这类任务的特点是CPU消耗很少，任务的大部分时间都在等待IO操作完成（因为IO的速度远远低于CPU和内存的速度）。对于IO密集型任务，任务越多，CPU效率越高，但也有一个限度。常见的大部分任务都是IO密集型任务，比如Web应用。
IO密集型任务执行期间，99%的时间都花在IO上，花在CPU上的时间很少，因此，用运行速度极快的C语言替换用Python这样运行速度极低的脚本语言，完全无法提升运行效率。对于IO密集型任务，最合适的语言就是开发效率最高（代码量最少）的语言，脚本语言是首选，C语言最差。

课程内容

一、由一道算法题引发的思考

1.算法题

有一道算法题，题目为：【如何充分利用多核CPU的性能，快速对一个2千万大小的数组进行排序？】
说到排序算法，我估计大家多少会有点印象的，毕竟很多面试都会偶尔问到。比如有：冒泡排序啦，选择排序啦，快速排序等等。但是在这个2KW的体量下，显然是不适用的。或许更有经验一点的朋友们想到了一个办法了，那就是：归并排序法。
是的，这里就是我想引出的一个东西【归并排序法】。

2.什么是归并排序法

归并排序（Merge Sort）是一种基于分治思想的排序算法。归并排序的基本思想是将一个大数组分成
两个相等大小的子数组，对每个子数组分别进行排序，然后将两个子数组合并成一个有序的大数组。
因为常常使用递归实现(由先拆分后合并的性质决定的)，所以我们称其为归并排序。
归并排序的步骤包括以下3个：

将数组分成两个子数组
对每个子数组进行排序
合并两个有序的子数组

归并排序的时间复杂度为O(nlogn)，空间复杂度为O(n)，其中n为数组的长度。
当然，还有一个更学术一点的解释：

分治思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题
性质相同。求出子问题的解，就可得到原问题的解。
分治思想的步骤如下：

分解：将要解决的问题划分成若干规模较小的同类问题；
求解：当子问题划分得足够小时，用较简单的方法解决；
合并：按原问题的要求，将子问题的解逐层合并构成原问题的解。
计算机十大经典算法中的归并排序、快速排序、二分查找都是基于分治思想实现的算法
分治任务模型图如下：

这里用归并排序算法，简单实现了一下这个算法题，代码如下：

public class MergeSort {

    private final int[] arrayToSort; //要排序的数组
    private final int threshold;  //拆分的阈值，低于此阈值就不再进行拆分

    public MergeSort(final int[] arrayToSort, final int threshold) {
        this.arrayToSort = arrayToSort;
        this.threshold = threshold;
    }

    /**
     * 排序
     * @return
     */
    public int[] sequentialSort() {
        return sequentialSort(arrayToSort, threshold);
    }

    public static int[] sequentialSort(final int[] arrayToSort, int threshold) {
        //拆分后的数组长度小于阈值，直接进行排序
        if (arrayToSort.length < threshold) {
            //调用jdk提供的排序方法
            Arrays.sort(arrayToSort);
            return arrayToSort;
        }

        int midpoint = arrayToSort.length / 2;
        //对数组进行拆分
        int[] leftArray = Arrays.copyOfRange(arrayToSort, 0, midpoint);
        int[] rightArray = Arrays.copyOfRange(arrayToSort, midpoint, arrayToSort.length);
        //递归调用
        leftArray = sequentialSort(leftArray, threshold);
        rightArray = sequentialSort(rightArray, threshold);
        //合并排序结果
        return merge(leftArray, rightArray);
    }

    public static int[] merge(final int[] leftArray, final int[] rightArray) {
        //定义用于合并结果的数组
        int[] mergedArray = new int[leftArray.length + rightArray.length];
        int mergedArrayPos = 0;
        int leftArrayPos = 0;
        int rightArrayPos = 0;
        while (leftArrayPos < leftArray.length && rightArrayPos < rightArray.length) {
            if (leftArray[leftArrayPos] <= rightArray[rightArrayPos]) {
                mergedArray[mergedArrayPos] = leftArray[leftArrayPos];
                leftArrayPos++;
            } else {
                mergedArray[mergedArrayPos] = rightArray[rightArrayPos];
                rightArrayPos++;
            }
            mergedArrayPos++;
        }

        while (leftArrayPos < leftArray.length) {
            mergedArray[mergedArrayPos] = leftArray[leftArrayPos];
            leftArrayPos++;
            mergedArrayPos++;
        }

        while (rightArrayPos < rightArray.length) {
            mergedArray[mergedArrayPos] = rightArray[rightArrayPos];
            rightArrayPos++;
            mergedArrayPos++;
        }

        return mergedArray;
    }

    public static void main(String[] args) {

        // 初始化一个2KW的数组
        Random random = new Random();
        int[] arrays = new int[20000000];
        for (int i = 0; i < 20000000; i++) {
            arrays[i] = random.nextInt(5);
        }


        long start1 = System.currentTimeMillis();

        // 开始拆分排序
        MergeSort mergeSort = new MergeSort(arrays, 100000);
        mergeSort.sequentialSort();
        System.out.println("任务总耗时：wasteTime=" + (System.currentTimeMillis() - start1));
    }
//    系统输出：
//    任务总耗时：wasteTime=921
}

可以看出来，总共的耗时是：921ms（这还是我的电脑相对较好）
我想大家都看出来了，这里921ms看似不错的，那如果这个数据规模再大一点又会怎样呢？可以很负责的告诉大家，那时候就不是简单累加了，可能是指数型增长。而且细心的朋友可能已经看出来了，上面的代码完全是在单线程环境下运行（完全就是1核负重前行，其他核在岁月静好，不能忍），有没有可能，多线程环境下，运行效果会更好呢？
我们知道，我们无论做了什么优化，其实很多目的都是为了尽可能地压榨CPU资源的，像我们很多电脑一样，很多时候CPU使用率都是极低的，于是在一些大牛眼里，这样的行为非常浪费资源（/狗头/狗头）。如下图：13%的CPU使用率，资本家看了都在叹气，何其浪费啊
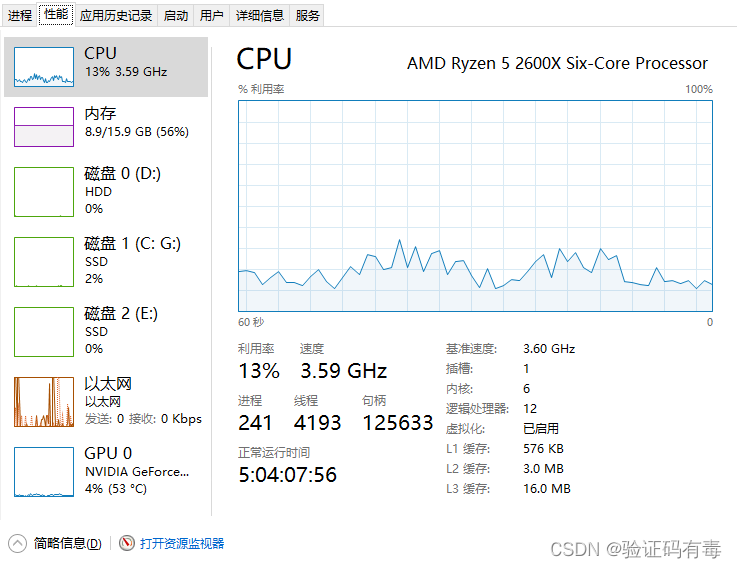
在这里插入图片描述
于是，大牛们为了解决上面说的【1核负重前行，其他核在岁月静好】的不公平现象，提出了一种新的线程池，ForkJoinPool（相信大家会有疑问：线程池？那为啥不用之前的ThreadPoolExecutor？别急，下面会给大家解释）

二、什么是Fork/Join框架

1.基本介绍

Fork/Join 框架是 Java7 提供了的一个用于并行执行任务的框架，是一个把大任务分割成若干个小任务，最终汇总每个小任务结果后得到大任务结果的框架（分治思想）。（Fork，刀叉的意思；join，连接的意思。用叉子把某个东西分开，然后最后又连接起来）
Fork 就是把一个大任务切分为若干子任务并行的执行，Join 就是合并这些子任务的执行结果，最后得到这个大任务的结果。比如计算1+2+ ...＋20000000，可以分割成 10 个子任务，每n个子任务分别对 2000000 个数进行求和，最终汇总这 10 个子任务的结果。如下图所示：
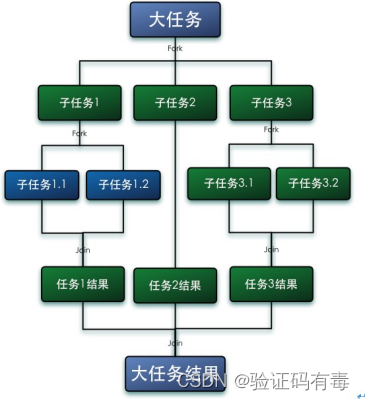
在这里插入图片描述

2.ForkJoinPool

ForkJoinPool是Fork/Join框架中的线程池类，它用于管理Fork/Join任务的线程。跟ThreadPoolExecutor一样，它也是继承于AbstractExecutorService类，所以它跟ThreadPoolExecutor相同的行为，例如submit()、invoke()、shutdown()、awaitTermination()等，用于提交任务、执行任务、关闭线程池和等待任务的执行结果。ForkJoinPool类中还包括一些参数，例如线程池的大小、工作线程的优先级、任务队列的容量等，可以根据具体的应用场景进行设置。类图如下：
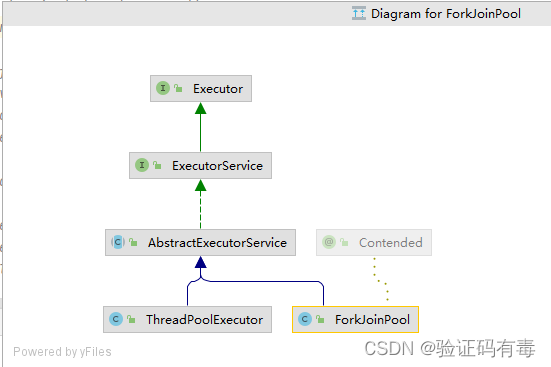
在这里插入图片描述

它具有以下特性：

ForkJoinPool 不是为了替代 ExecutorService，而是它的补充，在某些应用场景下性能比 ExecutorService 更好；
ForkJoinPool 主要用于实现“分而治之”的算法，特别是分治之后递归调用的函数，例如 quick sort 等；
ForkJoinPool 最适合的是计算密集型的任务，如果存在 I/O，线程间同步，sleep() 等会造成线程长时间阻塞的情况时，最好配合使用 ManagedBlocker。

就像上面说的，ForkJoinPool是ThreadPoolExecutor的补充，前者适合于计算密集型任务，所以后者通常就是适合IO密集型任务了。

2.ForkJoinPool构造函数及参数解读

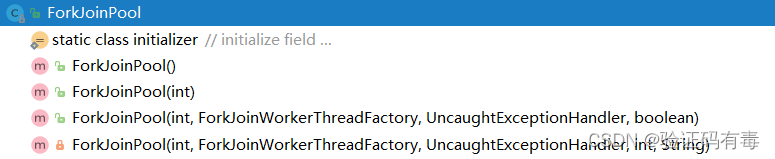
在这里插入图片描述

public ForkJoinPool(int parallelism,
                        ForkJoinWorkerThreadFactory factory,
                        UncaughtExceptionHandler handler,
                        boolean asyncMode)

如上面代码所示，ForkJoinPool中有4个核心参数，分别用于：控制线程池的并行数、工作线程的创建、异常处理和指定队列模式等。各参数解释如下：

int parallelism：指定并行级别（parallelism level）。ForkJoinPool将根据这个设定，决定工作线程的数量。如果未设置的话，将使用Runtime.getRuntime().availableProcessors()来设置并行级别；
ForkJoinWorkerThreadFactory factory：ForkJoinPool在创建线程时，会通过factory来创建。注意，这里需要实现的是ForkJoinWorkerThreadFactory，而不是ThreadFactory。如果你不指定factory，那么将由默认的DefaultForkJoinWorkerThreadFactory负责线程的创建工作；
UncaughtExceptionHandler handler：指定异常处理器，当任务在运行中出错时，将由设定的处理器处理；
boolean asyncMode：设置队列的工作模式。当asyncMode为true时，将使用先进先出队列，而为false时则使用后进先出的模式。

3.任务提交方式

任务提交是ForkJoinPool的核心能力之一，提交任务有三种方式：
在这里插入图片描述

4.工作原理图

还记得下面这张图吗，ThreadPoolExecutor的工作原理图：
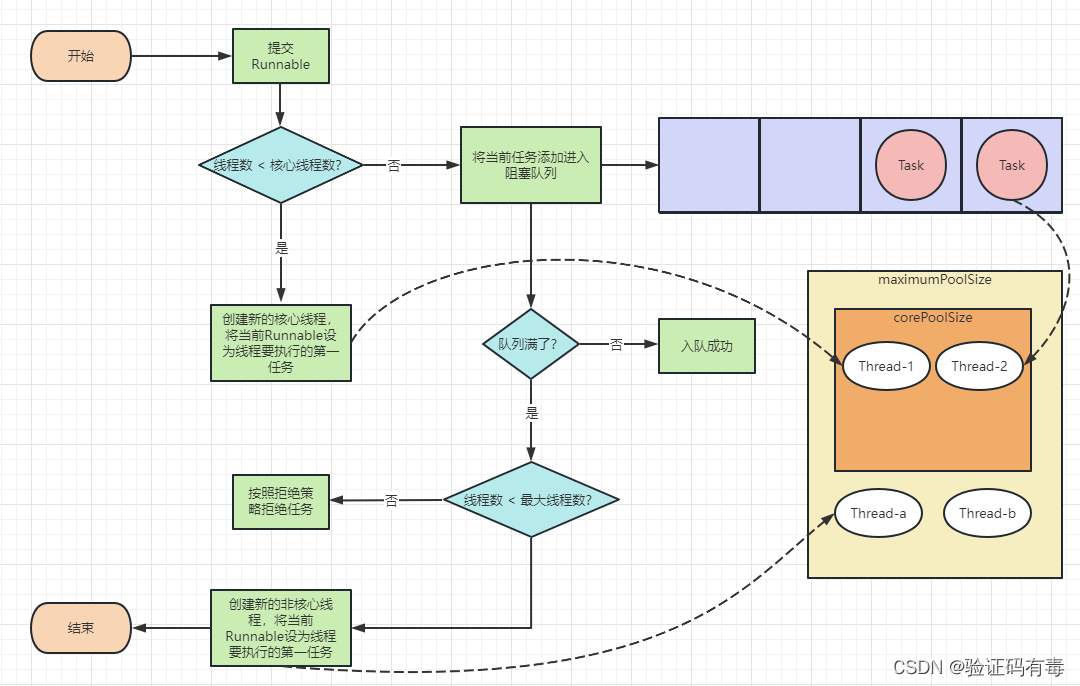
在这里插入图片描述
ForkJoinPool与ThreadPoolExecutor不一样，它为了适应更大的并行度，对工作队列的设计做了改造。它的原理图如下：

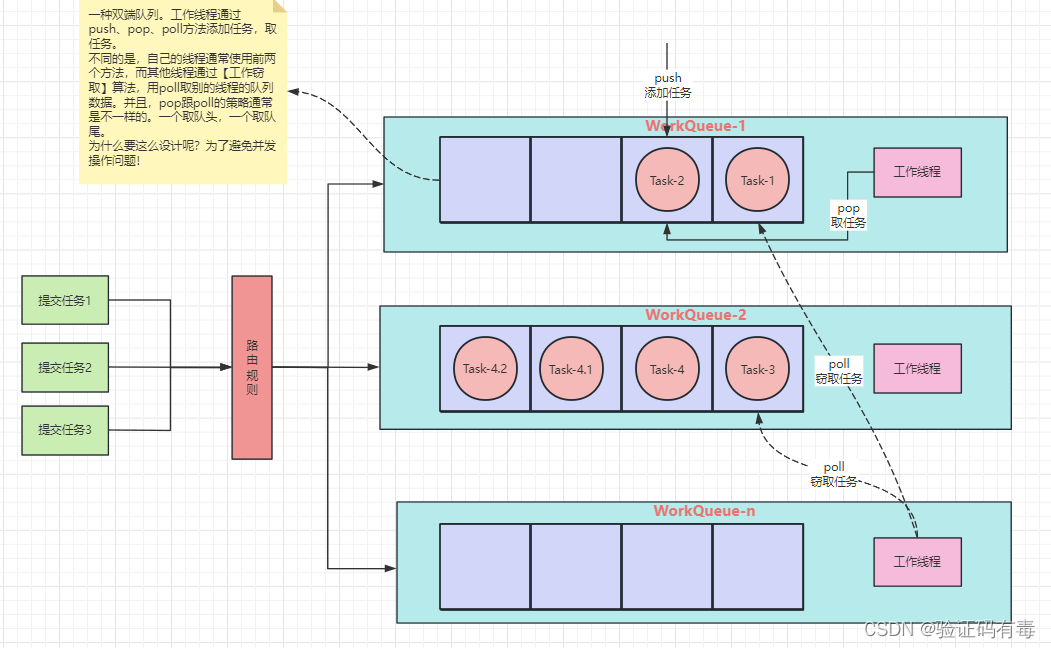
ForkJoinPool 内部有多个任务队列，当我们通过 ForkJoinPool 的 invoke() 或者 submit() 方法提交任务时，ForkJoinPool 根据一定的路由规则把任务提交到一个任务队列中，如果任务在执行过程中会创建出子任务，那么子任务会提交到工作线程对应的任务队列中（如上图中的Task-4，通过fork方法继续分出了Task-4.1和Task-4.2）。
如果工作线程对应的任务队列空了，是不是就没活儿干了呢？不是的，ForkJoinPool 支持一种叫做【任务窃取】的机制，如果工作线程空闲了，那它可以“窃取”其他工作任务队列里的任务。如此一来，所有的工作线程都不会闲下来了。

5.工作窃取

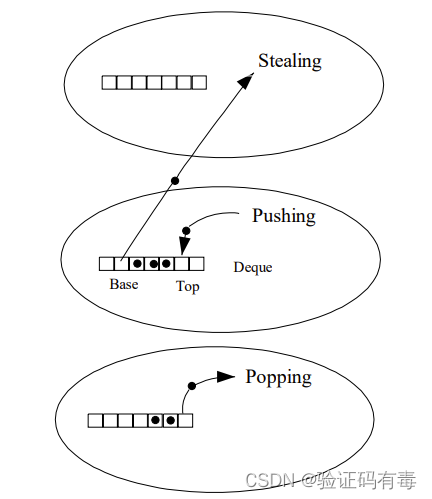
ForkJoinPool与ThreadPoolExecutor有个很大的不同之处在于，ForkJoinPool存在引入了工作窃取设计，它是其性能保证的关键之一。工作窃取，就是允许空闲线程从繁忙线程的双端队列中窃取任务。默认情况下，工作线程从它自己的双端队列的头部获取任务。但是，当自己的任务为空时，线程会从其他繁忙线程双端队列的尾部中获取任务。这种方法，最大限度地减少了线程竞争任务的可能性。

ForkJoinPool的大部分操作都发生在工作窃取队列（work-stealing queues ）中，该队列由内部类WorkQueue实现。它是Deques的特殊形式，但仅支持三种操作方式：push、pop和poll（也称为窃取）。在ForkJoinPool中，队列的读取有着严格的约束，push和pop仅能从其所属线程调用，而poll则可以从其他线程调用。
通过工作窃取，Fork/Join框架可以实现任务的自动负载均衡，以充分利用多核CPU的计算能力，同时也可以避免线程的饥饿和延迟问题
在这里插入图片描述

6.和普通线程池之间的区别

工作窃取算法
ForkJoinPool采用多任务队列，以及工作窃取算法来提高线程的利用率，而普通线程池则采用共享阻塞任务队列来管理任务。在工作窃取算法中，当一个线程完成自己的任务后，它可以从其它线程的队列中获取一个任务来执行，以此来提高线程的利用率。
任务的分解和合并
ForkJoinPool可以将一个大任务分解为多个小任务，并行地执行这些小任务，最终将它们的结果合并起来得到最终结果。而普通线程池只能按照提交的任务顺序一个一个地执行任务。
工作线程的数量
ForkJoinPool会根据当前系统的CPU核心数来自动设置工作线程的数量，以最大限度地发挥CPU的性能优势。而普通线程池需要手动设置线程池的大小，如果设置不合理，可能会导致线程过多或过少，从而影响程序的性能。
任务类型
ForkJoinPool适用于执行大规模任务并行化，而普通线程池适用于执行一些短小的任务，如处理请求等。

7.ForkJoinTask

ForkJoinTask是Fork/Join框架中的抽象类，它定义了执行任务的基本接口。用户可以通过继承ForkJoinTask类来实现自己的任务类，并重写其中的compute()方法来定义任务的执行逻辑。通常情况下我们不需要直接继承ForkJoinTask类，而只需要继承它的子类，Fork/Join框架提供了以下三个子类：