💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

文献来源：

 化石燃料短缺和环境保护在经济发展中引起了关注。大规模部署电动汽车(ev)可能是减少对化石燃料依赖和保护环境的潜在解决方案，许多国家和汽车制造商正在大力推广电动汽车的使用[1,2]。电动汽车在电力系统中往往以分布式和移动电源需求为代表;它们的分布式存储能力也适用于电网[3]。利用V2G (Vehicle to Grid)技术，电动汽车可以通过优化充放电来转移高峰负荷，降低发电机的运行成本和排放[4]。同时，大量电动汽车的不协调充放电也会导致电网出现电力拥塞、欠压、电网不稳定、电能质量、继电器、频率等电网问题[5-9]。

基于双层优化的大型电动汽车（EV）时空调度是一种综合考虑电动汽车充电需求、能源管理和出行需求的优化调度方法。这种方法通过将问题分解为两个层次的优化问题，来实现对大型电动汽车群体的有效调度。

下面是基于双层优化的大型电动汽车时空调度的一般步骤：

高层优化：
1. 问题定义：明确定义大型电动汽车时空调度的目标，例如最小化充电成本、最大化能源利用率等。同时，考虑到电动汽车的出行需求、能源管理策略等约束条件。

2. 空间调度：根据电动汽车出行需求和充电设施的分布，确定每个车辆的出行计划和路线。这包括考虑车辆之间的交通状况、充电设施的可用性等因素。

3. 时间调度：在空间调度的基础上，确定每个车辆的出发时间和到达时间，以满足出行需求，并尽可能优化充电计划。

低层优化：
1. 充电策略：针对每个电动汽车，基于车辆充电需求和能源管理策略，制定充电计划。这可能涉及到车辆的充电时间、功率、充电桩的选择等决策。

2. 能源管理：管理大量电动汽车充电过程中的能源需求与供给平衡。考虑到电网的负荷平衡、充电设施的容量限制，优化调度充电策略，使得车辆充电需求能够在可控范围内，并且尽可能减少成本。

3. 交互与协调：通过高层和低层优化过程的交互与协调，以实现整体调度的一致性和系统优化。

需要注意的是，基于双层优化的大型电动汽车时空调度是一个复杂的问题，涉及到多个因素的动态协调与优化。同时，还需要考虑到电动汽车充电设施的建设和管理，以及与电网的连接与交互等方面的问题。因此，综合运用优化方法、数据分析和智能算法等技术，能够有效地解决这一挑战并提供高效的调度方案。

📚2 运行结果

 

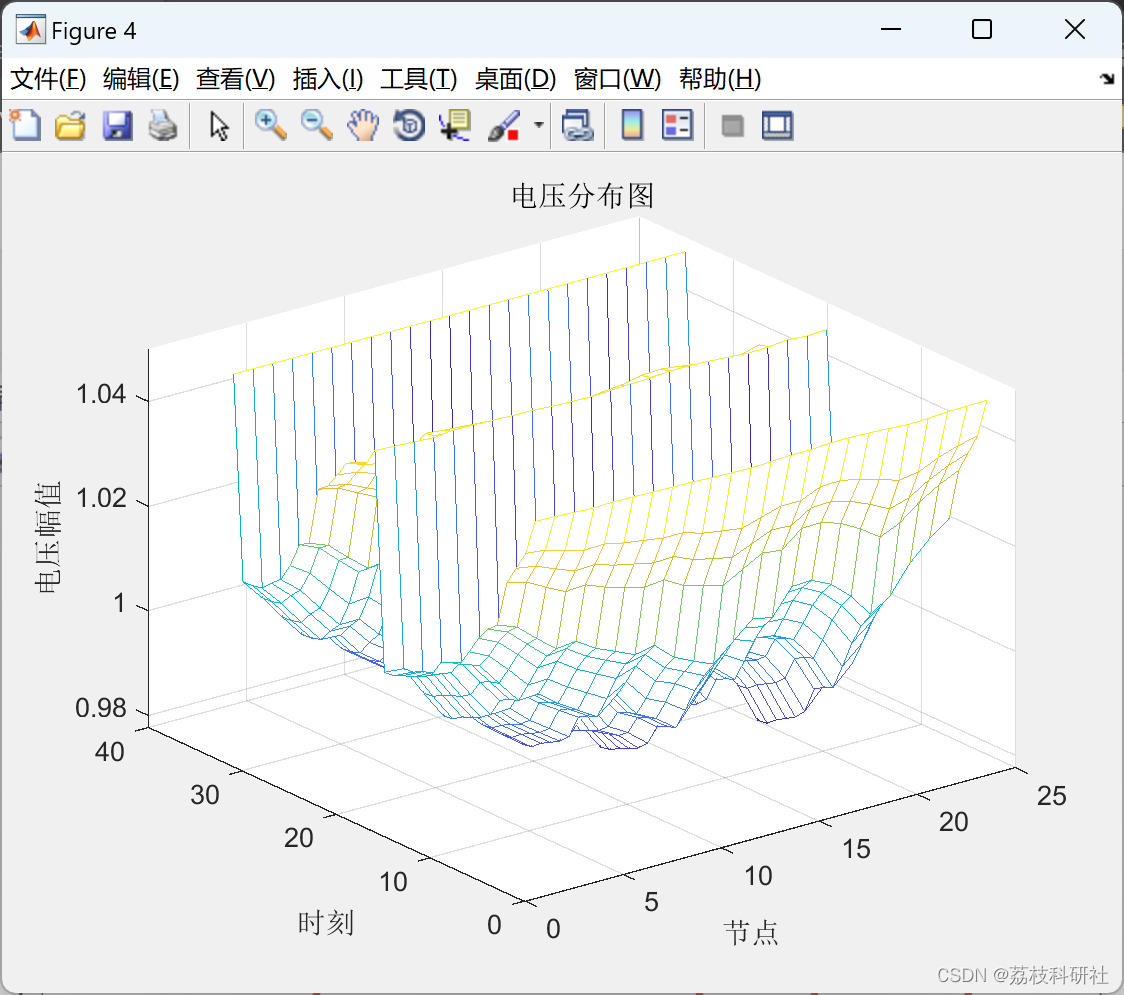
 数据：

部分代码：

Ndmax=15000*0.4*ones(24,20);%每时段最大接入放电电动汽车数量;150000辆电动车;
Ncmax=15000*0.95*ones(24,20);%每时段最大接入充电电动汽车数量;150000辆电动车;
%Ndmax=10000*0.4*ones(24,20);%每时段最大接入放电电动汽车数量;100000辆电动车;
%Ncmax=10000*0.95*ones(24,20);%每时段最大接入充电电动汽车数量;100000辆电动车;
%Ndmax=5000*0.4*ones(24,20);%每时段最大接入放电电动汽车数量;50000辆电动车;
%Ncmax=5000*0.95*ones(24,20);%每时段最大接入充电电动汽车数量;50000辆电动车;
%Ndmax=zeros(24,20);%输电网中不含电动汽车
%Ncmax=zeros(24,20);%输电网中不含电动汽车
Ndsummax=15000*3*ones(1,20);%全天电动汽车放电需求;150000辆电动车;
Ncsummax=15000*6*ones(1,20);%全天电动汽车充电需求;150000辆电动车;
%Ndsummax=10000*3*ones(1,20);%全天电动汽车放电需求;100000辆电动车;
%Ncsummax=10000*6*ones(1,20);%全天电动汽车充电需求;100000辆电动车;
%Ndsummax=5000*3*ones(1,20);%全天电动汽车放电需求;50000辆电动车;
%Ncsummax=5000*6*ones(1,20);%全天电动汽车充电需求;50000辆电动车;
%Ndsummax=zeros(1,20);%输电网中不含电动汽车
%Ncsummax=zeros(1,20);%输电网中不含电动汽车
priced=[0.06;0.06;0.07;0.08;0.09;0.1;0.12;0.15;0.2;0.25;0.3;0.35;0.25;0.2;0.15;0.1;0.09;0.1;0.15;0.25;0.2;0.1;0.08;0.07];%放电电价;放电电价高于充电电价的峰谷电价;
pricec=[0.06;0.06;0.07;0.08;0.09;0.1;0.11;0.12;0.14;0.16;0.17;0.18;0.16;0.14;0.12;0.095;0.09;0.1;0.12;0.16;0.14;0.1;0.08;0.07];%充电电价;放电电价高于充电电价的峰谷电价;
%priced=[0.06;0.06;0.07;0.08;0.09;0.1;0.11;0.12;0.14;0.16;0.17;0.18;0.16;0.14;0.12;0.095;0.09;0.1;0.12;0.16;0.14;0.1;0.08;0.07];%放电电价;峰谷电价;
%pricec=[0.06;0.06;0.07;0.08;0.09;0.1;0.11;0.12;0.14;0.16;0.17;0.18;0.16;0.14;0.12;0.095;0.09;0.1;0.12;0.16;0.14;0.1;0.08;0.07];%充电电价;峰谷电价;
%priced=0.08*ones(24,1);%放电电价:平电价;
%pricec=0.08*ones(24,1);%充电电价:平电价;
%%%%%MINLP转化为MILP求解%%%%%%%%%%%%%%%;
N=24;%线性化分段数;
X=binvar(Time,Ji);%0-1启停机变量;
S=sdpvar(Time,Ji);%机组启动费用;
PP=sdpvar(Time,Ji*N*SS);%线性化机组功率;
Pfx=sdpvar(Time,SS);%风机出力;
Nd=intvar(Time,SS);%电动汽车放电数量;
Nc=intvar(Time,SS);%电动汽车充电数量;
 

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

🌈4 Matlab代码实现