文章目录

Day43
- 最后一块石头的重量II
- - 题目
  - 思路
  - 代码
- 目标和
- - 题目
  - 思路
  - 代码
- 一和零
- - 题目
  - 思路
  - 代码

Day43

最后一块石头的重量II

1049. 最后一块石头的重量 II - 力扣（LeetCode）

题目

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；

如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

示例：

输入：[2,7,4,1,8,1]
输出：1

解释：

组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

提示：

1 <= stones.length <= 30
1 <= stones[i] <= 1000

思路

动规五部曲

确定dp数组（dp table）以及下标的含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。

可以回忆一下01背包中，dp[j]的含义，容量为j的背包，最多可以装的价值为 dp[j]。

相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”

确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题则是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

dp数组如何初始化

我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了。

当然也可以把石头遍历一遍，计算出石头总重量然后除2，得到dp数组的大小。

接下来就是如何初始化dp[j]呢，因为重量都不会是负数，所以dp[j]都初始化为0就可以了，这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);中dp[j]才不会初始值所覆盖。

确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中就已经说明：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

for (int i = 0; i < stones.size(); i++) { // 遍历物品
    for (int j = target; j >= stones[i]; j--) { // 遍历背包
        dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
    }
}

举例推导dp数组

举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dseWbVMI-1690548237342)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210121115805904.jpg “1049.最后一块石头的重量II”)]

最后dp[target]里是容量为target的背包所能背的最大重量。

代码

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int i = 0; i < stones.length; i++){
            sum += stones[i];
        }
        int target = sum / 2;
        int[] dp = new int[target + 1];
        dp[0] = 0;
        for(int i = 0; i < stones.length; i++){
            for(int j = target; j >= stones[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
            }
        }
        return sum - dp[target] - dp[target];
    }
}

目标和

494. 目标和 - 力扣（LeetCode）

题目

给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

输入：nums: [1, 1, 1, 1, 1], S: 3
输出：5

解释：

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

提示：

数组非空，且长度不会超过 20 。
初始的数组的和不会超过 1000 。
保证返回的最终结果能被 32 位整数存下。

思路

动态规划

如何转化为01背包问题呢。

假设加法的总和为x，那么减法对应的总和就是sum - x。

所以我们要求的是 x - (sum - x) = target

x = (target + sum) / 2

此时问题就转化为，装满容量为x的背包，有几种方法。

这里的x，就是bagSize，也就是我们后面要求的背包容量。

大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。

证明过程

代码随想录 (programmercarl.com)

动态规划五步曲

确定dp数组（dp table）以及下标的含义

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

其实也可以使用二维dp数组来求解本题，dp[i][j]：使用下标为[0, i]的nums[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种方法。

确定递推公式

有哪些来源可以推出dp[j]呢？

只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。

例如：dp[j]，j 为5，

已经有一个1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把所有的 dp[j - nums[i]] 累加起来。

所以求组合类问题的公式，都是类似这种：

dp[j] += dp[j - nums[i]]

dp数组如何初始化

从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲过对于01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。

举例推导dp数组

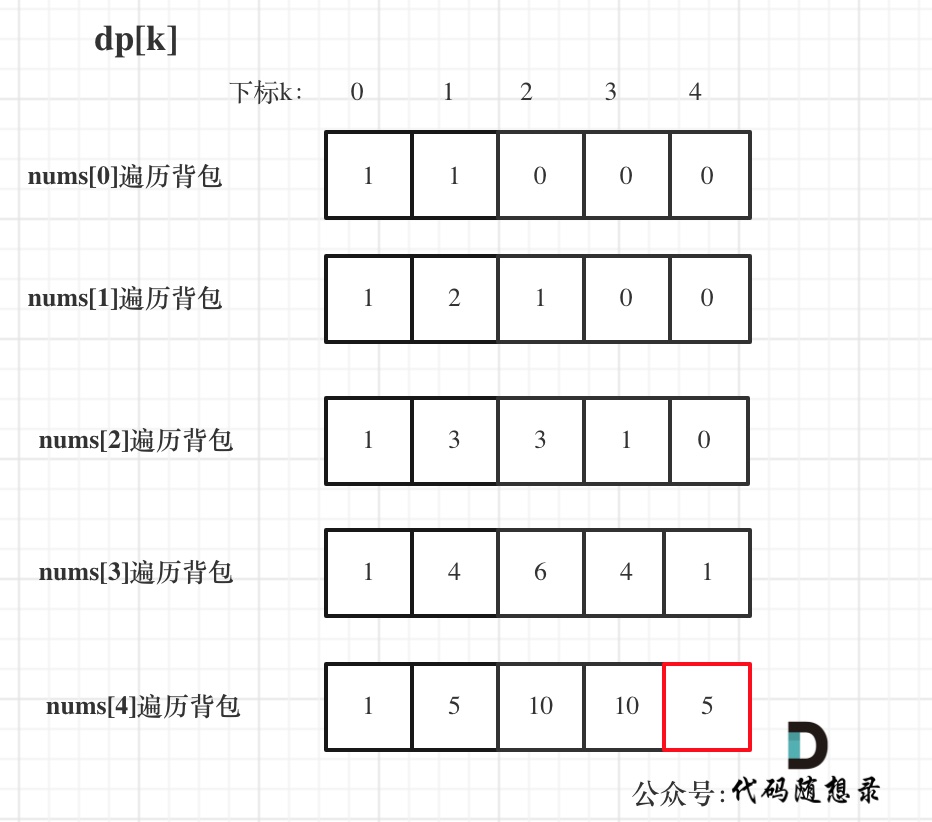
输入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

代码

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for(int i = 0; i < nums.length; i++){
            sum += nums[i];
        }
        //如果target过大 sum将无法满足
        if(sum < -target && target < 0) return 0;
        if((sum + target) % 2 != 0) return 0;
        int bagSize = (sum + target) / 2;

        int dp[] = new int[bagSize + 1];
        dp[0] = 1;
        for(int i = 0; i < nums.length; i++){
            for(int j = bagSize; j >= nums[i]; j--){
                dp[j] = dp[j - nums[i]] + dp[j];
            }
        }
        return dp[bagSize];
    }
}

一和零

474. 一和零 - 力扣（LeetCode）

题目

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

示例 1：

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

提示：

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100

思路

动规五部曲

确定dp数组（dp table）以及下标的含义

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

确定递推公式

dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取dp[i][j]的最大值。

所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。

dp数组如何初始化

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中已经讲解了，01背包的dp数组初始化为0就可以。

因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲到了01背包为什么一定是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。

			for(int i = m; i >= zeroNums; i--){
                for(int j = n; j >= oneNums; j--){
                    // 遍历背包容量且从后向前遍历！
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1);
                }
            }

那个遍历背包容量的两层for循环先后循序有没有什么讲究？

没讲究，都是物品重量的一个维度，先遍历哪个都行！

举例推导dp数组

以输入：[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3为例

最后dp数组的状态如下所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H64xq0NL-1690548237343)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210120111201512.jpg “474.一和零”)]

代码

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int dp[][] = new int[m + 1][n + 1];
        dp[0][0] = 0;
        for(String str : strs){ // 物品
            int zeroNums = 0, oneNums = 0;
            for(char c : str.toCharArray()){
                if (c == '0') zeroNums++;
                else oneNums++;
            }

            for(int i = m; i >= zeroNums; i--){
                for(int j = n; j >= oneNums; j--){
                    // 遍历背包容量且从后向前遍历！
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1);
                }
            }
        }
        return dp[m][n];
    }
}