文章目录
- 例题列表
- 291. 蒙德里安的梦想⭐⭐⭐⭐⭐
- 91. 最短Hamilton路径⭐⭐⭐
- 相关链接
例题列表
291. 蒙德里安的梦想⭐⭐⭐⭐⭐
https://www.acwing.com/problem/content/293/

当横向方格摆放完成后,纵向方格的拜访方式就已经确定了。(因为我们只要求横向方格的摆放方案。)
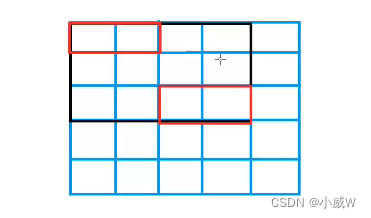
定义 DP 数组
dp[i][j] 表示 第 i 列中,有 j 集合的行伸出来了,即 i - 1 列的这一行放了横着的小方格。
例如这里有 5 行,j 的范围就是 0 ~ 1<<5 。
比较相邻的两列 j 和 k:
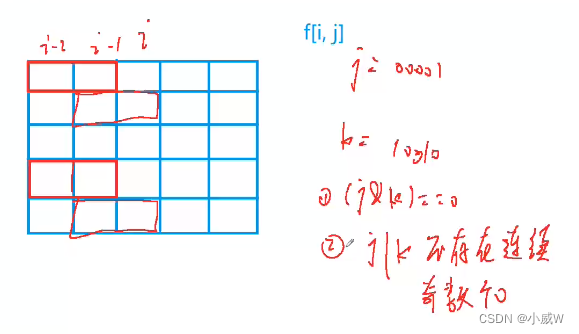
只要满足这两个条件就可以转移过来:
- (j & k) == 0 表示:没有冲突
- j | k 不存在连续的奇数个 0 表示:中间的间隔可以放下纵向的格子
注意这道题不能预先处理出所有的 st 数组,因为在 m 和 n 不一样时, st 数组中的值也会变得不一样。
dp 数组初始化:dp[0][0] = 1;
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
while (true) {
int n = sin.nextInt(), m = sin.nextInt();
if (n == 0 && m == 0) return;
op(n, m);
}
}
static void op(int n, int m) {
boolean[] st = new boolean[1 << n];
for (int i = 0; i < 1 << n; ++i) {
int cnt = 0;
st[i] = true;
for (int j = 0; j < n; ++j) {
if ((i >> j & 1) == 1) {
if ((cnt & 1) == 1) st[i] = false;
cnt = 0;
} else cnt++;
}
if ((cnt & 1) == 1) st[i] = false;
}
long[][] dp = new long[m + 1][1 << n];
dp[0][0] = 1;
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1<<n; ++j) {
for (int k = 0; k < 1<<n; ++k) {
if ((j & k) == 0 && st[j | k]) {
dp[i][j] += dp[i - 1][k];
}
}
}
}
System.out.println(dp[m][0]);
}
}
更多参考资料可见:
431 状态压缩DP 蒙德里安的梦想【动态规划】
Acwing291. 蒙德里安的梦想:状态压缩dp
91. 最短Hamilton路径⭐⭐⭐
https://www.acwing.com/activity/content/problem/content/1011/

先枚举集合,再枚举到达该集合的最后一个点,再枚举可以转移到该点该集合的状态。
dp 过程一共三重循环。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt();
int[][] d = new int[n][n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
d[i][j] = sin.nextInt();
}
}
// dp[i][j] 表示达到位置i,已经到达过的位置集合为j时的最短路径
long[][] dp = new long[n][1<<n];
for (int i = 0; i < n; ++i) Arrays.fill(dp[i], Long.MAX_VALUE / 2);
dp[0][1] = 0;
// 枚举每个可以到达的状态集合
for (int j = 0; j < 1 << n; ++j) {
// 枚举该集合可以到达的所有点
for (int i = 0; i < n; ++i) {
if ((j >> i & 1) == 1) { // 如果位置i是1
for (int k = 0; k < n; ++k) { // 从其它k=1但i位置=0的地方转移过来
if ((j >> k & 1) == 1) {
dp[i][j] = Math.min(dp[i][j], dp[k][j ^ (1 << i)] + d[k][i]);
}
}
}
}
}
System.out.println(dp[n - 1][(1 << n) - 1]);
}
}
注意:为什么要先枚举每个可以到达的状态集合 j,然后枚举该集合中可以到达的所有点 i,而不可以将枚举顺序反过来?
因为:
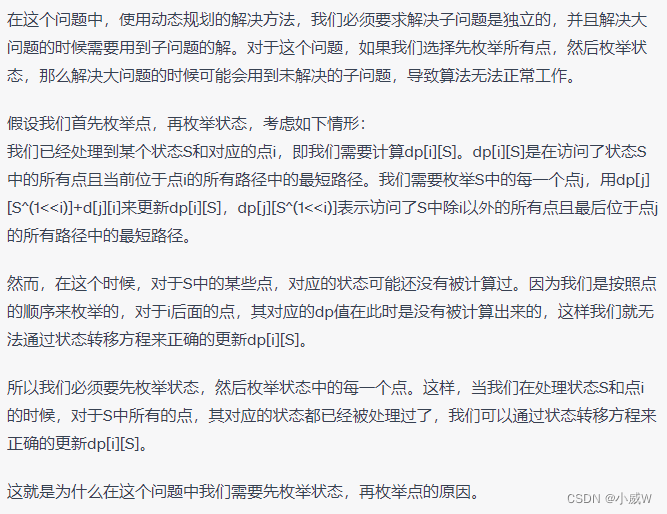
也就是先枚举点的话 不能保证前面的状态都被计算过。
相关链接
从集合论到位运算——常见位运算技巧及相关习题 & 状态压缩DP
【力扣周赛】第 355 场周赛(构造&二分答案&异或前缀 状态压缩⭐)








![BUU [BJDCTF2020]The mystery of ip](https://img-blog.csdnimg.cn/img_convert/981675958f66fe219d60e6b71fab53cd.jpeg)