一、137. 只出现一次的数字 II

1.题目简介

137. 只出现一次的数字 II
给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现三次。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且不使用额外空间来解决此问题。
在这里插入图片描述

2.解题思路

分别记录数组中所有元素每一个比特位的值出现的次数，其中将不能被3整除的比特位结合起来就是要找的值出现一次的数字

3.代码

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret = 0;
        for(int i = 0;i < 32; ++i)
        {
            int sum = 0;
            for(auto& e : nums)
            {
                if(((e >> i) & 1) == 1) sum++;
            }
            if(sum % 3)
            {
                ret |= (1 << i);
            }
        }
        return ret;
    }
};

4.运行结果

在这里插入图片描述

二、剑指 Offer 53 - II. 0～n-1中缺失的数字

1.题目简介

剑指 Offer 53 - II. 0～n-1中缺失的数字

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。
在这里插入图片描述

2.解题思路

二分法
寻找缺失的那个数，可能出现的情况有两种：
1.mid对应的数组元素nums[mid]等于mid此时我们应该在mid + 1~right之间寻找；
2.mid对应的数组元素不等于mid(只可能是比mid大，如果元素mid缺失nums[mid]就一定大于mid)此时我们应该在left~mid之间寻找。

当left == right时，会有两种情况：
1.left对应的元素nums[left]不等于left(大于left)，则缺失的数字就是left(缺失的数字在0~n-2之间)
2.left对应的元素nums[left]等于left，则缺失的数字就是left+1(缺失的数字是n-1)

3.代码

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] == mid) left = mid + 1;
            else right = mid;
        }
        return left == nums[left] ? left + 1 : left;
    }
};

4.运行结果

在这里插入图片描述

三、153. 寻找旋转排序数组中的最小值

1.题目简介

153. 寻找旋转排序数组中的最小值
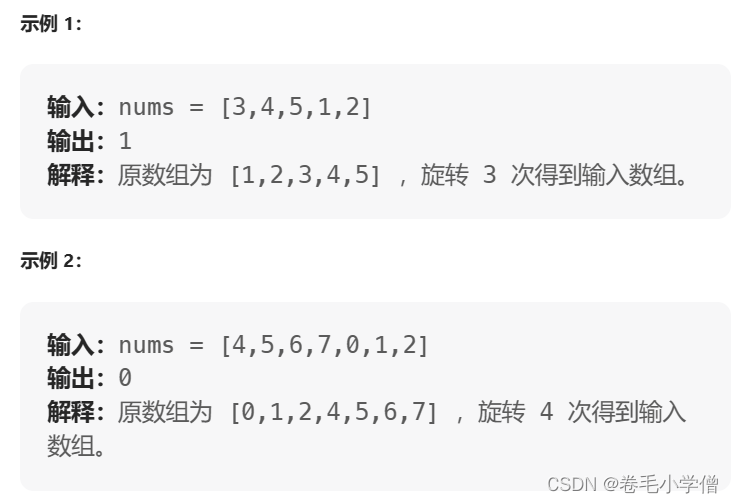
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值互不相同的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
在这里插入图片描述

2.解题思路

二分法
将数组分为两部分升序的子数组：A_B和CD两部分(A是第一部分的第一个元素，B是第一部分的最后一个元素；C和D类似)

3.代码

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] > nums[right]) //说明mid位于第一部分。则要在mid + 1~right之间寻找数组的最小值
            left = mid + 1;
            else//说明mid位于第二部分，则要在left~mid之间进行寻找
            right = mid;
        }
        return nums[left];
    }
};