【小白从小学Python、C、Java】

【计算机等考+500强证书+考研】

【Python-数据分析】

沿指定轴方向

计算标准(偏)差

numpy.nanstd()

[太阳]选择题

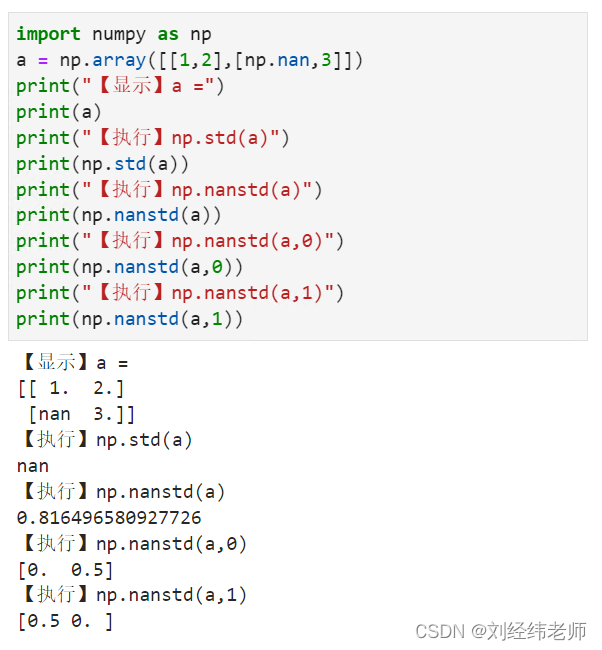
import numpy as np

a = np.array([[1,2],[np.nan,3]])

print("【显示】a =")

print(a)

print("【执行】np.std(a)")

print(np.std(a))

print("【执行】np.nanstd(a)")

print(np.nanstd(a))

print("【执行】np.nanstd(a,0)")

print(np.nanstd(a,0))

print("【执行】np.nanstd(a,1)")

print(np.nanstd(a,1))

以下说法错误的是：

A选项：np.std(a)结果为nan

B选项：np.nanstd(a)结果为[0. 0.5]

C选项：np.nanstd(a,0)结果为[0. 0.5]

D选项：np.nanstd(a,1)结果为[0.5 0.]

[太阳]温馨期待

期待大家提出宝贵建议，互相交流，收获更大，助教：hq

正确答案是：B

图1 问题解析

图2 题目运行代码

欢迎大家转发，一起传播知识和正能量，帮助到更多人。期待大家提出宝贵改进建议，互相交流，收获更大。辛苦大家转发时注明出处(也是咱们公益编程交流群的入口网址)，刘经纬老师共享知识相关文件下载地址为：https://liujingwei.cn