实验12 动态查找2022

news2024/11/19 7:46:48

A. DS二叉排序树之创建和插入

给出一个数据序列，建立二叉排序树，并实现插入功能

对二叉排序树进行中序遍历，可以得到有序的数据序列

输入

第一行输入t，表示有t个数据序列

第二行输入n，表示首个序列包含n个数据

第三行输入n个数据，都是自然数且互不相同，数据之间用空格隔开

第四行输入m，表示要插入m个数据

从第五行起，输入m行，每行一个要插入的数据，都是自然数且和前面的数据不等

以此类推输入下一个示例

1
6
22 33 55 66 11 44
3
77
50
10

输出

第一行输出有序的数据序列，对二叉排序树进行中序遍历可以得到

从第二行起，输出插入第m个数据后的有序序列，输出m行

以此类推输出下一个示例的结果

11 22 33 44 55 66 
11 22 33 44 55 66 77 
11 22 33 44 50 55 66 77 
10 11 22 33 44 50 55 66 77 
#include<iostream>
using namespace std;
struct node {
	int data;
	node* lchild;
	node* rchild;
};
void inorder(node *root) {
	if (root->lchild != NULL) inorder(root->lchild);
	cout << root->data << " ";
	if (root->rchild != NULL) inorder(root->rchild);
}
void insert(node* root, node* s) {
	if (s->data < root->data) {
		if (root->lchild != NULL) insert(root->lchild, s);
		else {
			root->lchild = s; return;
		}
	}
	else {
		if (root->rchild != NULL) insert(root->rchild, s);
		else {
			root->rchild = s; return;
		}
	}
}
int main() {
	int t; cin >> t;
	while (t--) {
		int num; cin >> num;
		int sum; cin >> sum;
		node* root=new node{sum,NULL,NULL};
		for (int i = 0; i < num - 1; i++) {
			cin >> sum;
			node* s = new node{ sum,NULL,NULL };
			insert(root, s);
		}
		inorder(root); cout << endl;
		cin >> num;
		while (num--) {
			cin >> sum;
			node* s = new node{ sum,NULL,NULL };
			insert(root, s);
			inorder(root); cout << endl;
		}
	}
}

B. DS二叉排序树之查找

给出一个数据序列，建立二叉排序树，并实现查找功能

对二叉排序树进行中序遍历，可以得到有序的数据序列

输入

第一行输入t，表示有t个数据序列

第二行输入n，表示首个序列包含n个数据

第三行输入n个数据，都是自然数且互不相同，数据之间用空格隔开

第四行输入m，表示要查找m个数据

从第五行起，输入m行，每行一个要查找的数据，都是自然数

以此类推输入下一个示例

1
6
22 33 55 66 11 44
7
11
22
33
44
55
66
77

输出

第一行输出有序的数据序列，对二叉排序树进行中序遍历可以得到

从第二行起，输出查找结果，如果查找成功输出查找次数，如果查找失败输出-1

以此类推输出下一个示例的结果

11 22 33 44 55 66 
2
1
2
4
3
4
-1
#include<iostream>
using namespace std;
struct node {
	int data;
	node* lchild;
	node* rchild;
};
class Tree {
public:
	node* root;
	int count=0;
	Tree();
	void inorder(node* root);
	void insert(node* root, node* s);
	void research(node* root, int num);
};
Tree::Tree() {
	root = new node{0,NULL,NULL};
}
void Tree::inorder(node* root) {
	if (root->lchild != NULL) inorder(root->lchild);
	cout << root->data << " ";
	if (root->rchild != NULL) inorder(root->rchild);
}
void Tree::insert(node* root, node* s) {
	if (s->data < root->data) {
		if (root->lchild != NULL) insert(root->lchild, s);
		else {
			root->lchild = s; return;
		}
	}
	else {
		if (root->rchild != NULL) insert(root->rchild, s);
		else {
			root->rchild = s; return;
		}
	}
}
void Tree::research(node *root,int num) {
	count++;
	node* next = new node;
	if (root->data == num) return;
	else {
		if (root->data > num) next = root->lchild;
		else next = root->rchild;
	}
	if (next) research(next, num);
	else count = 0;
}
int main() {
	int t; cin >> t;
	while (t--) {
		int sum,num;
		cin >> sum >> num;
		Tree* tree = new Tree;
		tree->root->data = num;
		for (int i = 0; i < sum - 1; i++) {
			cin >> num;
			node* s = new node{ num,NULL,NULL };
			tree->insert(tree->root, s);
		}
		tree->inorder(tree->root); cout << endl;
		cin >> sum;
		while (sum--) {
			tree->count = 0;
			cin >> num;
			tree->research(tree->root, num);
			if (tree->count != 0) cout << tree->count << endl;
			else cout << "-1" << endl;
		}
	}
}

C. DS二叉排序树之删除

给出一个数据序列，建立二叉排序树，并实现删除功能

对二叉排序树进行中序遍历，可以得到有序的数据序列

输入

第一行输入t，表示有t个数据序列

第二行输入n，表示首个序列包含n个数据

第三行输入n个数据，都是自然数且互不相同，数据之间用空格隔开

第四行输入m，表示要删除m个数据

从第五行起，输入m行，每行一个要删除的数据，都是自然数

以此类推输入下一个示例

1
6
22 33 55 66 11 44
3
66
22
77

输出

第一行输出有序的数据序列，对二叉排序树进行中序遍历可以得到

从第二行起，输出删除第m个数据后的有序序列，输出m行

以此类推输出下一个示例的结果

11 22 33 44 55 66 
11 22 33 44 55 
11 33 44 55 
11 33 44 55

提示

当删除数据不在序列中，那么删除操作等于不执行，所以输出序列不变化

#include<iostream>
using namespace std;
struct node {
	int data;
	node* lchild;
	node* rchild;
};
class Tree {
public:
	node* root;
	node* temp;
	node* pre;
	int flag=0;
	int count = 0;
	Tree();
	void inorder(node* root);
	void insert(node* root, node* s);
	node* search(node* root, int num);
	void remove(node* root, int num);
	int check(node* p, int num);
};
int Tree::check(node* root, int num) {
	if (num > root->data)
	{
		if (root->rchild == NULL) { flag = 1; return -1; }
		if (root->rchild->data == num)
		{
			if (root->rchild->lchild == NULL && root->rchild->rchild == NULL)pre = root;
		}
		check(root->rchild, num);
	}
	else if (num == root->data)
	{
		temp = root;
		return 1;
	}
	else if (num < root->data)
	{
		if (root->lchild == NULL) { flag = 1; return -1;}
		if (root->lchild->data == num)
		{
			if (root->lchild->lchild == NULL && root->lchild->rchild == NULL)pre = root;
		}
		check(root->lchild, num);
	}
	if (flag == 1) return -1;
	else return 1;
}
void Tree::remove(node* p, int num) {
	if (!p->rchild && p->lchild != NULL) {
		node* q = new node();
		q = p;
		p = p->lchild;
		delete p;
	}
	else if (!p->lchild && p->rchild != NULL)
	{
		node* q = new node();
		q = p;
		p = p->lchild;
		delete q;
	}
	else if (p->lchild == NULL && p->rchild == NULL) {
		if (pre->lchild->data == num) pre->lchild = NULL;
		else pre->rchild = NULL;
		node* q = new node();
		q = p;
		delete q;
	}
	else {
		node* q = new node();
		node* s = new node();
		q = p;
		s = p->lchild;
		while (s->rchild) {
			q = s;
			s = s->rchild;
		}
		p->data = s->data;
		if (q != p) q->rchild = s->lchild;
		else q->lchild = s->lchild;
		delete s;
	}
}
Tree::Tree() {
	root = new node{ -1,NULL,NULL };
}
void Tree::inorder(node* root) {
	if (root->lchild) inorder(root->lchild);
	cout << root->data << " ";
	if (root->rchild) inorder(root->rchild);
}
void Tree::insert(node* root, node* s) {
	if (s->data < root->data) {
		if (root->lchild != NULL) insert(root->lchild, s);
		else {
			root->lchild = s; return;
		}
	}
	else {
		if (root->rchild != NULL) insert(root->rchild, s);
		else {
			root->rchild = s; return;
		}
	}
}
node* Tree::search(node* root, int num) {
	if (root == NULL) return NULL;
	count++;
	node* next = new node;
	if (root->data == num) return root;
	else {
		if (root->data > num) next = root->lchild;
		else next = root->rchild;
	}
	if (next) return search(next, num);
	else {
		count = 0; return NULL;
	}
}
int main() {
	int t; cin >> t;
	while (t--) {
		int sum, num;
		cin >> sum >> num;
		Tree* tree = new Tree;
		tree->root->data = num;
		for (int i = 0; i < sum - 1; i++) {
			cin >> num;
			node* s = new node{ num,NULL,NULL };
			tree->insert(tree->root, s);
		}
		tree->inorder(tree->root); cout << endl;
		cin >> sum;
		while (sum--) {
			cin >> num;
			int flag = tree->check(tree->root, num);
			if(flag==1)tree->remove(tree->temp, num);
			tree->inorder(tree->root); cout << endl;
		}
	}
}

D. DS查找—二叉树平衡因子

二叉树用数组存储，将二叉树的结点数据依次自上而下,自左至右存储到数组中，一般二叉树与完全二叉树对比，比完全二叉树缺少的结点在数组中用0来表示。

计算二叉树每个结点的平衡因子，并按后序遍历的顺序输出结点的平衡因子。

--程序要求--

若使用C++只能include一个头文件iostream；若使用C语言只能include一个头文件stdio

程序中若include多过一个头文件，不看代码，作0分处理

不允许使用第三方对象或函数实现本题的要求

输入

测试次数t

每组测试数据一行，数组元素个数n，后跟n个字符，二叉树的数组存储。

2
6 ABC00D
24 ABCD0EF0000H00000000000I

输出

对每组测试数据，按后序遍历的顺序输出树中结点的平衡因子（测试数据没有空树）

B 0
D 0
C 1
A -1
D 0
B 1
I 0
H 1
E 2
F 0
C 2
A -2

#include<iostream>
using namespace std;
int height(char* tree, int i, int n) {
	if (tree[i] == '0' || i >= n) return 0;
	else {
		int left = height(tree, 2 * i + 1, n) + 1;
		int right = height(tree, 2 * i + 2, n) + 1;
		return left > right ? left : right;
	}
}
void func(char* tree, int i, int n) {
	if (i < n) {
		if (tree[i] != '0') {
			func(tree, 2*i+1,n);
			func(tree, 2 * i + 2, n);
			int differrnt = height(tree, 2 * i + 1, n) - height(tree, 2 * i + 2, n);
			cout << tree[i] << " " << differrnt << endl;
		}
	}
}
int main() {
	int t; cin >> t;
	while (t--) {
		int n; cin >> n;
		char* tree = new char[n + 1];
		for (int i = 0; i < n; i++) cin >> tree[i];
		func(tree, 0, n);
	}
}

E. DS哈希查找—二次探测再散列

定义哈希函数为H(key) = key%11。输入表长（大于、等于11），输入关键字集合，用二次探测再散列构建哈希表，并查找给定关键字。

输入

测试次数t

每组测试数据格式如下：

哈希表长m、关键字个数n

n个关键字

查找次数k

k个待查关键字

1
12 10
22 19 21 8 9 30 33 4 41 13
4
22
15
30
41

输出

对每组测试数据，输出以下信息：

构造的哈希表信息，数组中没有关键字的位置输出NULL

对k个待查关键字，分别输出：

0或1（0—不成功，1—成功）、比较次数、查找成功的位置（从1开始）

22 9 13 NULL 4 41 NULL 30 19 8 21 33
1 1 1
0 3
1 3 8
1 6 6

#include<iostream>
using namespace std;
int main() {
	int t; cin >> t;
	while (t--) {
		int m, n;
		cin >> m >> n;
		int* a = new int[m + 1];
		for (int i = 0; i < m + 1; i++)a[i] = -9999;
		for (int i = 0; i < n; i++) {
			int num; cin >> num;
			int power = 0,flag=0;
			while (power <= m / 2) {
				flag++;
				int sign;
				if (flag >= 2 && flag % 2 == 0) power++;
				if (flag % 2 == 0) sign = 1;
				else sign = -1;
				int index = (num % 11 + sign * power * power) % m;
				if (index < 0) index = m + index;
				if (a[index] == -9999) {
					a[index] = num; break;
				}
			}
		}
		for (int i = 0; i < m; i++) {
			if (a[i] != -9999) cout << a[i];
			else cout << "NULL";
			if (i != m - 1) cout << " ";
			else cout << endl;
		}
		int tt; cin >> tt;
		while (tt--) {
			int num; cin >> num;
			int time = 0, power = 0, flag = 0;
			while (1) {
				time++; flag++;
				int sign;
				if (flag >= 2 && flag % 2 == 0) power++;
				if (flag % 2 == 0) sign = 1;
				else sign = -1;
				int index = (num % 11 + sign * power * power) % m;
				if (index < 0) index = m + index;
				if (a[index] == -9999 || power > m / 2) {
					cout << "0 " << time << endl;
					break;
				}
				if (a[index] == num) {
					cout << "1 " << time << " " << index + 1 << endl;
					break;
				}
			}
		}
	}
	return 0;
}

F. DS哈希查找--链地址法(表头插入)

给出一个数据序列，建立哈希表，采用求余法作为哈希函数，模数为11，哈希冲突用链地址法和表头插入

如果首次查找失败，就把数据插入到相应的位置中

实现哈希查找功能

输入

第一行输入n，表示有n个数据
第二行输入n个数据，都是自然数且互不相同，数据之间用空格隔开
第三行输入t，表示要查找t个数据
从第四行起，每行输入一个要查找的数据，都是正整数

6
11 23 39 48 75 62
6
39
52
52
63
63
52

输出

每行输出对应数据的查找结果

6 1
error
8 1
error
8 1
8 2

注意，当两次输入要相同的查找数据，如果第一次查找不成功就会执行插入，那么第二次查找必然成功，且查找次数为1次（因为做表头插入）

例如示例数据中输入两次52，第一次查找失败就把52插入到位置8，第二次查找就成功了，所以第一次输出error，第二次就输出8 1

为什么第三次输入52会输出8 2

#include<iostream>
using namespace std;
struct node {
	int data;
	int key;
	struct node* next;
};
class Hash {
public:
	node* hash;
	int n;
	Hash(int n);
	void insert(int index, int num);
	void search(int num);
};
Hash::Hash(int n) {
	this->n = n;
	hash = new node[20];
}
void Hash::insert(int index, int num) {
	node* p = new node();
	p->next = hash[index].next;
	p->data = hash[index].data;
	hash[index].data = num;
	hash[index].next = p;
}
void Hash::search(int num) {
	int num1 = num % 11, count = 0,flag=0;
	node* p = new node();
	for (int i = 0; i < n; i++) {
		if (hash[i].key == num1) {
			flag = 1;
			p = &hash[i];
			while (p != NULL) {
				count++;
				if (p->data == num) {
					cout << num1 << " " << count << endl;
					break;
				}
				p = p->next;
			}
			if (p == NULL) {
				cout << "error" << endl;
				insert(i, num);
			}
			break;
		}
	}
	if (flag == 0) {
		cout << "error" << endl;
		n += 1;
		hash[n - 1].data = num;
		hash[n - 1].key = num % 11;
		hash[n - 1].next = NULL;
	}
}
int main() {
	int n,num; cin >> n;
	Hash hs(n);
	for (int i = 0; i < n; i++) {
		cin >> num;
		hs.hash[i].key = num % 11;
		hs.hash[i].data = num;
		hs.hash[i].next = NULL;
	}
	int t; cin >> t;
	while (t--) {
		cin >> num;
		hs.search(num);
	}
	return 0;
}

G. DS哈希查找--Trie树

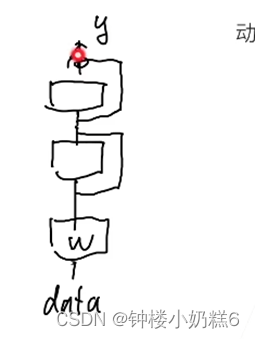
Trie树又称单词查找树，是一种树形结构，如下图所示。

 

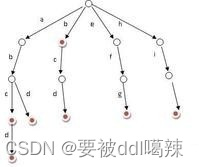
它是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来节约存储空间，最大限度地减少无谓的字符串比较，查询效率比哈希表高。

输入的一组单词，创建Trie树。输入字符串，计算以该字符串为公共前缀的单词数。

（提示：树结点有26个指针，指向单词的下一字母结点。）

输入

测试数据有多组

每组测试数据格式为：

第一行：一行单词，单词全小写字母，且单词不会重复，单词的长度不超过10

第二行：测试公共前缀字符串数量t

后跟t行，每行一个字符串

abcd abd bcd efg hig
3
ab
bc
abcde

输出

每组测试数据输出格式为：

第一行：创建的Trie树的层次遍历结果

第2~t+1行：对每行字符串，输出树中以该字符串为公共前缀的单词数。

abehbcficddggd
2
1
0
#include<iostream>
#include<string>
#include<iostream>
#include<queue>
using namespace std;
struct node {
	char data;
	struct node* next[26];
};
class Trie {
public:
	struct node* trie;
	Trie();
	int getnum(node* t);
	void print(node *t);
};
Trie::Trie() {
	trie = new node[26];
	for (int i = 0; i < 26; i++) {
		trie[i].data = '0';
		for (int j = 0; j < 26; j++) trie[i].next[j] = NULL;
	}
}
void Trie::print(node* t) {
	queue<node*> q;
	for (int i = 0; i < 26; i++) {
		if (t[i].data != '0') q.push(&t[i]);
	}
	while (!q.empty()) {
		node* p = q.front();
		q.pop();
		cout << p->data;
		for (int i = 0; i < 26; i++) {
			if (p->next[i] != NULL) q.push(p->next[i]);
		}
	}
	cout << endl;
}
int Trie::getnum(node* t) {
	int count = 0;
	for (int i = 0; i < 26; i++) {
		if (t->next[i] != NULL) count += getnum(t->next[i]);
	}
	if (count == 0) return 1;
	else return count;
}
int main() {
	char* s = new char[10000];
	int n = 0;
	while ((s[n] = getchar()) != '\n') n++;
	Trie ti;
	for (int i = 0; i < n; i++) {
		string s1;
		while (s[i] != ' ' && i < n) {
			s1 += s[i]; i++;
		}
		node* fa = &ti.trie[s1[0] - 'a'];
		fa->data = s1[0];
		for (int j = 1; j < (int)s1.length(); j++) {
			if (fa->next[s1[j] - 'a'] != NULL) {
				fa = fa->next[s1[j] - 'a'];
				continue;
			}
			node* temp = new node;
			temp->data = s1[j];
			for (int k = 0; k < 26; k++) temp->next[k] = NULL;
			fa->next[s1[j] - 'a'] = temp;
			fa = fa->next[s1[j] - 'a'];
		}
	}
	ti.print(ti.trie); 
	int t; cin >>t;
	string ss;
	for (int i = 0; i < t; i++) {
		cin >> ss;
		node* fa = &ti.trie[ss[0] - 'a'];
		for (int j = 1; j < (int)ss.length(); j++) {
			fa = fa->next[ss[j] - 'a'];
			if (fa == NULL) break;
		}
		if (fa == NULL) cout << "0" << endl;
		else cout << ti.getnum(fa)<<endl;
	}
	return 0;
}

H. 搜索树判断

对于二叉搜索树，我们规定任一结点的左子树仅包含严格小于该结点的键值，而其右子树包含大于或等于该结点的键值。如果我们交换每个节点的左子树和右子树，得到的树叫做镜像二叉搜索树。

现在我们给出一个整数键值序列，请编写程序判断该序列是否为某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列，如果是，则输出对应二叉树的后序遍历序列。

输入

输入的第一行包含一个正整数N（≤1000），第二行包含N个整数，为给出的整数键值序列，数字间以空格分隔。

7
8 6 5 7 10 8 11

输出

输出的第一行首先给出判断结果，如果输入的序列是某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列，则输出YES，否侧输出NO。如果判断结果是YES，下一行输出对应二叉树的后序遍历序列。数字间以空格分隔，但行尾不能有多余的空格。

YES
5 7 6 8 11 10 8
#include<iostream>
using namespace std;
struct node {
	int data;
	node* lchild;
	node* rchild;
};
class Tree {
	node* root;
	int* pre;
	int* post;
	int* a;
	int n;
public:
	Tree(int n);
	void create(int *a);
	void insert(node* root, node *s);
	void postorder(node*root,int& count);
	void preorder(node* root,int& count);
	bool pre_dst();
	bool post_dst();
	void print();
};
void Tree::print() {
	int count1 = 0, count2 = 0;
	preorder(root, count1);
	postorder(root, count2);
	if (pre_dst() || post_dst()) {
		cout << "YES" << endl;
		for (int i = 0; i < n - 1; i++) cout << post[i] << " ";
		cout << post[n - 1];
	}
	else cout << "NO" << endl;
}

bool Tree::pre_dst() {//初始序列与先序序列或者初始序列的倒序与后序序列是否相等
	bool flag=true;
	for (int i = 0; i < n; i++) 
		if (a[i] != pre[i]) {
			flag = false;
			break;
		}
	return flag;
}
bool Tree::post_dst() {
	bool flag = true;
	for (int i = 0; i < n; i++)
		if (a[i] != post[n - i + 1]) {
			flag = false;
			break;
		}
	return flag;
}
void Tree::preorder(node* root,int& count) {
	if (root == NULL) return;
	pre[count++] = root->data;
	preorder(root->lchild,count);
	preorder(root->rchild, count);
}
void Tree::postorder(node* root, int& count) {
	if (root == NULL) return;
	postorder(root->lchild, count);
	postorder(root->rchild, count);
	post[count++] = root->data;
}
Tree::Tree(int n) {
	this->n = n;
	a = new int[n];
	pre = new int[n];
	post = new int[n];
}
void Tree::insert(node* root, node* s) {
	if (s->data < root->data) {
		if (root->lchild != NULL) insert(root->lchild, s);
		else {
			root->lchild = s; return;
		}
	}
	else {
		if (root->rchild != NULL) insert(root->rchild, s);
		else {
			root->rchild = s; return;
		}
	}
}
void Tree::create(int *a) {
	for (int i = 0; i < n; i++) this->a[i]= a[i];
	root = new node{ a[0],NULL,NULL };
	for (int i = 1; i < n; i++) {
		node* s = new node{ a[i],NULL,NULL};
		insert(root,s);
	}
}
int main() {
	int n; cin >> n;
	int* a = new int[n];
	for (int i = 0; i < n; i++) cin >> a[i];
	Tree *tree=new Tree(n);
	tree->create(a);
	tree->print();
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/80968.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Vue 基础详解 | 系统性学习 | 无知的我费曼笔记

Vue 基础详解 | 系统性学习 | 无知的我费曼笔记

无知的我正在复盘Vue 该笔记特点是 重新整理了涉及资料的一些语言描述、排版而使用了自己的描述对一些地方做了补充说明。比如解释专有名词、类比说明、对比说明、注意事项提升了总结归纳性。尽可能在每个知识点上都使用一句话 || 关键词概括更注重在实际上怎么应用提出并回答…
阅读更多...
spring——AOP面向切面编程—— 自动代理——根据 Bean 名称创建代理对象根据切面中信息创建代理对象...

spring——AOP面向切面编程—— 自动代理——根据 Bean 名称创建代理对象根据切面中信息创建代理对象...

自动代理 在前面的案例中&#xff0c;所有目标对象(Target Bean)的代理对象(Proxy Bean)都是在 XML 配置中通过 ProxyFactoryBean 创建的。 但在实际开发中&#xff0c;一个项目中往往包含非常多的 Bean&#xff0c; 如果每个 Bean 都通过 ProxyFactoryBean 创建&#xff0c;那…
阅读更多...
MySQL~InnoDB关键特性(插入缓存、俩次写、自适应哈希索引、异步IO

MySQL~InnoDB关键特性(插入缓存、俩次写、自适应哈希索引、异步IO

一般情况下&#xff0c;主键是行唯一的标识符。通常应用程序中行记录的插入顺序是按照主键递增的顺序进行插入的。因此&#xff0c;插入聚集索引一般是顺序的&#xff0c;不需要磁盘的随机读取。因为&#xff0c;对于此类情况下的插入&#xff0c;速度还是非常快的。 如果索引…
阅读更多...
Selenium4+Python3系列 - 测试框架的设计与开发

Selenium4+Python3系列 - 测试框架的设计与开发

框架搭建 整个框架的实现&#xff0c;大约也就1.5天&#xff0c;关于框架的开发并不是很难&#xff0c;主要难在测试报告增加失败自动截图功能和echart的饼子图统计功能&#xff0c;两者的整合花了近半天的时间吧。 效果&#xff1a; 1、核心思想 延续使用Page Object和Page …
阅读更多...
RabbitMQ入门（三）消息应答与发布确认

RabbitMQ入门（三）消息应答与发布确认

前言&#xff1a; 消息应答与发布确认都是保证消息不丢失。而重复消费问题则是消息幂等性。&#xff08;之后会说幂等性&#xff09; 消息应答&#xff1a; 应答功能属于消费者&#xff0c;消费者在接收到消息并且处理该消息之后&#xff0c;告诉 rabbitmq 它已经处理了&…
阅读更多...
深度学习——残差网络(ResNet)笔记

深度学习——残差网络(ResNet)笔记

残差网络&#xff1a;经常使用的网络之一 1.随着神经网络的不断加深能改进精度吗&#xff1f; 不一定 ①蓝色五角星表示最优值&#xff0c;Fi闭合区域表示函数&#xff0c;闭合区域的面积代表函数的复杂程度。在这个区域能够找到一个最优的模型&#xff08;区域中的一个点表…
阅读更多...
「重学JS」带你一文吃透作用域与闭包

「重学JS」带你一文吃透作用域与闭包

前言 学习了这么久前端&#xff0c;发现自己对于基础知识的掌握并没有那么通透&#xff0c;于是打算重新学一遍JS&#xff0c;借用经济学的一句话&#xff1a;JS基础决定能力高度&#x1f926;&#x1f3fb; 基础很重要&#xff0c;只有基础好才会很少出 bug&#xff0c;大多数…
阅读更多...
二叉树的性质

二叉树的性质

由于二叉树的结构特殊&#xff0c;会有一系列的数学性质 性质一&#xff1a;对于一棵二叉树&#xff0c;第i层的最大结点数量为 个&#xff0c;比如二叉树的第一层只有一个根结点&#xff0c;而二叉树的第三层可以有 个结点。 性质二&#xff1a;对于一棵深度为k的二叉树&am…
阅读更多...
【Python】函数

【Python】函数

文章目录1. 函数介绍2. 函数的定义与调用3. 函数参数4. 函数返回值5. 变量作用域6. 函数执行过程7. 链式调用8. 嵌套调用9. 函数递归10. 参数默认值11关键字参数1. 函数介绍 编程中的函数不同于数学中的函数&#xff1a; 数学上的函数&#xff0c;比如 y sin x&#xff0c;x…
阅读更多...
Vue快速上门|了解MVVM

Vue快速上门|了解MVVM

1.1、先了解下MVVM VUE是基于MVVM思想实现的，❓那什么是MVVM呢？—— MVVM，是Model-View-ViewModel的缩写，是一种软件架构模式。其核心思想就是分离视图、数据、逻辑，VUE框架解决了数据Model到视图View的双向绑定，我们只关注业务逻辑ViewModel即可，极大的提高的编程效率…
阅读更多...
BadUSB超详细制作, 实现CobaltStrike远控上线

BadUSB超详细制作, 实现CobaltStrike远控上线

前言 在2014年美国黑帽大会上&#xff0c;安全研究人员JakobLell和独立安全研究人员Karsten Nohl展示了他们称为“BadUSB”的攻击方法&#xff0c;这种攻击方法让USB安全和几乎所有和USB相关的设备(包括具有USB端口的电脑)都陷入相当危险的状态 现在的USB设备很多&#xff0c…
阅读更多...
高级篇之ENC1当作采集卡使用方案推荐

高级篇之ENC1当作采集卡使用方案推荐

高级篇之ENC1当作采集卡使用0 背景&#xff1a;1 准备工作2 连接示意图3 配置步骤&#xff1a;3.1 在笔记本电脑上安装NDI4工具3.2 ENC1设备连接3.3 配置电脑的USB网卡的IP地址3.4 配置ENC1设备3.5 打开NDI工具的虚拟输入功能0 背景&#xff1a; HDMI视频采集卡分为内嵌式采集…
阅读更多...
【GCC编译优化系列】宏定义名称与函数同名是一种什么骚操作？

【GCC编译优化系列】宏定义名称与函数同名是一种什么骚操作？

作者简介 *架构师李肯&#xff08;全网同名&#xff09;**&#xff0c;一个专注于嵌入式IoT领域的架构师。有着近10年的嵌入式一线开发经验&#xff0c;深耕IoT领域多年&#xff0c;熟知IoT领域的业务发展&#xff0c;深度掌握IoT领域的相关技术栈&#xff0c;包括但不限于主流…
阅读更多...
​全网最牛的Fiddler系列文章(一)：fiddler的介绍及安装​

​全网最牛的Fiddler系列文章(一)：fiddler的介绍及安装​

Fiddler(1)&#xff1a;fiddler的介绍及安装 Fiddler简介 Fiddler是比较好用的web代理调试工具之一&#xff0c;它能记录并检查所有客户端与服务端的HTTP/HTTPS请求&#xff0c;能够设置断点&#xff0c;篡改及伪造Request/Response的数据&#xff0c;修改hosts&#xff0c;限…
阅读更多...
【UEFI实战】Redfish的BIOS实现1

【UEFI实战】Redfish的BIOS实现1

Redfish的BIOS实现 EDK2提供了Redfish框架&#xff0c;用来实现带外的BIOS配置&#xff0c;其基本框架如下&#xff1a; 通过RedfishPkg中提供的Driver&#xff0c;可以实现BIOS与BMC或者其它的软件进行通信。它主要分为两个部分&#xff0c;分别是Client和Foundation。Client…
阅读更多...
[论文解析]DREAMFUSION: TEXT-TO-3D USING 2D DIFFUSION

[论文解析]DREAMFUSION: TEXT-TO-3D USING 2D DIFFUSION

code links&#xff1a;dreamfusion3d.github.io 文章目录OverviewWhat problem is addressed in the paper?What is the key to the solution?What is the main contribution?What can we learn from ablation studies&#xff1f;Potential fundamental flaws; how this w…
阅读更多...
MATLB|基于粒子群算法的能源管理系统EMS（考虑光伏、储能 、柴油机系统）

MATLB|基于粒子群算法的能源管理系统EMS（考虑光伏、储能 、柴油机系统）

&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️❤️&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清…
阅读更多...
原子操作类之18罗汉增强

原子操作类之18罗汉增强

原子操作类之18罗汉增强 是什么 都是java.util.concurrent.atomic包下的 有红框圈起来的&#xff0c;也有蓝框圈起来的&#xff0c;为什么&#xff1f; 阿里巴巴Java开发手册 为什么说18罗汉增强&#xff0c;却只有16个 再分类 基本类型原子类 AtomicInteger AtomicBoolea…
阅读更多...
wpa_supplicant工具移植到嵌入式设备

wpa_supplicant工具移植到嵌入式设备

1、wpa_supplicant源码下载 (1)源码下载地址&#xff1a;http://w1.fi/releases/&#xff1b; (2)本文是以wpa_supplicant-2.6.tar.gz版本进行移植&#xff1b; 2、编译openssl 2.1、确定适配的openssl版本 Optional libraries for EAP-TLS, EAP-PEAP, and EAP-TTLS: - OpenS…
阅读更多...
【LeetCode】1827. 最少操作使数组递增

【LeetCode】1827. 最少操作使数组递增

题目描述 给你一个整数数组 nums &#xff08;下标从 0 开始&#xff09;。每一次操作中&#xff0c;你可以选择数组中一个元素&#xff0c;并将它增加 1 。 比方说&#xff0c;如果 nums [1,2,3] &#xff0c;你可以选择增加 nums[1] 得到 nums [1,3,3] 。 请你返回使 nums …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023