残差网络：经常使用的网络之一

1.随着神经网络的不断加深能改进精度吗？

不一定

①蓝色五角星表示最优值，Fi闭合区域表示函数，闭合区域的面积代表函数的复杂程度。在这个区域能够找到一个最优的模型（区域中的一个点表示，该点到最优值的距离衡量模型的好坏） 

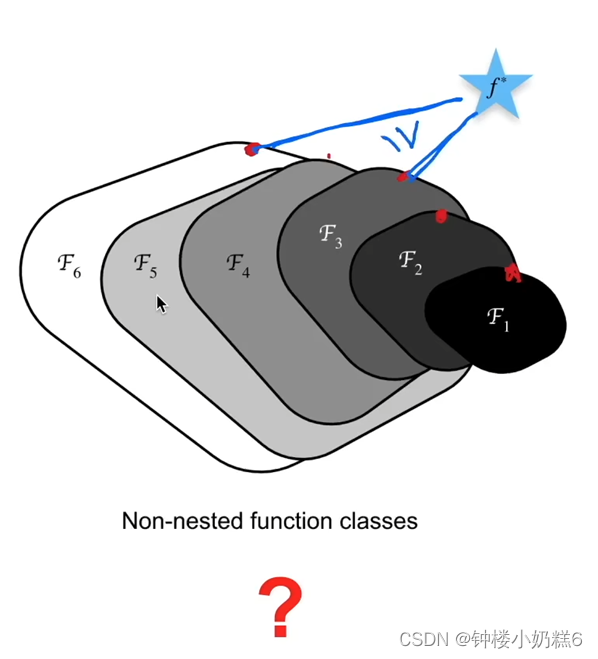
②随着函数的复杂度不断增加，函数的区域面积增大。逐渐偏离了原来的区域，并且在这个区域找的最优模型离最优值越来越远。非嵌套函数

③为了解决模型走偏的方法：每一次增加函数的复杂度的区域包含原来函数所在区域。嵌套函数，复杂的函数包含复杂度低的函数时，才能确保提高它的精度。

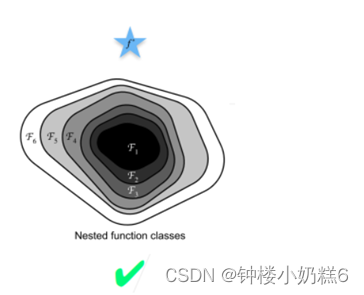
也就是说，增加函数的复杂度只会使函数在原有的面积基础上扩充，不会偏离原本存在的区域

④深度神经网络，新添加的层训练成恒等映射f(x)=x，新模型和原模型同样有效。新模型可能得出更优解来拟合训练数据集，添加层更容易降低训练误差。

2.残差网络的核心思想：每个附加层包含原始数据作为其元素之一。

3.残差块

 ①之前增加模型的深度是层层堆叠，残差网络的思想是堆叠层数的同时不会增加模型的复杂度

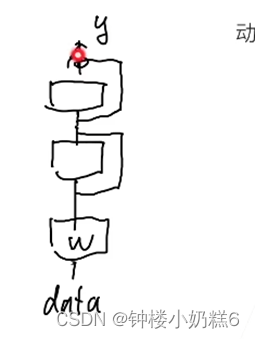
 ②x 是原始输入，f(x)是理想映射（激活函数的输入）

 ③正常块在虚线拟合出理想映射f(x),残差块虚线框拟合出残差映射f(x)-x

 ④残差映射要学习的恒等映射f(x)=x，将残差块虚线w和b设置为0

4.残差块的分类

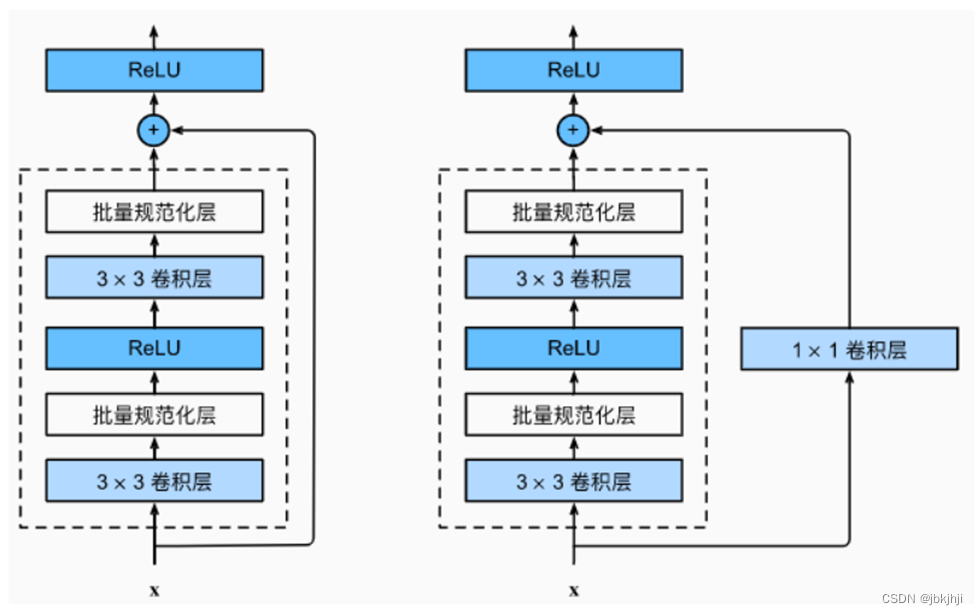
 ①左边的残差网络的第一种实现，直接将输入加在了叠加层输出上面

 ②右边的残差网络的第二种实现，包含了1*1的卷积，对输入进行了1*1的卷积变换了通道，再叠加再输出上面

 ③残差网络使用了VGG完整的3*3卷积设计

 ④残差块首先有2个相同输出通道的3*3卷积层，每个卷积层后跟着批量归一化和ReLu函数。通过跨层数据通路，跳过残差块，将输入直接加在最后ReLu激活函数前

 ⑤想要改变通道数，就需要引入额外的1*1卷积层来将输入变化成需要的形状再运算

5.ResNet的架构

 ①高宽减半的ResNet块。第一个卷积层的步幅为2，通过1*1卷积 通道数翻倍

 ②高宽不减半的ResNet块。重复多次，卷积层的步幅为1

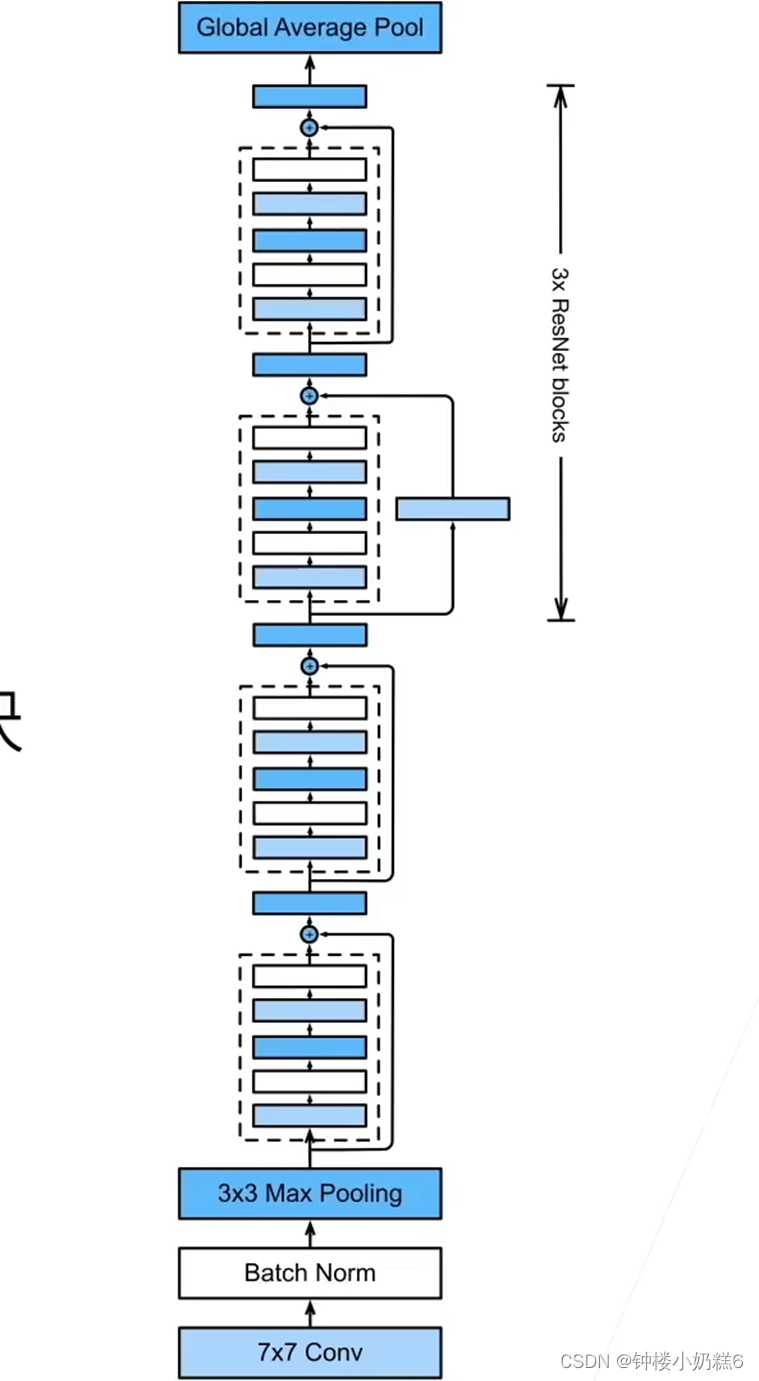
【总结】

①残差块使得很深的网络更容易训练（不管网络多深，有跨层数据通路连接的存在，使得始终能包含小的网络。跳转连接的存在，所以会将下层的小网络训练好再去训练更深的网络），甚至可以训练一千层网络（内存大，优化算法能够实现）

②残差网络对后来的深度神经网络设计产生了深远影响，无论是卷积网络还是全连接类网络，可以让网络更深。

③学习嵌套函数是神经网络的理想情况，在深层神经网络中，学习另一层作为恒等映射比较容易

④残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零

⑤利用残差块可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播

【总结2】ResNet为什么会训练出1000层的模型？

1.ResNet如何避免梯度消失?

将乘法运算变成加法运算

2. 假设有一个预测模型：y = f(x)

①x：输入

②f(x）：表示神经网络模型,如10个卷积层

③y：输出

W权重更新：（输出 y 中省略了损失函数）η：学习率

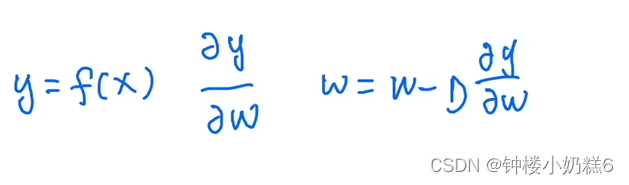
 y对w的梯度不能太小，如果太小的话，学习率无论多大都不起作用，并且影响数值的稳定性。

3. y‘ = g( f(x) ) 表示使用堆叠的方式对原有的模型进行加深

 

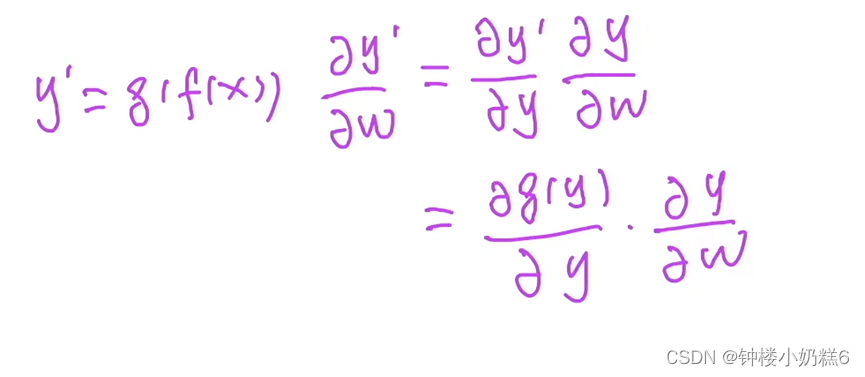
①比如加的是全连接层，全连接层拟合能力强，真实值和预测值的误差低，因此梯度也低。

假设所加的层的拟合能力比较强，第一项就会变得特别小，乘积的值就会变得特别小，也就是梯度就会变得特别小。

②就只能增大学习率，但可能增大也不是很有用，因为这是靠近底部数据层的更新，如果增加得太大，这样的话可能会导致数值不稳定

③如果中间有一项比较小的话，可能就会导致整个式子的乘积比较小，越到底层的话乘积就越小

4.残差网络：y‘' = f(x) + g( f(x) ) 表示使用残差连接的方式

 

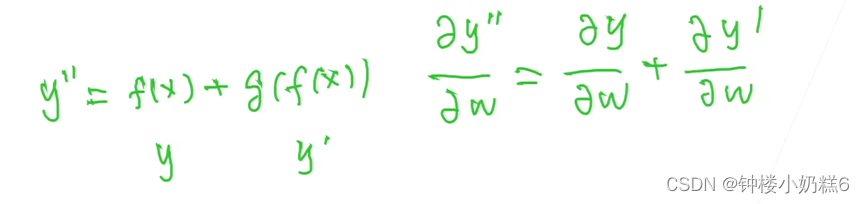
就算第二项的值比较小，但还是有第一项值进行补充。由于跨层数据通路的存在，模型底部的权重也能够获得比较大的梯度，进行更新。

5. 靠近数据端的权重 w 难以训练，但是由于加入了跨层数据通路，所以在计算梯度的时候，上层的loss可以通过跨层连接通路直接快速地传递给下层，所以在一开始，下面的层w也能够拿到比较大的梯度, 进行更新。

 

【代码实现】

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


# 残差块  输入通道数  输出通道数 是否使用1*1卷积 步幅
class Residual(nn.Module):  # @save
    def __init__(self, input_channels, num_channels, use_1x1conv=False, strides=1):
        super().__init__()
        # 有2个卷积层  第一个指定stride 第二个不指定
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:  # 使用1*1卷积
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))  # 1卷积层--批量规范---激活
        Y = self.bn2(self.conv2(Y))  # 2卷积层---批量规范层
        if self.conv3:  # 判断有没有1*1卷积
            X = self.conv3(X)
        Y += X
        return F.relu(Y)


# ResNet模型
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))


# 调用残差块 输入通道 输出通道 多少个残差块
def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk


b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1, 1)),
                    nn.Flatten(), nn.Linear(512, 10))


# 训练模型
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())