6260. 矩阵查询可获得的最大分数
难度困难7
给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。
找出一个大小为 k 的数组 answer ,且满足对于每个整数 queres[i] ,你从矩阵 左上角 单元格开始,重复以下过程:
- 如果
queries[i]严格 大于你当前所处位置单元格,如果该单元格是第一次访问,则获得 1 分,并且你可以移动到所有4个方向(上、下、左、右)上任一 相邻 单元格。 - 否则,你不能获得任何分,并且结束这一过程。
在过程结束后,answer[i] 是你可以获得的最大分数。注意,对于每个查询,你可以访问同一个单元格 多次 。
返回结果数组 answer 。
示例 1:
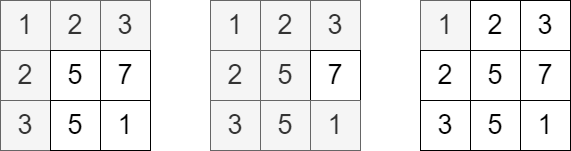
输入:grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
输出:[5,8,1]
解释:上图展示了每个查询中访问并获得分数的单元格。
示例 2:
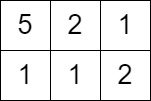
输入:grid = [[5,2,1],[1,1,2]], queries = [3]
输出:[0]
解释:无法获得分数,因为左上角单元格的值大于等于 3 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 105k == queries.length1 <= k <= 1041 <= grid[i][j], queries[i] <= 106
暴力模拟(超时)
class Solution {
int[][] dirt = {{0,1},{0,-1},{1,0},{-1,0}};
boolean[][] visited;
int n,m;
public int[] maxPoints(int[][] grid, int[] queries) {
n = grid.length;
m = grid[0].length;
int[] res = new int[queries.length];
for(int i = 0; i < res.length; i++){
if(grid[0][0] > queries[i]) continue;
visited = new boolean[n][m];
visited[0][0] = true;
res[i] = dfs(0,0,queries[i],grid);
}
return res;
}
public int dfs(int i, int j, int max, int[][] grid){
if(grid[i][j] >= max) return 0;
int res = 1;
for(int k = 0; k < dirt.length; k++){
int newx = i + dirt[k][0],newy = j + dirt[k][1];
if(newx >= 0 && newx < n && newy >= 0 && newy < m && !visited[newx][newy]){
visited[newx][newy] = true;
res += dfs(newx,newy,max,grid);
}
}
return res;
}
}
转化为海平面上升问题
https://leetcode.cn/problems/maximum-number-of-points-from-grid-queries/solution/by-liuliangcan-9osu/
- 题目的询问query实际上limit,即询问:对于limit从左上角开始,能floodfill到的格子个数。
- 再转换一下:左上角从虚空连接了高度limit的海平面,问能淹几个格子。
- 那么把询问离线排序,从小到大处理即可。
- 队列用小顶堆存,含义为:边界的格子最矮值先被淹。
- 于是只有堆顶小于limit时才需要继续搜索;否则等待海平面上升。
题解来自:0x3f : https://leetcode.cn/problems/maximum-number-of-points-from-grid-queries/solution/by-endlesscheng-qeei/
方法一:并查集
一看到这种具有大小关系的查询,直接就是经典的并查集加离线算法套路,力扣上有很多类似的题目,周赛双周赛就出现了好多次这样的!
把矩阵的元素值从小到大排序,询问也从小到大排序。
用双指针遍历矩阵元素值和询问,如果矩阵元素值小于询问值,就把该格子和周围四个格子中的小于询问值的格子相连。
用并查集可以实现相连的过程,同时维护每个连通块的大小。
答案就是左上角的连通块的大小(前提是左上角小于询问值)。
如果每次询问一次,dfs 一次,很可能超时,因此可以用并查集。离线处理,把边按权值排序,把问题按大小排序。然后离线的过程就是不断向图中加边的过程。
# 网格图
# 边是什么?边权是什么?
# 抽象成图
# 答案就是包含左上角的连通块的大小
# 连通块需要满足,点权 < q
# 点权处理起来比较麻烦,转换成边权就比较方便了,可以直接用并查集合并
# 怎么转换成边权?
# 把两个点连起来,需要满足什么条件?
# - 两个点的点权都是 < q
# 边权 = 两个点的点权的最大值
# 边权排序 询问排序
# 双指针遍历 边权 和 询问
# 每次把 < q 的边 所对应的两个点合并起来
# 答案 就是左上角(0)的连通块大小
python
class Solution:
def maxPoints(self, grid: List[List[int]], queries: List[int]) -> List[int]:
# 方法一:并查集
m,n = len(grid), len(grid[0])
mn = m*n
# 并查集模板
fa = list(range(mn))
size = [1] * mn # 自成一个大小为1的连通块
def find(x: int) -> int:
if fa[x] != x:
fa[x] = find(fa[x])
return fa[x]
def merge(f: int, to: int) -> None:
f = find(f)
to = find(to)
if f != to:
fa[f] = to
size[to] += size[f]
# 根据邻居关系进行建图处理
edges = []
for i, row in enumerate(grid):
for j,x in enumerate(row): # 对每个点只与其上面和左边建立边
if i > 0: # 建边(边权,当前点,上/左点)
edges.append((max(x,grid[i-1][j]),i*n+j,(i-1)*n+j)) # 当前点与上面点连边
if j > 0:
edges.append((max(x,grid[i][j-1]),i*n+j,i*n+j-1)) # 当前点与左边点连边
edges.sort(key=lambda p:p[0]) # 根据边权排序
ans = [0]*len(queries)
j = 0
# 按照查询值的大小排序,依次进行查询
for i,q in sorted(enumerate(queries), key = lambda p:p[1]): # 将queries值和下标合起来 根据值排序
# 根据查询值的大小利用指针持续更新并查集
while j < len(edges) and edges[j][0] < q:
merge(edges[j][1],edges[j][2])
j += 1
if grid[0][0] < q:
ans[i] = size[find(0)]
return ans
java
class Solution {
private static final int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private int[] fa, size;
public int[] maxPoints(int[][] grid, int[] queries) {
int m = grid.length, n = grid[0].length, mn = m * n;
// 并查集
fa = new int[mn];
for (var i = 0; i < mn; i++) fa[i] = i;
size = new int[mn];
Arrays.fill(size, 1);
// 矩阵元素从小到大排序,方便离线
var a = new int[mn][3];
for (var i = 0; i < m; ++i)
for (var j = 0; j < n; ++j)
a[i * n + j] = new int[]{grid[i][j], i, j};
Arrays.sort(a, (p, q) -> p[0] - q[0]);
// 查询的下标按照查询值从小到大排序,方便离线
var k = queries.length;
var id = IntStream.range(0, k).boxed().toArray(Integer[]::new);
Arrays.sort(id, (i, j) -> queries[i] - queries[j]);
var ans = new int[k];
var j = 0;
for (var i : id) {
var q = queries[i];
for (; j < mn && a[j][0] < q; ++j) {
int x = a[j][1], y = a[j][2];
// 枚举周围四个格子,值小于 q 才可以合并
for (var d : dirs) {
int x2 = x + d[0], y2 = y + d[1];
if (0 <= x2 && x2 < m && 0 <= y2 && y2 < n && grid[x2][y2] < q)
merge(x * n + y, x2 * n + y2); // 把坐标压缩成一维的编号
}
}
if (grid[0][0] < q)
ans[i] = size[find(0)]; // 左上角的连通块的大小
}
return ans;
}
// 并查集模板
private int find(int x) {
if (fa[x] != x) fa[x] = find(fa[x]);
return fa[x];
}
private void merge(int from, int to) {
from = find(from);
to = find(to);
if (from != to) {
fa[from] = to;
size[to] += size[from];
}
}
}
方法二:最小堆
仍然是离线询问,还可以从左上角出发向外搜索,用最小堆,初始把左上角的元素值及其坐标入堆。对每个询问,不断循环,如果堆顶元素值小于询问值,则弹出堆顶,继续搜索。
循环结束时,出堆的元素个数就是答案。
# 初始,把左上角和坐标(grid[0][0], 0, 0) 放到一个最小堆中
# 遍历排序后的询问,再套一个while循环
# 不断取堆顶,直到堆为空,或者 堆顶 >= q
# 循环内部:把这个位置向四种拓展,把拓展后的格子的值和坐标加到堆中
# 统计循环次数,或者 <q 的值的个数 cnt
# 循环结束之后,cnt 就是答案
python
class Solution:
def maxPoints(self, grid: List[List[int]], queries: List[int]) -> List[int]:
m,n = len(grid), len(grid[0])
ans = [0]*len(queries)
h = [(grid[0][0], 0, 0)] # 将左上角放到堆中
grid[0][0] = 0 # 表示访问过了
cnt = 0
# 按照查询值的大小排序,依次进行查询
for qi,q in sorted(enumerate(queries), key = lambda p:p[1]):
# 不断取堆顶,直到堆为空,或者 堆顶 >= q
while h and h[0][0] < q:
cnt += 1
val, i, j = heappop(h)
# 遍历结点四周
for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):
if 0<=x<m and 0<=y<n and grid[x][y]: # 合法且未访问
heappush(h, (grid[x][y], x, y))
grid[x][y] = 0
ans[qi] = cnt
return ans
java
class Solution {
private static final int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int[] maxPoints(int[][] grid, int[] queries) {
// 查询的下标按照查询值从小到大排序,方便离线
var k = queries.length;
var id = IntStream.range(0, k).boxed().toArray(Integer[]::new);
Arrays.sort(id, (i, j) -> queries[i] - queries[j]);
var ans = new int[k];
var pq = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);
pq.add(new int[]{grid[0][0], 0, 0});
grid[0][0] = 0; // 充当 vis 数组的作用
int m = grid.length, n = grid[0].length, cnt = 0;
for (var i : id) {
var q = queries[i];
while (!pq.isEmpty() && pq.peek()[0] < q) {
++cnt;
var p = pq.poll();
for (var d : dirs) { // 枚举周围四个格子
int x = p[1] + d[0], y = p[2] + d[1];
if (0 <= x && x < m && 0 <= y && y < n && grid[x][y] > 0) {
pq.add(new int[]{grid[x][y], x, y});
grid[x][y] = 0; // 充当 vis 数组的作用
}
}
}
ans[i] = cnt;
}
return ans;
}
}
相关题目
1697. 检查边长度限制的路径是否存在
在线算法:
- 在线算法就是边输入边处理,不一定要等所有输入都完成以后才会给出相应的解答。
离线算法:
- 在问题的一开始就要知道所有的数据,然后才能输出结果。