参考线平滑理论
决策规划流程第一步是参考线的生成,然后将障碍物进行投影到以参考线为坐标轴的frenet坐标系。参考线是很关键的一部,解决了导航路径过长,不平滑,不利于坐标转换找匹配点的问题。利用参考线,每一个规划周期,找到车在导航路径投影点,以投影点为坐标原点,往后取30米,往前取150米范围内的点,做平滑处理,平滑以后的点就是参考线。在Carla仿真器中,全局规划得到的航路点,可以以匹配点为原点,往后取10个点,往前取40个点。再对这些点进行平滑处理。
参考线平滑算法,采样了二次规划,主要定义以下损失值:
- 平滑度
- 长度要均匀紧凑
- 几何相似代价
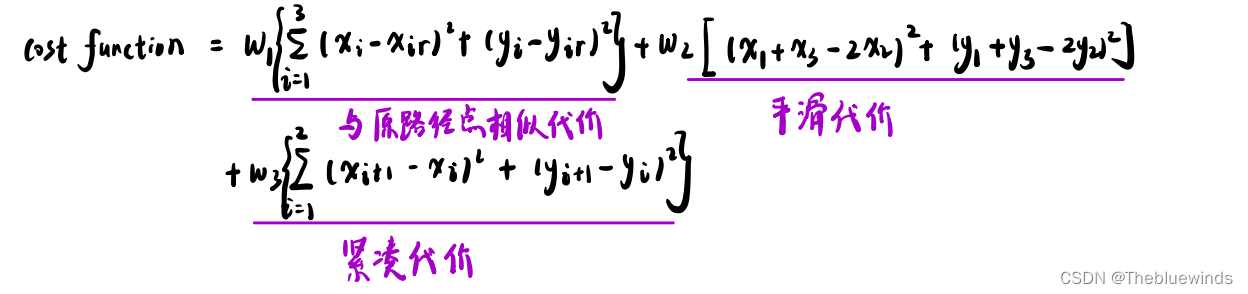
将问题转化为二次规划问题,使得损失函数最小:
1
2
x
T
H
x
+
f
T
x
=
min
s
.
t
A
x
⩽
b
l
b
⩽
x
⩽
u
b
\frac{1}{2}x^THx\,\,+\,\,f^Tx=\min \\ s.t\,\, Ax\,\,\leqslant b \\ lb\,\,\leqslant x\leqslant ub
21xTHx+fTx=mins.tAx⩽blb⩽x⩽ub
下面通过损失函数来进行推导。
平滑代价:
(
x
1
+
x
3
−
2
x
2
)
2
+
(
y
1
+
y
3
−
2
y
2
)
2
=
(
x
1
+
x
3
−
2
x
2
,
y
1
+
y
3
−
2
y
2
)
(
x
1
+
x
3
−
2
x
2
,
y
1
+
y
3
−
2
y
2
)
T
\left( x_1+x_3-2x_2 \right) ^2\,\,+\,\,\left( y_1+y_3-2y_2 \right) ^2 \\ =\,\,\left( x_1\,\,+\,\,x_3\,\,-2x_2, y_1+y_3-2y_2 \right) \left( x_1+x_3-2x_2, y_1+y_3-2y_2 \right) ^T
(x1+x3−2x2)2+(y1+y3−2y2)2=(x1+x3−2x2,y1+y3−2y2)(x1+x3−2x2,y1+y3−2y2)T
其中有:
(
x
1
+
x
3
−
2
x
2
,
y
1
+
y
3
−
2
y
2
)
=
(
x
1
,
y
1
,
x
2
,
y
2
,
x
3
,
y
3
)
(
1
0
0
1
−
2
0
0
−
2
1
0
0
1
)
\left( x_1\,\,+\,\,x_3\,\,-2x_2, y_1+y_3-2y_2 \right) \,\,=\,\,\left( x_1, y_1, x_2, y_2, x_3, y_3 \right) \left( \begin{array}{c} \begin{array}{c} \begin{array}{c} \begin{matrix} 1& 0\\ \end{matrix}\\ \begin{matrix} 0& 1\\ \end{matrix}\\ \begin{matrix} -2& 0\\ \end{matrix}\\ \begin{matrix} 0& -2\\ \end{matrix}\\ \end{array}\\ \begin{matrix} 1& 0\\ \end{matrix}\\ \end{array}\\ \begin{matrix} 0& 1\\ \end{matrix}\\ \end{array} \right)
(x1+x3−2x2,y1+y3−2y2)=(x1,y1,x2,y2,x3,y3)
1001−200−21001
将
(
x
1
,
y
1
,
x
2
,
y
2
,
x
3
,
y
3
)
\left( x_1, y_1, x_2, y_2, x_3, y_3 \right)
(x1,y1,x2,y2,x3,y3)记作x,系数矩阵记作
A
1
A_1
A1, 然后可以得到:
(
x
1
+
x
3
−
2
x
2
)
2
+
(
y
1
+
y
3
−
2
y
2
)
2
=
x
T
A
1
T
A
1
x
\left( x_1+x_3-2x_2 \right) ^2+\left( y_1+y_3-2y_2 \right) ^2\,\,=\,\,x^TA_{1}^{T}A_1x
(x1+x3−2x2)2+(y1+y3−2y2)2=xTA1TA1x
对于n个点的情况为:
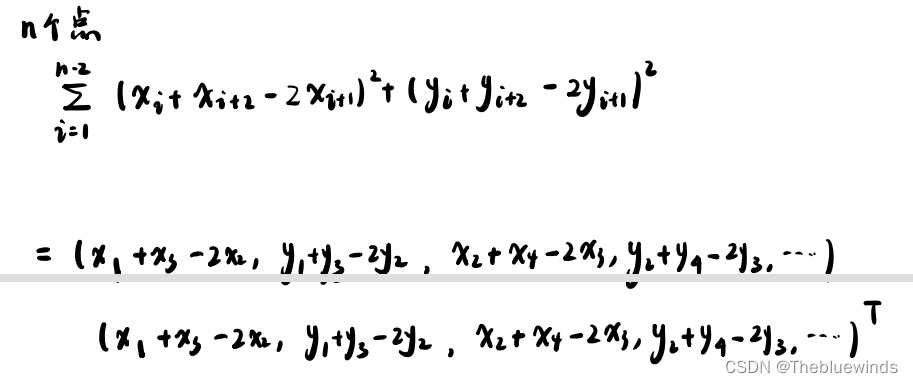
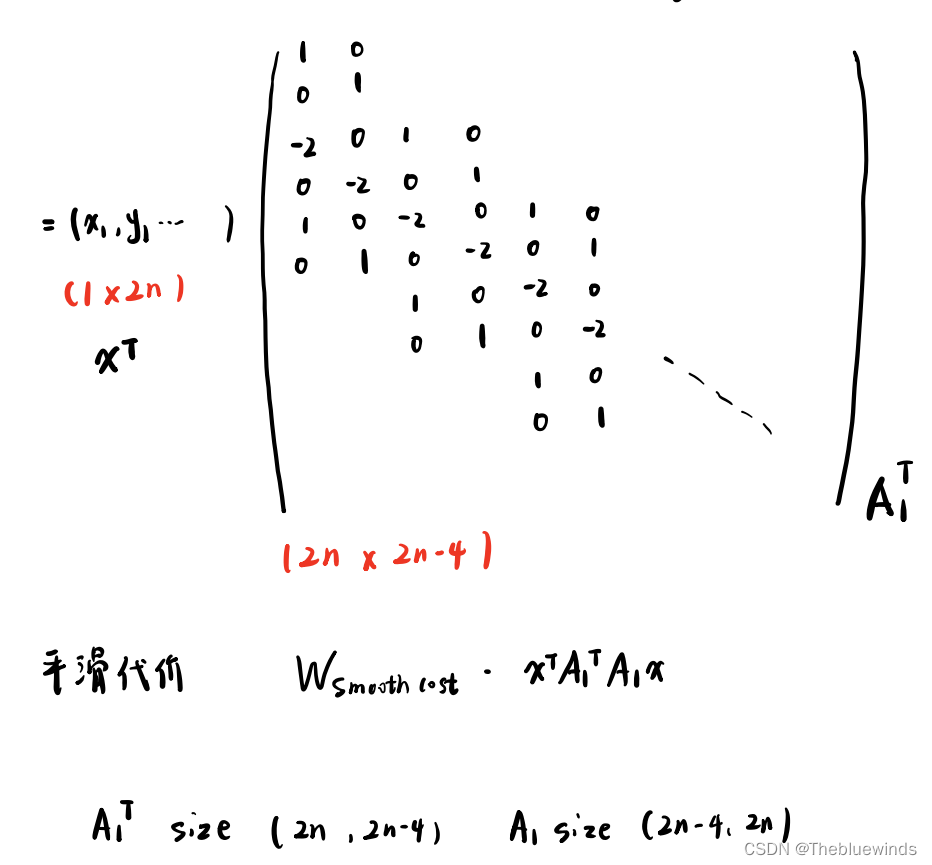
紧凑代价:
同理可以推出紧凑型代价,建议用手写一篇加深印象。

几何相似性代价:

综上可得,统一得向量表达的代价函数为:
cos
t
f
u
n
c
t
i
o
n
=
x
T
(
W
s
m
o
o
t
h
⋅
A
1
T
A
1
+
W
l
e
n
g
t
h
A
2
T
A
2
+
W
r
e
f
A
3
T
A
3
)
x
T
+
W
r
e
f
⋅
h
T
x
\cos t\,\,function\,\,=\,\,x^T\left( W_{smooth}\cdot A_{1}^{T}A_1\,\,+\,\,W_{length}A_{2}^{T}A_2+W_{ref}A_{3}^{T}A_3 \right) x^T\,\,+\,\,W_{ref}\cdot h^Tx
costfunction=xT(Wsmooth⋅A1TA1+WlengthA2TA2+WrefA3TA3)xT+Wref⋅hTx
注意h是表示参考点的列向量。
对比二次规划的模板:
公式
1
2
x
T
H
x
+
f
T
x
=
min
s
.
t
A
x
⩽
b
l
b
⩽
x
⩽
u
b
\frac{1}{2}x^THx\,\,+\,\,f^Tx=\min \\s.t\,\, Ax\,\,\leqslant b\\lb\,\,\leqslant x\leqslant ub
21xTHx+fTx=mins.tAx⩽blb⩽x⩽ub
可以有:
H
=
2
(
W
s
m
o
o
t
h
⋅
A
1
T
A
1
+
W
l
e
n
g
t
h
A
2
T
A
2
+
W
r
e
f
A
3
T
A
3
)
H\,\,=\,\,2\left( W_{smooth}\cdot A_{1}^{T}A_1\,\,+\,\,W_{length}A_{2}^{T}A_2+W_{ref}A_{3}^{T}A_3 \right)
H=2(Wsmooth⋅A1TA1+WlengthA2TA2+WrefA3TA3)
然后:
f
T
=
W
r
e
f
⋅
h
T
f^T\,\,=\,\,W_{ref}\cdot h^T
fT=Wref⋅hT。
约束就是向量x的约束:
x
=
(
x
1
,
y
1
,
⋯
,
x
n
,
y
n
)
T
x
r
e
f
=
(
x
1
r
,
y
1
r
,
⋯
,
x
n
r
,
y
n
r
)
x\,\,=\,\,\left( x_1, y_1, \cdots , x_n, y_n \right) ^T \\ x_{ref}\,\,=\,\, \left( x_{1r}, y_{1r}, \cdots , x_{nr}, y_{nr} \right)
x=(x1,y1,⋯,xn,yn)Txref=(x1r,y1r,⋯,xnr,ynr)
这两者不能够差距太远,因此要求:
∣
x
−
x
r
e
f
∣
⩽
b
u
f
f
\left| x\,\,-\,\,x_{ref} \right|\leqslant buff\,\,
∣x−xref∣⩽buff
总结一下步骤:
- 构建x向量。
- 构建 A 1 A_1 A1矩阵 A 2 A_2 A2和 A 3 A_3 A3矩阵,其中A1代表平滑代价,大小为(2n-4, 2n)。A2代表紧凑代价,大小为(2n-2, 2n)。A3表示几何相似代价,是一个单位矩阵,大小为(2n, 2n)
- 计算 H = 2 ( W s m o o t h ⋅ A 1 T A 1 + W l e n g t h A 2 T A 2 + W r e f A 3 T A 3 ) H\,\,=\,\,2\left( W_{smooth}\cdot A_{1}^{T}A_1\,\,+\,\,W_{length}A_{2}^{T}A_2+W_{ref}A_{3}^{T}A_3 \right) H=2(Wsmooth⋅A1TA1+WlengthA2TA2+WrefA3TA3)
- 根据参考点计算: f T = W r e f ⋅ h T f^T\,\,=\,\,W_{ref}\cdot h^T fT=Wref⋅hT
- 二次规划求解。
下面逐一对上述步骤进行代码分析。
参考线理论代码实践
1、构建x向量
"""
local_frenet_path_xy: 可以是[(x_ref0, y_ref0), (x_ref1, y_ref1), ...],
也可以是[(x_ref0, y_ref0,theta0, kappa0), (x_ref1, y_ref1, theta1, kappa1), ...],
"""
n = len(local_frenet_path_xy) # 待平滑的点。
# 需要构成x向量为(x1,y1, x2,y2,....xn,yn)的参考点。
x_ref = np.zeros(shape=(2 * n, 1)) # 【x_ref0, y_ref0, x_ref1, y_ref1, ...]' 输入坐标构成的坐标矩阵, (2*n, 1)
lb = np.zeros(shape=(2 * n, 1)) # low bound 下边界
ub = np.zeros(shape=(2 * n, 1)) # up bound 上边界
for i in range(n):
x_ref[2 * i] = local_frenet_path_xy[i][0]
x_ref[2 * i + 1] = local_frenet_path_xy[i][1]
# 确定上下边界
# 平滑后点移动不能超过x_thre的范围。
lb[2 * i] = local_frenet_path_xy[i][0] - x_thre
lb[2 * i + 1] = local_frenet_path_xy[i][1] - y_thre
ub[2 * i] = local_frenet_path_xy[i][0] + x_thre
ub[2 * i + 1] = local_frenet_path_xy[i][1] + y_thre
2、构建三个A矩阵。
A1 = np.zeros(shape=(2 * n - 4, 2 * n))
for i in range(n - 2):
A1[2 * i][2 * i + 0] = 1
# A1[2 * i][2 * i + 1] = 0
A1[2 * i][2 * i + 2] = -2
# A1[2 * i][2 * i + 3] = 0
A1[2 * i][2 * i + 4] = 1
# A1[2 * i][2 * i + 5] = 0
# A1[2 * i + 1][2 * i + 0] = 0
A1[2 * i + 1][2 * i + 1] = 1
# A1[2 * i + 1][2 * i + 2] = 0
A1[2 * i + 1][2 * i + 3] = -2
# A1[2 * i + 1][2 * i + 4] = 0
A1[2 * i + 1][2 * i + 5] = 1
A2 = np.zeros(shape=(2 * n - 2, 2 * n))
for i in range(n - 1):
A2[2 * i][2 * i + 0] = 1
# A2[2 * i][2 * i + 1] = 0
A2[2 * i][2 * i + 2] = -1
# A2[2 * i][2 * i + 3] = 0
# A2[2 * i + 1][2 * i + 0] = 0
A2[2 * i + 1][2 * i + 1] = 1
# A2[2 * i + 1][2 * i + 2] = 0
A2[2 * i + 1][2 * i + 3] = -1
A3 = np.identity(2 * n)
3、计算H矩阵
H = 2 * (w_cost_smooth * np.dot(A1.transpose(), A1) +
w_cost_length * np.dot(A2.transpose(), A2) +
w_cost_ref * A3)
4、计算f
f = -2 * w_cost_ref * x_ref
5、二次规划求解
在进行二次规划求解之前有必要先了解一下Python中的QP求解器。
minimize 1 2 x T P x + q T x subject to G x ≤ h A x = b \begin{align*} \text{minimize} \ &\frac{1}{2} x^T P x + q^T x \\ \text{subject to} \ & G x \leq h \\ & A x = b \end{align*} minimize subject to 21xTPx+qTxGx≤hAx=b
上面这个函数为二次规划QP问题的标准格式,最上面的公式为最小化目标函数,P是一个对称矩阵,代表二次项系数,q是列向量,表示线性项系数。 x是列向量,表示的是优化问题的变量,也就是求解的目标。
subject to 对应的是等式约束和不等式约束,其中G表示不等式约束的系数矩阵,h为不等式约束右边值。A代表等式约束系数。b是一个列向量,表示等式约束的右边值。
在python中可以采用cvxopt来对这个二次规划问题进行求解,它通过内部的优化算法来找到问题的最优解。参数说明:
P:二次项矩阵,是一个n x n的对称矩阵。q:线性项矩阵,是一个长度为n的列向量。G:不等式约束的系数矩阵,是一个m x n的矩阵。h:不等式约束的右边值,是一个长度为m的列向量。A:等式约束的系数矩阵,是一个p x n的矩阵。b:等式约束的右边值,是一个长度为p的列向量。
求解以后的返回值为一个字典类型,其中包括以下内容:
'x':最优解的列向量。'primal objective':优化后的目标函数值。'dual objective':对偶问题的目标函数值。'status':优化求解的状态,例如’optimal’表示求解成功。
下面举例说明通过cvxopt求解的一个简单过程:
import numpy as np
import cvxopt
# 定义二次规划问题的矩阵
P = np.array([[1.0, 0.5], [0.5, 1.0]])
q = np.array([-2.0, -3.0])
G = np.array([[-1.0, 0.0], [0.0, -1.0]])
h = np.array([0.0, 0.0])
A = np.array([[1.0, 1.0]])
b = np.array([1.0])
# 求解二次规划问题
res = cvxopt.solvers.qp(cvxopt.matrix(P), cvxopt.matrix(q), cvxopt.matrix(G), cvxopt.matrix(h), cvxopt.matrix(A), cvxopt.matrix(b))
# 提取优化结果
optimal_solution = np.array(res['x'])
print("Optimal Solution:")
print(optimal_solution)
print("Optimal Objective Value:")
print(res['primal objective'])
接下来回到Carla代码中参考线平滑的求解过程,已经求得了H系数,和f系数。其次还有不等式约束:
∣
x
−
x
r
e
f
∣
⩽
b
u
f
f
\left| x\,\,-\,\,x_{ref} \right|\leqslant buff\,\,
∣x−xref∣⩽buff
接下来构造cvxopt求解器的系数,由于目标函数已经构建出来了,其中H就是G,f就是q。因此只需要把不等式约束的系数构建好就可以求解了。
G = np.concatenate((np.identity(2 * n), -np.identity(2 * n))) # (4n, 2n) identity创建2n*2n的单位矩阵。
h = np.concatenate((ub, -lb)) # (4n, 1)
解释以下,这里的G和h,因为有上界和下界约束,也就是有两个不等式约束条件。需要将G和h构造成为矩阵形式。
G
=
[
I
2
n
−
I
2
n
]
h
=
[
u
b
−
l
b
]
G=\left[ \begin{array}{c} I_{2n}\\ -I_{2n}\\ \end{array} \right] \\ h\,\,=\,\,\left[ \begin{array}{c} ub\\ -lb\\ \end{array} \right]
G=[I2n−I2n]h=[ub−lb]
其中ub和lb如下:
u
b
=
[
x
1
+
b
u
f
f
y
1
+
b
u
f
f
⋮
⋮
x
n
+
b
u
f
f
y
n
+
b
u
f
f
]
l
b
=
[
x
1
−
b
u
f
f
y
1
−
b
u
f
f
⋮
⋮
x
n
−
b
u
f
f
y
n
−
b
u
f
f
]
ub\,\,=\,\,\left[ \begin{array}{c} x_1+buff\\ y_1+buff\\ \vdots\\ \vdots\\ x_n+buff\\ y_n+buff\\ \end{array} \right] \,\, lb\,\,=\,\,\left[ \begin{array}{c} x_1-buff\\ y_1-buff\\ \vdots\\ \vdots\\ x_n-buff\\ y_n-buff\\ \end{array} \right]
ub=
x1+buffy1+buff⋮⋮xn+buffyn+buff
lb=
x1−buffy1−buff⋮⋮xn−buffyn−buff
接下来就可以对二次规划求解了:
cvxopt.solvers.options['show_progress'] = False # 程序没有问题之后不再输出中间过程
# 计算时要将输入转化为cvxopt.matrix
# 该方法返回值是一个字典类型,包含了很多的参数,其中x关键字对应的是优化后的解
res = cvxopt.solvers.qp(cvxopt.matrix(H), cvxopt.matrix(f), G=cvxopt.matrix(G), h=cvxopt.matrix(h))
因为得到的x还是$\left( x_{1,}y_1, \cdots x_n,y_n \right) $的格式,因此还要进行一定的改造。将其变成:包含点坐标的列表 [(x1, y1), (x2, y2), ...]
local_path_xy_opt = []
for i in range(0, len(res['x']), 2):
local_path_xy_opt.append((res['x'][i], res['x'][i + 1]))
还需要计算平滑后的坐标点的航向角和曲率:
theta_list, k_list = cal_heading_kappa(local_path_xy_opt) # 计算坐标点的航向角和曲率。
x_y_theta_kappa_list = []
for i in range(len(local_path_xy_opt)):
x_y_theta_kappa_list.append(local_path_xy_opt[i] + (theta_list[i], k_list[i]))
return x_y_theta_kappa_list
计算航向角和曲率的方法在LQR的章节中有描述,主要利用中点欧拉法来实现。
这样就完成了对参考线轨迹点的平滑处理。



![[语义分割] DeepLab v2(膨胀卷积、空洞卷积、多尺度信息融合、MSc、ASPP、空洞空间金字塔池化、Step学习率策略、Poly学习率策略)](https://img-blog.csdnimg.cn/526f8d16f5c344dabafa2cb105b7a905.png#pic_center)